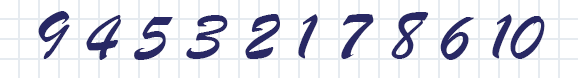May s'est avéré froid, le chauffage a été désactivé et les puissances de calcul (et de chauffage) étaient nulles, mais elles étaient inactives. Alors pourquoi ne pas les charger de quelque chose d' inutile , qui réchauffera et divertira.Mais je vais partir de loin. L'autre jour, j'ai rencontré un problème pour un lycée avec la formulation suivante: «Plusieurs entiers positifs consécutifs ont été écrits de manière à ce que la somme de tous les trois nombres consécutifs soit divisible entièrement par le nombre le plus à gauche de ce triple. "Quel est le nombre maximum de chiffres qui pourraient être écrits si le dernier numéro de ligne est impair?"Avec cette restriction, il est facile de prouver que dans chaque triple de nombres impairs, il y aura plus que des nombres pairs. Et comme la différence entre eux ne peut pas être supérieure à un, la longueur maximale de la séquence est limitée à cinq chiffres. Et à titre d'exemple, nous pouvons donner la séquence 4 5 3 2 1 .Une preuve détaillée peut être trouvée ici.Mais que se passe-t-il si nous supprimons la restriction indiquée sur la bizarrerie du dernier numéro? Ensuite, à droite, vous pouvez ajouter les chiffres 7 6 8 , en étendant la séquence à huit chiffres. Vous pouvez également ajouter une douzaine et attacher les neuf manquants à gauche. Eh bien, et ce ne sera probablement pas la seule et non la plus longue permutation.En fait, essayant de raisonner logiquement, je n'ai trouvé aucune preuve des limites de telles séquences et j'ai décidé d'impliquer une calculatrice dans le radiateur domestique pour analyse . Recherche grossière et exhaustive de tous les N ! les options ont rapidement montré l'échec de la méthode, mais l'énumération directionnelle a permis des progrès significatifs, et le résultat était à la fois attendu et inattendu.Il s'est avéré que pour tous les N jusqu'à 29 inclus, de telles permutations des nombres de 1 à N se trouvent en effet cependant pour les longueurs 27 et 29 dans une seule variante. Mais il y a ensuite des lacunes. Pour les permutations de tailles 30, 31, 32 et 33, il n'y a pas de solution; pour le nombre 34, il y en a une.tel33 23 10 13 7 6 1 29 27 2 25 21 4 17 15 19 11 8 3 5 31 9 22 14 30 26 34 18 16 20 12 28 32 24
Là encore, deux espaces. Pour les valeurs 37 et 38, ces séquences ne sont pas uniques, puis un échec. J'étais même désespéré, les dix suivants se sont avérés être complètement vides, mais la chance a souri, pour N = 51 la permutation nécessaire est toujours trouvée.elle est là46 45 1 44 49 39 10 29 21 37 5 32 23 41 51 31 20 11 9 2 43 35 8 27 13 14 25 3 47 40 7 33 16 17 15 19 26 50 28 22 6 38 34 4 30 18 42 48 36 12 24
Il y en a même deux, mais ils se croisent pour la plupart.De plus, le vide est à nouveau prévu, au moins pour les numéros 52 et 53 il n'y a pas de solutions, mais je n'ai pas cherché plus loin. Néanmoins, à chaque étape, le temps d'attente augmente de façon exponentielle, et la maison est déjà devenue beaucoup plus chaude, j'ai décidé de m'arrêter là pour l'instant.Si vous réduisez le nombre d'options possibles trouvées dans un tableau, vous pouvez créer le graphique suivant.
Eh bien, oui, il y a quelque chose à méditer.Dans le problème d'origine, il n'était pas nécessaire de démarrer la série naturelle à partir d'une seule. L'essentiel est que tous les nombres de a à b se trouvent dans la séquence. Mais j'ai essayé, ça ne fait qu'empirer, il y a encore moins d'options. Ce qui, en fait, est explicable. Plus le nombre est à gauche du triple, plus la multiplicité peut être faible par la somme des deux autres, c'est-à-dire le moins d'options disponibles. Eh bien, la question de la limite supérieure des longueurs de telles séquences reste ouverte. Avec la croissance de la dimensionnalité, la probabilité de succès est clairement réduite, mais est-elle annulée? Ou plus loin, ils rencontreront, bien que rarement, de telles permutations (in) intéressantes.Enfin, vous pouvez peut-être apporter le code du programme de chauffage,vrai qu'il est sur Haskellimport Data.List (delete)
import Control.Parallel.Strategies
import System.Environment
pvc :: Int -> Int -> [Int] -> [[Int]]
pvc a b [] = [[a,b]]
pvc a b xs = [a:ys |
x <- xs,
mod (a + b + x) a == 0,
ys <- pvc b x (delete x xs)]
gen :: Int -> [[[Int]]]
gen n =
let ab = [(a, b) | a <- [1..n], b <- delete a [1..n]]
in map hlp ab `using` parList rseq
where
hlp (a,b) = pvc a b $ delete a $ delete b [1..n]
main = do
[n] <- getArgs
print $ concat $ gen $ read n