Bonjour, Habr! Aujourd'hui, je veux partager un petit exemple de la façon d'effectuer une analyse de cluster. Dans cet exemple, le lecteur ne trouvera pas de réseaux de neurones et d'autres directions à la mode. Cet exemple peut servir de point de référence afin de faire une analyse de cluster petite et complète pour d'autres données. Toute personne intéressée - bienvenue au chat.
Faites immédiatement une réserve, cet article ne prétend en aucun cas être académique dans son intégralité, unicité des résultats obtenus, ou exhaustivité de la couverture de la question. L'article est destiné à démontrer les étapes de base de l'analyse de cluster classique, qui peuvent être utilisées pour une étude simple et significative (précédant éventuellement une étude plus détaillée). Toutes corrections, commentaires et ajouts sur le fond sont les bienvenus.
Les données sont un échantillon de la consommation d'alcool par pays par habitant et par type de boissons alcoolisées (bière, vin, spiritueux, etc.) pour 2010 en pourcentage de la consommation d'alcool par habitant. Les données contiennent également: la consommation quotidienne moyenne d'alcool par habitant en grammes d'alcool pur et toute la consommation d'alcool (enregistrée + non comptabilisée) par habitant (uniquement les buveurs en litres d'alcool pur).
Dans le même temps, chaque pays appartient conditionnellement à l'un des groupes géographiques: est, centre et ouest. La division est très arbitraire et très controversée pour diverses raisons, mais nous partirons de ce que nous avons. Source de données - Rapport de situation sur l'alcool et la santé dans le monde 2014, S. 289-364
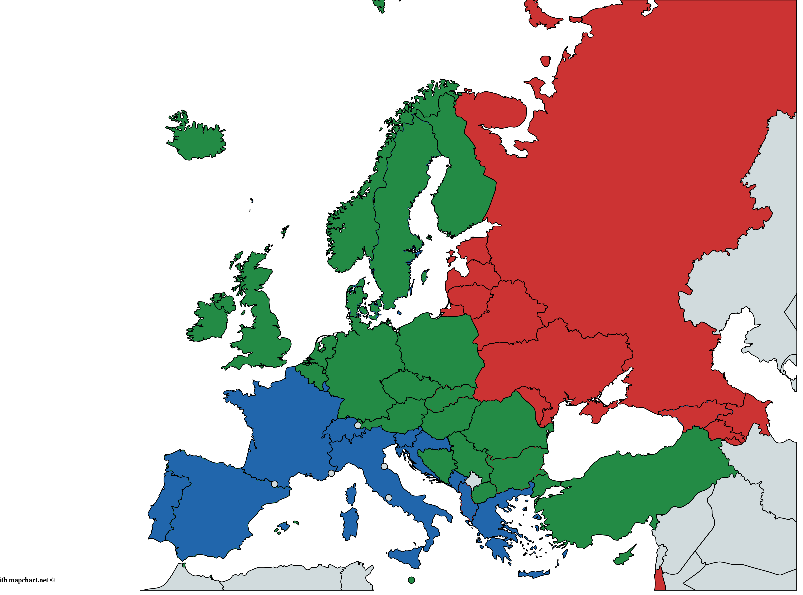
(Peint à la main, il peut y avoir des erreurs, mais l'idée générale, je pense, est compréhensible)
Analyse préliminaire
Connectez les bibliothèques utilisées.
library(rgl)
library(heplots)
library(MVN)
library(klaR)
library('Morpho')
library(caret)
library(mclust)
library(ggplot2)
library(GGally)
library(plyr)
library(psych)
library(GPArotation)
library(ggpubr)
, .
#
data <- read.table("alcohol_data.csv", header=TRUE, sep=",")
#
rownames(data) <- make.names(data[,1], unique = TRUE)
# ,
data <- data[,-1]
data <- na.omit(data)
#
head(data)
summary(data)
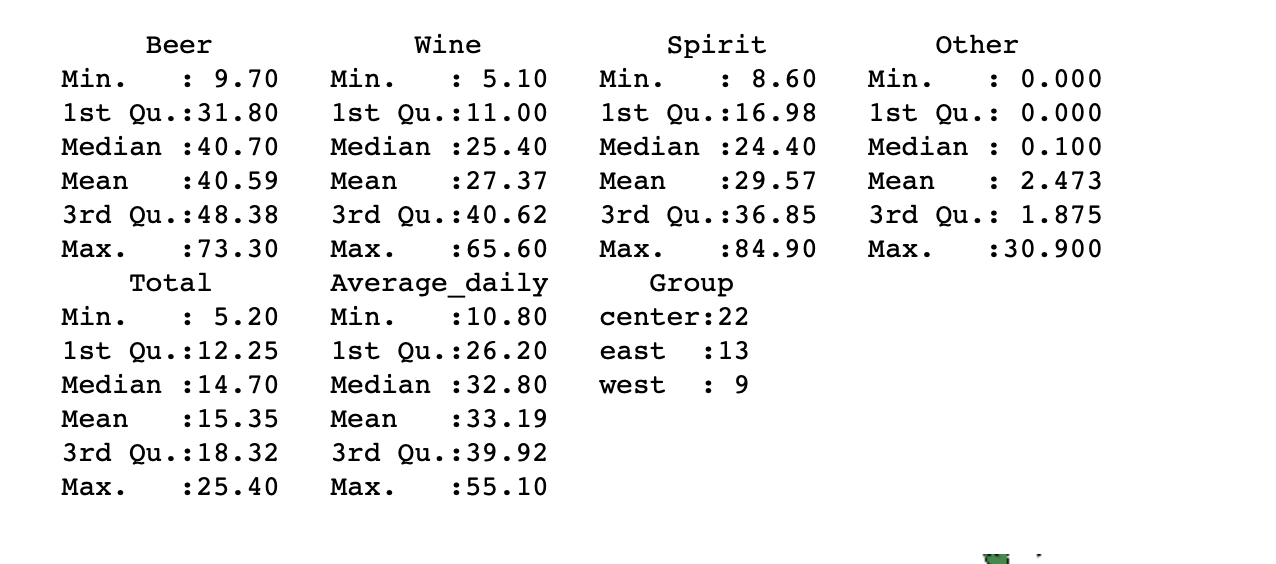
, . , Other , , , , . , , , , . , . - .
, , , .
options(rgl.useNULL=TRUE)
open3d()
mfrow3d(2,2)
levelColors <- c('west'='blue', 'east'='red', 'center'='yellow')
plot3d(data$Beer, data$Wine, data$Spirit, xlab="Beer", ylab="Wine", zlab="Spirit", col = levelColors[data$Group], size=3)
widget <- rglwidget()
widget
, . , .
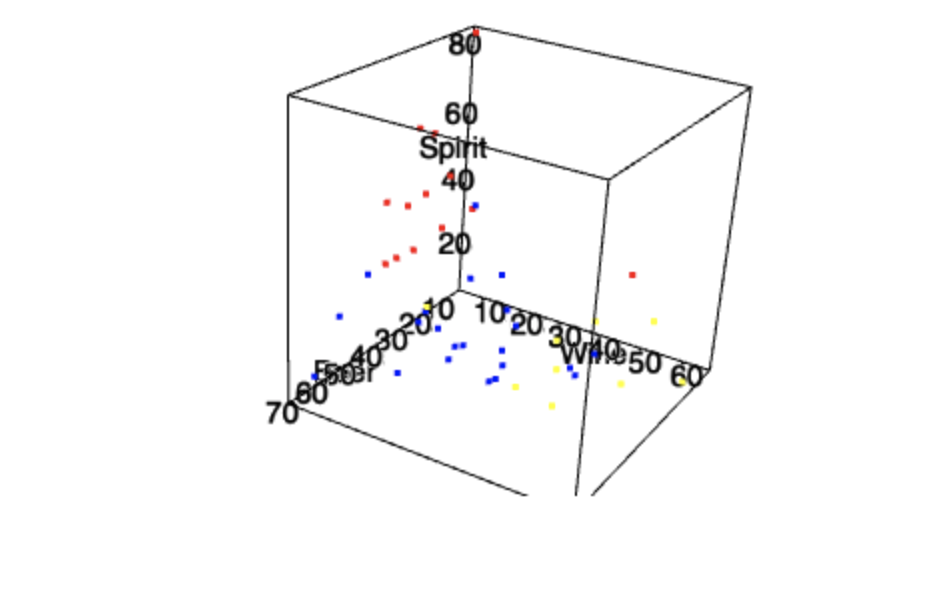
ggpairs(
data,
mapping = ggplot2::aes(color = data$Group),
upper = list(continuous = wrap("cor", alpha = 0.5), combo = "box"),
lower = list(continuous = wrap("points", alpha = 0.3), combo = wrap("dot", alpha = 0.4)),
diag = list(continuous = wrap("densityDiag",alpha = 0.5)),
title = "Alcohol"
)
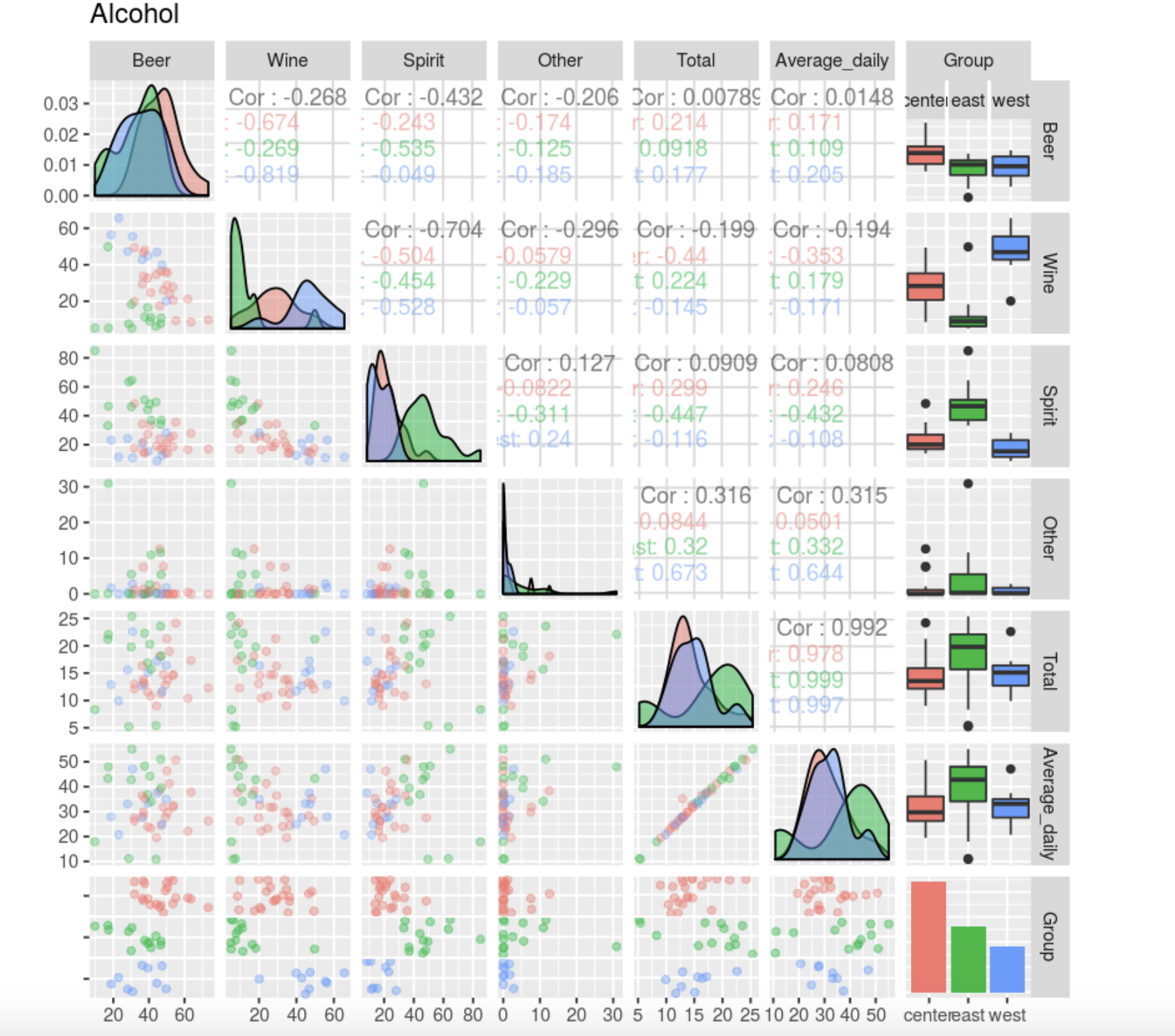
Average Total , Average.
data <- data[, -6]
, , , , . .
data[data$Wine>60,]
, , , , - , , .
data[data$Spirit>70,]
data[data$Spirit<10,]
, , .
,
split(data[,1:5],data$Group)
$center
$east
$west
ggpairs(
data,
mapping = ggplot2::aes(color = data$Group),
diag=list(continuous="bar", alpha=0.4)
)
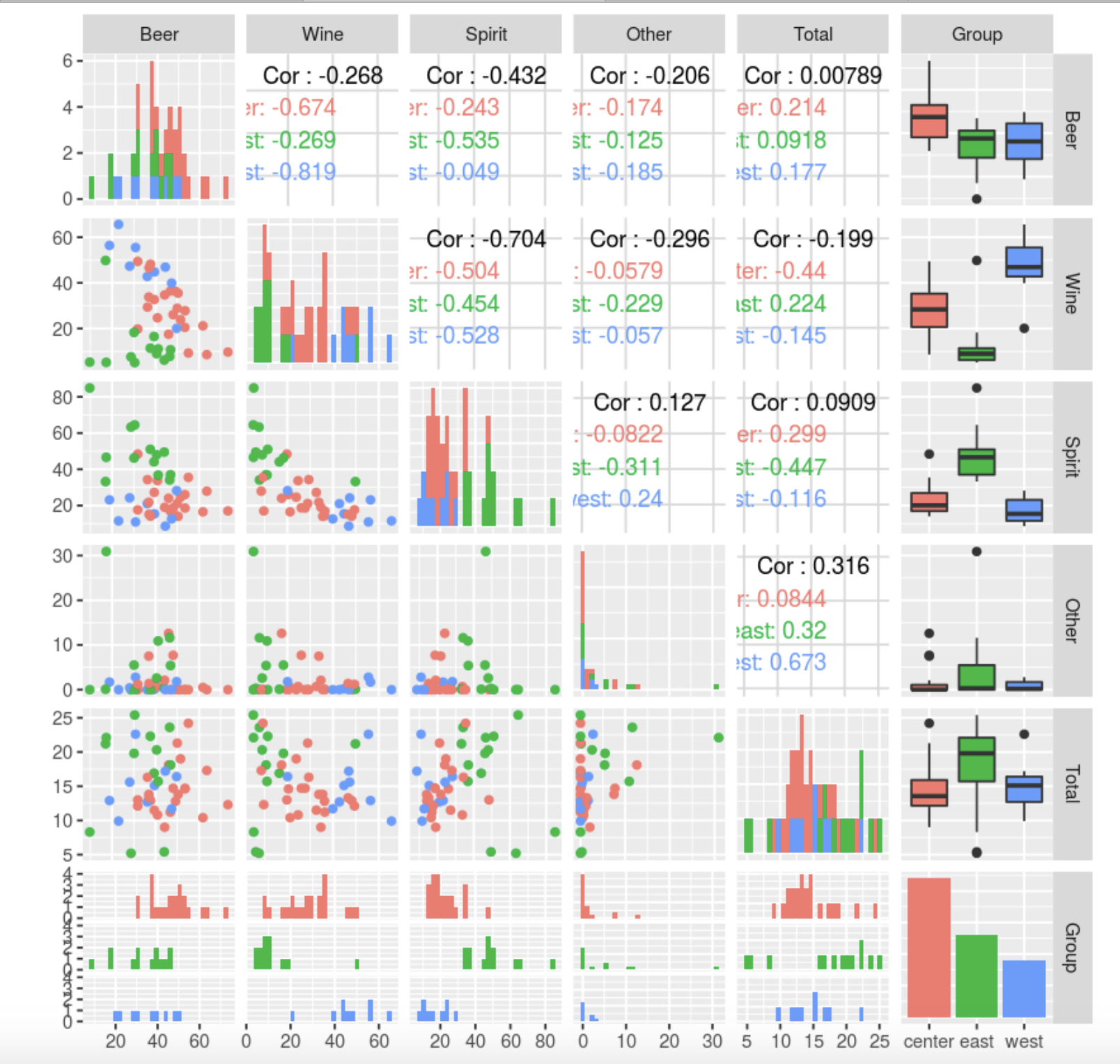
, , . Other, : , , , ( 10-12 , 45, , ). . , , , (). , , . Other .
, , — , — . , — , .
Total Other, . .
, Beer, Spirit Wine . , , , . , , , , , .
Total. , — .
data.group = data[,5]
data <- data[,-5]
data<- data[,-4]
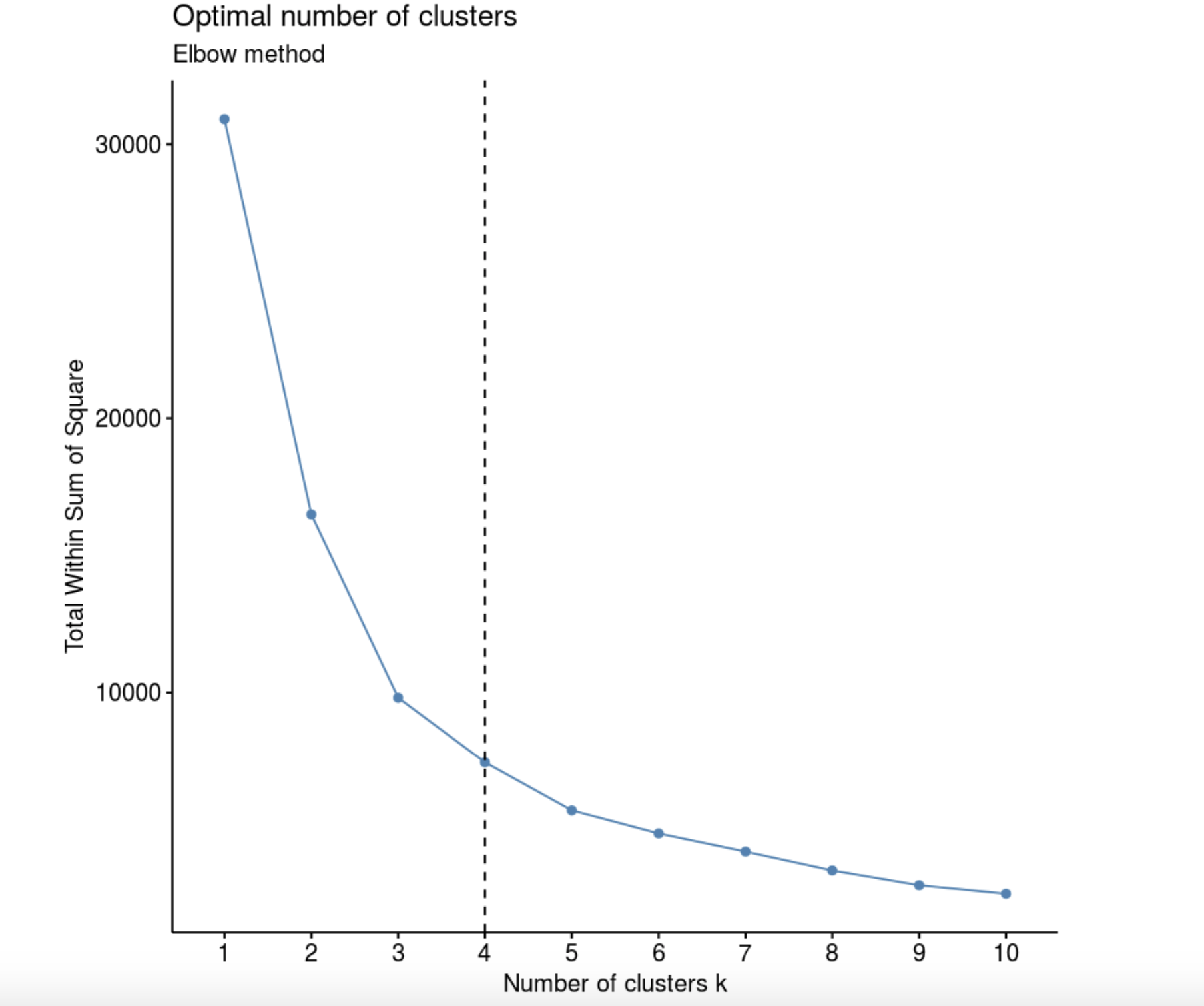
Elbow method (“ ”, “ ”). , k, – W(K), .
library(factoextra)
fviz_nbclust(data, kmeans, method = "wss") +
labs(subtitle = "Elbow method") +
geom_vline(xintercept = 4, linetype = 2)
data.dist <- dist((data))
hc <- hclust(data.dist, method = "ward.D2")
plot(hc, cex = 0.7)
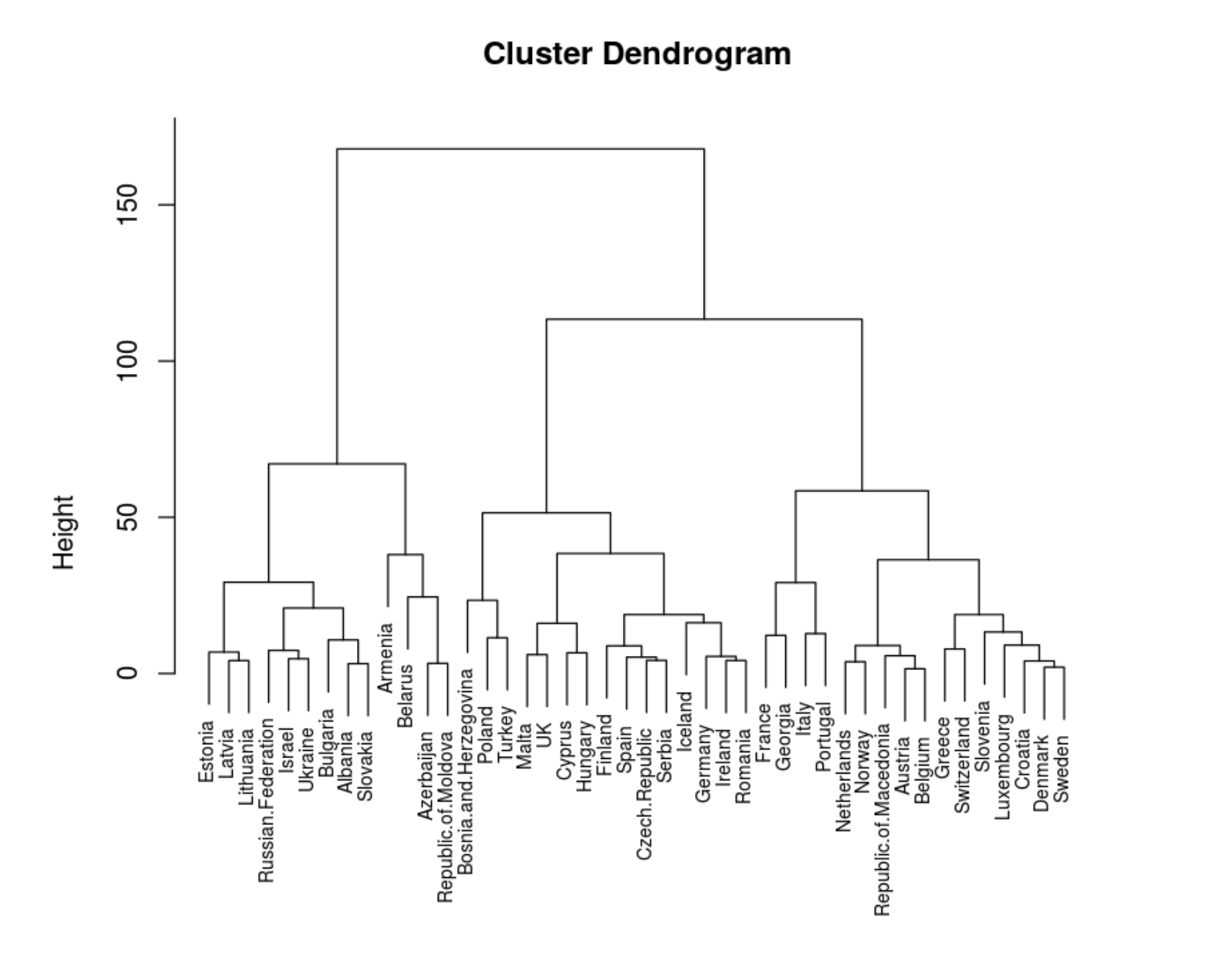
. .
colors=c('green', 'red', 'blue')
hcd = as.dendrogram(hc)
clusMember = cutree(hc, 4)
colLab <- function(n) {
if (is.leaf(n)) {
a <- attributes(n)
labCol <- colors[data.group[n]]
attr(n, "nodePar") <- c(a$nodePar, lab.col = labCol)
}
n
}
clusDendro = dendrapply(hcd, colLab)
plot(clusDendro, main = "Cool Dendrogram", type = "triangle")
rect.hclust(hc, k = 4)
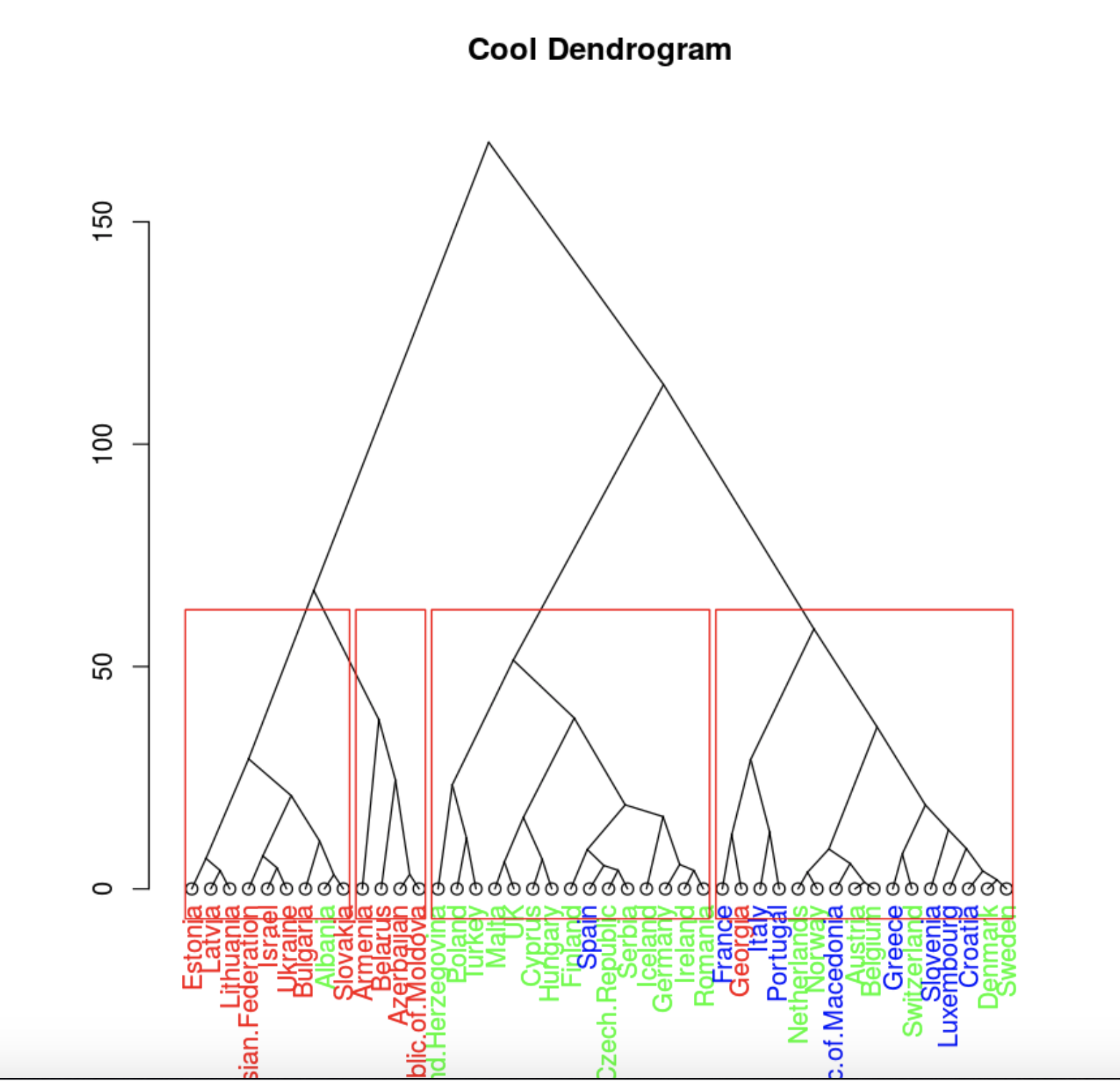
. , .
, , , 4 .
plot(clusDendro, main = "Cool Dendrogram", type = "triangle")
data.hclas_group <- factor(cutree(hc, k = 3))
rect.hclust(hc, k = 3)
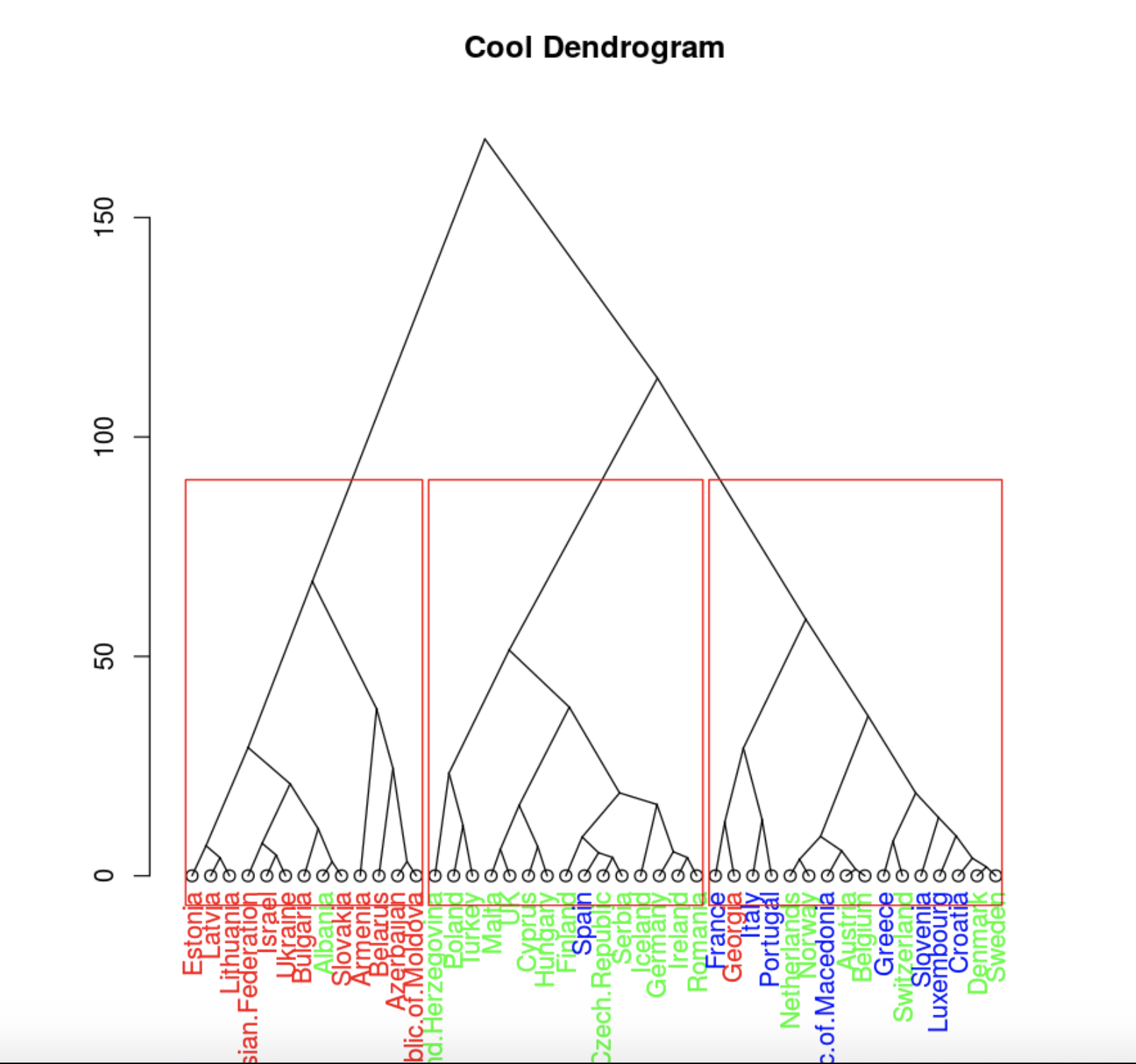
, , .
library(FactoMineR)
res.pca <- PCA(data,scale.unit=T, graph = F)
fviz_pca_biplot(res.pca,
col = colors[data.hclas_group], palette = "jco",
label = "var",
ellipse.level = 0.8,
addEllipses = T,
col.var = "black",
legend.title = "groups4")
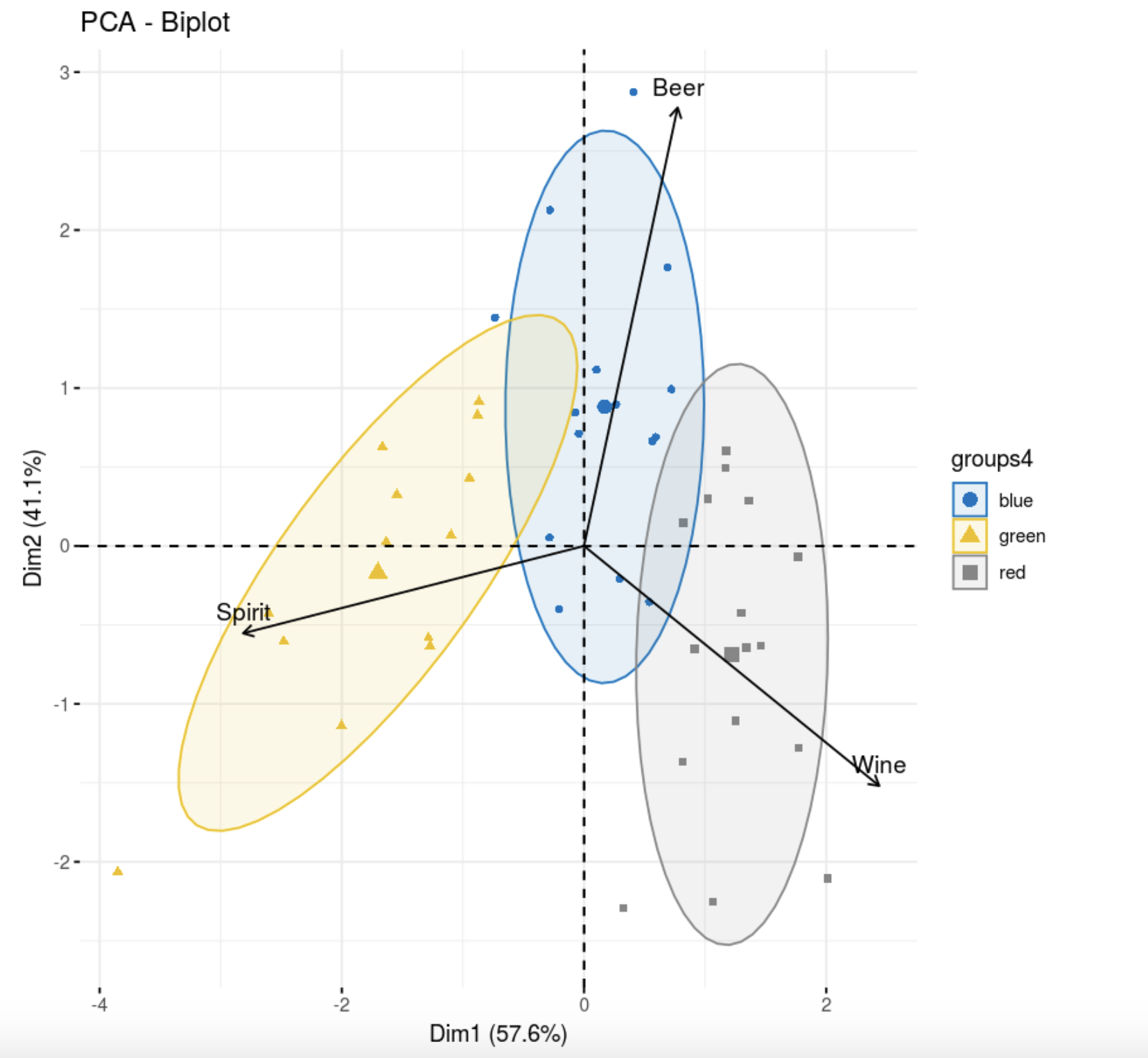
, , . , , , , . , , , k-++.
library(flexclust)
data.kk <- kcca(data, k=3, family=kccaFamily("kmeans"),
control=list(initcent="kmeanspp"))
fviz_pca_biplot(res.pca,
col.ind =as.factor(data.kk@cluster), palette = "jco",
label = "var",
ellipse.level = 0.8,
addEllipses = T,
col.var = "black", repel = TRUE,
legend.title = "clusters")
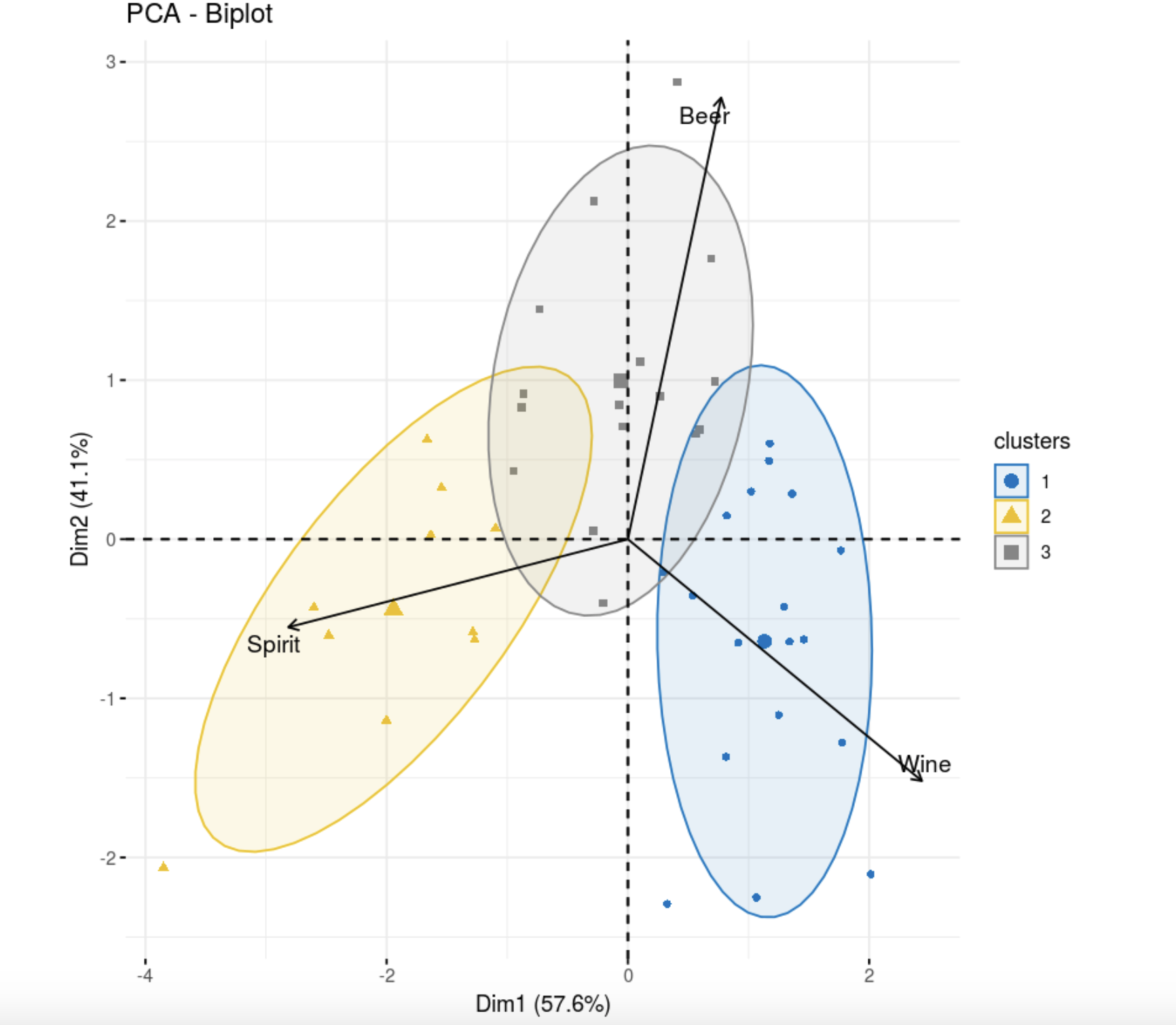
, k- . , , .
, , hclust. .

, , . . , .
. . , , , . , , . , .
Il serait possible d'effectuer un regroupement basé sur l'hypothèse de modèles de regroupement en utilisant des critères d'information ( voici la description ), et d'essayer également l'analyse discriminante classique pour cet ensemble de données. Si cet article vous a été utile, j'ai l'intention de publier une suite.