La guilloché est un motif caractéristique du papier-monnaie et d'autres titres. Une histoire détaillée à leur sujet avec une digression dans l'histoire peut être trouvée dans l'article précédent . Un algorithme de dessin qui construit des guilloches par points y a également été donné.Tout à fait inutile, il convient de noter si nous les dessinons non seulement pour le plaisir, mais à des fins pratiques - par exemple, pour ajouter ces mêmes valeurs au design. Des milliers de points ne feront que ralentir l'éditeur, mais il ne pourra pas afficher le résultat de toute façon - au lieu de vraies lignes continues, il y aura une sorte de résultat de la moyenne des points, faite comme Dieu mettrait une âme dessus.Par conséquent, le moment est venu de penser à un autre algorithme - qui donnerait immédiatement des vecteurs. Étant donné que les éditeurs communs pour les lignes courbes n'offrent qu'une interpolation par les courbes de Bézier, nous nous concentrerons sur eux.En fait, l'algorithme est simple - et beaucoup plus simple que celui décrit dans la première partie. Nous prenons deux courbes d'enveloppe, définissons le nombre d'ondes qui devraient tenir sur 360 degrés, nous estimons à quel angle et avec quelle courbure le vrai guilloché doit passer du point actuel au suivant, et l'interpolons avec quatre courbes de Bézier.Voici un programme en Asymptote, qui est extrêmement pratique pour de telles choses.import graph;
size(1000,1000);
xaxis(ticks=Ticks);
yaxis(ticks=Ticks);
defaultpen(2);
var zero = (0,0);
real tens(bool at_top, real angle)
{
return angle/180;
}
guide wave(path top, path bottom, int parts, real offset)
{
guide w;
real step = 1/parts;
real half = step/2;
pair[] top_pt;
pair[] bot_pt;
pair[] top_dir;
pair[] bot_dir;
real[] top_angle;
real[] bot_angle;
for(int i: sequence(0,parts-1))
{
real rel = i*step + step*offset;
real top_time = reltime(top, rel);
real bot_time = reltime(bottom, rel+half);
top_pt[i] = point(top, top_time);
bot_pt[i] = point(bottom, bot_time);
top_dir[i] = dir(top, top_time);
bot_dir[i] = dir(bottom, bot_time);
}
for(int i: sequence(0,parts-1))
{
int prev = i == 0 ? parts-1 : i-1;
int next = i == parts-1 ? 0 : i+1;
var v1 = bot_pt[i] - top_pt[i];
var v2 = bot_pt[prev] - top_pt[i];
var a = degrees(v2) - degrees(v1);
top_angle[i] = a<0 ? 360+a : a;
v1 = top_pt[i] - bot_pt[i];
v2 = top_pt[next] - bot_pt[i];
a = degrees(v2) - degrees(v1);
bot_angle[i] = a<0 ? 360+a : a;
}
for(int i: sequence(0,parts-1))
{
int next = i == parts-1 ? 0 : i+1;
var l1 = length(top_pt[i]--bot_pt[i]);
pair ctl1 = top_pt[i] + top_dir[i] * tens(true, top_angle[i]) * l1;
pair ctl2 = bot_pt[i] - bot_dir[i] * tens(false, bot_angle[i]) * l1;
w = w .. top_pt[i] .. controls ctl1 and ctl2 .. bot_pt[i];
var l2 = length(bot_pt[i]--top_pt[next]);
ctl1 = bot_pt[i] + bot_dir[i] * tens(false, bot_angle[i]) * l2;
ctl2 = top_pt[next] - top_dir[next] * tens(true, top_angle[next]) * l2;
w = w .. bot_pt[i] .. controls ctl1 and ctl2 .. top_pt[next];
}
return w;
}
void repeat(int count, path top, path bottom, int parts)
{
real step = 1/count;
for(int i: sequence(0, count-1))
{
draw(wave(top, bottom, parts, step*i));
}
}
path normalize(path p)
{
var min = min(p);
var max = max(p);
var top_center = min + ((max.x-min.x)/2, (max.y-min.y)/2);
return scale(20*1/(max-min).x)*shift(zero - top_center)*p;
}
path top = (338.499521684,-159.274266483)
..controls (327.252951684,-158.148796483) and (323.448961684,-145.618286483) .. (318.743661684,-137.260595483)
..controls (309.897671684,-123.808725483) and (292.025851684,-123.657732483) .. (278.251471684,-118.807470483)
..controls (272.669581684,-117.510629483) and (268.731931684,-109.221757483) .. (274.571781684,-105.645360483)
..controls (281.545351684,-101.031122483) and (290.488261684,-97.7906864833) .. (293.317871684,-89.0437964838)
..controls (296.611021684,-81.8498064838) and (293.894071684,-73.5853264838) .. (295.556161684,-66.3445764838)
..controls (299.563831684,-59.7686064838) and (308.181311684,-64.5344964838) .. (312.903811684,-67.4344264838)
..controls (325.368171684,-74.9872364838) and (341.157891684,-80.6126364838) .. (355.257331684,-73.9383264838)
..controls (363.506651684,-70.9246164838) and (370.115991684,-63.9703964838) .. (378.731941684,-62.0926264838)
..controls (384.688491684,-61.4010364838) and (389.980631684,-67.6129964838) .. (387.306161684,-73.3211464838)
..controls (385.256921684,-82.8346964838) and (388.441441684,-93.9447564833) .. (397.757331684,-98.3016064833)
..controls (403.144721684,-101.085582483) and (412.671611684,-104.606352483) .. (410.331551684,-112.414892483)
..controls (406.654931684,-119.718595483) and (396.921641684,-119.937732483) .. (390.144051684,-122.524267483)
..controls (378.065751684,-125.483516483) and (364.313841684,-130.717262483) .. (359.884541684,-143.562216483)
..controls (356.731021684,-151.157386483) and (350.818391684,-160.192046483) .. (341.435061684,-159.293796483)
..controls (340.456461684,-159.306096483) and (339.478031684,-159.281196483) .. (338.499521684,-159.274296483)
--cycle;
top = normalize(top);
bottom = scale(0.5)*top;
top = ellipse(zero, 4, 6);
bottom = ellipse(zero, 2, 3);
top = circle(zero, 5);
bottom = circle(zero, 3);
repeat(12, top, bottom, 8);
Le cas le plus compréhensible est celui où les sinusoïdes sont situées entre deux cercles.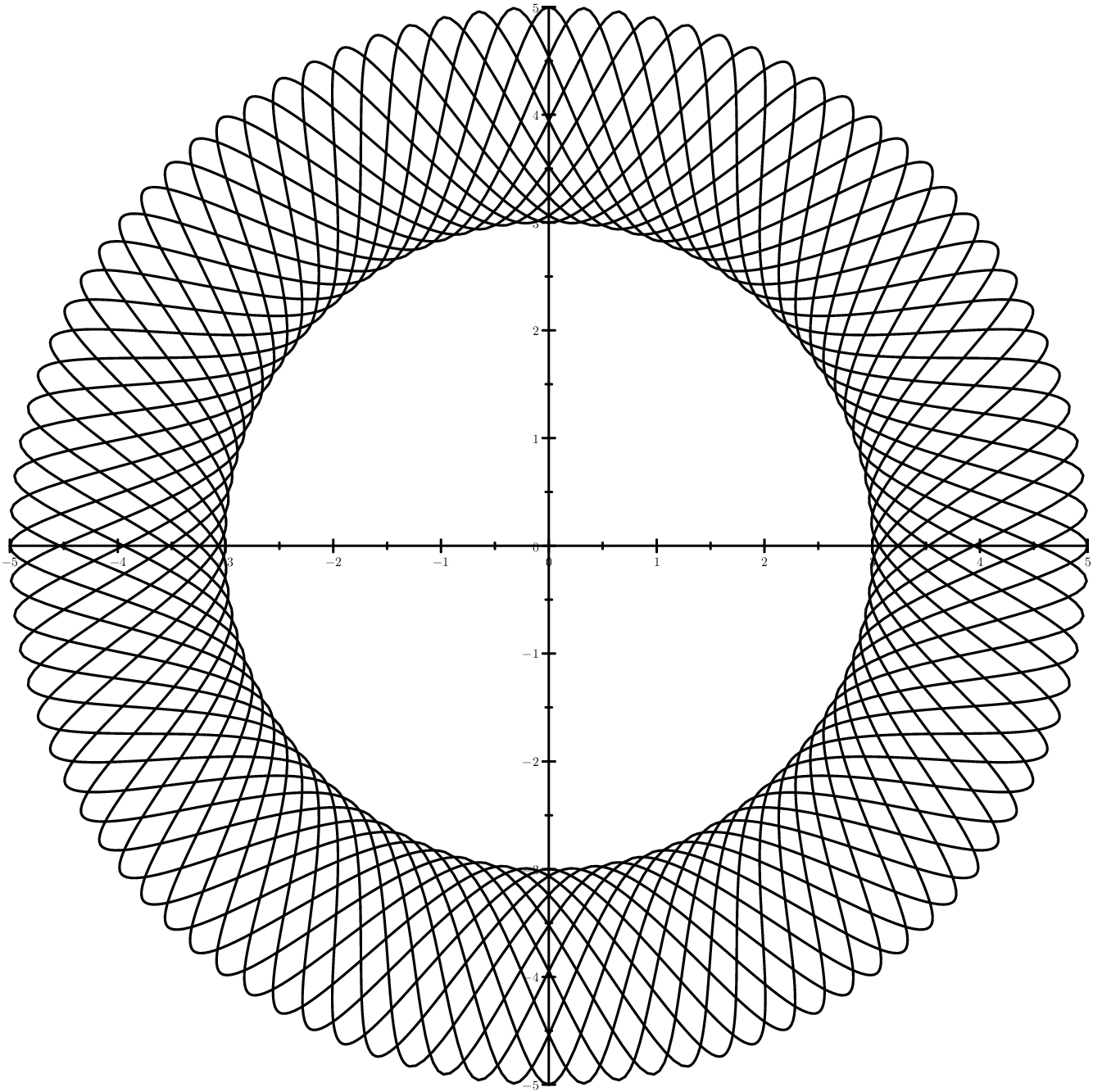
Le cas est plus rusé - des ellipses au lieu de cercles.
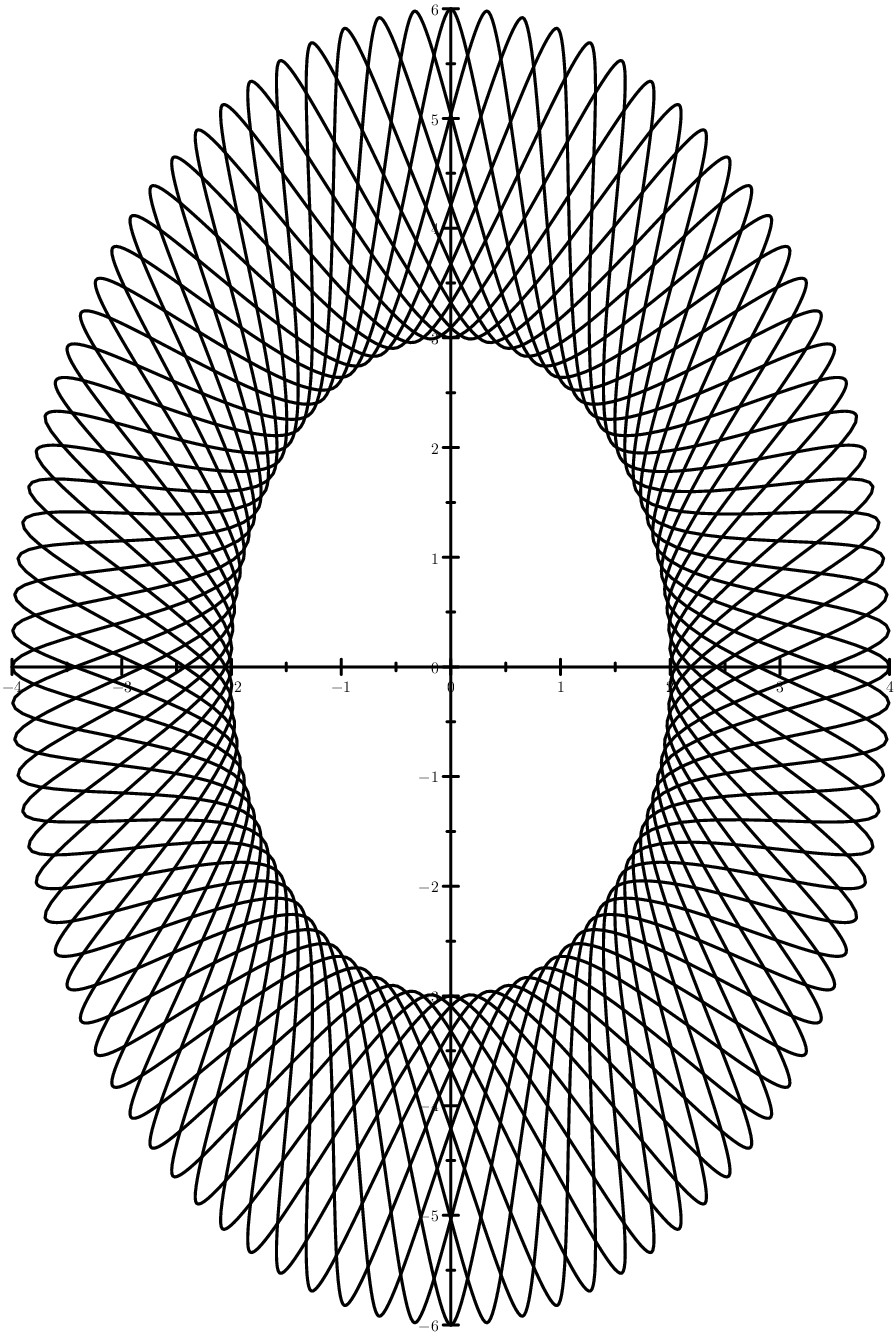Et une image proche de l'usage industriel: la guilloché, formant une sorte de débouché artistique.
Ici, le résultat n'est cependant pas parfait. Tout d'abord, la fonction des dizaines a dû être ajustée pour qu'elle renvoie toujours une «tension» constante de 0,5. Et deuxièmement, les courbes ne sont pas très symétriques, et dans la partie gauche près de l'axe X, elles sont en quelque sorte confuses. Bien sûr, tout cela peut être corrigé à la main, surtout si vous faites des billets pour l'État et que vous avez des artistes très qualifiés, mais vous pouvez essayer d'augmenter la précision des calculs, car ils s'égarent évidemment à certains points où la courbure de l'enveloppe change brusquement.La guilloché étant interpolée, la question se pose: coïncident-elles pour ainsi dire «réelles», c'est-à-dire dessinées par des points. Étant nouveau dans la géométrie différentielle, j'ai du mal à le dire, mais plutôt «non» que «oui».Mais qui voit vraiment la différence?Et l'avantage pratique est indéniable - avec quelques dizaines de courbes de Bézier, il est beaucoup plus facile de travailler qu'avec mille points, et elles offrent beaucoup plus de possibilités de conception.De plus, cet algorithme peut également être amélioré. Deux options se suggèrent immédiatement:a) spécifiez un nombre différent de points sur la courbe externe et interne, puis l'effet de broyer le motif plus près du centre ne sera pas créé, comme dans les exemples avec un cercle et une ellipse.b) placer les points sur les enveloppes de manière non uniforme, mais, par exemple, en les faisant plus souvent, moins souvent, ce qui ajoutera une nouvelle dimension au motif.