Algorithme génétique Python pour trouver des extrema globaux

Contexte

Récemment, dans le cadre d'activités de formation, j'ai eu besoin d'utiliser le bon ancien algorithme génétique afin de trouver les fonctions minimum et maximum de deux variables. Cependant, à ma grande surprise, il n'y avait pas d'implémentation similaire sur python sur Internet, et cette section n'était pas couverte dans l'article Wikipedia sur l'algorithme génétique.



J'ai donc décidé d'écrire mon petit package en Python avec une visualisation de l'algorithme, selon lequel il sera commode de configurer cet algorithme et de rechercher les subtilités du modèle sélectionné.

Dans ce court article, je voudrais partager le processus, les observations et les résultats.

Le principe de l'algorithme

Je ne parlerai pas du principe global du travail des algorithmes génétiques, mais si vous n'en avez pas entendu parler, alors vous pourrez vous familiariser avec lui sur Wikipédia .

Pour le moment, le package implémente une seule GA, qui est paramétrée par les données d'entrée via un guiche simple. Je vais vous parler brièvement des fonctions génétiques sélectionnées et des solutions algorithmiques de base.

L'individu monochromosomal porte dans chacun de ses gènes des informations sur la coordonnée x ou y correspondante. Une population est déterminée par de nombreux individus, mais la population est segmentée en 4 individus. Cette solution, bien sûr, est due à une tentative d'éviter la convergence vers un optimum local, car la tâche est de trouver un extremum global. Une telle partition, comme l'a montré la pratique, dans de nombreux cas ne permet pas à un génotype de dominer dans l'ensemble de la population, mais au contraire donne à «l'évolution» une plus grande dynamique. Pour chacune de ces parties de la population, l'algorithme suivant est appliqué:

1. La sélection s'effectue de manière similaire à la méthode de classement. 3 individus sont sélectionnés avec les meilleurs indicateurs de fonction de fitness (c'est-à-dire que les individus sont triés dans l'ordre croissant / décroissant de la fonction définie par l'utilisateur, qui agit comme la fonction d'adaptation).
2. Ensuite, la fonction de croisement est appliquée de manière à ce qu'une nouvelle génération (ou plutôt un nouveau segment d'une population de 4 individus) reçoive 2 paires de gènes non muets d'un individu avec une meilleure indication de la fonction fitness et une paire de gènes mutés de deux autres individus. Plus d'informations sur la compilation de la fonction de mutation seront écrites dans la section suivante.

Le principe de fonctionnement de la sélection, du croisement et de la mutation ressemble clairement à ceci (dans la génération N, les chromosomes des individus sont déjà triés dans le bon ordre, et un petit carré noir signifie mutation):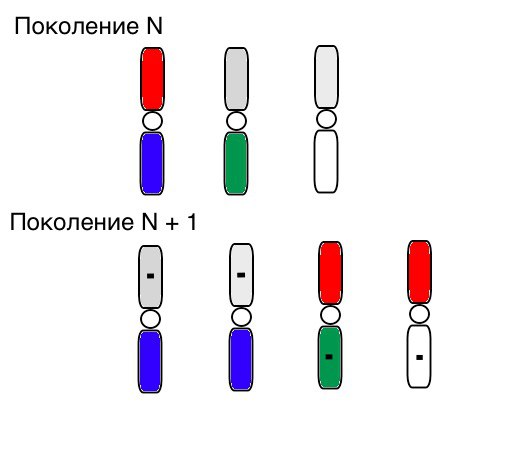

Tests et observations primaires

Nous testons donc cet algorithme sur deux exemples simples:

Test 1

$$

$$f(x, y) = sin(x) + cos(y)$$

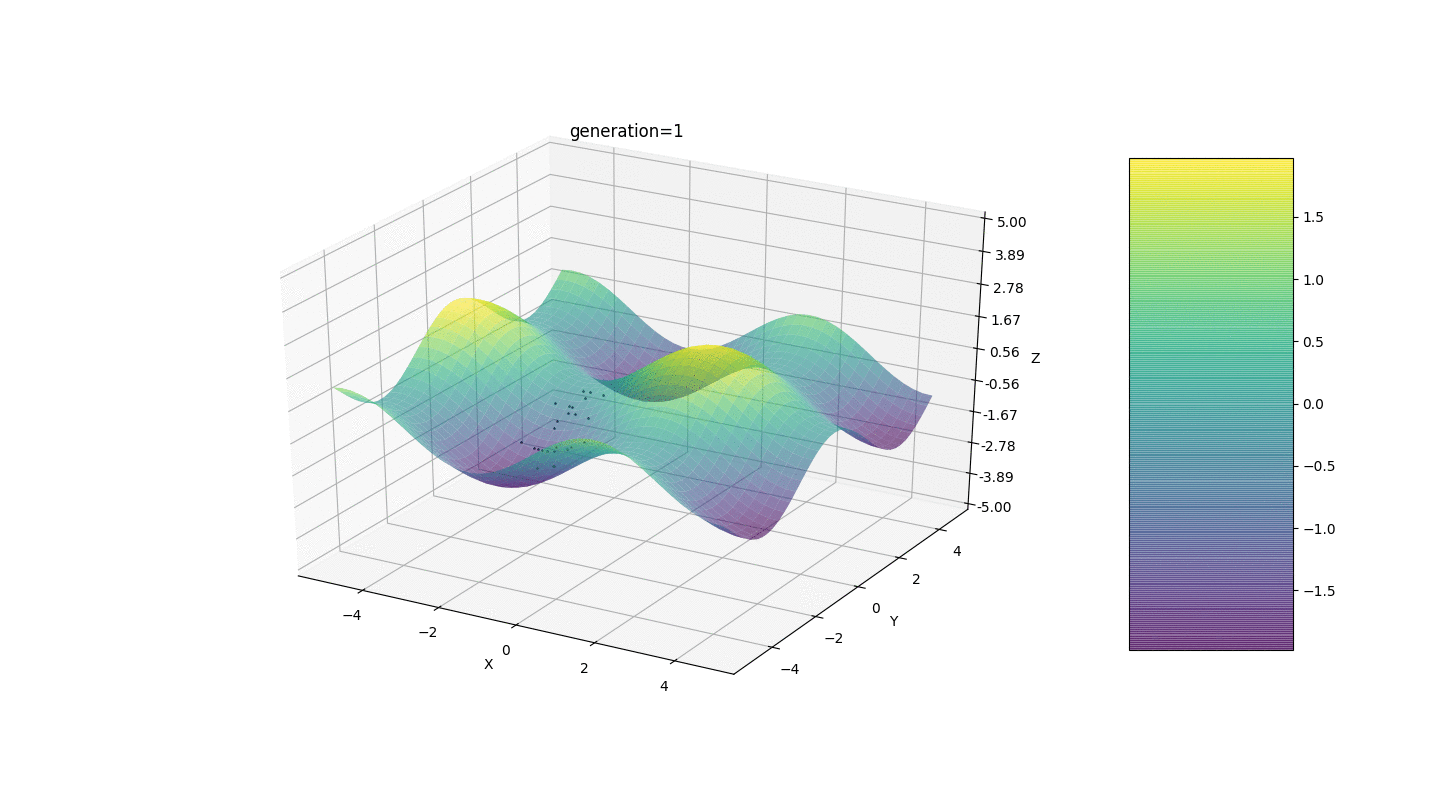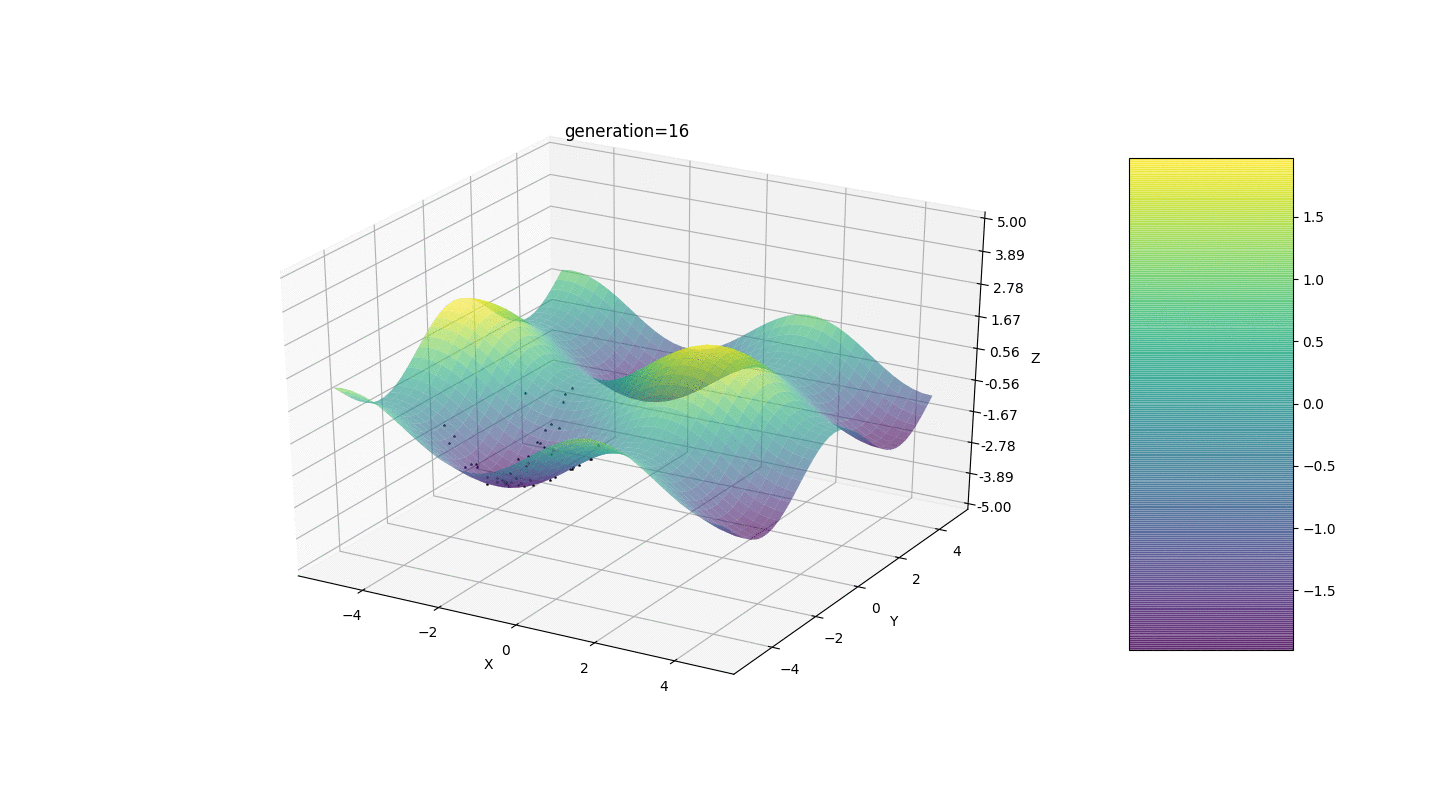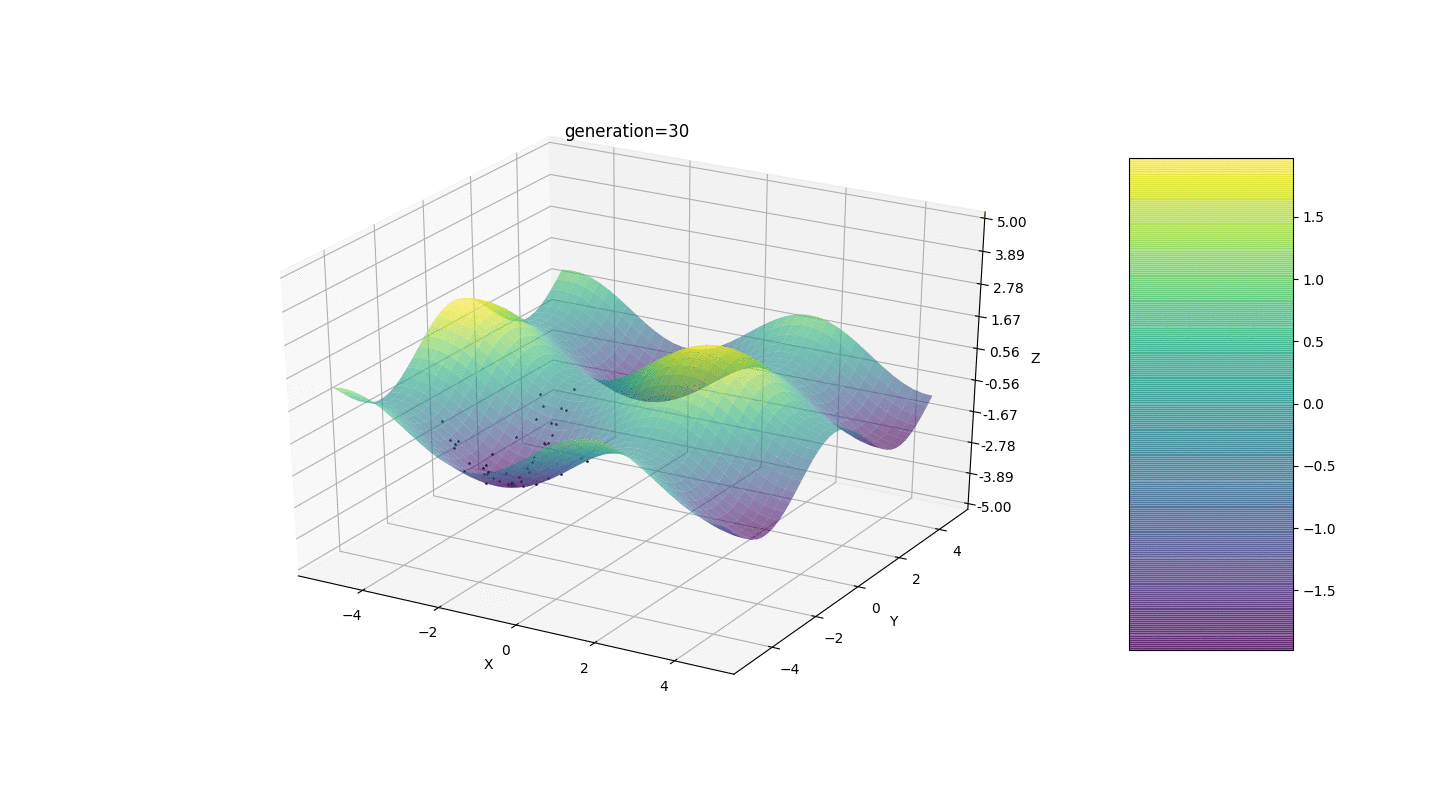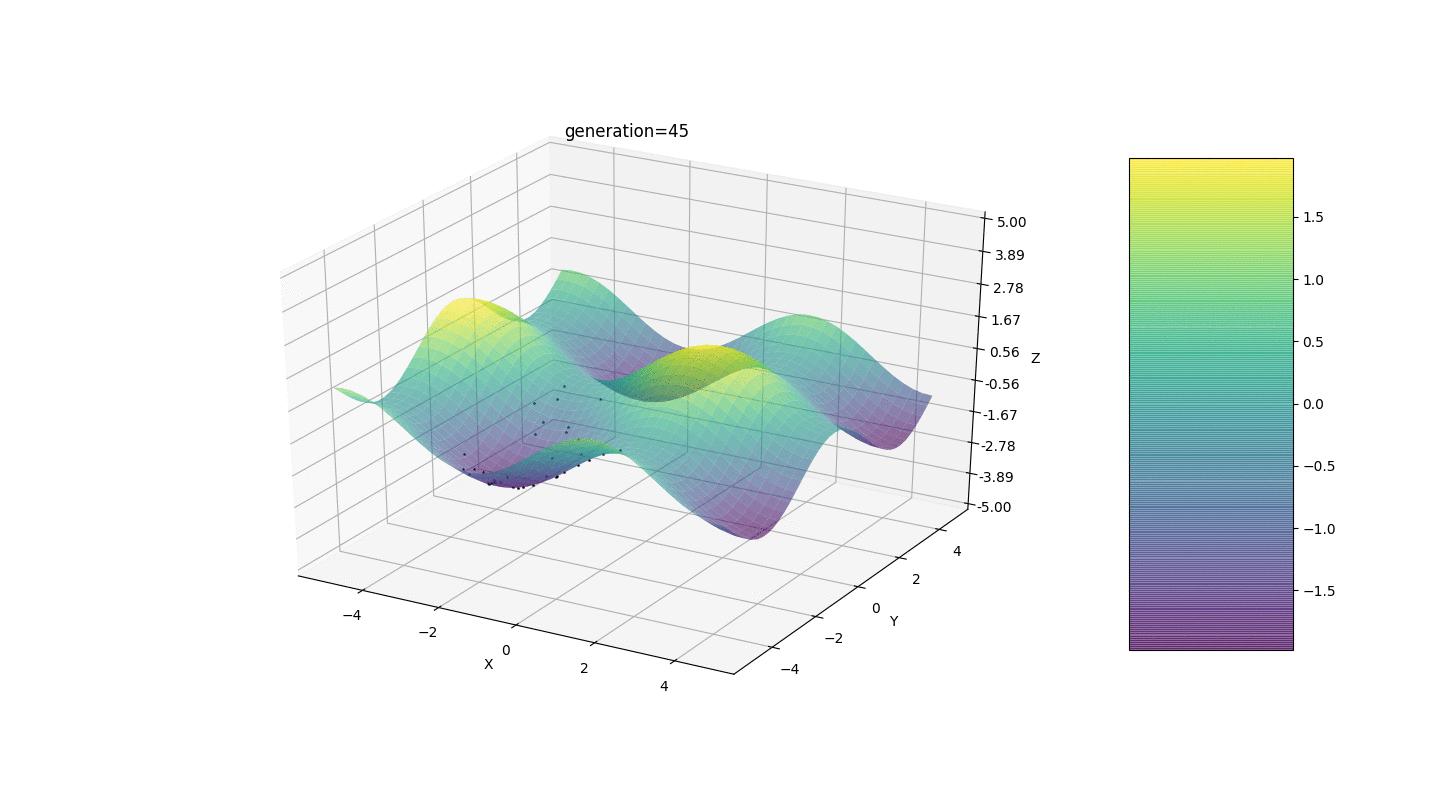
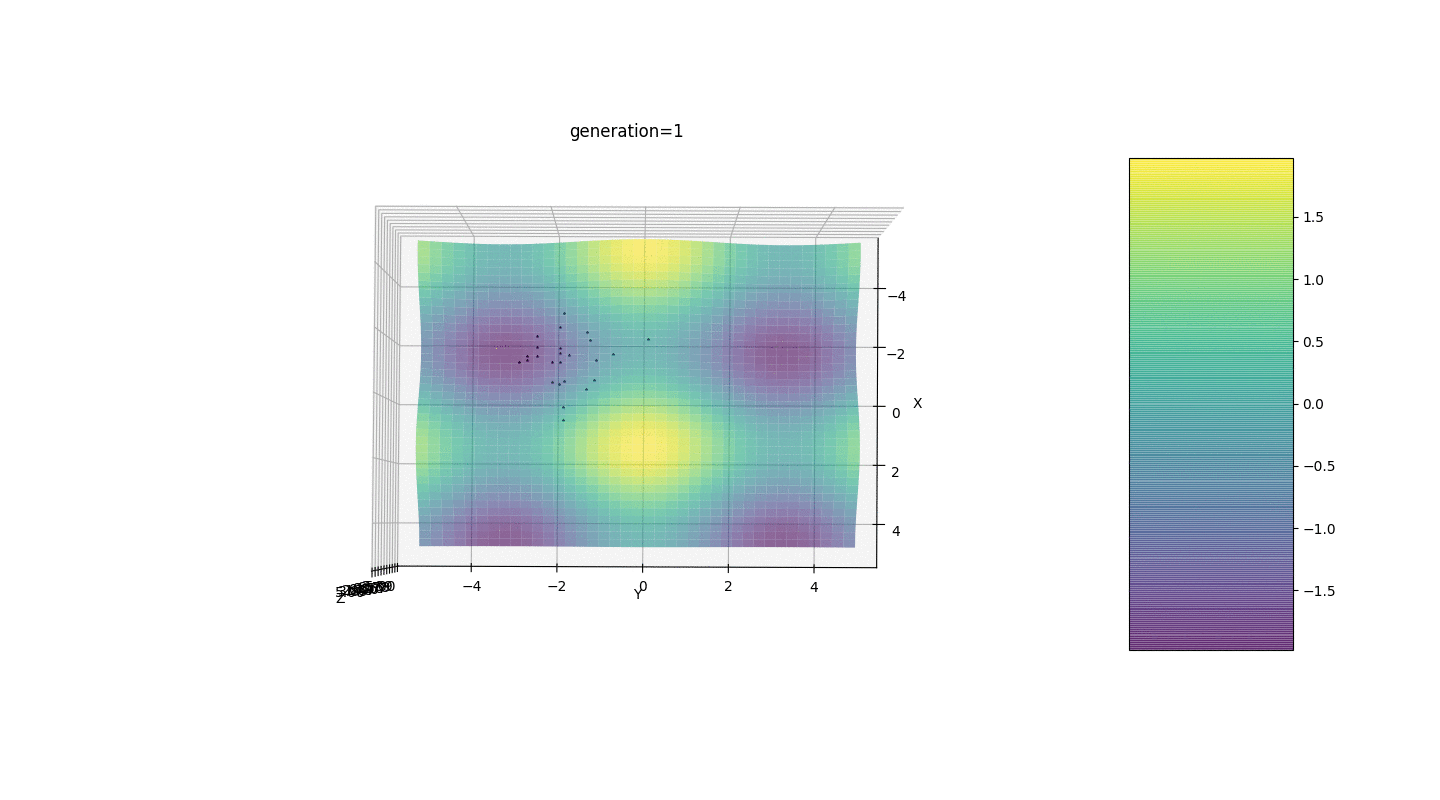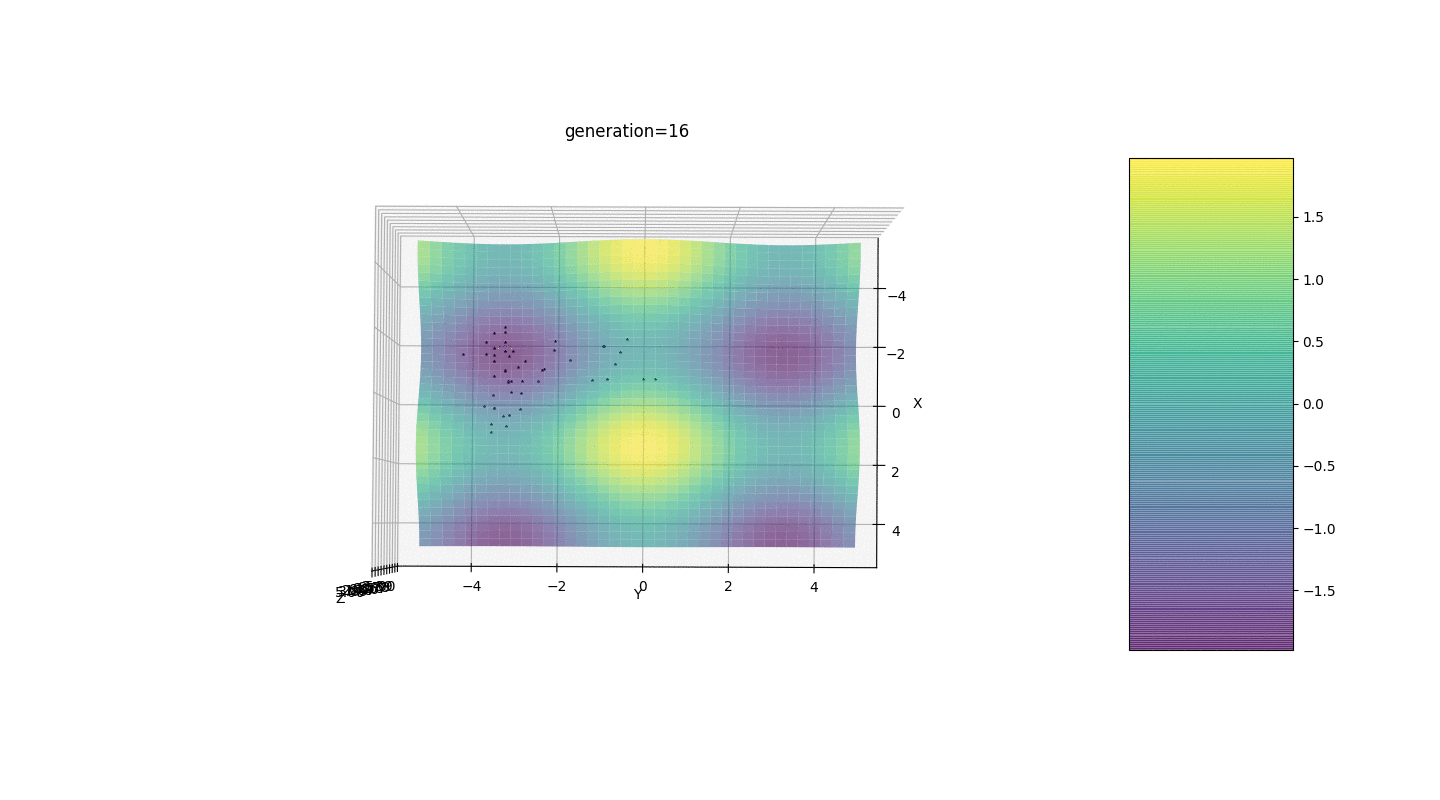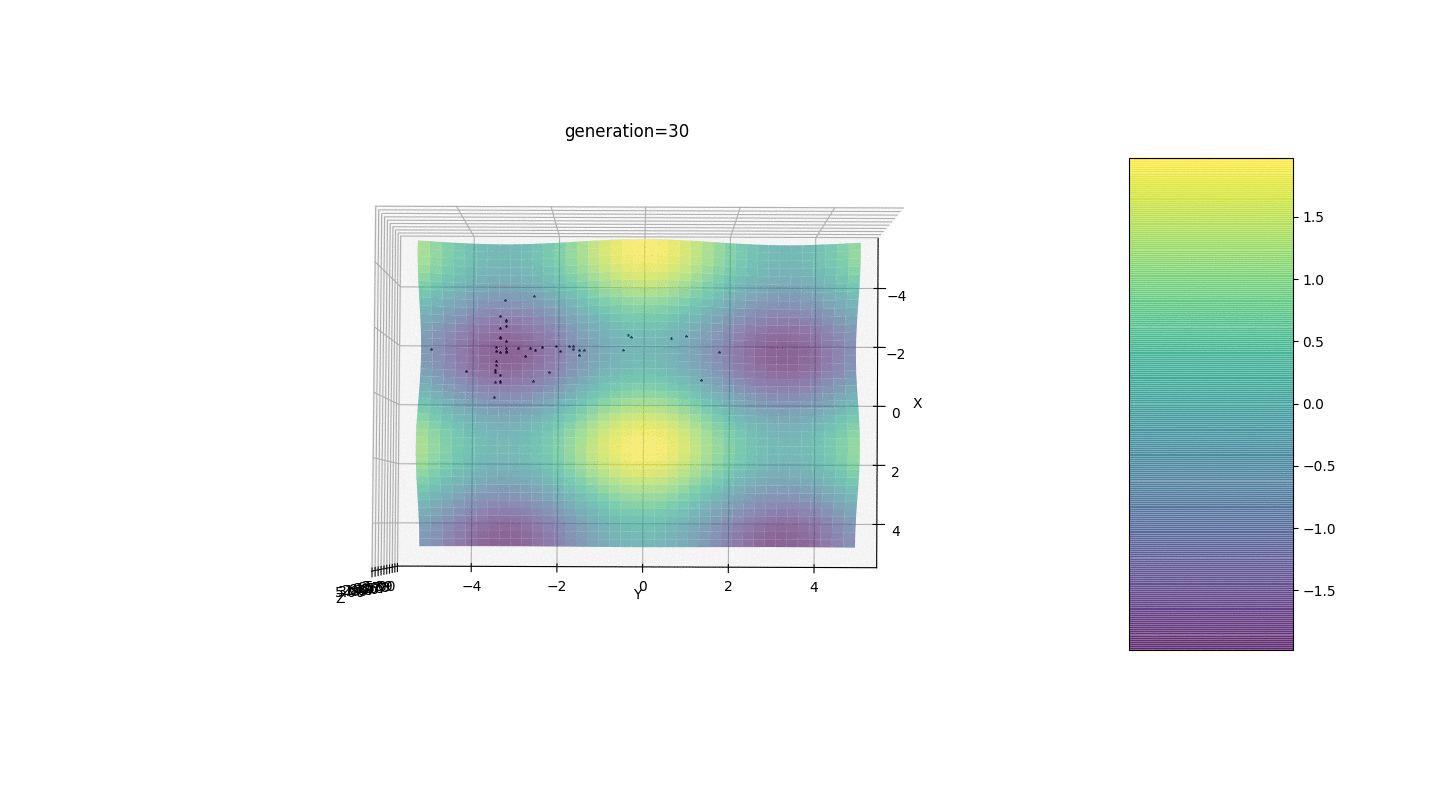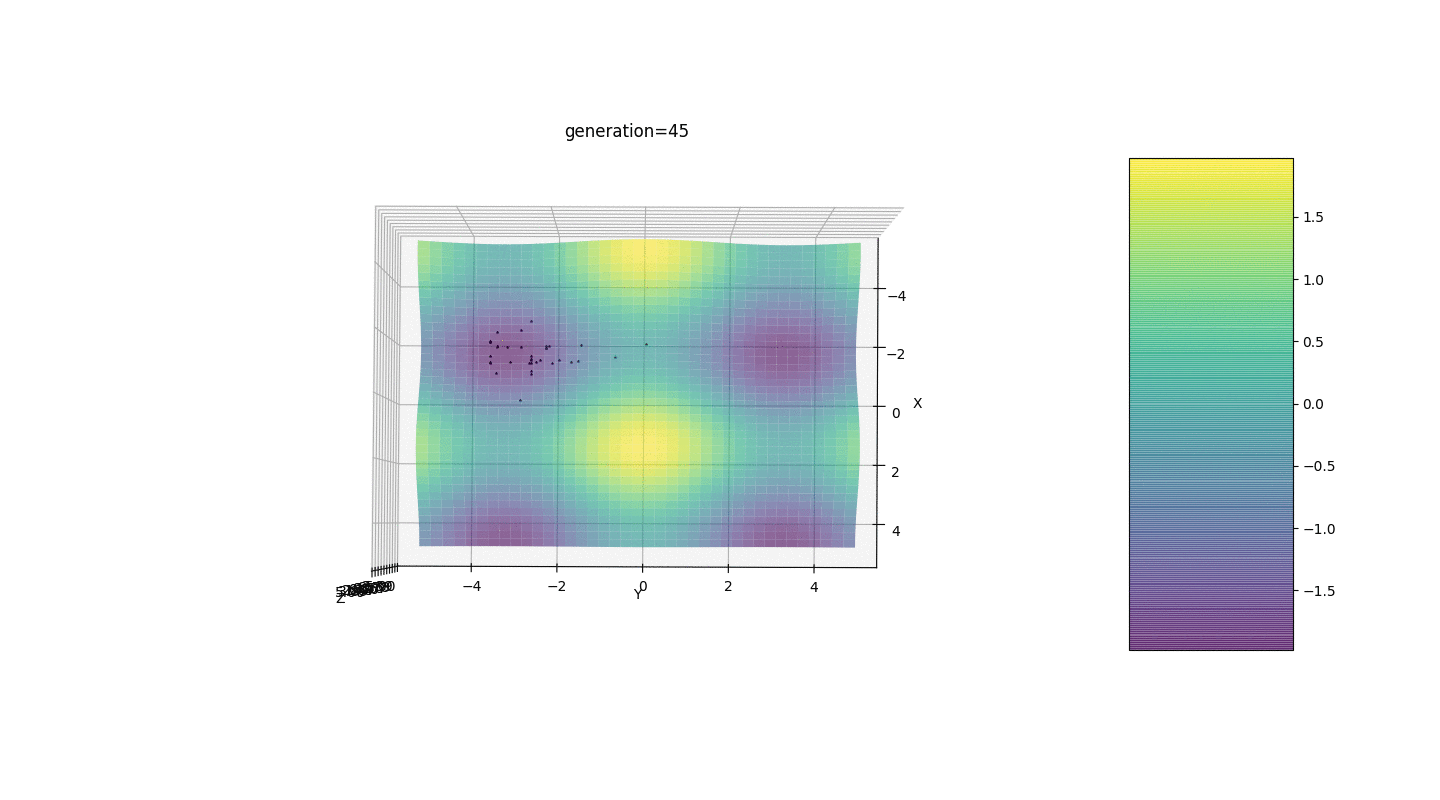
Test 2

$$

$$\frac{4 \sqrt{x} - 5y }{ 3x ^ 2 + 2 y ^ 2 - 2 x + 1}$$

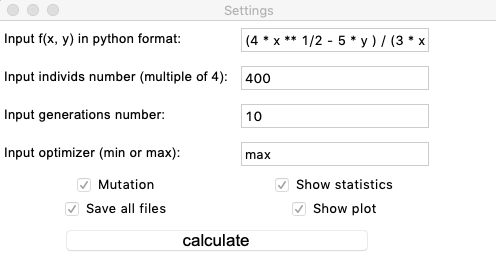
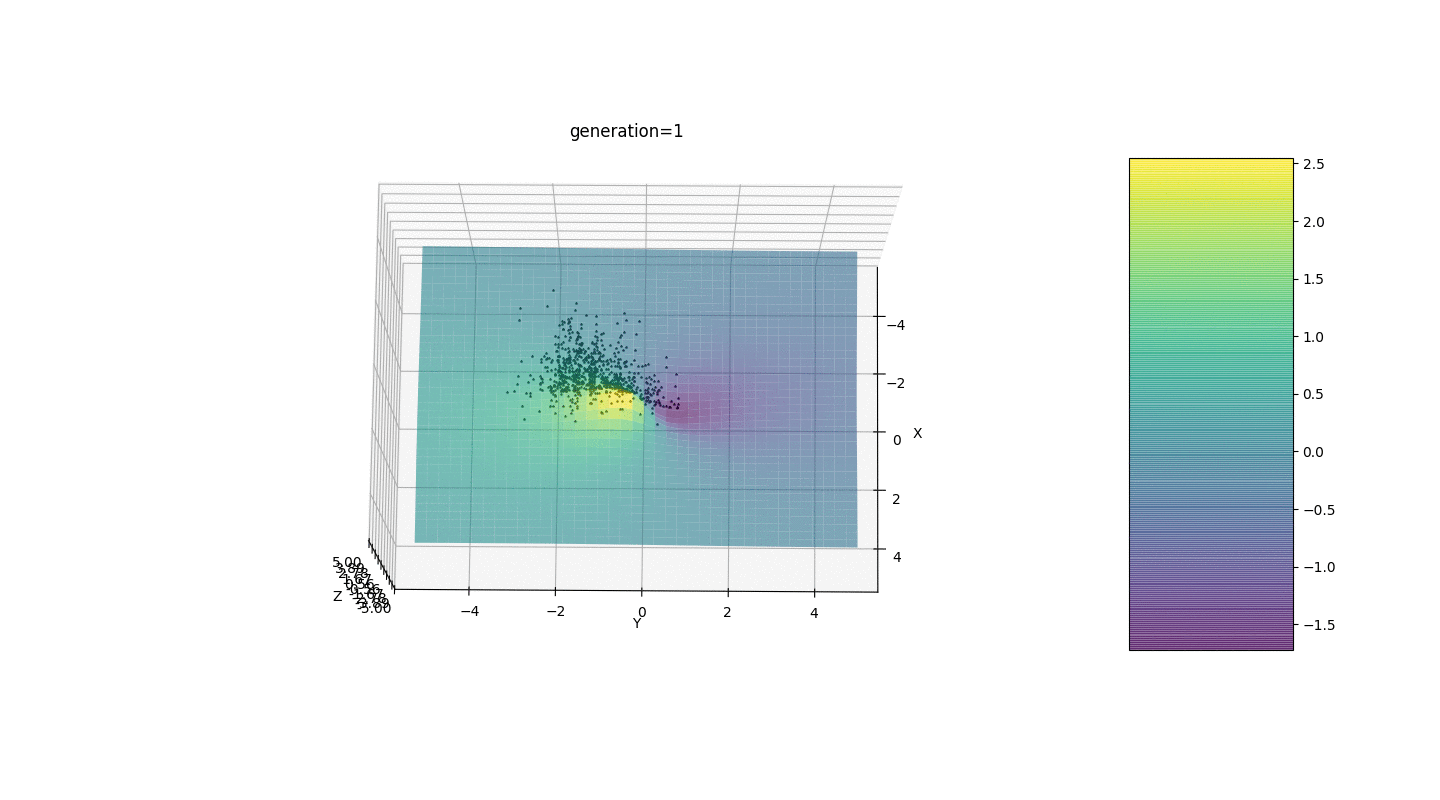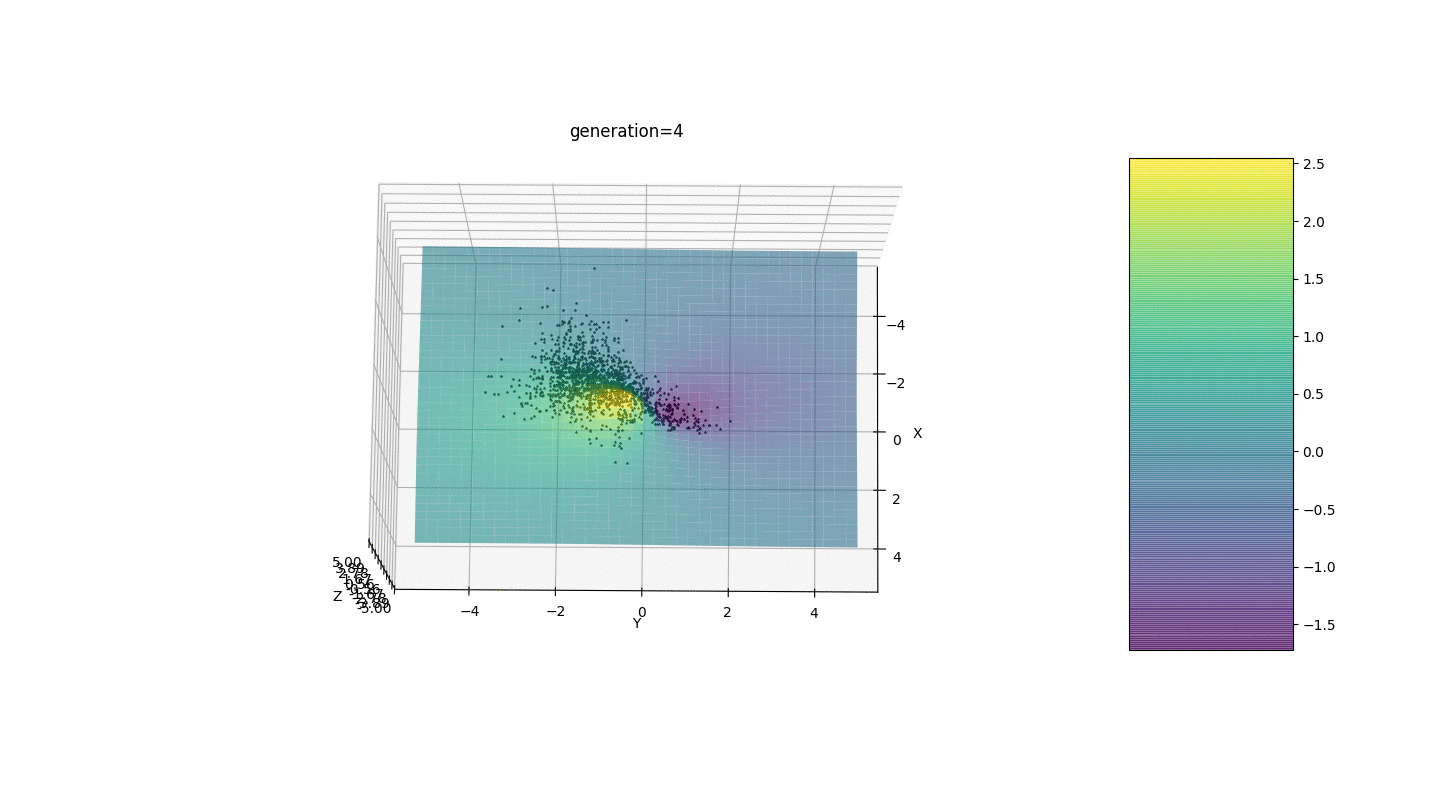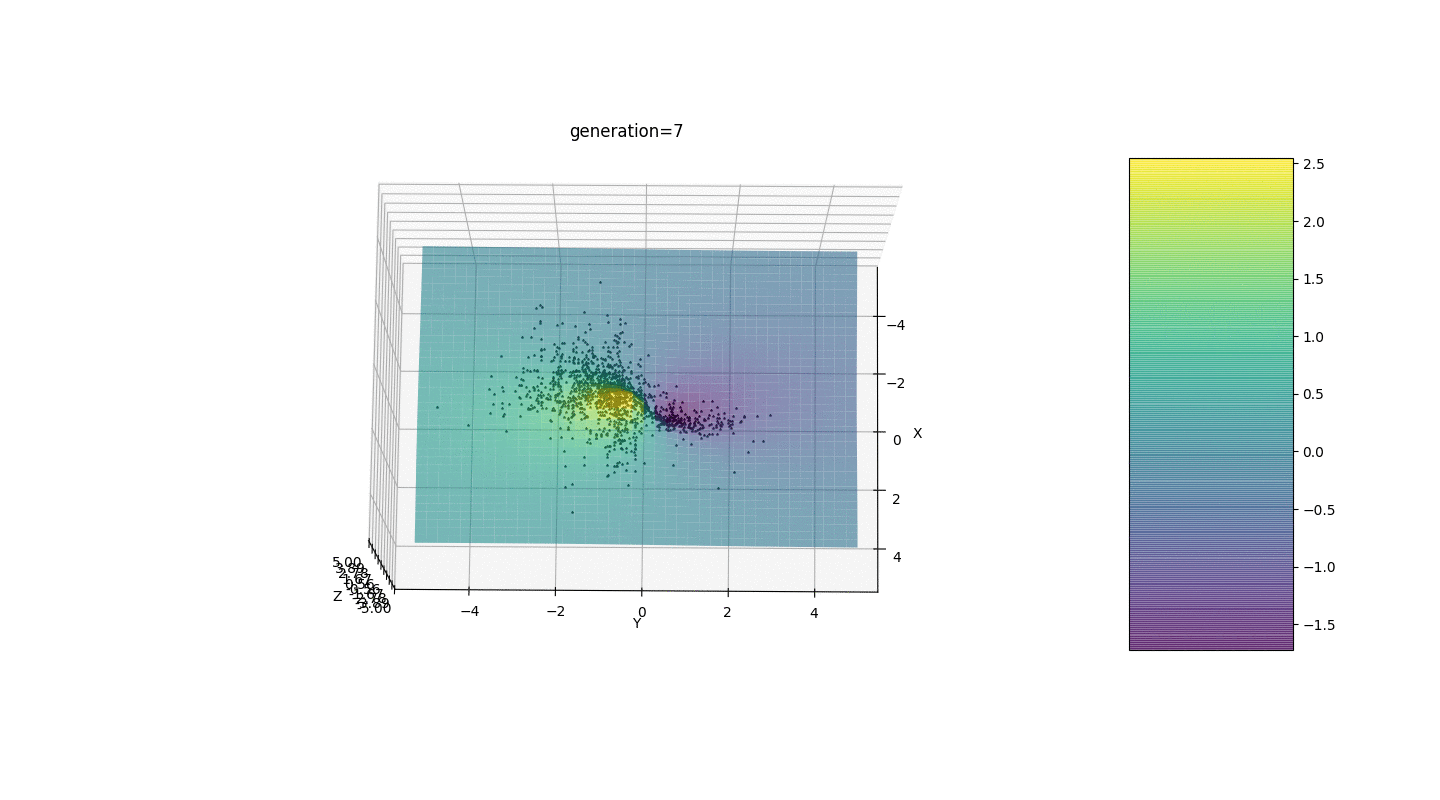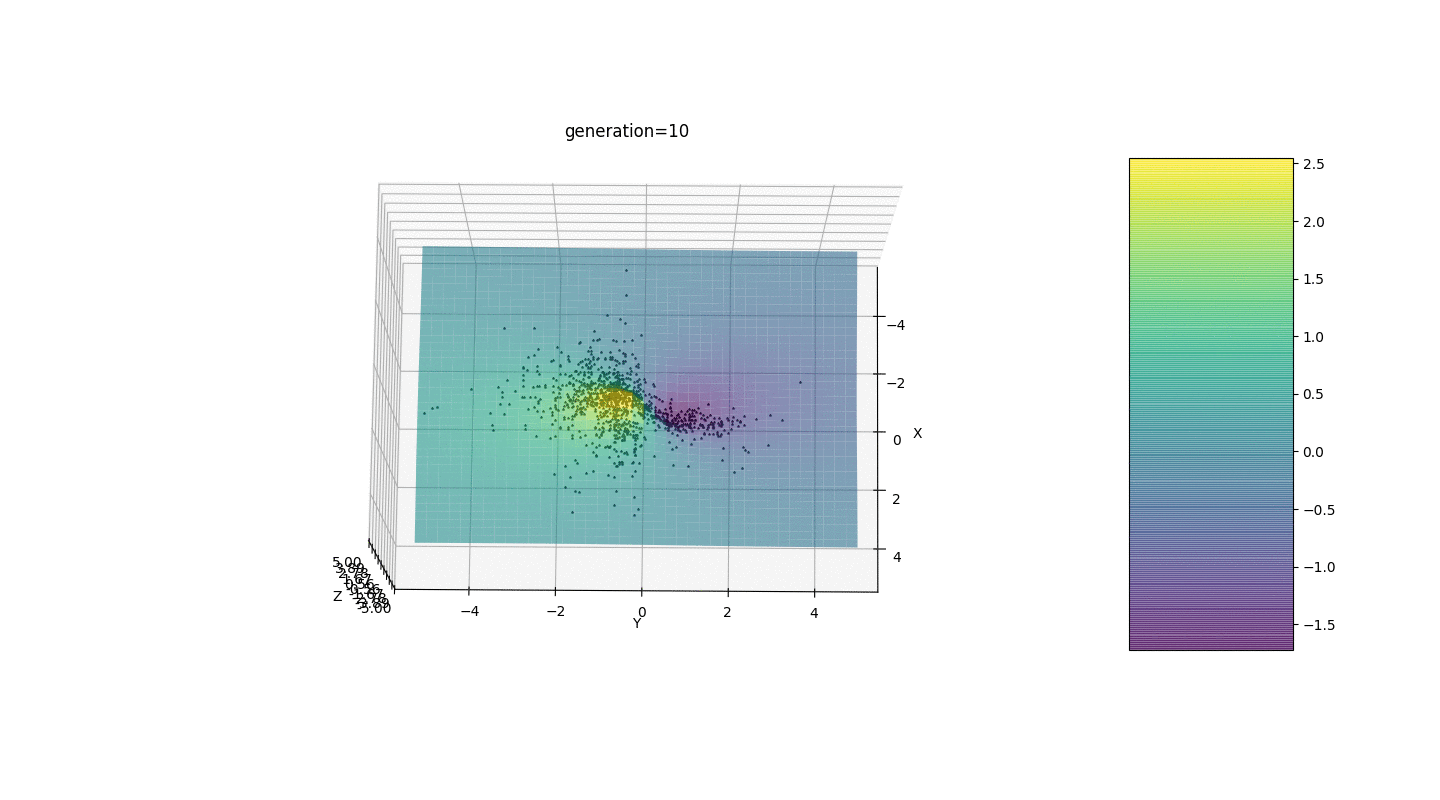
Après avoir testé et étudié le fonctionnement de l'algorithme par la méthode du regard et du poke aléatoire, plusieurs hypothèses-schémas ont été révélées:

• L'erreur de l'algorithme est directement proportionnelle au nombre d'individus, mais en moyenne l'erreur est calculée au centième, bien qu'avec des paramètres infructueux, l'erreur peut atteindre des dixièmes
• À l'heure actuelle, une mutation se produit en ajoutant un nombre aléatoire du demi-intervalle au gène

  $$

  $$[-1, 1)$$
  en raison de laquelle les individus ne peuvent pas rester au voisinage de l'extremum et une fluctuation relativement forte se produit dans la distance entre les individus de différentes générations. Dans certains cas, de telles oscillations peuvent être utiles pour sortir d'un extremum local, par exemple, une fonction périodique, mais les extrema peuvent être très éloignés les uns des autres (distance au sens euclidien)
• Dans de nombreux cas, le point extremum est atteint par des individus sur 5 à 15 générations, et les générations restantes «sautent» inutilement au voisinage de cet extremum
• La génération zéro est remplie de nombres aléatoires uniquement dans un carré

  $$

  $$[-1, 1)*[-1, 1)$$
  
  et il peut y avoir des cas où ce carré recouvre un extremum local, ce qui ne nous convient pas

Considérons une surface avec de nombreux extrema de la forme:

$$

$$g(x, y) = \sum\limits_{i=1}^nf_n(h, x_0, y_0), f(h, x_0, y_0) = h*exp(-(x - x_0)^2 - (y - y_0)^2)$$

Les extrema de la fonction g seront aux points

$$

$$(x_0, y_0)$$

.

Test 3

$$

$$g(x, y) = f_1(2, 0, 0) + f_2(5, 3, 3)$$

$$

$$g(x, y) = 2exp(-x^2 - y^2) + 5exp(-(x - 3)^2 - (y - 3)^2)$$

Cet exemple confirme et illustre toutes les observations ci-dessus.

Mise à niveau de l'algorithme génétique

Donc, pour le moment, la fonction de mutation est composée très primitivement: elle ajoute des valeurs aléatoires à partir du demi-intervalle

$$

$$[-1, 1)$$

au gène muté. Une telle invariance de mutation interfère parfois avec le bon fonctionnement de l'algorithme, mais il existe un moyen efficace de corriger ce défaut.

Nous introduisons un nouveau paramètre, que nous appellerons la «plage de mutation» et qui montrera dans quel demi-intervalle le gène mute. Faisons en sorte que ce coefficient de mutation soit inversement proportionnel au nombre de générations. Ceux. plus le nombre de générations est élevé, plus les gènes muteront faibles. Cette solution vous permet de personnaliser la zone de départ et d'améliorer la précision des calculs si nécessaire.

Test 1

$$

$$f(x, y) = sinx$$

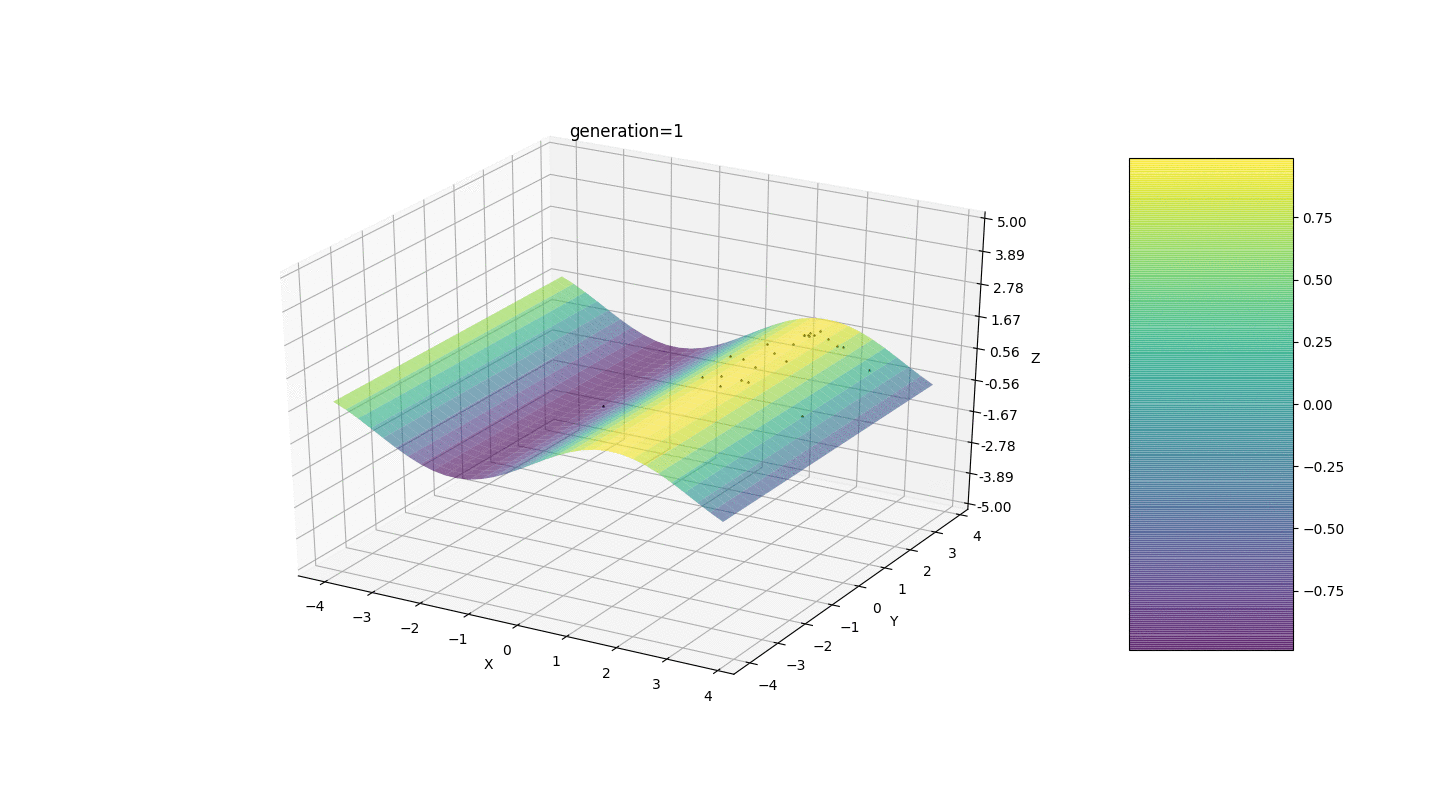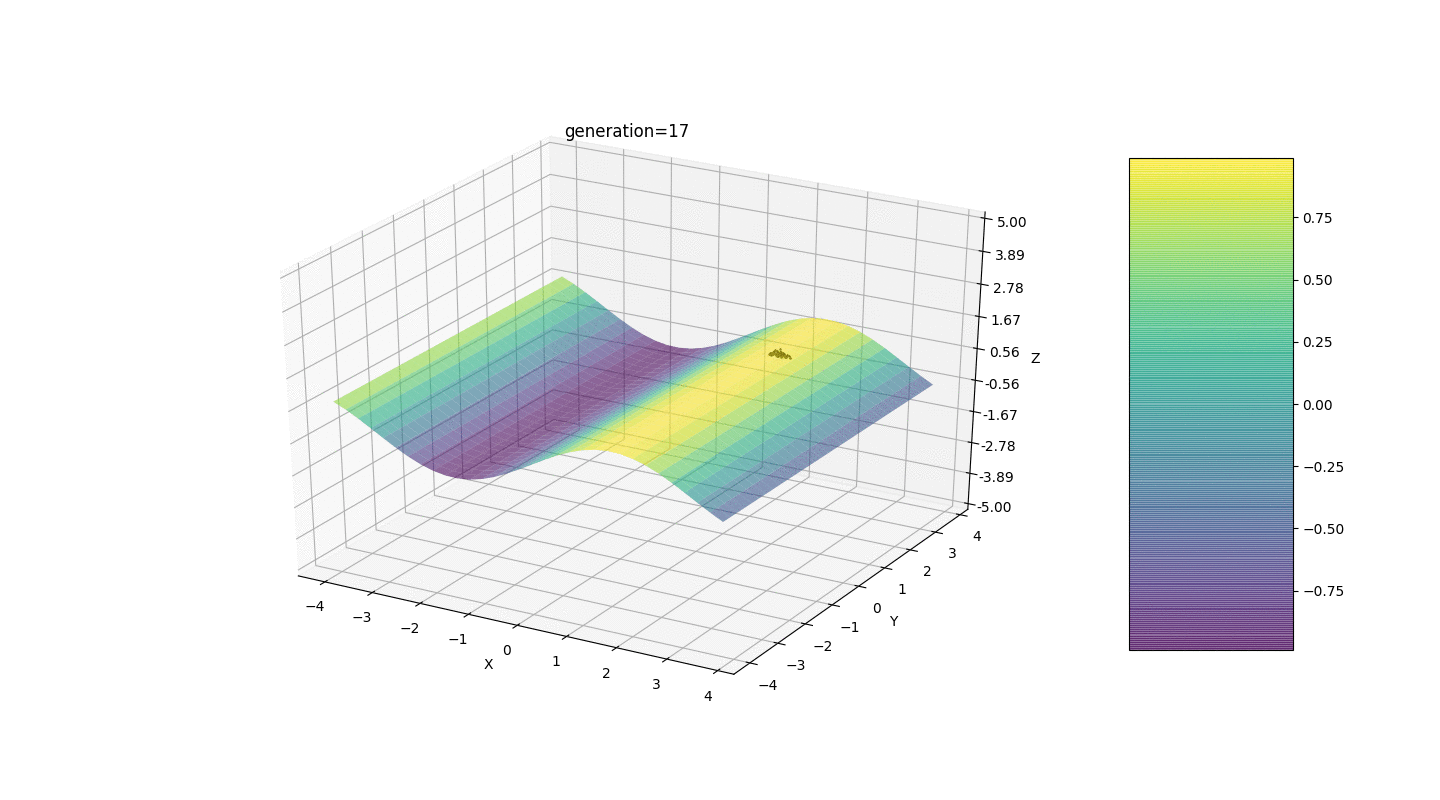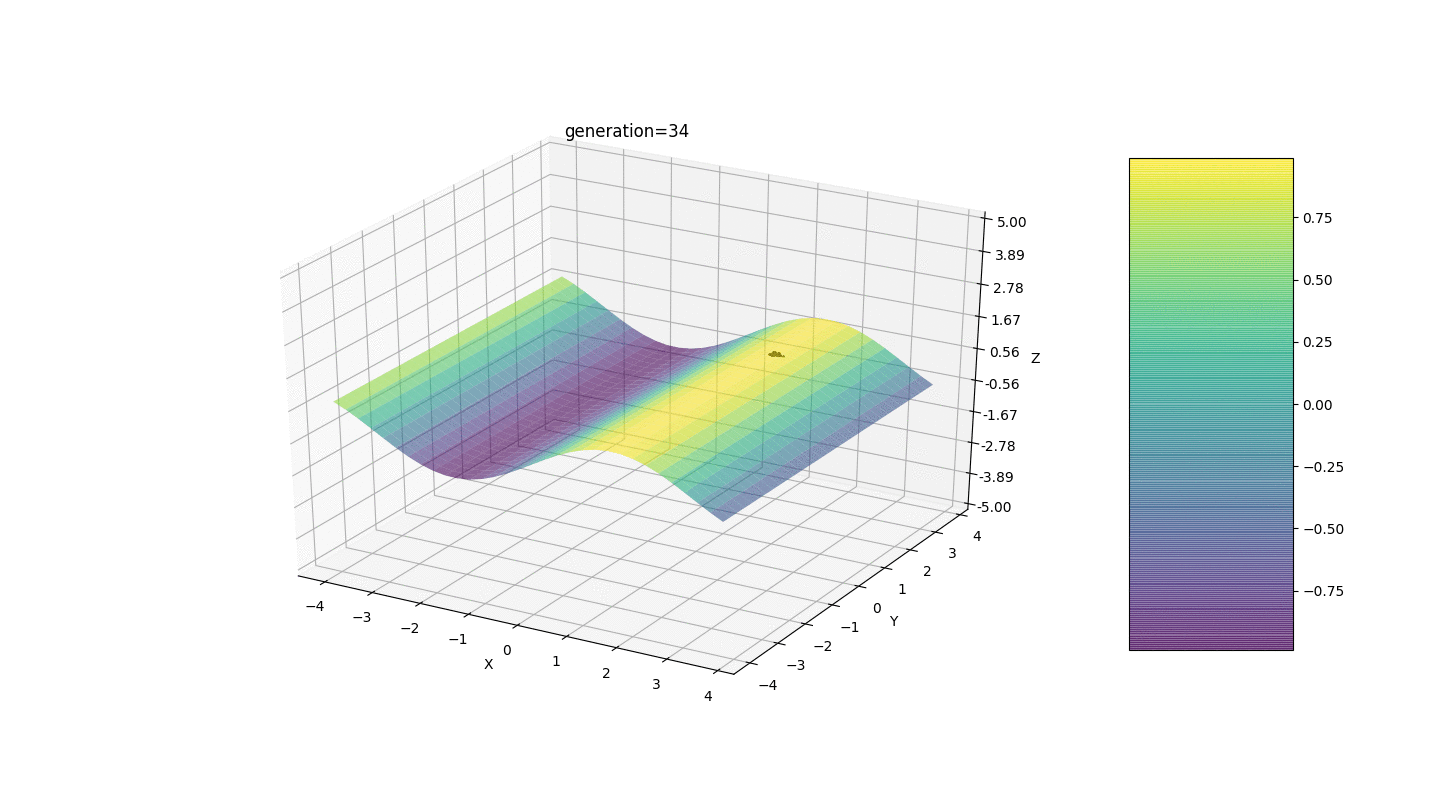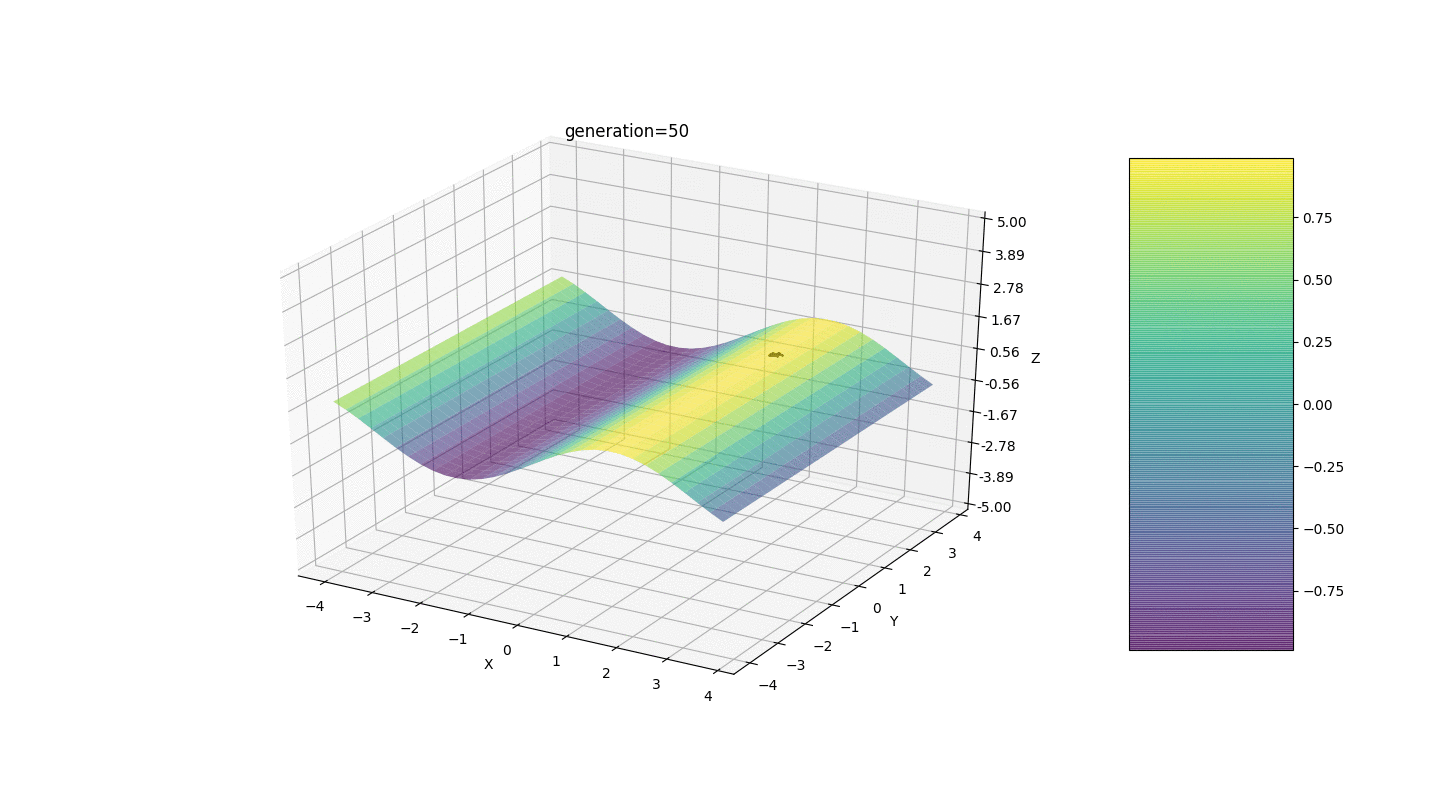
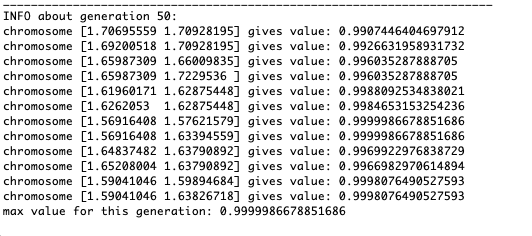Comme le montre l'exemple, maintenant, à chaque génération, la population converge de plus en plus vers un point extremum et calcule les valeurs les plus précises en raison de faibles fluctuations.

Mais qu'en est-il du problème des extrêmes locaux? Prenons un exemple familier.

Test 2

$$

$$g(x, y) = f_1(2, 0, 0) + f_2(5, 3, 3)$$

$$

$$g(x, y) = 2exp(-x^2 - y^2) + 5exp(-(x - 3)^2 - (y - 3)^2)$$

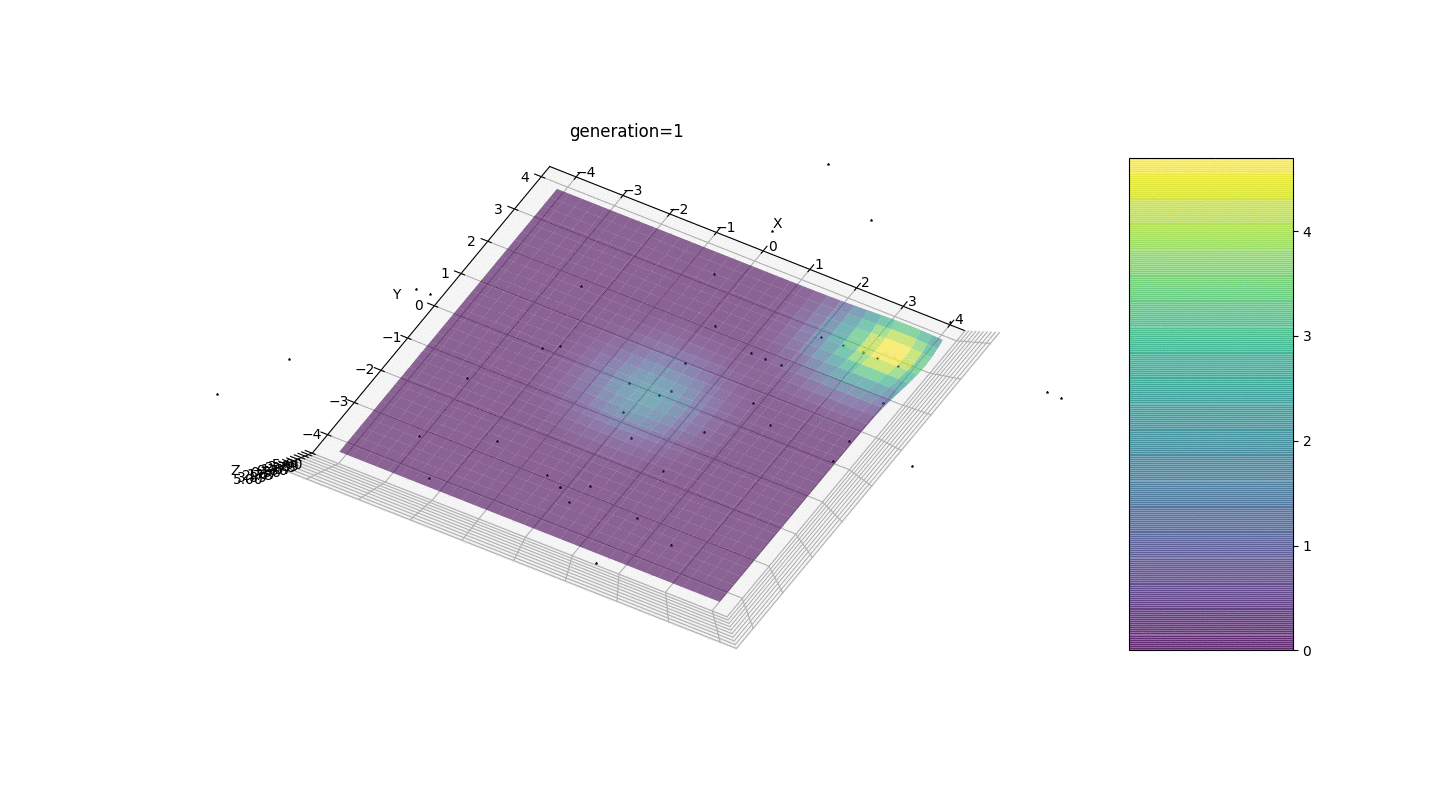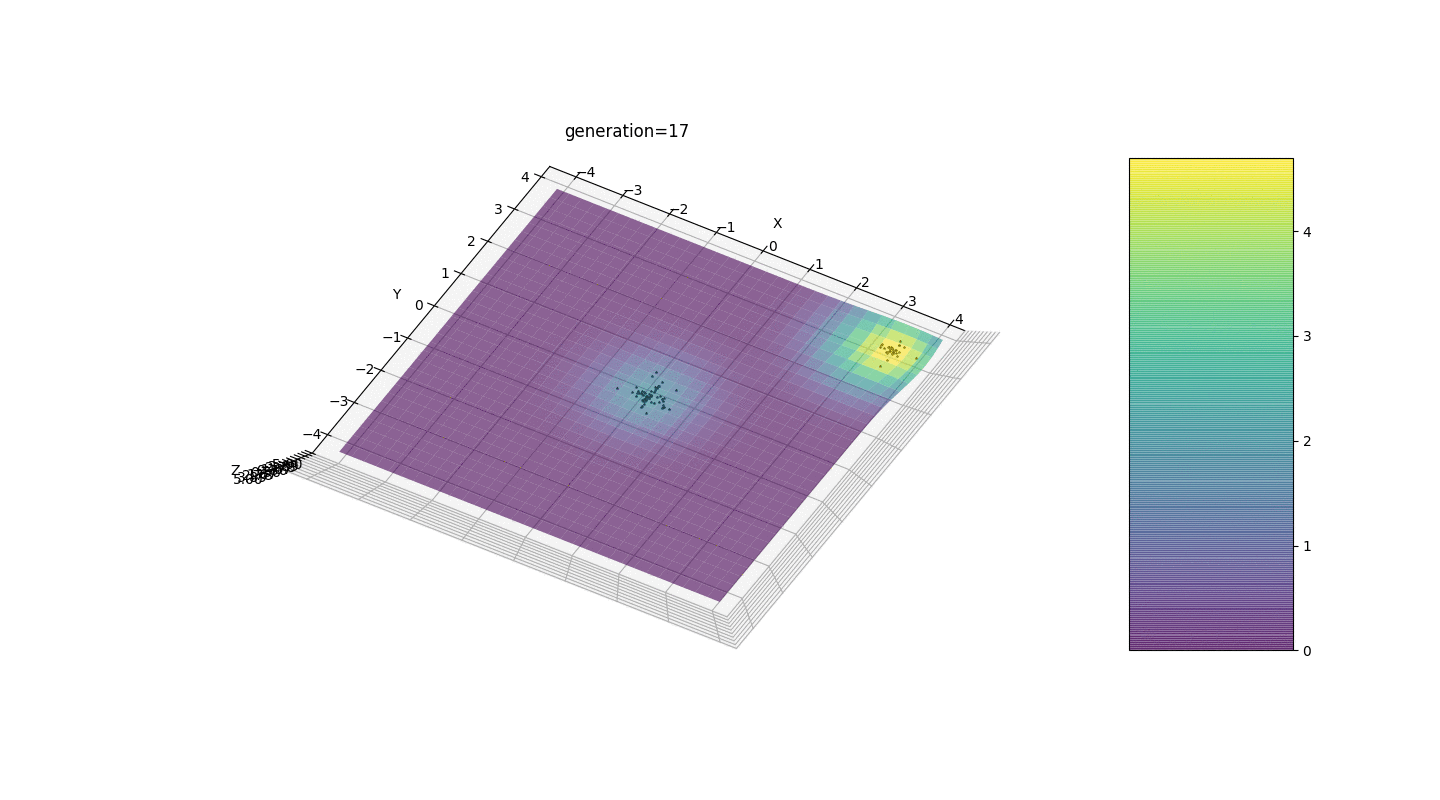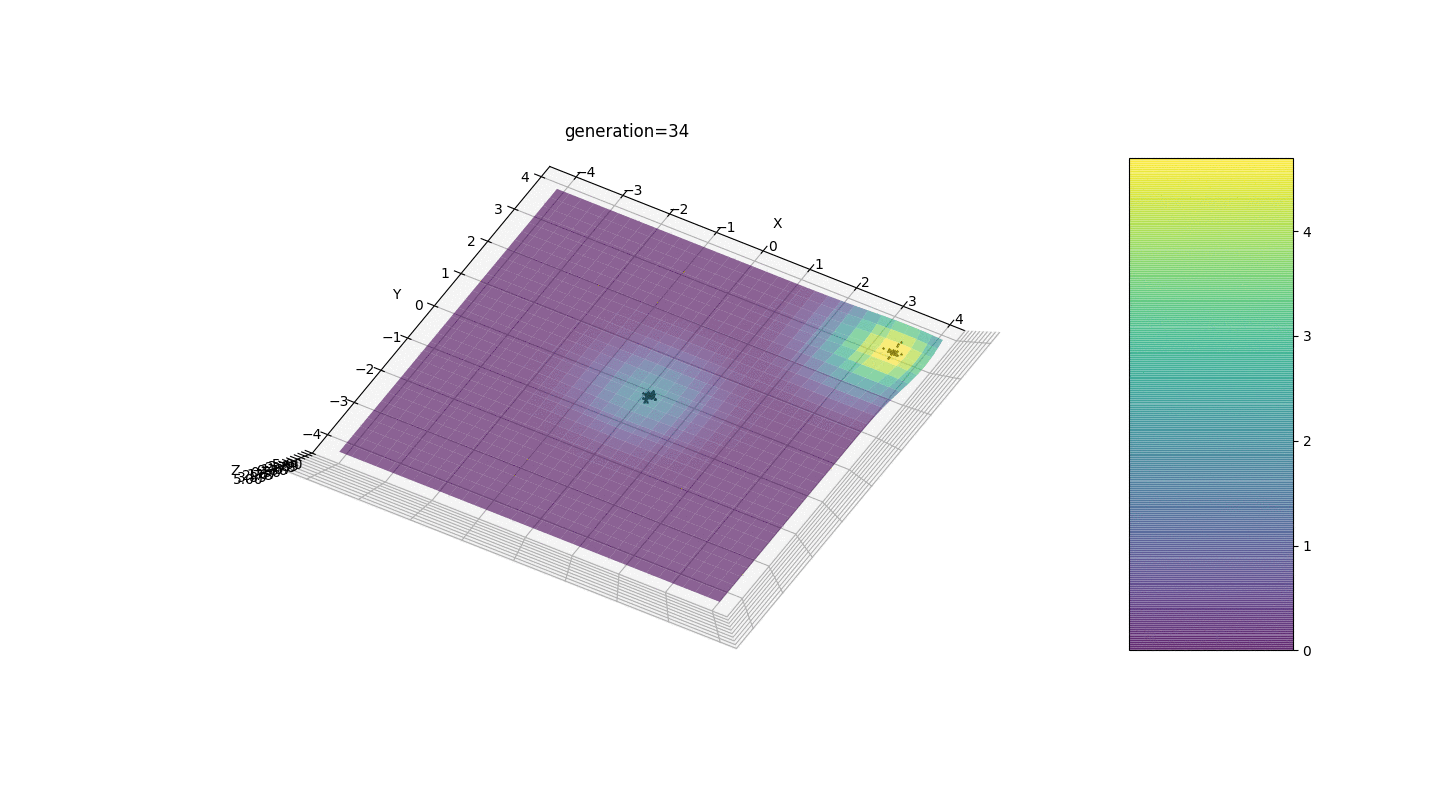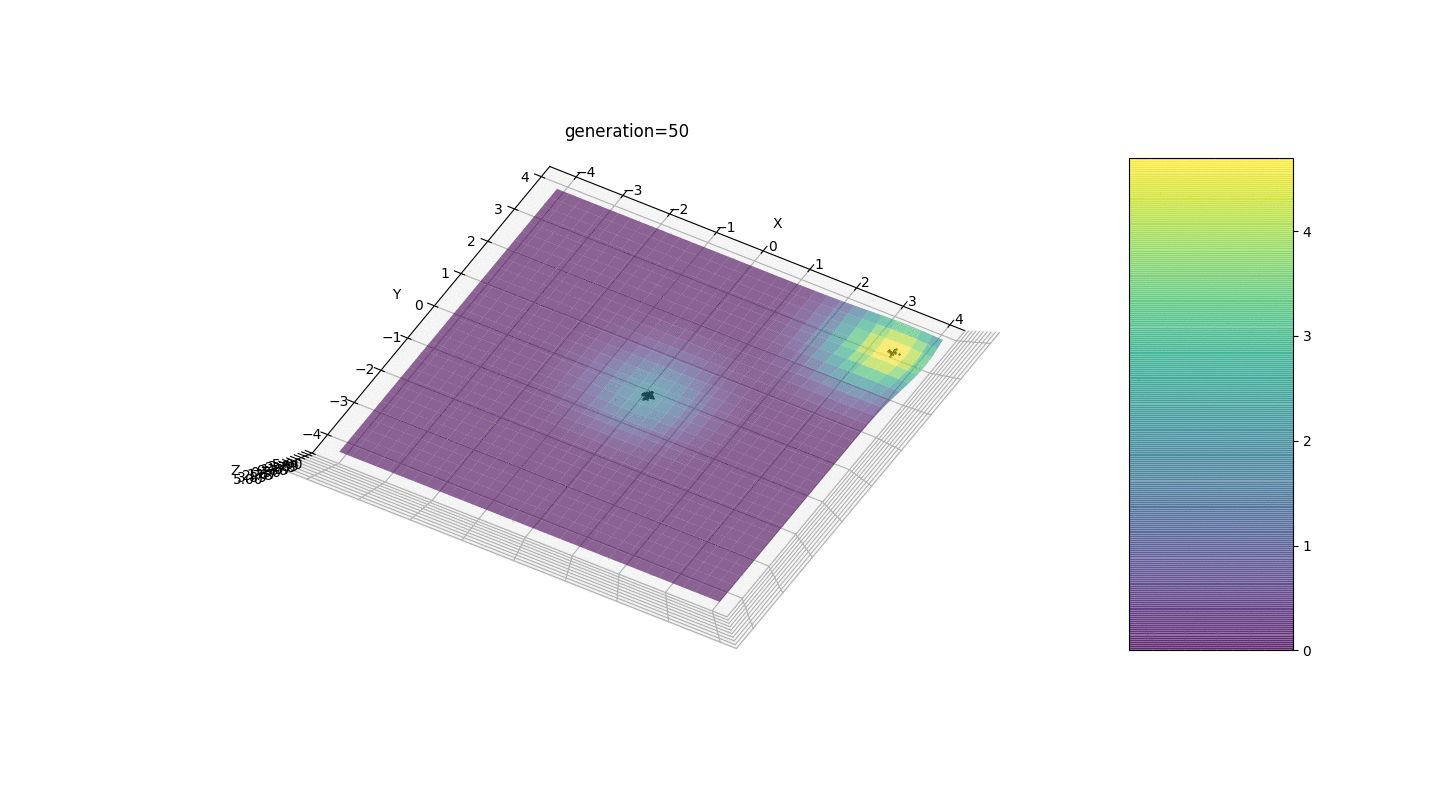
Nous voyons que maintenant l'idée de diviser la population en parties fonctionne comme prévu. Sans cette segmentation, les individus des premières générations pourraient révéler un faux génotype dominant à un extremum local, ce qui conduirait à une réponse incorrecte dans la tâche. On note également une amélioration qualitative de la précision de la réponse en raison de la dépendance introduite de la mutation sur le nombre de générations.

Sommaire

Je résume le résultat:

• ,
• ,

...

• , . , , aka
• Comparaison dans le temps et l'efficacité d'algorithmes similaires avec des méthodes d'optimisation standard, par exemple, descente de gradient
• Nouvelles fonctionnalités du package (probablement)