Dans la partie précédente, nous avons compris comment afficher des objets bidimensionnels, tels qu'un pixel et une ligne (segment), mais vous voulez vraiment créer rapidement quelque chose en trois dimensions. Dans cet article, pour la première fois, nous allons essayer d'afficher un objet 3D à l'écran et de nous familiariser avec de nouveaux objets mathématiques, comme un vecteur et une matrice, ainsi que certaines opérations sur eux, mais uniquement celles qui sont applicables en pratique.Dans la deuxième partie, nous considérerons:- Systèmes de coordonnées
- Point et vecteur
- La matrice
- Sommets et index
- Convoyeur de visualisation
Systèmes de coordonnées
Il convient de noter que certains exemples et opérations dans les articles sont présentés de manière inexacte et grandement simplifiés pour améliorer la compréhension du matériel, en saisissant l'essence, vous pouvez indépendamment trouver la meilleure solution ou corriger les erreurs et les inexactitudes dans le code de démonstration. Avant de dessiner quelque chose en trois dimensions, il est important de se rappeler que tout en trois dimensions sur l'écran est affiché en pixels en deux dimensions. Pour que les objets dessinés par des pixels semblent tridimensionnels, nous devons faire un peu de calcul. Nous ne considérerons pas les formules et les objets sans voir leur application. C'est pourquoi, toutes les opérations mathématiques que vous rencontrerez dans cet article seront mises en pratique, ce qui simplifiera leur compréhension. La première chose à comprendre est le système de coordonnées. Voyons quels systèmes de coordonnées sont utilisés, et choisissons également celui à utiliser pour nous.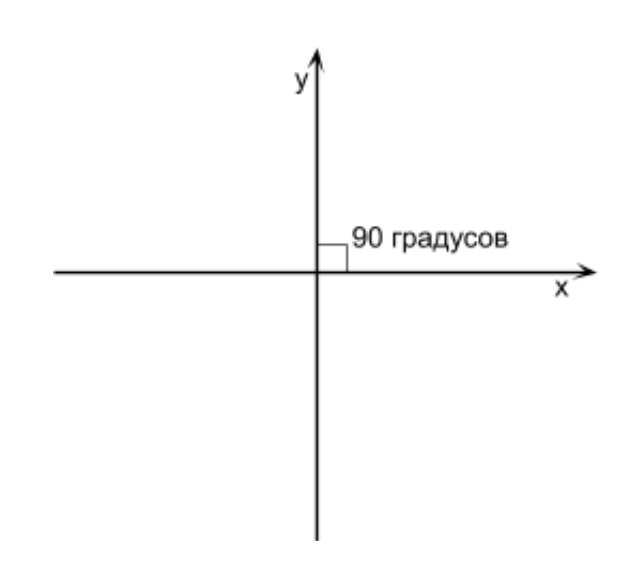
Qu'est-ce qu'un système de coordonnées? C'est un moyen de déterminer la position d'un point ou d'un personnage dans un jeu composé de points à l'aide de chiffres. Le système de coordonnées a 2 directions des axes (nous les désignerons comme X, Y) si nous travaillons avec des graphiques 2D. Si nous définissons un objet 2D avec un Y plus grand et qu'il devient plus élevé qu'auparavant, cela signifie que l'axe Y est vers le haut. Si nous donnons à l'objet un X plus grand et qu'il devient plus à droite, cela signifie que l'axe X est dirigé vers la droite. C'est la direction des axes, et ensemble, ils sont appelés le système de coordonnées. Si un angle de 90 degrés est formé à l'intersection des axes X et Y, alors un tel système de coordonnées est appelé rectangulaire (également appelé système de coordonnées cartésiennes) (voir la figure ci-dessus).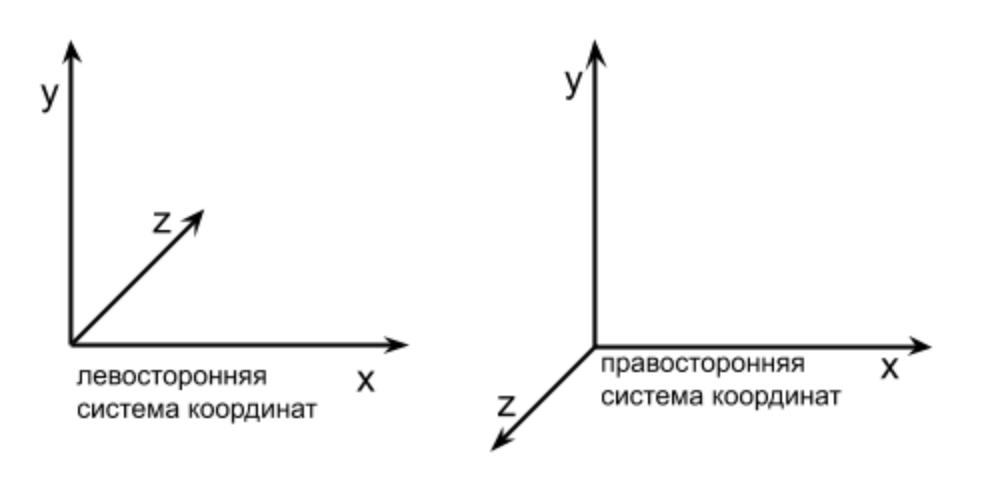
Point et vecteur
Maintenant, vous savez essentiellement ce que sont les systèmes de coordonnées et quelles sont les directions des axes. Ensuite, vous devez analyser ce qu'est un point et un vecteur, car nous en aurons besoin dans cet article pour la pratique. Un point dans l'espace 3D est un emplacement spécifié par [X, Y, Z]. Par exemple, nous voulons placer notre personnage à l'origine même (peut-être au centre de la fenêtre), alors sa position sera [0, 0, 0], ou nous pouvons dire qu'il est situé au point [0, 0, 0]. Maintenant, nous voulons placer l'adversaire à gauche du joueur 20 unités (par exemple, pixels), ce qui signifie qu'il sera situé au point [-20, 0, 0]. Nous travaillerons constamment avec des points, nous les analyserons donc plus en détail plus tard. Qu'est-ce qu'un vecteur? Telle est la direction. Dans l'espace 3D, il est décrit, comme un point, par 3 valeurs [X, Y, Z]. Par exemple, nous devons déplacer le personnage de 5 unités par seconde, nous allons donc changer Y, en y ajoutant 5 chaque seconde, mais nous ne toucherons pas X et Z, ce mouvement peut être écrit comme un vecteur [0, 5, 0]. Si notre personnage descend constamment de 2 unités et vers la droite de 1, alors le vecteur de son mouvement ressemblera à ceci: [1, -2, 0]. Nous avons écrit -2 parce que Y down diminue.Le vecteur n'a pas de position et [X, Y, Z] indiquent la direction. Un vecteur peut être ajouté à un point afin d'obtenir un nouveau point décalé par un vecteur. Par exemple, j'ai déjà mentionné ci-dessus que si nous voulons déplacer un objet 3D (par exemple, un personnage de jeu) toutes les 5 unités vers le haut, le vecteur de déplacement sera comme ceci: [0, 5, 0]. Mais comment l'utiliser pour bouger? Supposons que le caractère soit au point [5, 7, 0] et que le vecteur de déplacement soit [0, 5, 0]. Si nous ajoutons un vecteur au point, nous obtenons une nouvelle position de joueur. Vous pouvez ajouter un point avec un vecteur ou un vecteur avec un vecteur selon la règle suivante.Un exemple d'ajout d'un point et d'un vecteur :[ 5, 7, 0 ] + [ 0, 5, 0 ] = [ 5 + 0, 7 + 5 , 0 + 0 ] = [5, 12, 0] - c'est la nouvelle position de notre personnage. Comme vous pouvez le voir, notre personnage a augmenté de 5 unités, à partir de là, un nouveau concept apparaît - la longueur du vecteur. Chaque vecteur l'a, à l'exception du vecteur [0, 0, 0], qui est appelé le vecteur zéro, un tel vecteur n'a pas non plus de direction. Pour le vecteur [0, 5, 0], la longueur est 5, car un tel vecteur déplace le point de 5 unités vers le haut. Le vecteur [0, 0, 10] a une longueur de 10 car il peut déplacer le point de 10 le long de l'axe Z. Mais le vecteur [12, 3, -4] ne vous dit pas quelle est la longueur, nous allons donc utiliser la formule pour calculer la longueur du vecteur. La question se pose, pourquoi avons-nous besoin de la longueur du vecteur? Une application consiste à savoir jusqu'où le personnage va se déplacer, ou à comparer les vitesses des personnages qui ont un vecteur de déplacement plus long, c'est plus rapide. La longueur est également utilisée pour certaines opérations sur les vecteurs.La longueur du vecteur peut être calculée en utilisant la formule suivante à partir de la première partie (seul Z a été ajouté):
Calculons la longueur du vecteur en utilisant la formule ci-dessus [6, 3, -8];
La longueur du vecteur [6, 3, -8] est d'environ 10,44.Nous savons déjà ce qu'est un point, un vecteur, comment additionner un point et un vecteur (ou 2 vecteurs), et comment calculer la longueur d'un vecteur. Ajoutons une classe vectorielle et implémentons la somme et le calcul de la longueur. Je veux aussi faire attention au fait que nous ne créerons pas de classe pour un point, si nous avons besoin d'un point, alors nous utiliserons la classe vectorielle, car le point et le vecteur stockent X, Y, Z, juste pour le point cette position, et pour le vecteur la direction.Ajoutez la classe vectorielle au projet de l'article précédent, vous pouvez l'ajouter sous la classe Drawer. J'ai appelé Vector ma classe et y ai ajouté 3 propriétés X, Y, Z:class Vector {
x = 0;
y = 0;
z = 0;
constructor(x, y, z) {
this.x = x;
this.y = y;
this.z = z;
}
}
Notez que les champs x, y, z sans les fonctions d '"accesseurs", afin que nous puissions accéder directement aux données dans l'objet, cela se fait pour un accès plus rapide. Plus tard, nous optimiserons encore plus ce code, mais pour l'instant, laissez-le afin d'améliorer la lisibilité.Maintenant, nous implémentons la sommation des vecteurs. La fonction prendra 2 vecteurs sommables, donc je pense à la rendre statique. Le corps de la fonction fonctionnera selon la formule ci-dessus. Le résultat de notre sommation est un nouveau vecteur, avec lequel nous reviendrons:static add(v1, v2) {
return new Vector(
v1.x + v2.x,
v1.y + v2.y,
v1.z + v2.z,
);
}
Reste à implémenter la fonction de calcul de la longueur du vecteur. Encore une fois, nous mettons tout en œuvre selon les formules les plus élevées:getLength() {
return Math.sqrt(
this.x * this.x + this.y * this.y + this.z * this.z
);
}
Examinons maintenant une autre opération sur le vecteur, qui sera nécessaire un peu plus loin dans ce document et beaucoup dans les articles suivants - «normalisation du vecteur». Supposons que nous ayons un personnage dans le jeu que nous déplaçons avec les touches fléchées. Si nous appuyons vers le haut, il se déplace vers le vecteur [0, 1, 0], s'il est vers le bas, puis [0, -1, 0], vers la gauche [-1, 0, 0] et vers la droite [1, 0, 0]. On voit clairement ici que les longueurs de chacun des vecteurs sont 1, c'est-à-dire que la vitesse du personnage est 1. Et ajoutons un mouvement diagonal, si le joueur serre la flèche vers le haut et vers la droite, quel sera le vecteur de déplacement? L'option la plus évidente est le vecteur [1, 1, 0]. Mais si nous calculons sa longueur, nous verrons qu'elle est approximativement égale à 1,414. Il s'avère que notre personnage ira plus vite en diagonale? Cette option ne convient pas, mais pour que notre personnage passe en diagonale à une vitesse de 1, le vecteur doit être:[0,707, 0,707, 0]. Où ai-je obtenu un tel vecteur? J'ai pris le vecteur [1, 1, 0] et l'ai normalisé, après quoi j'ai obtenu [0,707, 0,707, 0]. C'est-à-dire que la normalisation est la réduction d'un vecteur à une longueur de 1 (longueur unitaire) sans changer sa direction. Notez que les vecteurs [0.707, 0.707, 0] et [1, 1, 0] pointent dans la même direction, c'est-à-dire que le personnage se déplacera strictement vers la droite, mais le vecteur [0.707, 0.707, 0] est normalisé et la vitesse du personnage Maintenant, il sera égal à 1, ce qui élimine le bug avec un mouvement diagonal accéléré. Il est toujours recommandé de normaliser le vecteur avant tout calcul afin d'éviter différents types d'erreurs. Voyons comment normaliser un vecteur. Il est nécessaire de diviser chacune de ses composantes (X, Y, Z) par sa longueur. La fonction de trouver la longueur est déjà là, la moitié du travail est fait,nous écrivons maintenant la fonction de normalisation du vecteur (à l'intérieur de la classe Vector):normalize() {
const length = this.getLength();
this.x /= length;
this.y /= length;
this.z /= length;
return this;
}
La méthode de normalisation normalise le vecteur et le renvoie (ceci), ceci est nécessaire pour qu'à l'avenir il soit possible d'utiliser la normalisation dans les expressions.Maintenant que nous savons ce qu'est la normalisation d'un vecteur et que nous savons qu'il est préférable de l'exécuter avant d'utiliser le vecteur, la question se pose. Si la normalisation d'un vecteur est une réduction à une longueur unitaire, c'est-à-dire que la vitesse de déplacement d'un objet (personnage) sera égale à 1, alors comment accélérer le personnage? Par exemple, lorsque vous déplacez un personnage en diagonale vers le haut / droite à une vitesse de 1, son vecteur sera [0,707, 0,707, 0], et quel vecteur le sera si nous voulons déplacer le personnage 6 fois plus vite? Pour ce faire, il existe une opération appelée «multiplier un vecteur par un scalaire». Le scalaire est le nombre habituel par lequel le vecteur est multiplié. Si le scalaire est égal à 6, alors le vecteur deviendra 6 fois plus long, et notre personnage sera 6 fois plus rapide, respectivement. Comment faire une multiplication scalaire? Pour cela, il faut multiplier chaque composante du vecteur par un scalaire. Par exemple, nous résolvons le problème ci-dessus,lorsqu'un caractère se déplaçant vers un vecteur [0.707, 0.707, 0] (vitesse 1) doit être accéléré 6 fois, c'est-à-dire multiplier le vecteur par scalaire 6. La formule pour multiplier le vecteur "V" par scalaire "s" est la suivante:
Dans notre cas, ce sera:- un nouveau vecteur de déplacement dont la longueur est 6.
Il est important de savoir qu'un scalaire positif redimensionne un vecteur sans changer sa direction; si un scalaire est négatif, il redimensionne également un vecteur (augmente sa longueur) mais change en plus la direction du vecteur à l'opposé. Implémentons la fonction demultiplication d'un vecteur par un scalaire dans notre classe Vector:multiplyByScalarmultiplyByScalar(s) {
this.x *= s;
this.y *= s;
this.z *= s;
return this;
}
La matrice
Nous avons trouvé un peu de vecteurs et quelques opérations sur eux qui seront nécessaires dans cet article. Ensuite, vous devez gérer les matrices.On peut dire qu'une matrice est le tableau bidimensionnel le plus courant. C'est juste qu'en programmation ils utilisent le terme «tableau à deux dimensions», et en mathématiques ils utilisent la «matrice». Pourquoi les matrices sont-elles nécessaires dans la programmation 3D? Nous analyserons cela dès que nous apprendrons à travailler un peu avec eux. Nous n'utiliserons que des matrices numériques (un tableau de nombres). Chaque matrice a sa propre taille (comme tout tableau bidimensionnel). Voici quelques exemples de matrices:De toutes les opérations sur les matrices, nous considérons maintenant uniquement la multiplication (le reste plus tard). Il s'avère que la multiplication matricielle n'est pas l'opération la plus simple, elle peut facilement être déroutante si vous ne suivez pas attentivement l'ordre de multiplication. Mais ne vous inquiétez pas, vous réussirez, car ici, nous ne ferons que multiplier et résumer. Pour commencer, nous devons nous souvenir de quelques fonctionnalités de multiplication dont nous avons besoin:- Si nous essayons de multiplier le nombre A par le nombre B, alors c'est la même chose que B * A. Si nous réorganisons les opérandes et que le résultat ne change sous aucune action, alors ils disent que l'opération est commutative. Exemple: a + b = b + a l'opération est commutative, a - b ≠ b - a l'opération n'est pas commutative, a * b = b * a l'opération de multiplication des nombres est commutative. Ainsi, l'opération de multiplication matricielle est non commutative, contrairement à la multiplication des nombres. Autrement dit, la multiplication de la matrice M par la matrice N ne sera pas égale à la multiplication de la matrice N par M.
- La multiplication matricielle est possible si le nombre de colonnes de la première matrice (qui se trouve à gauche) est égal au nombre de lignes de la deuxième matrice (qui se trouve à droite).
Nous allons maintenant examiner la deuxième caractéristique de la multiplication matricielle (lorsque la multiplication est possible). Voici quelques exemples qui montrent quand la multiplication est possible ou non:Je pense que ces exemples ont un peu clarifié le tableau lorsque la multiplication est possible. Le résultat de la multiplication matricielle sera toujours une matrice dont le nombre de lignes sera égal au nombre de lignes de la 1ère matrice et le nombre de colonnes est égal au nombre de colonnes de la 2ème. Par exemple, si nous multiplions la matrice 2 par 6 et 6 par 8, nous obtenons une matrice de taille 2 par 8. Maintenant, nous allons directement à la multiplication elle-même.Pour la multiplication, il est important de se rappeler que les colonnes et les lignes de la matrice sont numérotées à partir de 1 et dans le tableau à partir de 0. Le premier index de l'élément de matrice indique le numéro de ligne et le second le numéro de colonne. Autrement dit, si l'élément de matrice (élément de tableau) s'écrit: m28, cela signifie que nous passons à la deuxième ligne et à la huitième colonne. Mais puisque nous travaillerons avec des tableaux dans le code, toute l'indexation des lignes et des colonnes commencera à 0.Essayons de multiplier 2 matrices A et B avec des tailles et des éléments spécifiques:
On peut voir que la matrice A a une taille de 3 par 2, et la matrice B a une taille de 2 par 2, la multiplication est possible:
Comme vous pouvez le voir, nous avons une matrice 3 par 2, la multiplication est initialement déroutante, mais s'il y a un objectif d'apprendre à se multiplier «sans stress», plusieurs exemples doivent être résolus. Voici un autre exemple de multiplication des matrices A et B:
Si la multiplication n'est pas complètement claire, alors ça va, car nous n'avons pas à multiplier par feuille. Nous écrirons une fois la fonction de multiplication matricielle et nous l'utiliserons. En général, toutes ces fonctions sont déjà écrites, mais nous faisons tout par nous-mêmes.Maintenant, quelques termes supplémentaires qui seront utilisés à l'avenir:- Une matrice carrée est une matrice dont le nombre de lignes est égal au nombre de colonnes, voici un exemple de matrices carrées:
- La diagonale principale d'une matrice carrée est appelée tous les éléments de la matrice dont le numéro de ligne est égal au numéro de colonne. Exemples de diagonales (dans cet exemple, la diagonale principale est remplie de neuf):
- Une matrice unitaire est une matrice carrée dans laquelle tous les éléments de la diagonale principale sont 1 et tous les autres sont 0. Exemples de matrices unitaires:
Il est également important de se rappeler cette propriété que si nous multiplions une matrice M par une matrice unitaire de taille appropriée, par exemple, appelons-la I, nous obtenons la matrice d'origine M, par exemple: M * I = M ou I * M = M. la multiplication de la matrice par la matrice d'identité n'affecte pas le résultat. Nous reviendrons sur la matrice d'identité plus tard. En programmation 3D, nous utiliserons souvent une matrice carrée 4 x 4.Voyons maintenant pourquoi nous aurons besoin de matrices et pourquoi les multiplier? En programmation 3D, il existe de nombreuses matrices 4 x 4 différentes qui, si elles sont multipliées par un vecteur ou un point, effectueront les actions dont nous avons besoin. Par exemple, nous devons faire pivoter le personnage dans un espace tridimensionnel autour de l'axe X, comment faire? Multipliez le vecteur par une matrice spéciale, qui est responsable de la rotation autour de l'axe X. Si vous devez déplacer et faire pivoter un point autour de l'origine, vous devez multiplier ce point par une matrice spéciale. Les matrices ont une excellente propriété - combinant des transformations (nous allons les considérer dans cet article). Supposons que nous ayons besoin d'un caractère composé de 100 points (sommets, mais ce sera également un peu plus bas) dans l'application, augmentez 5 fois, puis faites pivoter de 90 degrés X, puis déplacez-le de 30 unités.Comme déjà mentionné, pour différentes actions, il existe déjà des matrices spéciales que nous considérerons. Pour accomplir la tâche ci-dessus, nous, par exemple, parcourons les 100 points et chaque premier nous multiplions par la 1ère matrice pour augmenter le caractère, puis nous multiplions par la 2ème matrice pour faire une rotation de 90 degrés en X, puis nous multiplions par 3 e pour déplacer 30 unités vers le haut. Au total, pour chaque point, nous avons 3 multiplications matricielles et 100 points, ce qui signifie qu'il y aura 300 multiplications. Mais si nous prenons et multiplions les matrices entre nous pour augmenter de 5 fois, tourner de 90 degrés le long de X et nous déplacer de 30 unités. up, nous obtenons une matrice qui contient toutes ces actions. En multipliant un point par une telle matrice, le point sera là où il est nécessaire. Calculons maintenant combien d'actions sont effectuées: 2 multiplications pour 3 matrices, et 100 multiplications pour 100 points,un total de 102 multiplications est certainement mieux que 300 multiplications avant cela. Le moment où nous avons multiplié 3 matrices pour combiner différentes actions en une seule matrice - est appelé une combinaison de transformations et nous le ferons certainement avec un exemple.Comment multiplier la matrice par la matrice, nous avons examiné, mais le paragraphe lu ci-dessus parle de la multiplication de la matrice par un point ou un vecteur. Pour multiplier un point ou un vecteur, il suffit de les représenter comme une matrice.Par exemple, nous avons un vecteur [10, 2, 5] et il y a une matrice:
On voit que le vecteur peut être représenté par une matrice de 1 par 3 ou par une matrice de 3 par 1. On peut donc multiplier le vecteur par une matrice de 2 voies:Comme vous pouvez le voir, nous pouvons représenter le vecteur comme un vecteur ligne et le multiplier par une matrice, ou représenter le vecteur comme un vecteur colonne et multiplier la matrice par lui. Vérifions si le résultat de la multiplication sera le même dans les deux cas:Multipliez le vecteur ligne par la matrice:
Maintenant, multipliez la matrice par le vecteur colonne:
Nous voyons qu'en multipliant le vecteur ligne par la matrice et la matrice par le vecteur colonne, nous avons obtenu des résultats complètement différents (nous rappelons la commutativité). Par conséquent, dans la programmation 3D, il existe des matrices conçues pour être multipliées uniquement par un vecteur ligne ou uniquement par un vecteur colonne. Si nous multiplions la matrice destinée au vecteur ligne par le vecteur colonne, nous obtenons un résultat qui ne nous donnera rien. Utilisez la représentation vectorielle / ponctuelle qui vous convient (ligne ou colonne), seulement à l'avenir, utilisez les matrices appropriées pour votre représentation vectorielle / ponctuelle. Direct3D, par exemple, utilise une représentation sous forme de chaîne de vecteurs, et toutes les matrices dans Direct3D sont conçues pour multiplier un vecteur ligne par une matrice. OpenGL utilise une représentation d'un vecteur (ou point) comme une colonne,et toutes les matrices sont conçues pour multiplier la matrice par un vecteur de colonne. Dans les articles, nous utiliserons le vecteur colonne et multiplierons la matrice par le vecteur colonne.Pour résumer ce que nous lisons sur la matrice.- Pour effectuer une action sur un vecteur (ou point), il existe des matrices spéciales, dont certaines seront présentées dans cet article.
- Pour combiner la transformation (déplacement, rotation, etc.), nous pouvons multiplier les matrices de chaque transformation entre elles et obtenir une matrice qui contient toutes les transformations ensemble.
- En programmation 3D, nous utiliserons constamment des matrices carrées de 4 x 4.
- Nous pouvons multiplier la matrice par un vecteur (ou point) en la représentant sous forme de colonne ou de ligne. Mais pour le vecteur de colonne et le vecteur de ligne, vous devez utiliser différentes matrices.
Après une petite analyse des matrices, ajoutons une classe de matrice 4 x 4 et implémentons des méthodes pour multiplier la matrice par la matrice et le vecteur par la matrice. Nous utiliserons la taille de la matrice 4 par 4, car toutes les matrices standard qui sont utilisées pour diverses actions (mouvement, rotation, échelle, ...) sont d'une telle taille, nous n'avons pas besoin de matrices d'une taille différente. Ajoutons la classe Matrix au projet. Parfois, la classe pour travailler avec des matrices 4 x 4 est appelée Matrix4, et ce 4 dans le titre nous renseigne sur la taille de la matrice (ils disent aussi la matrice de 4e ordre). Toutes les données de la matrice seront stockées dans un tableau bidimensionnel 4 x 4.Nous passons à la mise en place d'opérations de multiplication. Je ne recommande pas d'utiliser des boucles pour cela. Pour améliorer les performances, nous devons tous multiplier ligne par ligne - cela se produira car toutes les multiplications se produiront avec des matrices de taille fixe. J'utiliserai des cycles pour l'opération de multiplication, seulement pour économiser la quantité de code, vous pouvez écrire toute la multiplication sans cycles du tout. Mon code de multiplication ressemble à ceci:class Matrix {
static multiply(a, b) {
const m = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
];
for (let i = 0; i < 4; i++) {
for (let j = 0; j < 4; j++) {
m[i][j] = a[i][0] * b[0][j] +
a[i][1] * b[1][j] +
a[i][2] * b[2][j] +
a[i][3] * b[3][j];
}
}
return m;
}
}
Comme vous pouvez le voir, la méthode prend les matrices a et b, les multiplie et retourne le résultat dans le même tableau 4 par 4. Au début de la méthode, j'ai créé une matrice m remplie de zéros, mais ce n'est pas nécessaire, donc je voulais montrer de quelle dimension sera le résultat, vous Vous pouvez créer un tableau 4 x 4 sans aucune donnée.Vous devez maintenant implémenter la multiplication de la matrice par le vecteur colonne, comme expliqué ci-dessus. Mais si vous représentez le vecteur comme une colonne, vous obtenez une matrice de la forme:par lequel nous devrons multiplier par 4 par 4 matrices pour effectuer diverses actions. Mais dans cet exemple, on voit clairement qu'une telle multiplication ne peut pas être effectuée, car le vecteur de colonne a 3 lignes et la matrice a 4 colonnes. Que faire alors? Un quatrième élément est nécessaire, alors le vecteur aura 4 lignes, qui seront égales au nombre de colonnes dans la matrice. Ajoutons un tel 4ème paramètre au vecteur et appelons-le W, maintenant nous avons tous les vecteurs 3D sous la forme [X, Y, Z, W] et ces vecteurs peuvent déjà être multipliés par 4 par 4. En fait, le composant W un but plus profond, mais nous apprendrons à le connaître dans la partie suivante (ce n'est pas pour rien que nous avons une matrice 4 x 4, pas 3 x 3). Ajoutez à la classe Vector, que nous avons créée au-dessus du composant w. Maintenant, le début de la classe Vector ressemble à ceci:class Vector {
x = 0;
y = 0;
z = 0;
w = 1;
constructor(x, y, z, w = 1) {
this.x = x;
this.y = y;
this.z = z;
this.w = w;
}
J'ai initialisé W à un, mais pourquoi 1? Si nous regardons comment les composants de la matrice et du vecteur sont multipliés (l'exemple de code ci-dessous), vous pouvez voir que si vous définissez W à 0 ou toute autre valeur autre que 1, alors lorsque vous multipliez ce W affectera le résultat, mais nous ne le faisons pas nous savons comment l'utiliser, et si nous le faisons 1, alors il sera dans le vecteur, mais le résultat ne changera en aucune façon. Revenons maintenant à la matrice et implémentons dans la classe Matrix (vous pouvez aussi dans la classe Vector, il n'y a pas de différence) la matrice est multipliée par un vecteur, ce qui est déjà possible, grâce à W:static multiplyVector(m, v) {
return new Vector(
m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
)
}
Veuillez noter que nous avons présenté la matrice comme un tableau 4 x 4 et le vecteur comme un objet avec les propriétés x, y, z, w, à l'avenir, nous changerons le vecteur et il sera également représenté par un tableau 1 x 4, car cela accélérera la multiplication. Mais maintenant, pour mieux voir comment la multiplication se produit et améliorer la compréhension du code, nous ne changerons pas le vecteur.Nous avons écrit le code pour la multiplication matricielle entre nous et la multiplication matrice-vecteur, mais on ne sait toujours pas comment cela nous aidera dans les graphiques en trois dimensions.Je veux également vous rappeler que j'appelle un vecteur à la fois un point (position dans l'espace) et une direction, car les deux objets contiennent la même structure de données x, y, z et le nouveau w. Examinons quelques-unes des matrices qui effectuent des opérations de base sur des vecteurs. La première de ces matrices sera la matrice de traduction. En multipliant la matrice de déplacement par un vecteur (emplacement), elle se décalera du nombre spécifié d'unités dans l'espace. Et voici la matrice de déplacement:
Lorsque dx, dy, dz signifient des déplacements le long des axes x, y, z, respectivement, cette matrice est conçue pour être multipliée par un vecteur de colonne. De telles matrices peuvent être trouvées sur Internet ou dans toute littérature sur la programmation 3D, nous n'avons pas besoin de les créer nous-mêmes, prenez-les maintenant, comme les formules que vous utilisez de l'école dont vous avez juste besoin de savoir ou de comprendre pourquoi les utiliser. Vérifions si, en effet, en multipliant une telle matrice par un vecteur, un décalage se produira. Prenons comme vecteur on va déplacer le vecteur [10, 10, 10, 1] (on laisse toujours le 4ème paramètre W toujours 1), supposons que c'est la position de notre personnage dans le jeu et on veut le décaler de 10 unités vers le haut, 5 unités à droite et à 1 unité de l'écran. Alors le vecteur de déplacement sera comme ceci [10, 5, -1] (-1 parce que nous avons un système de coordonnées droitier et le Z supplémentaire,plus il est petit). Si nous calculons le résultat sans matrices, par la somme habituelle des vecteurs. Cela se traduira par le résultat suivant: [10 + 10, 10 + 5, 10 + -1, 1] = [20, 15, 9, 1] - ce sont les nouvelles coordonnées de notre personnage. En multipliant la matrice ci-dessus par les coordonnées initiales [10, 10, 10, 1], nous devrions obtenir le même résultat, vérifions cela dans le code, écrivons la multiplication après les classes Drawer, Vector et Matrix:const translationMatrix = [
[1, 0, 0, 10],
[0, 1, 0, 5],
[0, 0, 1, -1],
[0, 0, 0, 1],
]
const characterPosition = new Vector(10, 10, 10)
const newCharacterPosition = Matrix.multiplyVector(
translationMatrix, characterPosition
)
console.log(newCharacterPosition)
Dans cet exemple, nous avons substitué le décalage de caractère souhaité (translationMatrix) dans la matrice de déplacement, initialisé sa position initiale (characterPosition), puis multiplié avec la matrice, et le résultat a été généré via console.log (il s'agit de la sortie de débogage dans JS). Si vous utilisez du non-JS, alors sortez vous-même X, Y, Z en utilisant les outils de votre langue. Le résultat que nous avons obtenu dans la console: [20, 15, 9, 1], tout concorde avec le résultat que nous avons calculé ci-dessus. Vous pouvez avoir une question, pourquoi obtenir le même résultat en multipliant le vecteur par une matrice spéciale, si nous l'avons obtenu beaucoup plus facilement en additionnant le vecteur avec un décalage par composant. La réponse n'est pas la plus simple et nous allons en discuter plus en détail, mais maintenant on peut noter que, comme discuté précédemment, nous pouvons combiner des matrices avec différentes transformations entre elles,réduisant ainsi autant de calculs. Dans l'exemple ci-dessus, nous avons créé la matrice translationMatrix manuellement et y avons substitué le décalage nécessaire, mais comme nous utiliserons souvent ceci et d'autres matrices, plaçons-le dans une méthode de la classe Matrix et transmettons le décalage avec des arguments:static getTranslation(dx, dy, dz) {
return [
[1, 0, 0, dx],
[0, 1, 0, dy],
[0, 0, 1, dz],
[0, 0, 0, 1],
]
}
Regardez de plus près la matrice de déplacement, vous verrez que dx, dy, dz sont dans la dernière colonne, et si nous regardons le code pour multiplier la matrice par un vecteur, nous remarquerons que cette colonne est multipliée par la composante W du vecteur. Et si c'était, par exemple, 0, alors dx, dy, dz, nous multiplierions par 0 et le mouvement ne fonctionnerait pas. Mais nous pouvons faire W égal à 0 si nous voulons stocker la direction dans la classe Vector, car il est impossible de déplacer la direction, donc nous nous protégerions, et même si nous multiplions une telle direction par la matrice de déplacement, cela ne cassera pas le vecteur direction, car tout mouvement sera multiplié par 0. Autotal, nous pouvons appliquer une telle règle, nous créons un emplacement comme celui-ci:new Vector(x, y, z, 1)
Et nous allons créer la direction comme ceci:new Vector(x, y, z, 0)
Ainsi, nous pouvons distinguer l'emplacement et la direction, et lorsque nous multiplions la direction par la matrice de déplacement, nous ne casserons pas accidentellement le vecteur de direction.Sommets et index
Avant de voir ce que sont les autres matrices, nous verrons un peu comment appliquer nos connaissances existantes pour afficher quelque chose en trois dimensions à l'écran. Tout ce que nous avons déduit auparavant, ce sont les lignes et les pixels. Mais utilisons maintenant ces outils pour dériver, par exemple, un cube. Pour ce faire, nous devons comprendre en quoi consiste un modèle tridimensionnel. La composante la plus fondamentale de tout modèle 3D est les points (nous appellerons les sommets ci-dessous) le long desquels nous pouvons les dessiner; ce sont, en fait, beaucoup de vecteurs de localisation, qui, si nous les connectons correctement avec des lignes, nous obtenons un modèle 3D (grille de modèle ) à l'écran, ce sera sans texture et sans beaucoup d'autres propriétés, mais tout a son temps. Jetez un oeil au cube que nous voulons sortir et essayez de comprendre combien de sommets il a: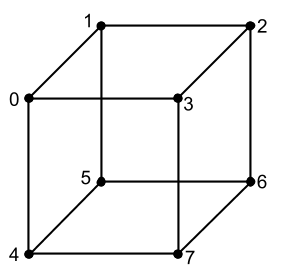
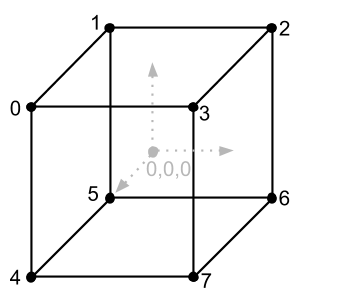
const vertices = [
new Vector(-1, 1, 1),
new Vector(-1, 1, -1),
new Vector(1, 1, -1),
new Vector(1, 1, 1),
new Vector(-1, -1, 1),
new Vector(-1, -1, -1),
new Vector(1, -1, -1),
new Vector(1, -1, 1),
];
Je mets chaque sommet dans une instance de la classe Vector, ce n'est pas la meilleure option pour les performances (mieux dans un tableau), mais maintenant notre objectif est de comprendre comment tout fonctionne.Prenons maintenant les coordonnées des sommets du cube comme pixels que nous allons dessiner sur l'écran, dans ce cas, nous voyons que la taille du cube est de 2 x 2 x 2 pixels. Nous avons créé un si petit cube pour que regardez le travail de la matrice de mise à l'échelle, avec laquelle nous allons l'augmenter. À l'avenir, il est très pratique de faire des modèles petits, voire plus petits que les nôtres, afin de les augmenter à la taille souhaitée avec des scalaires peu différents.C'est juste que dessiner des points de cube avec des pixels n'est pas très clair, car tout ce que nous voyons est de 8 pixels, un pour chaque sommet, il est préférable de dessiner un cube avec des lignes en utilisant la fonction drawLine de l'article précédent. Mais pour cela, nous devons comprendre de quels sommets à quelles lignes nous passons. Revoyons l'image du cube avec les indices et nous verrons qu'il est composé de 12 lignes (ou bords). Il est également très facile de voir que nous connaissons les coordonnées du début et de la fin de chaque ligne. Par exemple, l'une des lignes (supérieure proche) doit être dessinée du sommet 0 au sommet 3, ou des coordonnées [-1, 1, 1] aux coordonnées [1, 1, 1]. Nous devrons écrire des informations sur chaque ligne du code en regardant manuellement l'image du cube, mais comment le faire correctement? Si nous avons 12 lignes et chaque ligne a un début et une fin, c'est-à-dire 2 points, alors,pour dessiner un cube, nous avons besoin de 24 points? C'est la bonne réponse, mais regardons à nouveau l'image du cube et faisons attention au fait que chaque ligne du cube a des sommets communs, par exemple, au sommet 0, 3 lignes sont connectées, et donc avec chaque sommet. Nous pouvons économiser de la mémoire et ne pas écrire les coordonnées du début et de la fin de chaque ligne, il suffit de créer un tableau et de spécifier les indices de sommet à partir du tableau de sommets dans lequel ces lignes commencent et se terminent. Créons un tel tableau et décrivons-le uniquement avec des index de vertex, 2 index par ligne (le début de la ligne et la fin). Et un peu plus loin, lorsque nous dessinons ces lignes, nous pouvons facilement obtenir leurs coordonnées à partir du tableau de sommets. Mon tableau de lignes (je l'ai appelé bords, car ce sont les bords du cube) J'ai créé un tableau de sommets ci-dessous et il ressemble à ceci:mais regardons à nouveau l'image du cube et faisons attention au fait que chaque ligne du cube a des sommets communs, par exemple, au sommet 0 3 lignes sont connectées, et donc à chaque sommet. Nous pouvons économiser de la mémoire et ne pas écrire les coordonnées du début et de la fin de chaque ligne, il suffit de créer un tableau et de spécifier les indices de sommet à partir du tableau de sommets dans lequel ces lignes commencent et se terminent. Créons un tel tableau et décrivons-le uniquement avec des index de vertex, 2 index par ligne (le début de la ligne et la fin). Et un peu plus loin, lorsque nous dessinons ces lignes, nous pouvons facilement obtenir leurs coordonnées à partir du tableau de sommets. Mon tableau de lignes (je l'ai appelé bords, car ce sont les bords du cube) J'ai créé un tableau de sommets ci-dessous et il ressemble à ceci:mais regardons à nouveau l'image du cube et faisons attention au fait que chaque ligne du cube a des sommets communs, par exemple, au sommet 0 3 lignes sont connectées, et donc à chaque sommet. Nous pouvons économiser de la mémoire et ne pas écrire les coordonnées du début et de la fin de chaque ligne, il suffit de créer un tableau et de spécifier les indices de sommet à partir du tableau de sommets dans lequel ces lignes commencent et se terminent. Créons un tel tableau et décrivons-le uniquement avec des index de vertex, 2 index par ligne (le début de la ligne et la fin). Et un peu plus loin, lorsque nous dessinons ces lignes, nous pouvons facilement obtenir leurs coordonnées à partir du tableau de sommets. Mon tableau de lignes (je l'ai appelé bords, car ce sont les bords du cube) J'ai créé un tableau de sommets ci-dessous et il ressemble à ceci:et ainsi avec chaque sommet. Nous pouvons économiser de la mémoire et ne pas écrire les coordonnées du début et de la fin de chaque ligne, il suffit de créer un tableau et de spécifier les indices de sommet à partir du tableau de sommets dans lequel ces lignes commencent et se terminent. Créons un tel tableau et décrivons-le uniquement avec des index de vertex, 2 index par ligne (le début de la ligne et la fin). Et un peu plus loin, lorsque nous dessinons ces lignes, nous pouvons facilement obtenir leurs coordonnées à partir du tableau de sommets. Mon tableau de lignes (je l'ai appelé bords, car ce sont les bords du cube) J'ai créé un tableau de sommets ci-dessous et il ressemble à ceci:et ainsi avec chaque sommet. Nous pouvons économiser de la mémoire et ne pas écrire les coordonnées du début et de la fin de chaque ligne, il suffit de créer un tableau et de spécifier les indices de sommet à partir du tableau de sommets dans lequel ces lignes commencent et se terminent. Créons un tel tableau et décrivons-le uniquement avec des index de vertex, 2 index par ligne (le début de la ligne et la fin). Et un peu plus loin, lorsque nous dessinons ces lignes, nous pouvons facilement obtenir leurs coordonnées à partir du tableau de sommets. Mon tableau de lignes (je l'ai appelé bords, car ce sont les bords du cube) J'ai créé un tableau de sommets ci-dessous et il ressemble à ceci:2 index sur chaque ligne (le début de la ligne et la fin). Et un peu plus loin, lorsque nous dessinons ces lignes, nous pouvons facilement obtenir leurs coordonnées à partir du tableau de sommets. Mon tableau de lignes (je l'ai appelé bords, car ce sont les bords du cube) J'ai créé un tableau de sommets ci-dessous et il ressemble à ceci:2 index sur chaque ligne (le début de la ligne et la fin). Et un peu plus loin, lorsque nous dessinons ces lignes, nous pouvons facilement obtenir leurs coordonnées à partir du tableau de sommets. Mon tableau de lignes (je l'ai appelé bords, car ce sont les bords du cube) J'ai créé un tableau de sommets ci-dessous et il ressemble à ceci:
const edges = [
[0, 1],
[1, 2],
[2, 3],
[3, 0],
[0, 4],
[1, 5],
[2, 6],
[3, 7],
[4, 5],
[5, 6],
[6, 7],
[7, 4],
];
Il y a 12 paires d'indices dans ce tableau, 2 indices de sommet par ligne.Faisons connaissance avec une autre matrice qui augmentera notre cube, et enfin essayons de le dessiner à l'écran. La matrice d'échelle ressemble à ceci:
Les paramètres sx, sy, sz sur la diagonale principale signifient combien de fois nous voulons augmenter l'objet. Si nous substituons 10, 10, 10 dans la matrice au lieu de sx, sy, sz et multiplions cette matrice par les sommets du cube, cela rendra notre cube dix fois plus grand et il ne sera plus 2 par 2 par 2, mais 20 par 20 par 20.Pour la matrice de mise à l'échelle, ainsi que pour la matrice de déplacement, nous implémentons la méthode dans la classe Matrix, qui renverra la matrice avec les arguments déjà substitués:static getScale(sx, sy, sz) {
return [
[sx, 0, 0, 0],
[0, sy, 0, 0],
[0, 0, sz, 0],
[0, 0, 0, 1],
]
}
Convoyeur de visualisation
Si nous essayons maintenant de dessiner un cube avec des lignes en utilisant les coordonnées actuelles des sommets, nous obtiendrons un très petit cube de deux pixels dans le coin supérieur gauche de l'écran, car l'origine de la toile est là. Passons en revue tous les sommets du cube et multiplions-les par la matrice de mise à l'échelle pour agrandir le cube, puis par la matrice de déplacement pour voir le cube non pas dans le coin supérieur gauche, mais au milieu de l'écran, j'ai le code pour énumérer les sommets avec la multiplication de matrice ci-dessous tableau d'arêtes, et ressemble à ceci:const sceneVertices = []
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
Matrix.getScale(100, 100, 100),
vertices[i]
);
vertex = Matrix.multiplyVector(
Matrix.getTranslation(400, -300, 0),
vertex
);
sceneVertices.push(vertex);
}
Veuillez noter que nous ne modifions pas les sommets d'origine du cube, mais sauvegardons le résultat de la multiplication dans le tableau sceneVertices, car nous pouvons vouloir dessiner plusieurs cubes de tailles différentes dans des coordonnées différentes, et si nous modifions les coordonnées initiales, nous ne pourrons pas dessiner le cube suivant, t .à. il n'y a rien pour commencer, les coordonnées initiales seront corrompues par le premier cube. Dans le code ci-dessus, j'ai augmenté le cube d'origine de 100 fois dans toutes les directions, grâce à la multiplication de tous les sommets par la matrice de mise à l'échelle avec les arguments 100, 100, 100, et j'ai également déplacé tous les sommets du cube vers la droite et abaissé respectivement de 400 et -300 pixels, car nous avons les tailles de toile de l'article précédent sont de 800 par 600, ce sera juste la moitié de la largeur et de la hauteur de la zone de dessin, en d'autres termes, le centre.Nous avons terminé avec les sommets jusqu'à présent, mais nous devons encore dessiner tout cela en utilisant drawLine et le tableau des bords, écrivons une autre boucle sous la boucle des sommets pour itérer sur les bords et dessiner toutes les lignes dedans:drawer.clearSurface()
for (let i = 0, l = edges.length ; i < l ; i++) {
const e = edges[i]
drawer.drawLine(
sceneVertices[e[0]].x,
sceneVertices[e[0]].y,
sceneVertices[e[1]].x,
sceneVertices[e[1]].y,
0, 0, 255
)
}
ctx.putImageData(imageData, 0, 0)
Rappelons que dans le dernier article, nous commençons tout le dessin en effaçant l'écran de l'état précédent en appelant la méthode clearSurface, puis j'itère sur toutes les faces du cube et dessine le cube avec des lignes bleues (0, 0, 255), et je prends les coordonnées des lignes du tableau sceneVertices, t .à. il y a déjà des sommets redimensionnés et déplacés dans le cycle précédent, mais les indices de ces sommets coïncident avec les indices des sommets d'origine du tableau de sommets, car Je les ai traités et les ai placés dans le tableau sceneVertices sans changer l'ordre. Si nous exécutons le code maintenant, nous ne verrons rien à l'écran. En effet, dans notre système de coordonnées, Y regarde vers le haut et dans le système de coordonnées, canvas regarde vers le bas. Il s'avère qu'il y a notre cube, mais il est en dehors de l'écran et pour résoudre ce problème, nous devons retourner l'image en Y (miroir) avant de dessiner un pixel dans la classe Drawer. Jusqu'à présent, cette option nous suffira, par conséquent, le code pour dessiner un pixel pour moi ressemble à ceci:drawPixel(x, y, r, g, b) {
const offset = (this.width * -y + x) * 4;
if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
this.surface[offset] = r;
this.surface[offset + 1] = g;
this.surface[offset + 2] = b;
this.surface[offset + 3] = 255;
}
}
On peut voir que dans la formule pour obtenir le décalage, Y est maintenant avec un signe moins et l'axe regarde maintenant dans la direction dont nous avons besoin, également dans cette méthode, j'ai ajouté une vérification pour aller au-delà des limites du tableau de pixels. Certaines autres optimisations sont apparues dans la classe Drawer en raison des commentaires sur l'article précédent, donc je poste toute la classe Drawer avec quelques optimisations et vous pouvez remplacer l'ancien tiroir par celui-ci:Code de classe de tiroir amélioréclass Drawer {
surface = null;
width = 0;
height = 0;
constructor(surface, width, height) {
this.surface = surface;
this.width = width;
this.height = height;
}
drawPixel(x, y, r, g, b) {
const offset = (this.width * -y + x) * 4;
if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
this.surface[offset] = r;
this.surface[offset + 1] = g;
this.surface[offset + 2] = b;
this.surface[offset + 3] = 255;
}
}
drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
const round = Math.trunc;
x1 = round(x1);
y1 = round(y1);
x2 = round(x2);
y2 = round(y2);
const c1 = y2 - y1;
const c2 = x2 - x1;
const length = Math.max(
Math.abs(c1),
Math.abs(c2)
);
const xStep = c2 / length;
const yStep = c1 / length;
for (let i = 0 ; i <= length ; i++) {
this.drawPixel(
Math.trunc(x1 + xStep * i),
Math.trunc(y1 + yStep * i),
r, g, b,
);
}
}
clearSurface() {
const surfaceSize = this.width * this.height * 4;
for (let i = 0; i < surfaceSize; i++) {
this.surface[i] = 0;
}
}
}
const drawer = new Drawer(
imageData.data,
imageData.width,
imageData.height
);
Si vous exécutez le code maintenant, l'image suivante apparaîtra à l'écran:
Pi / 2(Il existe également une valeur Pi approximative dans JS, c'est la constante Math.PI). Ajoutons 3 méthodes à la classe Matrix pour obtenir des matrices de rotation, avec un angle de rotation accepté en degrés, que nous convertirons en radians, car ils sont nécessaires au fonctionnement des fonctions sin / cos:static getRotationX(angle) {
const rad = Math.PI / 180 * angle;
return [
[1, 0, 0, 0],
[0, Math.cos(rad), -Math.sin(rad), 0],
[0, Math.sin(rad), Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationY(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), 0, Math.sin(rad), 0],
[0, 1, 0, 0],
[-Math.sin(rad), 0, Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationZ(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), -Math.sin(rad), 0, 0],
[Math.sin(rad), Math.cos(rad), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
];
}
Les 3 méthodes commencent par convertir les degrés en radians, après quoi nous substituons l'angle de rotation en radians dans la matrice de rotation, en passant les angles dans les fonctions sin et cos. Pourquoi la matrice est-elle telle, vous pouvez en savoir plus sur le hub dans les articles thématiques, avec une explication très détaillée, sinon vous pouvez percevoir ces matrices comme des formules qui ont été calculées pour nous et nous pouvons être sûrs qu'elles fonctionnent.Ci-dessus dans le code, nous avons implémenté 2 cycles, le premier convertit les sommets, le second dessine des lignes par les indices des sommets, par conséquent, nous obtenons une image à l'écran à partir des sommets, et appelons cette section de code le pipeline de visualisation. Le convoyeur parce que nous prenons le pic et faisons à son tour différentes opérations avec lui, échelle, décalage, rotation, rendu, comme sur un convoyeur industriel normal. Ajoutons maintenant au premier cycle du pipeline de visualisation, en plus de la mise à l'échelle, la rotation autour des axes. Tout d'abord, je vais tourner autour de X, puis autour de Y, puis augmenter le modèle et le déplacer (les 2 dernières actions sont déjà là), donc tout le code de la boucle sera comme ceci:for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
Matrix.getRotationX(20),
vertices[i]
);
vertex = Matrix.multiplyVector(
Matrix.getRotationY(20),
vertex
);
vertex = Matrix.multiplyVector(
Matrix.getScale(100, 100, 100),
vertex
);
vertex = Matrix.multiplyVector(
Matrix.getTranslation(400, -300, 0),
vertex
);
sceneVertices.push(vertex);
}
Dans cet exemple, j'ai fait pivoter tous les sommets autour de l'axe X de 20 degrés, puis autour de Y de 20 degrés et j'avais déjà 2 transformations restantes. Si vous avez tout fait correctement, votre cube devrait maintenant avoir l'air en trois dimensions:Tourner autour des axes a une caractéristique, par exemple, si vous tournez d'abord le cube autour de l'axe Y, puis autour de l'axe X, les résultats seront différents:Il existe d'autres fonctionnalités, par exemple, si vous tournez le cube de 90 degrés sur l'axe X, puis de 90 degrés sur l'axe Y et enfin de 90 degrés autour de l'axe Z, la dernière rotation autour de Z annulera la rotation autour de X et vous obtiendrez la même chose le résultat est comme si vous veniez de faire pivoter la figure de 90 degrés autour de l'axe Y. Pour voir pourquoi cela se produit, prenez un objet rectangulaire (ou cubique) dans vos mains (par exemple le cube Rubik assemblé), souvenez-vous de la position initiale de l'objet et faites-le pivoter de 90 degrés en premier autour de X imaginaire, puis à 90 degrés autour de Y et à 90 degrés autour de Z et rappelez-vous de quel côté il est devenu vers vous, puis partez de la position initiale dont vous vous êtes souvenu plus tôt et faites de même, en supprimant les tours de X et Z, tournez uniquement autour Y - vous verrez que le résultat est le même.Maintenant, nous ne résoudrons pas ce problème et n'entrerons pas dans ses détails, une telle rotation pour le moment nous convient tout à fait, mais nous mentionnerons ce problème dans la troisième partie (si vous voulez en savoir plus maintenant, essayez de rechercher des articles sur le hub par la requête "verrou à charnière") .Maintenant, optimisons un peu notre code, il a été mentionné ci-dessus que les transformations matricielles peuvent être combinées entre elles en multipliant les matrices de transformation. Essayons de ne pas multiplier chaque vecteur d'abord par la matrice de rotation autour de X, puis autour de Y, puis à l'échelle et à la fin du mouvement, et d'abord, avant la boucle, nous multiplions toutes les matrices, et dans la boucle nous multiplierons chaque sommet par une seule matrice résultante, j'ai le code est sorti comme ceci:let matrix = Matrix.getRotationX(20);
matrix = Matrix.multiply(
Matrix.getRotationY(20),
matrix
);
matrix = Matrix.multiply(
Matrix.getScale(100, 100, 100),
matrix,
);
matrix = Matrix.multiply(
Matrix.getTranslation(400, -300, 0),
matrix,
);
const sceneVertices = [];
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
matrix,
vertices[i]
);
sceneVertices.push(vertex);
}
Dans cet exemple, la combinaison des transformations est effectuée 1 fois avant le cycle, et donc nous n'avons qu'une seule multiplication matricielle avec chaque sommet. Si vous exécutez ce code, le modèle de cube doit rester le même.Ajoutons l'animation la plus simple, à savoir, nous allons changer l'angle de rotation autour de l'axe Y dans l'intervalle, par exemple, nous allons changer l'angle de rotation autour de l'axe Y de 1 degré, toutes les 100 millisecondes. Pour ce faire, mettez le code du pipeline de visualisation dans la fonction setInterval, que nous avons d'abord utilisée dans le 1er article. Le code du pipeline d'animation ressemble à ceci:let angle = 0
setInterval(() => {
let matrix = Matrix.getRotationX(20)
matrix = Matrix.multiply(
Matrix.getRotationY(angle += 1),
matrix
)
matrix = Matrix.multiply(
Matrix.getScale(100, 100, 100),
matrix,
)
matrix = Matrix.multiply(
Matrix.getTranslation(400, -300, 0),
matrix,
)
const sceneVertices = []
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
matrix,
vertices[i]
)
sceneVertices.push(vertex)
}
drawer.clearSurface()
for (let i = 0, l = edges.length ; i < l ; i++) {
const e = edges[i]
drawer.drawLine(
sceneVertices[e[0]].x,
sceneVertices[e[0]].y,
sceneVertices[e[1]].x,
sceneVertices[e[1]].y,
0, 0, 255
)
}
ctx.putImageData(imageData, 0, 0)
}, 100)
Le résultat devrait être comme ceci:La dernière chose que nous allons faire dans cette partie est d'afficher les axes du système de coordonnées à l'écran de manière à ce qu'il soit visible autour duquel tourne notre cube. Nous dessinons l'axe Y du centre vers le haut, 200 pixels de long, l'axe X, à droite, également 200 pixels de long, et l'axe Z, dessinons 150 pixels vers le bas et à gauche (en diagonale), comme indiqué au tout début de l'article sur la figure du système de coordonnées droitier . Commençons par la partie la plus simple, ce sont les axes X, Y, car leur ligne se déplace dans une seule direction. Après la boucle qui dessine le cube (boucle des bords), ajoutez le rendu des axes X, Y:const center = new Vector(400, -300, 0)
drawer.drawLine(
center.x, center.y,
center.x, center.y + 200,
150, 150, 150
)
drawer.drawLine(
center.x, center.y,
center.x + 200, center.y,
150, 150, 150
)
Le vecteur central est le milieu de la fenêtre de dessin, car nous avons les dimensions actuelles de 800 par 600 et -300 pour Y, je l'ai indiqué, car la fonction drawPixel retourne Y et rend sa direction adaptée au canevas (dans canevas, Y regarde vers le bas). Ensuite, nous dessinons 2 axes à l'aide de drawLine, en décalant d'abord Y 200 pixels vers le haut (fin de la ligne de l'axe Y), puis X 200 pixels vers la droite (fin de la ligne de l'axe X). Résultat: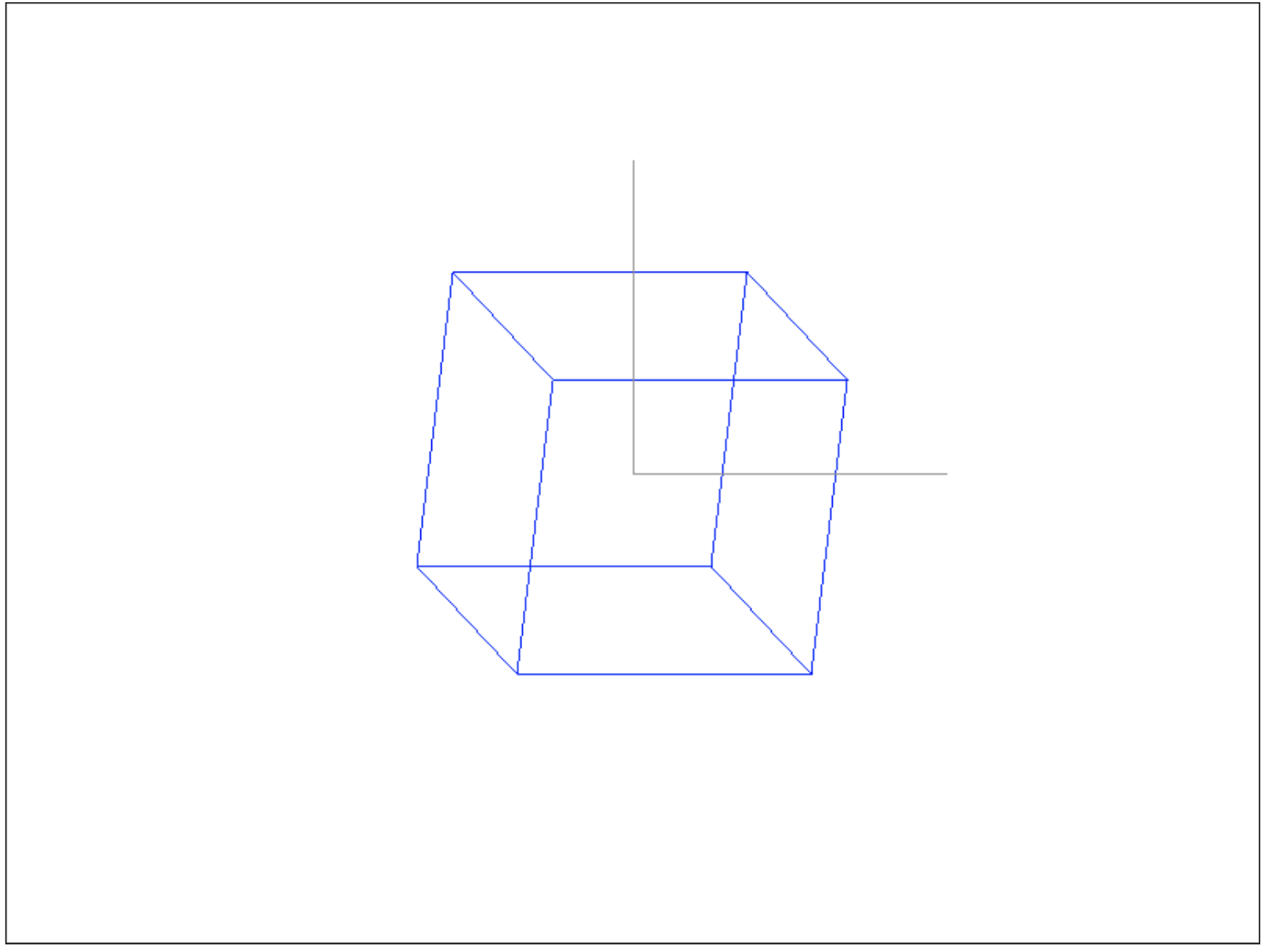
const zVector = new Vector(-1, -1, 0);
const zCoords = Vector.add(
center,
zVector.normalize().multiplyByScalar(150)
);
drawer.drawLine(
center.x, center.y,
zCoords.x, zCoords.y,
150, 150, 150
);
Et en conséquence, vous obtenez les 3 axes de la longueur souhaitée:Dans cet exemple, l'axe Z ne montre que le système de coordonnées que nous avons, nous l'avons dessiné en diagonale pour qu'il soit visible, car le véritable axe Z est perpendiculaire à notre regard, et nous pourrions le dessiner avec un point sur l'écran, ce qui ne serait pas beau.Au total, dans cet article, nous avons essentiellement compris les systèmes de coordonnées, les vecteurs et avec certaines opérations sur eux, les matrices et leurs rôles dans les transformations de coordonnées, trié les sommets et écrit un simple convoyeur pour visualiser le cube et les axes du système de coordonnées, fixant la théorie avec la pratique. Tout le code d'application est disponible sous le spoiler:Code pour toute l'applicationconst ctx = document.getElementById('surface').getContext('2d');
const imageData = ctx.createImageData(800, 600);
class Vector {
x = 0;
y = 0;
z = 0;
w = 1;
constructor(x, y, z, w = 1) {
this.x = x;
this.y = y;
this.z = z;
this.w = w;
}
multiplyByScalar(s) {
this.x *= s;
this.y *= s;
this.z *= s;
return this;
}
static add(v1, v2) {
return new Vector(
v1.x + v2.x,
v1.y + v2.y,
v1.z + v2.z,
);
}
getLength() {
return Math.sqrt(
this.x * this.x + this.y * this.y + this.z * this.z
);
}
normalize() {
const length = this.getLength();
this.x /= length;
this.y /= length;
this.z /= length;
return this;
}
}
class Matrix {
static multiply(a, b) {
const m = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
];
for (let i = 0 ; i < 4 ; i++) {
for(let j = 0 ; j < 4 ; j++) {
m[i][j] = a[i][0] * b[0][j] +
a[i][1] * b[1][j] +
a[i][2] * b[2][j] +
a[i][3] * b[3][j];
}
}
return m;
}
static getRotationX(angle) {
const rad = Math.PI / 180 * angle;
return [
[1, 0, 0, 0],
[0, Math.cos(rad), -Math.sin(rad), 0],
[0, Math.sin(rad), Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationY(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), 0, Math.sin(rad), 0],
[0, 1, 0, 0],
[-Math.sin(rad), 0, Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationZ(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), -Math.sin(rad), 0, 0],
[Math.sin(rad), Math.cos(rad), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
];
}
static getTranslation(dx, dy, dz) {
return [
[1, 0, 0, dx],
[0, 1, 0, dy],
[0, 0, 1, dz],
[0, 0, 0, 1],
];
}
static getScale(sx, sy, sz) {
return [
[sx, 0, 0, 0],
[0, sy, 0, 0],
[0, 0, sz, 0],
[0, 0, 0, 1],
];
}
static multiplyVector(m, v) {
return new Vector(
m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
);
}
}
class Drawer {
surface = null;
width = 0;
height = 0;
constructor(surface, width, height) {
this.surface = surface;
this.width = width;
this.height = height;
}
drawPixel(x, y, r, g, b) {
const offset = (this.width * -y + x) * 4;
if (x >= 0 && x < this.width && -y >= 0 && -y < this.height) {
this.surface[offset] = r;
this.surface[offset + 1] = g;
this.surface[offset + 2] = b;
this.surface[offset + 3] = 255;
}
}
drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
const round = Math.trunc;
x1 = round(x1);
y1 = round(y1);
x2 = round(x2);
y2 = round(y2);
const c1 = y2 - y1;
const c2 = x2 - x1;
const length = Math.max(
Math.abs(c1),
Math.abs(c2)
);
const xStep = c2 / length;
const yStep = c1 / length;
for (let i = 0 ; i <= length ; i++) {
this.drawPixel(
Math.trunc(x1 + xStep * i),
Math.trunc(y1 + yStep * i),
r, g, b,
);
}
}
clearSurface() {
const surfaceSize = this.width * this.height * 4;
for (let i = 0; i < surfaceSize; i++) {
this.surface[i] = 0;
}
}
}
const drawer = new Drawer(
imageData.data,
imageData.width,
imageData.height
);
const vertices = [
new Vector(-1, 1, 1),
new Vector(-1, 1, -1),
new Vector(1, 1, -1),
new Vector(1, 1, 1),
new Vector(-1, -1, 1),
new Vector(-1, -1, -1),
new Vector(1, -1, -1),
new Vector(1, -1, 1),
];
const edges = [
[0, 1],
[1, 2],
[2, 3],
[3, 0],
[0, 4],
[1, 5],
[2, 6],
[3, 7],
[4, 5],
[5, 6],
[6, 7],
[7, 4],
];
let angle = 0;
setInterval(() => {
let matrix = Matrix.getRotationX(20);
matrix = Matrix.multiply(
Matrix.getRotationY(angle += 1),
matrix
);
matrix = Matrix.multiply(
Matrix.getScale(100, 100, 100),
matrix,
);
matrix = Matrix.multiply(
Matrix.getTranslation(400, -300, 0),
matrix,
);
const sceneVertices = [];
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
matrix,
vertices[i]
);
sceneVertices.push(vertex);
}
drawer.clearSurface();
for (let i = 0, l = edges.length ; i < l ; i++) {
const e = edges[i];
drawer.drawLine(
sceneVertices[e[0]].x,
sceneVertices[e[0]].y,
sceneVertices[e[1]].x,
sceneVertices[e[1]].y,
0, 0, 255
);
}
const center = new Vector(400, -300, 0)
drawer.drawLine(
center.x, center.y,
center.x, center.y + 200,
150, 150, 150
);
drawer.drawLine(
center.x, center.y,
center.x + 200, center.y,
150, 150, 150
);
const zVector = new Vector(-1, -1, 0, 0);
const zCoords = Vector.add(
center,
zVector.normalize().multiplyByScalar(150)
);
drawer.drawLine(
center.x, center.y,
zCoords.x, zCoords.y,
150, 150, 150
);
ctx.putImageData(imageData, 0, 0);
}, 100);
Et après?
Dans la partie suivante, nous verrons comment contrôler la caméra et comment faire une projection (plus l'objet est éloigné, plus il est petit), apprendre à connaître les triangles et découvrir comment les modèles 3D peuvent être construits à partir d'eux, analyser ce que sont les normales et pourquoi elles sont nécessaires.