En prévision du début du cours, "Algorithmes pour les développeurs" a préparé pour vous une traduction d'un autre matériel utile.
Le codage Huffman est un algorithme de compression de données qui formule l'idée de base de la compression de fichiers. Dans cet article, nous parlerons du codage de longueur fixe et variable, des codes décodés de manière unique, des règles de préfixe et de la construction d'un arbre Huffman.Nous savons que chaque caractère est stocké sous la forme d'une séquence de 0 et 1 et prend 8 bits. C'est ce qu'on appelle le codage à longueur fixe car chaque caractère utilise le même nombre fixe de bits à stocker.Disons que le texte est donné. Comment pouvons-nous réduire la quantité d'espace nécessaire pour stocker un personnage?L'idée de base est le codage à longueur variable. Nous pouvons utiliser le fait que certains caractères du texte sont plus courants que d'autres ( voir ici ) pour développer un algorithme qui représentera la même séquence de caractères avec moins de bits. Lors du codage d'une longueur variable, nous attribuons un nombre variable de bits aux caractères en fonction de la fréquence de leur apparition dans ce texte. En fin de compte, certains caractères peuvent prendre seulement 1 bit, et d'autres 2 bits, 3 ou plus. Le problème avec le codage de longueur variable n'est que le décodage ultérieur de la séquence.Comment, en connaissant la séquence de bits, la décoder de façon unique?Considérez la chaîne «aabacdab» . Il a 8 caractères et lors du codage d'une longueur fixe, 64 bits seront nécessaires pour le stocker. Notez que la fréquence des caractères «a», «b», «c» et «d» est respectivement de 4, 2, 1, 1. Essayons d'imaginer «aabacdab» avec moins de bits, en utilisant le fait que «a» est plus commun que «b» et «b» est plus commun que «c» et «d» . Pour commencer, nous codons «a» en utilisant un bit égal à 0, «b» nous attribuons un code à deux bits 11, et en utilisant trois bits 100 et 011, nous codons «c» et"D" .En conséquence, nous réussirons:Ainsi, nous codons la chaîne «aabacdab» comme 00110100011011 (0 | 0 | 11 | 0 | 100 | 011 | 0 | 11) en utilisant les codes présentés ci-dessus. Cependant, le principal problème sera le décodage. Lorsque nous essayons de décoder la ligne 00110100011011 , nous obtenons un résultat ambigu, car il peut être représenté comme:0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
...etc.Pour éviter cette ambiguïté, nous devons nous assurer que notre codage satisfait le concept d'une règle de préfixe , ce qui implique à son tour que les codes peuvent être décodés d'une seule manière unique. Une règle de préfixe garantit qu'aucun code n'est le préfixe d'un autre. Par code, nous entendons des bits utilisés pour représenter un caractère particulier. Dans l'exemple ci-dessus, 0 est le préfixe 011 , ce qui viole la règle de préfixe. Donc, si nos codes satisfont à la règle du préfixe, alors nous pouvons décoder de manière unique (et vice versa).Passons en revue l'exemple ci-dessus. Cette fois, nous allons attribuer les caractères "a", "b", "c" et "d" Codes qui satisfont à la règle de préfixe.En utilisant cet encodage, la chaîne «aabacdab» sera encodée en 00100100011010 (0 | 0 | 10 | 0 | 100 | 011 | 0 | 10) . Et ici 00100100011010, nous pouvons décoder de manière unique et revenir à notre ligne d'origine "aabacdab" .Codage Huffman
Maintenant que nous avons compris le codage de longueur variable et une règle de préfixe, parlons du codage Huffman.La méthode est basée sur la création d'arbres binaires. Dans celui-ci, un nœud peut être fini ou interne. Initialement, tous les nœuds sont considérés comme des feuilles (feuilles), qui représentent le symbole lui-même et son poids (c'est-à-dire la fréquence d'occurrence). Les nœuds internes contiennent le poids du caractère et se réfèrent à deux nœuds descendants. D'un commun accord, le bit «0» représente un suivi sur la branche gauche et «1» représente sur la droite. Dans un arbre complet, il y a N feuilles et N-1 nœuds internes. Il est recommandé que lors de la construction d'un arbre Huffman, les caractères inutilisés soient supprimés pour obtenir des codes de longueur optimale.Nous utiliserons la file d'attente prioritaire pour construire l'arbre Huffman, où le nœud avec la fréquence la plus basse recevra la priorité la plus élevée. Les étapes de construction sont décrites ci-dessous:- Créez un nœud feuille pour chaque personnage et ajoutez-les à la file d'attente prioritaire.
- Pendant que vous êtes en ligne pour plusieurs feuilles, procédez comme suit:
- Supprimez les deux nœuds avec la priorité la plus élevée (avec la fréquence la plus basse) de la file d'attente;
- Créez un nouveau nœud interne où ces deux nœuds seront héritiers et la fréquence d'occurrence sera égale à la somme des fréquences de ces deux nœuds.
- Ajoutez un nouveau nœud à la file d'attente prioritaire.
- Le seul nœud restant sera la racine, ceci terminera la construction de l'arbre.
Imaginez que nous ayons du texte composé uniquement des caractères «a», «b», «c», «d» et «e», et les fréquences de leur apparition sont respectivement 15, 7, 6, 6 et 5. Voici des illustrations qui reflètent les étapes de l'algorithme.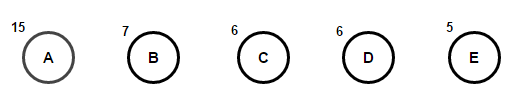
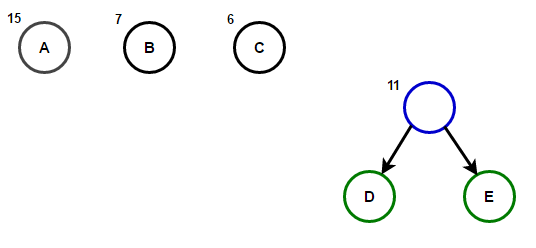
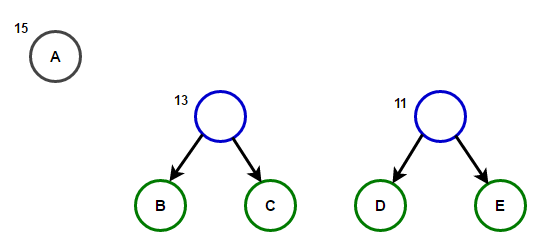
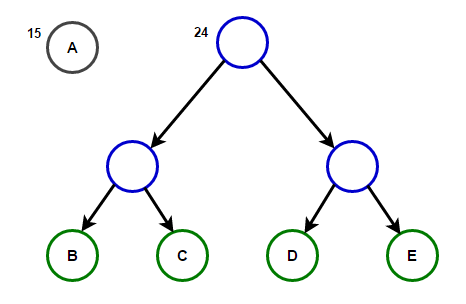
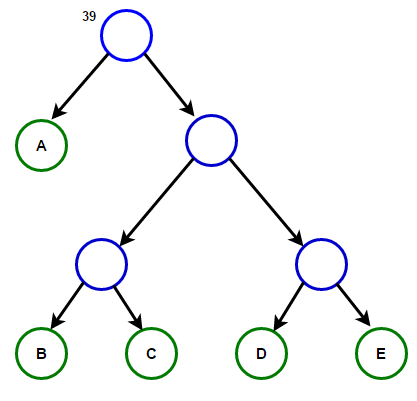 Le chemin de la racine à n'importe quel nœud d'extrémité stockera le code de préfixe optimal (également connu sous le nom de code Huffman) correspondant au caractère associé à ce nœud d'extrémité.
Le chemin de la racine à n'importe quel nœud d'extrémité stockera le code de préfixe optimal (également connu sous le nom de code Huffman) correspondant au caractère associé à ce nœud d'extrémité.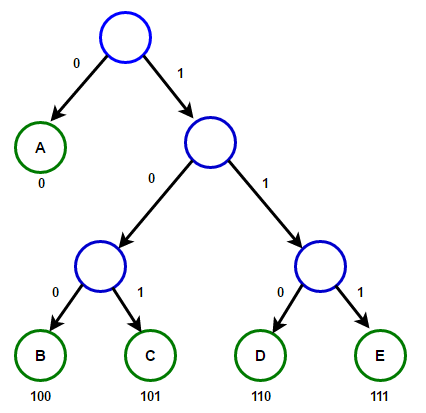 Huffman TreeCi-dessous vous trouverez l'implémentation de l'algorithme de compression Huffman en C ++ et Java:
Huffman TreeCi-dessous vous trouverez l'implémentation de l'algorithme de compression Huffman en C ++ et Java:#include <iostream>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
struct Node
{
char ch;
int freq;
Node *left, *right;
};
Node* getNode(char ch, int freq, Node* left, Node* right)
{
Node* node = new Node();
node->ch = ch;
node->freq = freq;
node->left = left;
node->right = right;
return node;
}
struct comp
{
bool operator()(Node* l, Node* r)
{
return l->freq > r->freq;
}
};
void encode(Node* root, string str,
unordered_map<char, string> &huffmanCode)
{
if (root == nullptr)
return;
if (!root->left && !root->right) {
huffmanCode[root->ch] = str;
}
encode(root->left, str + "0", huffmanCode);
encode(root->right, str + "1", huffmanCode);
}
void decode(Node* root, int &index, string str)
{
if (root == nullptr) {
return;
}
if (!root->left && !root->right)
{
cout << root->ch;
return;
}
index++;
if (str[index] =='0')
decode(root->left, index, str);
else
decode(root->right, index, str);
}
void buildHuffmanTree(string text)
{
unordered_map<char, int> freq;
for (char ch: text) {
freq[ch]++;
}
priority_queue<Node*, vector<Node*>, comp> pq;
for (auto pair: freq) {
pq.push(getNode(pair.first, pair.second, nullptr, nullptr));
}
while (pq.size() != 1)
{
Node *left = pq.top(); pq.pop();
Node *right = pq.top(); pq.pop();
int sum = left->freq + right->freq;
pq.push(getNode('\0', sum, left, right));
}
Node* root = pq.top();
unordered_map<char, string> huffmanCode;
encode(root, "", huffmanCode);
cout << "Huffman Codes are :\n" << '\n';
for (auto pair: huffmanCode) {
cout << pair.first << " " << pair.second << '\n';
}
cout << "\nOriginal string was :\n" << text << '\n';
string str = "";
for (char ch: text) {
str += huffmanCode[ch];
}
cout << "\nEncoded string is :\n" << str << '\n';
int index = -1;
cout << "\nDecoded string is: \n";
while (index < (int)str.size() - 2) {
decode(root, index, str);
}
}
int main()
{
string text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
return 0;
}
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class Node
{
char ch;
int freq;
Node left = null, right = null;
Node(char ch, int freq)
{
this.ch = ch;
this.freq = freq;
}
public Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
};
class Huffman
{
public static void encode(Node root, String str,
Map<Character, String> huffmanCode)
{
if (root == null)
return;
if (root.left == null && root.right == null) {
huffmanCode.put(root.ch, str);
}
encode(root.left, str + "0", huffmanCode);
encode(root.right, str + "1", huffmanCode);
}
public static int decode(Node root, int index, StringBuilder sb)
{
if (root == null)
return index;
if (root.left == null && root.right == null)
{
System.out.print(root.ch);
return index;
}
index++;
if (sb.charAt(index) == '0')
index = decode(root.left, index, sb);
else
index = decode(root.right, index, sb);
return index;
}
public static void buildHuffmanTree(String text)
{
Map<Character, Integer> freq = new HashMap<>();
for (int i = 0 ; i < text.length(); i++) {
if (!freq.containsKey(text.charAt(i))) {
freq.put(text.charAt(i), 0);
}
freq.put(text.charAt(i), freq.get(text.charAt(i)) + 1);
}
PriorityQueue<Node> pq = new PriorityQueue<>(
(l, r) -> l.freq - r.freq);
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
pq.add(new Node(entry.getKey(), entry.getValue()));
}
while (pq.size() != 1)
{
Node left = pq.poll();
Node right = pq.poll();
int sum = left.freq + right.freq;
pq.add(new Node('\0', sum, left, right));
}
Node root = pq.peek();
Map<Character, String> huffmanCode = new HashMap<>();
encode(root, "", huffmanCode);
System.out.println("Huffman Codes are :\n");
for (Map.Entry<Character, String> entry : huffmanCode.entrySet()) {
System.out.println(entry.getKey() + " " + entry.getValue());
}
System.out.println("\nOriginal string was :\n" + text);
StringBuilder sb = new StringBuilder();
for (int i = 0 ; i < text.length(); i++) {
sb.append(huffmanCode.get(text.charAt(i)));
}
System.out.println("\nEncoded string is :\n" + sb);
int index = -1;
System.out.println("\nDecoded string is: \n");
while (index < sb.length() - 2) {
index = decode(root, index, sb);
}
}
public static void main(String[] args)
{
String text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
}
}
Remarque: la mémoire utilisée par la chaîne d'entrée est de 47 * 8 = 376 bits, et la chaîne codée ne prend que 194 bits, c'est-à-dire les données sont compressées d'environ 48%. Dans le programme C ++ ci-dessus, nous utilisons la classe de chaîne pour stocker la chaîne codée pour rendre le programme lisible.Étant donné que les structures de données efficaces de la file d'attente prioritaire nécessitent un temps O (log (N)) pour être insérées, et dans un arbre binaire complet avec N feuilles, il y a 2N-1 nœuds, et l'arbre Huffman est un arbre binaire complet, l'algorithme fonctionne pour O (Nlog (N )) heure, où N est le nombre de caractères.Sources:
en.wikipedia.org/wiki/Huffman_codingen.wikipedia.org/wiki/Variable-length_codewww.youtube.com/watch?v=5wRPin4oxCo
.