Est-ce que cela vous semble familier: "J'ai commencé à faire du développement web après avoir suivi des cours"?Vous souhaitez peut-être améliorer vos connaissances sur les bases de l'informatique en termes de structures de données et d'algorithmes. Aujourd'hui, nous allons parler de certaines des structures de données les plus courantes à l'aide de l'exemple JS.1. Pile (appels) (Pile)
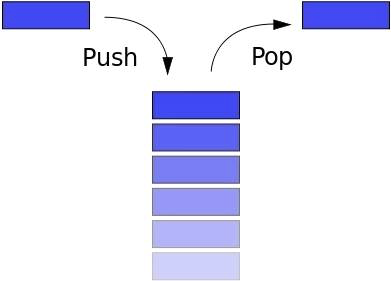La pile suit le principe LIFO (Last In First Out - Last In, First Out). Si vous empilez les livres les uns sur les autres et que vous souhaitez prendre le livre le plus bas, prenez d'abord le livre du haut, puis le suivant, etc. Le bouton "Retour" du navigateur vous permet de revenir (revenir) à la page précédente.La pile a les méthodes suivantes:- pousser: ajouter un nouvel élément
- pop: supprimer l'élément supérieur, le renvoyer
- coup d'œil: retourner l'élément supérieur
- longueur: retourne le nombre d'éléments sur la pile
Un tableau dans JS a des attributs de pile, mais nous allons le construire à partir de zéro en utilisant la fonction Stack ():function Stack() {
this.count = 0
this.storage = {}
this.push = function(value) {
this.storage[this.count] = value
this.count++
}
this.pop = function() {
if (this.count === 0) return undefined
this.count--
let result = this.storage[this.count]
delete this.storage[this.count]
return result
}
this.peek = function() {
return this.storage[this.count - 1]
}
this.size = function() {
return this.count
}
}
2. File d'attente (File d'attente)
Une file d'attente ressemble à une pile. La différence est que la file d'attente suit le principe FIFO (First In First Out - premier entré, premier sorti). Lorsque vous faites la queue, le premier sera toujours le premier.La file d'attente a les méthodes suivantes:- mettre en file d'attente: entrer dans la file d'attente, ajouter un élément à la fin
- dequeue: quitter la file d'attente, supprimer le premier élément et le renvoyer
- avant: obtenir le premier élément
- isEmpty: vérifie si la file d'attente est vide
- taille: obtenir le nombre d'éléments dans la file d'attente
Un tableau dans JS a certains attributs de file d'attente, nous pouvons donc l'utiliser pour la démonstration:function Queue() {
let collection = []
this.print = function() {
console.log(collection)
}
this.enqueue = function(element) {
collection.push(element)
}
this.dequeue = function() {
return collection.shift()
}
this.front = function() {
return collection[0]
}
this.isEmpty = function() {
return collection.length === 0
}
this.size = function() {
return collection.length
}
}
L'ordre de priorité (priorité)
La file d'attente a une version avancée. Attribuez une priorité à chaque élément et les éléments seront triés en conséquence:function PriorityQueue() {
...
this.enqueue = function(element) {
if (this.isEmpty()) {
collection.push(element)
} else {
let added = false
for (let i = 0; i < collection.length; i++) {
if (element[1] < collection[i][1]) {
collection.splice(i, 0, element)
added = true
break;
}
}
if (!added) {
collection.push(element)
}
}
}
}
Essai:let pQ = new PriorityQueue()
pQ.enqueue([gannicus, 3])
pQ.enqueue([spartacus, 1])
pQ.enqueue([crixus, 2])
pQ.enqueue([oenomaus, 4])
pQ.print()
RĂ©sultat:[
[spartacus, 1],
[crixus, 2],
[gannicus, 3],
[oenomaus, 4]
]
3. Une liste chaînée (liste chaînée de nœuds et de liens ou pointeurs) (liste chaînée)
Littéralement, une liste chaînée est une structure de données chaînée, où chaque nœud se compose de deux parties: les données du nœud et un pointeur vers le nœud suivant. La liste chaînée et le tableau conditionnel sont des structures de données linéaires avec stockage sérialisé. Les différences sont les suivantes:Une liste liée individuellement a les méthodes suivantes:- taille: retourne le nombre de nœuds
- tête: retourne le premier élément (tête - tête)
- add: ajoute un élément à la fin (queue - queue)
- supprimer: supprimer plusieurs nœuds
- indexOf: retourne l'index du nœud
- elementAt: retourne le noeud par index
- addAt: insère un nœud à un endroit spécifique (par index)
- removeAt: supprime un nœud spécifique (par index)
function Node(element) {
this.element = element
this.next = null
}
function LinkedList() {
let length = 0
let head = null
this.size = function() {
return length
}
this.head = function() {
return head
}
this.add = function(element) {
let node = new Node(element)
if (head === null) {
head = node
} else {
let currentNode = head
while (currentNode.next) {
currentNode = currentNode.next
}
currentNode.next = node
}
length++
}
this.remove = function(element) {
let currentNode = head
let previousNode
if (currentNode.element !== element) {
head = currentNode.next
} else {
while (currentNode.element !== element) {
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
}
this.isEmpty = function() {
return length === 0
}
this.indexOf = function(element) {
let currentNode = head
let index = -1
while (currentNode) {
index++
if (currentNode.element === element) {
return index
}
currentNode = currentNode.next
}
return -1
}
this.elementAt = function(index) {
let currentNode = head
let count = 0
while (count < index) {
count++
currentNode = currentNode.next
}
return currentNode.element
}
this.addAt = function(index, element) {
let node = new Node(element)
let currentNode = head
let previousNode
let currentIndex = 0
if (index > length) return false
if (index === 0) {
node.next = currentNode
head = node
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
node.next = currentNode
previousNode.next = node
}
length++
}
this.removeAt = function(index) {
let currentNode = head
let previousNode
let currentIndex = 0
if (index < 0 || index >= length) return null
if (index === 0) {
head = currentIndex.next
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
return currentNode.element
}
}
4. Collection (de valeurs) (Set)
Une collection (plusieurs) est l'un des concepts de base des mathématiques: un ensemble d'objets bien définis et isolés. ES6 a introduit une collection qui ressemble quelque peu à un tableau. Cependant, la collection ne permet pas l'inclusion d'éléments en double et ne contient pas d'index.La collection standard comprend les méthodes suivantes:- valeurs: renvoyer tous les éléments de la collection
- taille: retourne le nombre d'éléments
- a: vérifier si un article est dans la collection
- ajouter: ajouter un élément
- supprimer: supprimer un élément
- union: retourne la zone d'intersection de deux collections
- différence: renvoyer les différences entre les deux collections
- sous-ensemble: vérifier si une collection est un sous-ensemble d'une autre
function MySet() {
let collection = []
this.has = function(element) {
return (collection.indexOf(element) !== -1)
}
this.values = function() {
return collection
}
this.size = function() {
return collection.length
}
this.add = function(element) {
if (!this.has(element)) {
collection.push(element)
return true
}
return false
}
this.remove = function(element) {
if (this.has(element)) {
index = collection.indexOf(element)
collection.splice(index, 1)
return true
}
return false
}
this.union = function(otherSet) {
let unionSet = new MySet()
let firstSet = this.values()
let secondSet = otherSet.values()
firstSet.forEach(i => unionSet.add(i))
secondSet.forEach(i => unionSet.add(i))
}
this.intersection = function(otherSet) {
let intersectionSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (otherSet.has(e)) {
intersectionSet.add(e)
}
})
return intersectionSet
}
this.difference = function(otherSet) {
let differenceSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (!otherSet.has(e)) {
differenceSet.add(e)
}
})
return differenceSet
}
this.subset = function(otherSet) {
lat firstSet = this.values()
return firstSet.every(value => otherSet.has(value))
}
}
5. Table de hachage (table de hachage)
Une table de hachage est une structure de données qui est construite sur une base clé-valeur. En raison de la vitesse élevée de recherche de valeurs par clé, il est utilisé dans des structures telles que Carte, Dictionnaire et Objet. Comme le montre la figure, la table de hachage a une fonction de hachage qui convertit les clés en une liste de nombres qui sont utilisés comme noms (valeurs) des clés. Le temps de recherche de la valeur clé peut atteindre O (1). Les clés identiques doivent renvoyer la même valeur - c'est l'essence même de la fonction de hachage.Une table de hachage a les méthodes suivantes:- add: ajouter une paire clé / valeur
- supprimer: supprimer une paire
- recherche: recherche de valeur par clé
function hash(string, max) {
let hash = 0
for (let i = 0; i < string.length; i++) {
hash += string.charCodeAt(i)
}
return hash % max
}
function HashTable() {
let storage = []
const storageLimit = 4
this.add = function(key, value) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
storage[index] = [
[key, value]
]
} else {
let inserted = false
for (let i = 0; i < storage[index].len; i++) {
if (storage[index][i][0] === key) {
storage[index][i][1] = value
inserted = true
}
}
if (inserted === false) {
storage[index].push([key, value])
}
}
}
this.remove = function(key) {
let index = hash(key, storageLimit)
if (storage[index].length === 1 && storage[index][0][0] === key) {
delete storage[index]
} else {
for (let i = 0; i < storage[index]; i++) {
if (storage[index][i][0] === key) {
delete storage[index][i]
}
}
}
}
this.lookup = function(key) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
return undefined
} else {
for (let i = 0; i < storage[index].length; i++) {
if (storage[index][i][0] === key) {
return storage[index][i][1]
}
}
}
}
}
6. Arbre
Une arborescence est une structure multicouche (multi-niveaux). Il s'agit également d'une structure non linéaire, contrairement à un tableau, une pile et une file d'attente. Cette structure est très efficace en termes d'ajout et de recherche d'éléments. Voici quelques concepts de structure arborescente:- root: élément racine, n'a pas de parent
- nœud parent: un nœud direct de la couche supérieure (niveau), il ne peut y en avoir qu'un
- nœud enfant: nœud (s) direct (s) du niveau inférieur, il peut y en avoir plusieurs
- frères et sœurs: enfants d'un nœud parent
- feuille: nœud sans "enfants"
- Edge: branche ou lien (lien) entre les nœuds
- Chemin: chemin (ensemble de liens) du nœud de départ à l'élément cible
- Hauteur de l'arbre: le nombre de liens du chemin le plus long d'un élément spécifique vers un nœud qui n'a pas d'enfants
- Profondeur du nœud: nombre de liens entre le nœud racine et un élément spécifique.
- Degré de nœud: nombre de descendants
Voici un exemple d'arbre de recherche binaire (BST). Chaque nœud n'a que deux enfants, le nœud gauche (enfant) est plus petit que le nœud actuel (parent), celui de droite est plus grand: Les
méthodes de cet arbre sont les suivantes:- ajouter: ajouter un nœud
- findMin: obtenir le nœud minimum
- findMax: obtenir le nœud maximum
- find: rechercher un nœud spécifique
- isPresent: rechercher un nœud spécifique
- supprimer: supprimer le nœud
class Node {
constructor(data, left = null, right = null) {
this.data = data
this.left = left
this.right = right
}
}
class BST {
constructor() {
this.root = null
}
add(data) {
const node = this.root
if (node === null) {
this.root = new Node(data)
return
} else {
const searchTree = function(node) {
if (data < node.data) {
if (node.left === null) {
node.left = new Node(data)
return
} else if (node.left !== null) {
return searchTree(node.left)
}
} else if (data > node.data) {
if (node.right === null) {
node.right = new Node(data)
return
} else if (node.right !== null) {
return searchTree(node.right)
}
} else {
return null
}
}
return searchTree(node)
}
}
findMin() {
let current = this.root
while (current.left !== null) {
current = current.left
}
return current.data
}
findMax() {
let current = this.root
while (current.right !== null) {
current = current.right
}
return current.data
}
find(data) {
let current = this.root
while (current.data !== data) {
if (data < current.data) {
current = current.left
} else {
current = current.right
}
if (current === null) {
return null
}
}
return current
}
isPresent(data) {
let current = this.root
while (current) {
if (data === current.data) {
return true
}
data < current.data ? current = current.left : current = current.right
}
return false
}
remove(data) {
const removeNode = function(node, data) {
if (node === null) return null
if (data === node.data) {
if (node.left === null && node.right === null) return null
if (node.left === null) return node.right
if (node.right === null) return node.left
let tempNode = node.right
while (tempNode.left !== null) {
tempNode = tempNode.left
}
node.data = tempNode.data
node.right = removeNode(node.right, tempNode.data)
return node
} else if (data < node.data) {
node.left = removeNode(node.right, data)
return node
} else {
node.right = removeNode(node.right, data)
return node
}
}
this.root = removeNode(this.root, data)
}
}
Essai:const bst = new BST()
bst.add(4)
bst.add(2)
bst.add(6)
bst.add(1)
bst.add(3)
bst.add(5)
bst.add(7)
bst.remove(4)
console.log(bst.findMin())
console.log(bst.findMax())
bst.remove(7)
console.log(bst.findMax())
console.log(bst.isPresent(4))
RĂ©sultat:1
7
6
false
7. Arbre chargé (préfixe) (Trie, lu comme "essayer")
L'arbre des préfixes est un type d'arbre de recherche. Les données qu'il contient sont stockées séquentiellement (étape par étape) - chaque nœud d'arbre représente une étape. L'arbre des préfixes est utilisé dans les dictionnaires, car il accélère considérablement la recherche.Chaque nœud d'arbre est une lettre de l'alphabet, suivre une branche conduit à la formation d'un mot. Il contient également un «indicateur booléen» pour déterminer que le nœud actuel est la dernière lettre.L'arbre des préfixes a les méthodes suivantes:- ajouter: ajouter un mot au dictionnaire
- isWord: recherchez un mot
- imprimer: renvoyer tous les mots
function Node() {
this.keys = new Map()
this.end = false
this.setEnd = function() {
this.end = true
}
this.isEnd = function() {
return this.end
}
}
function Trie() {
this.root = new Node()
this.add = function(input, node = this.root) {
if (input.length === 0) {
node.setEnd()
return
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node())
return this.add(input.substr(1), node.key.get(input[0]))
} else {
return this.add(input.substr(1), node.keys.get(input[0]))
}
}
this.isWord = function(word) {
let node = this.root
while (word.length > 1) {
if (node.keys.has(word[0])) {
return false
} else {
node = node.keys.get(word[0])
word = word.substr(1)
}
}
return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false
}
this.print = function() {
let words = new Array()
let search = function(node = this.root, string) {
if (node.keys.size !== 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter))
}
if (node.isEnd()) {
words.push(string)
}
} else {
string.length > 0 ? words.push(string) : undefined
return
}
}
search(this.root, new String())
return words.length > 0 ? words : null
}
}
8. Le graphique (graphique) (graphique)
Un graphique, également appelé réseau, est un ensemble de nœuds interconnectés. Il existe deux types de graphiques: orientés et non orientés, selon que les liens ont une direction. Les graphiques sont utilisés partout, par exemple, pour calculer le meilleur itinéraire dans les applications de navigation ou pour créer une liste de recommandations sur les réseaux sociaux.Les graphiques peuvent être présentés sous forme de liste ou de matrice.liste
Dans ce cas, tous les nœuds parents sont situés à gauche et leurs enfants à droite.
La matrice
Dans ce cas, les nœuds sont répartis en lignes et en colonnes, l'intersection de la ligne et de la colonne montre la relation entre les nœuds: 0 signifie que les nœuds ne sont pas connectés, 1 - les nœuds sont connectés.
Le graphique est recherché par deux méthodes: la recherche en largeur d'abord (Breath-First-Search, BFS) et la recherche en profondeur (Depth-First-Search, DFS).Considérez BFS:function bfs(graph, root) {
let nodesLen = {}
for (let i = 0; i < graph.length; i++) {
nodesLen[i] = Infinity
}
nodesLen[root] = 0
let queue = [root]
let current
while (queue.length !== 0) {
current = queue.shift()
let curConnected = graph[current]
let neighborIdx = []
let idx = curConnected.indexOf(1)
while (idx !== -1) {
neighborIdx.push(idx)
idx = curConnected.indexOf(1, idx + 1)
}
for (let i = 0; i < neighborIdx.length; i++) {
if (nodesLen[neighborIdx[i]] === Infinity) {
nodesLen[neighborIdx[i]] = nodesLen[current] + 1
queue.push(neighborIdx[i])
}
}
}
return nodesLen
}
Essai:let graph = [
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 0, 0]
]
console.log(bfs(graph, 1))
RĂ©sultat:{
0: 2,
1: 0,
2: 1,
3: 3,
4: Infinity
}
C’est tout pour moi. J'espère que vous trouverez quelque chose d'utile pour vous. Bon codage!