F #, algorithme de marquage pour les composants d'image connectés

La recherche et le marquage de composants connectés dans des images binaires est l'un des algorithmes de base pour l'analyse et le traitement d'images. En particulier, cet algorithme peut être utilisé en vision industrielle pour rechercher et compter des structures communes dans l'image, avec leur analyse ultérieure.

Dans le cadre de cet article, deux algorithmes de marquage des composants connectés seront considérés, leur implémentation dans le langage de programmation F # est montrée. Et aussi, une analyse comparative des algorithmes, la recherche de faiblesses. Le matériel source pour la mise en œuvre des algorithmes est tiré du livre " Computer Vision" (auteurs L. Shapiro, J. Stockman. Traduction de l'anglais par A. A. Boguslavsky édité par S. M. Sokolov) .

introduction

Un composant connecté avec une valeur de v est un ensemble de C tels pixels qui ont une valeur de v et chaque paire de ces pixels est connectée avec une valeur de v

Cela semble abstrus, alors voyons simplement l'image. Nous supposons que les pixels de premier plan de l'image binaire sont marqués comme 1 et les pixels d'arrière-plan sont marqués comme 0 .

Après avoir traité l'image avec l'algorithme de marquage des composants connectés, nous obtenons l'image suivante. Ici, au lieu de pixels, des composants connectés sont formés, qui diffèrent les uns des autres en nombre. Dans cet exemple, 5 composants ont été trouvés et il sera possible de travailler avec eux comme avec des entités distinctes.

Figure 1: Composants connectés étiquetés

$$

$$\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 2 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 2 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 \\ 3 & 3 & 3 & 3 & 0 & 4 & 0 & 2 \\ 0 & 0 & 0 & 3 & 0 & 4 & 0 & 2 \\ 5 & 5 & 0 & 3 & 0 & 0 & 0 & 2 \\ 5 & 5 & 0 & 3 & 0 & 2 & 2 & 2 \end{matrix}$$

Deux algorithmes pouvant être utilisés pour résoudre un tel problème seront examinés ci-dessous.

Algorithme d'étiquetage récursif

Nous commencerons par regarder l'algorithme basé sur la récursivité comme le plus évident. Le principe de fonctionnement d'un tel algorithme sera le suivant:

Attribuer une étiquette, dont nous marquerons les composants liés, la valeur initiale.

1. Nous trions tous les points du tableau, en commençant par la coordonnée 0x0 (coin supérieur gauche). Après avoir traité le point suivant, augmentez l'étiquette d'une unité
2. Si le pixel à la coordonnée actuelle est 1 , alors nous balayons les quatre voisins de ce point (haut, bas, droite, gauche)
3. Si le point voisin est également 1 , la fonction s'appelle récursivement pour traiter le voisin jusqu'à ce qu'il atteigne la limite du tableau ou du point 0
4. Lors du traitement récursif du voisin, il faut vérifier que le point n'a pas déjà été traité et est marqué avec le marqueur courant.

Ainsi, en triant tous les points du tableau et en invoquant un algorithme récursif pour chacun, puis à la fin de la recherche, nous obtenons un tableau entièrement marqué. Puisqu'il est vérifié si un point donné a déjà été marqué, chaque point ne sera traité qu'une seule fois. La profondeur de récursivité dépendra uniquement du nombre de voisins connectés au point actuel. Cet algorithme est bien adapté aux images qui n'ont pas un remplissage d'image volumineux. Autrement dit, des images dans lesquelles il y a des lignes fines et courtes, et tout le reste est une image d'arrière-plan qui n'est pas traitée. De plus, la vitesse d'un tel algorithme peut être supérieure à l'algorithme ligne par ligne (nous en parlerons plus loin dans l'article).

Étant donné que les images binaires bidimensionnelles sont des matrices bidimensionnelles, lors de l'écriture de l'algorithme, j'opérerai avec les concepts de matrices, dont j'ai fait un article séparé, que vous pouvez lire ici.

Programmation fonctionnelle en utilisant l'exemple de travail avec des matrices de la théorie de l'algèbre linéaire.

Considérez et analysez en détail la fonction F # qui implémente algorithme d'étiquetage récursif pour les composants d'image binaire connectés

let recMarkingOfConnectedComponents matrix =

        let copy = Matrix.clone matrix

        let (|Value|Zero|Out|) (x, y) = 
            if x < 0 || y < 0
                || x > (copy.values.[0, *].Length - 1)
                || y > (copy.values.[*, 0].Length - 1) then
                Out
            else
                let row = copy.values.[y, *]
                match row.[x] with
                    | 0 -> Zero
                    | v -> Value(v)

        let rec markBits x y value =
            match (x, y) with
            | Value(v) ->
                if value > v then
                    copy.values.[y, x] <- value
                    markBits (x + 1) y value
                    markBits (x - 1) y value
                    markBits x (y + 1) value
                    markBits x (y - 1) value
            | Zero | Out -> ()

        let mutable value = 2
        copy.values
        |> Array2D.iteri (fun y x v -> if v = 1 then
                                            markBits x y value
                                            value <- value + 1)

        copy 

Nous déclarons la fonction recMarkingOfConnectedComponents , qui prend un tableau matriciel bidimensionnel, compressé dans un enregistrement de type Matrix. La fonction ne changera pas le tableau d'origine, donc créez d'abord une copie de celui-ci, qui sera traitée par l'algorithme et retournée.

let copy = Matrix.clone matrix

Pour simplifier les vérifications des indices des points demandés en dehors du tableau, créez un modèle actif qui renvoie l'une des trois valeurs.

Out - l'index demandé est allé au-delà du tableau bidimensionnel
Zero - le point contient un pixel d'arrière-plan (égal à zéro)
Valeur - l'index demandé est dans le tableau

Ce modèle simplifiera la vérification des coordonnées du point d'image au cadre de récursivité suivant:

let (|Value|Zero|Out|) (x, y) = 
    if x < 0 || y < 0
        || x > (copy.values.[0, *].Length - 1)
        || y > (copy.values.[*, 0].Length - 1) then
        Out
    else
        let row = copy.values.[y, *]
        match row.[x] with
            | 0 -> Zero
            | v -> Value(v)

La fonction MarkBits est déclarée récursive et sert à traiter le pixel courant et tous ses voisins (haut, bas, gauche, droite):

let rec markBits x y value =
    match (x, y) with
    | Value(v) ->
        if value > v then
            copy.values.[y, x] <- value
            markBits (x + 1) y value
            markBits (x - 1) y value
            markBits x (y + 1) value
            markBits x (y - 1) value
    | Zero | Out -> ()

La fonction accepte les paramètres suivants en entrée:

x - numéro de ligne
y -
valeur de numéro de colonne - valeur d' étiquette actuelle pour marquer le pixel

En utilisant la construction match / with et le modèle actif (ci-dessus), les coordonnées des pixels sont vérifiées afin qu'elles ne dépassent pas la dimension bidimensionnelle tableau. Si le point se trouve à l'intérieur d'un tableau à deux dimensions, nous effectuons une vérification préliminaire afin de ne pas traiter le point qui a déjà été traité.

if value > v then

Sinon, une récursion infinie se produira et l'algorithme ne fonctionnera pas.

Ensuite, marquez le point avec la valeur actuelle du marqueur:

copy.values.[y, x] <- value

Et nous traitons tous ses voisins, en appelant récursivement la même fonction:

markBits (x + 1) y value
markBits (x - 1) y value
markBits x (y + 1) value
markBits x (y - 1) value

Après avoir implémenté l'algorithme, il doit être utilisé. Considérez le code plus en détail.

let mutable value = 2
copy.values
|> Array2D.iteri (fun y x v -> if v = 1 then
                                    markBits x y value
                                    value <- value + 1) 

Avant de traiter l'image, définissez la valeur initiale de l'étiquette, qui marquera les groupes de pixels connectés.

let mutable value = 2

Le fait est que les pixels avant de l'image binaire sont déjà définis sur 1 , donc si la valeur initiale de l'étiquette est également 1 , l'algorithme ne fonctionnera pas. Par conséquent, la valeur initiale de l'étiquette doit être supérieure à 1 . Il existe une autre façon de résoudre le problème. Avant de démarrer l'algorithme, marquez tous les pixels définis sur 1 avec une valeur initiale de -1 . Ensuite, nous pouvons définir la valeur sur 1 . Vous pouvez le faire vous-même si vous le souhaitez.

La construction suivante, à l'aide de la fonction Array2D.iteri , itère sur tous les points du tableau et si, pendant la recherche, vous rencontrez un point défini sur 1, cela signifie qu'il n'est pas traité et pour cela, vous devez appeler la fonction récursive markBits avec la valeur d'étiquette actuelle. Tous les pixels définis sur 0 sont ignorés par l'algorithme.

Après avoir traité récursivement le point, nous pouvons supposer que l'ensemble du groupe connecté auquel ce point appartient est garanti d'être marqué et vous pouvez augmenter la valeur d'étiquette de 1 pour l'appliquer au prochain point connecté.

Prenons un exemple d'application d'un tel algorithme.

let a = array2D [[1;1;0;1;1;1;0;1]
                 [1;1;0;1;0;1;0;1]
                 [1;1;1;1;0;0;0;1]
                 [0;0;0;0;0;0;0;1]
                 [1;1;1;1;0;1;0;1]
                 [0;0;0;1;0;1;0;1]
                 [1;1;0;1;0;0;0;1]
                 [1;1;0;1;0;1;1;1]]
let A = Matrix.ofArray2D a

let t = System.Diagnostics.Stopwatch.StartNew()
let R = Algorithms.recMarkingOfConnectedComponents A
t.Stop()

printfn "origin =\n %A" A.values
printfn "rec markers =\n %A" R.values
printfn "elapsed recurcive = %O" t.Elapsed 

origin =
 [[1; 1; 0; 1; 1; 1; 0; 1]
 [1; 1; 0; 1; 0; 1; 0; 1]
 [1; 1; 1; 1; 0; 0; 0; 1]
 [0; 0; 0; 0; 0; 0; 0; 1]
 [1; 1; 1; 1; 0; 1; 0; 1]
 [0; 0; 0; 1; 0; 1; 0; 1]
 [1; 1; 0; 1; 0; 0; 0; 1]
 [1; 1; 0; 1; 0; 1; 1; 1]]

rec markers =
 [[2; 2; 0; 2; 2; 2; 0; 3]
 [2; 2; 0; 2; 0; 2; 0; 3]
 [2; 2; 2; 2; 0; 0; 0; 3]
 [0; 0; 0; 0; 0; 0; 0; 3]
 [4; 4; 4; 4; 0; 5; 0; 3]
 [0; 0; 0; 4; 0; 5; 0; 3]
 [6; 6; 0; 4; 0; 0; 0; 3]
 [6; 6; 0; 4; 0; 3; 3; 3]]

elapsed recurcive = 00:00:00.0037342

Les avantages d'un algorithme récursif incluent sa simplicité d'écriture et de compréhension. Il est idéal pour les images binaires contenant un grand arrière-plan et entrecoupées de petits groupes de pixels (par exemple, des lignes, des petits points, etc.). Dans ce cas, la vitesse de traitement d'image peut être élevée, car l'algorithme traite l'image entière en une seule passe.

Les inconvénients sont également évidents - c'est la récursivité. Si l'image se compose de grandes taches ou est complètement inondée, la vitesse de traitement diminue fortement (par ordre de grandeur) et il y a un risque que le programme plante du tout en raison du manque d'espace libre sur la pile.

Malheureusement, le principe de la récursion de queue ne peut pas être appliqué dans cet algorithme, car la récursivité de queue a deux exigences:

1. Chaque trame de récursivité doit effectuer des calculs et ajouter le résultat à l'accumulateur, qui sera transmis dans la pile.
2. Il ne doit pas y avoir plus d'un appel de fonction récursive dans une trame de récursivité.

Dans notre cas, la récursivité n'effectue aucun calcul final, qui peut être passé à la trame de récursivité suivante, mais modifie simplement un tableau à deux dimensions. En principe, cela pourrait être contourné en renvoyant simplement un numéro unique, ce qui en soi ne signifie rien. Nous effectuons également 4 appels récursivement, car nous devons traiter les quatre voisins du point.

Algorithme classique pour marquer les composants connectés en fonction de la structure des données pour combiner les recherches

L'algorithme a également un autre nom, «Algorithme de marquage progressif», et ici nous allons essayer de l'analyser.

. . . , , .

La définition ci-dessus est encore plus confuse, nous allons donc essayer de traiter le principe de l'algorithme d'une manière différente et partir de loin.

Tout d'abord, nous traiterons de la définition d'un voisinage à quatre et à huit connexions du point courant. Regardez les photos ci-dessous pour comprendre ce que c'est et quelle est la différence.

Figure 2: Le composant à quatre connexions
\ begin {matrix} Figure 2: Le composant à huit connexions \ begin {matrix} La première image montre un composant à quatre connexions $$\begin{matrix} & 1 & \\ 2 & * & 3 \\ & 4 & \end{matrix}$$


$$\begin{matrix} 1 & 2 & 3 \\ 4 & * & 5 \\ 6 & 7 & 8 \end{matrix}$$
c'est-à-dire que cela signifie que l'algorithme traite 4 voisins du point actuel (gauche, droite, haut et bas). Par conséquent, le composant à huit points d' un point signifie qu'il a 8 voisins. Dans cet article, nous allons travailler avec quatre composants connectés.

Maintenant, vous devez comprendre ce qu'est une structure de données pour combiner la recherche , construite sur certains ensembles?

Par exemple, supposons que nous ayons deux ensembles

$$

$$(1, 2, 3, 4, 8) (5, 6, 7)$$

Ces ensembles sont organisés sous la forme des arbres suivants: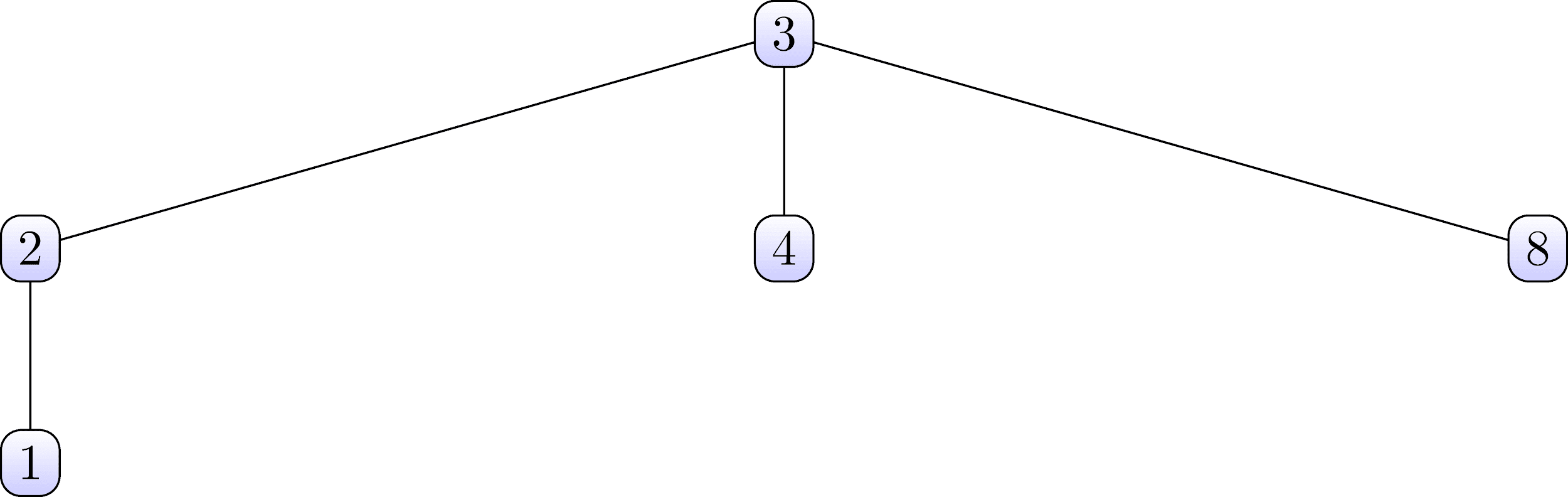





Notez que dans le premier ensemble, les nœuds 3 sont racine et dans le second, les nœuds 6.

Maintenant, nous considérons la structure de données pour une union de recherche, qui contient ces deux ensembles, et organise également leur structure arborescente .

Figure 4: Structure des données pour l'union de recherche
\ begin {matrix} Examinez attentivement le tableau ci-dessus et essayez de trouver une relation avec les arbres définis ci-dessus. Le tableau doit être affiché dans des colonnes verticales. C'est vu,que le chiffre 3 de la première ligne correspond au chiffre 0 $$\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 2 & 3 & 0 & 3 & 7 & 7 & 0 & 3 \end{matrix}$$

dans la deuxième ligne. Et dans le premier arbre, le nombre 3 est la racine du premier ensemble. Par analogie, vous pouvez constater que le numéro 7 de la première ligne correspond au numéro 0 de la deuxième ligne. Le nombre 7 est également la racine de l'arbre du deuxième ensemble.

Ainsi, nous concluons que les nombres de la ligne supérieure sont les nœuds filles des ensembles, et les nombres correspondants de la ligne inférieure sont leurs nœuds parents. Guidé par cette règle, vous pouvez facilement restaurer les deux arbres à partir du tableau ci-dessus.

Nous analysons ces détails afin que plus tard il nous soit plus facile de comprendre le fonctionnement de l'algorithme de marquage progressif .. Pour l'instant, attardons-nous sur le fait qu'une série de nombres de la première ligne est toujours des nombres de 1 à un certain nombre maximum. En fait, le nombre maximal de la première ligne est la valeur maximale des étiquettes avec lesquelles les composants connectés trouvés seront marqués . Et les ensembles individuels sont des transitions entre des étiquettes qui se forment à la suite de la première passe (nous examinerons plus en détail plus loin).

Avant de continuer, considérez le pseudo-code de certaines fonctions qui seront utilisées par l'algorithme.

Nous désignons le tableau représentant la structure de données pour la recherche de jointure comme PARENT . La fonction suivante est appelée find et prendra le libellé actuel X comme paramètreset un tableau de PARENT . Cette procédure trace les pointeurs parents jusqu'à la racine de l'arbre et trouve l'étiquette du nœud racine de l'arbre auquel X appartient .

 ̆   ̆  .
X —  
PARENT — , ̆    -

procedure find(X, PARENT);
{
j := X;
while PARENT[j] <> 0
    j := PARENT[j]; return(j);
}

Considérez comment une telle fonction peut être implémentée sur F #

let rec find x =
    let index = Array.tryFindIndex ((=)x) parents.[0, *]
    match index with
    | Some(i) -> 
        match parents.[1, i] with
        | p when p <> 0 -> find p
        | _ -> x
    | None -> x 

Nous déclarons ici une fonction récursive de la découverte , qui prend l'étiquette actuelle X . Le tableau PARRENT n'est pas passé ici, car nous l'avons déjà dans l'espace de noms global et la fonction le voit déjà et peut fonctionner avec.

Tout d'abord, la fonction essaie de trouver l'index de l'étiquette sur la ligne supérieure (puisque vous devez trouver son parent, qui se trouve sur la ligne inférieure.

let index = Array.tryFindIndex ((=)x) parents.[0, *]

Si la recherche réussit, nous obtenons son parent et comparons avec 0 . Si le parent n'est pas égal à 0 , ce nœud a également un parent et la fonction s'appelle récursivement jusqu'à ce que le parent soit égal à 0 . Cela signifie que nous avons trouvé le nœud racine de l'ensemble.

match index with
    | Some(i) -> 
        match parents.[1, i] with
        | p when p <> 0 -> find p
        | _ -> x
    | None -> x 

La fonction suivante dont nous avons besoin est appelée union . Il faut deux étiquettes X et Y , ainsi qu'un tableau de PARENT . Cette structure modifie (si nécessaire) PARENT de sous - ensembles de fusion contenant une étiquette X , avec l'ensemble comprenant l' étiquette Y . La procédure recherche les nœuds racine des deux étiquettes et s'ils ne correspondent pas, le nœud de l'une des étiquettes est désigné comme nœud parent de la deuxième étiquette. Il y a donc une union de deux ensembles.

   .
X — ,   .
Y — ,   .
PARENT — , ̆    -.

procedure union(X, Y, PARENT);
{
j := X;
k := Y;
while PARENT[j] <> 0
    j := PARENT[j];
while PARENT[k]] <> 0
    k := PARENT[k];

if j <> k then PARENT[k] := j;
} 

L'implémentation F # ressemble à ceci

let union x y =
    let j = find x
    let k = find y
    if j <> k then parents.[1, k-1] <- j 

Notez que la fonction de recherche que nous avons déjà implémentée est déjà utilisée ici .

L'algorithme nécessite également deux fonctions supplémentaires, appelées voisins et étiquettes . La fonction voisins renvoie l'ensemble des points voisins à gauche et en haut (puisque dans notre cas, l'algorithme fonctionne sur un composant à quatre connexions) à partir du pixel donné, et la fonction étiquettes renvoie l'ensemble d'étiquettes déjà attribuées à l'ensemble donné de pixels que la fonction voisins a renvoyé . Dans notre cas, nous n'implémenterons pas ces deux fonctions, mais nous n'en créerons qu'une qui combine les deux fonctions et renvoie les étiquettes trouvées.

let neighbors_labels x y =
    match (x, y) with
    | (0, 0) -> []
    | (0, _) -> [step1.[0, y-1]]
    | (_, 0) -> [step1.[x-1, 0]]
    | _ -> [step1.[x, y-1]; step1.[x-1, y]]
    |> List.filter ((<>)0) 

Pour l'avenir, je dirai tout de suite que le tableau step1 qui utilise la fonction existe déjà dans l'espace global et contient le résultat du traitement de l'algorithme lors de la première passe. Je veux porter une attention particulière au filtre supplémentaire.

|> List.filter ((<>)0)

Il coupe tous les résultats qui sont 0 . Autrement dit, si l'étiquette contient 0 , alors nous avons affaire à un point de l'image d'arrière-plan qui n'a pas besoin d'être traité. C'est une nuance très importante qui n'est pas mentionnée dans le livre, dont nous prenons des exemples, mais néanmoins, l'algorithme ne fonctionnera pas sans une telle vérification.

Petit à petit, étape par étape, nous nous rapprochons de l'essence même de l'algorithme. Regardons à nouveau l'image que nous devrons traiter.

Figure 5: Image binaire d'origine
\ begin {matrix} $$\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 & 1 & 1 \end{matrix}$$

Avant le traitement, créez un tableau vide step1 , dans lequel le résultat de la première passe sera enregistré.

Figure 6: Matrice étape 1 pour stocker les résultats du traitement principal
\ begin {matrix} $$\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

Considérez les premières étapes du traitement des données primaires (uniquement les trois premières lignes de l'image binaire d'origine).

Avant de jeter un œil pas à pas à l'algorithme, regardons le pseudo-code qui explique le principe général de fonctionnement.

     .
B —   .
LB —   .

procedure classical_with_union-find(B, LB);
{
“  .” initialize();
“  1 ̆  L     .”
for L := 0 to MaxRow
{
“     L  ”
for P := 0 to MaxCol
    LB[L,P] := 0;
“  L.”
for P := 0 to MaxCol
    if B[L,P] == 1 then
    {
        A := prior_neighbors(L,P);
        if isempty(A)
        then {M := label; label := label + 1;};
        else M := min(labels(A));
        LB[L,P] := M;
        for X in labels(A) and X <> M
           union(M, X, PARENT);
    }
}
“  2 ,    1,     .”
for L := 0 to MaxRow
    for P := 0 to MaxCol
        if B[L, P] == 1
        then LB[L,P] := find(LB[L,P], PARENT);
};
      LB ( step1)     ( ).

Figure 7: Étape 1. Point (0,0), label = 1
Figure 8: Étape 2. Point (1, 0), étiquette = 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Figure 9: Étape 2. Point (2.0), étiquette = 1 1 1 $$\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

$$\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

$$\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$
Figure 10: Étape 4. Point (3.0), étiquette = 2
$$\begin{matrix} 1 & 1 & 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$
Figure 11: Dernière étape, résultat final de la première passe
$$\begin{matrix} 1 & 1 & 0 & 2 & 2 & 2 & 0 & 3 \\ 1 & 1 & 0 & 2 & 0 & 2 & 0 & 3 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\ 4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\ 0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 7 & 7 & 3 \end{matrix}$$
Veuillez noter qu'à la suite du traitement initial de l'image d'origine, nous avons obtenu deux ensembles

$$

$$(1,2) - (3,7)$$

Visuellement, cela peut être vu comme le contact des marques 1 et 2 (coordonnées des points (1,3) et (2,3) ) et des marques 3 et 7 (coordonnées des points (7,7) et (7,6) ). Du point de vue de la structure de données pour la recherche-union, ce résultat est obtenu.

Figure 12: Structure de données calculée pour l'agrégation de recherche
$$\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 0 & 1 & 0 & 0 & 0 & 0 & 3 \end{matrix}$$
Après avoir finalement traité l'image en utilisant la structure de données obtenue, nous obtenons le résultat suivant.

Figure 13: Résultat final
$$\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 3 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 3 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\ 4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\ 0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 3 & 3 & 3 \end{matrix}$$
Maintenant, tous les composants connectés que nous avons ont des étiquettes uniques et peuvent être utilisés dans des algorithmes de traitement ultérieurs.

L'implémentation du code F # est la suivante

let markingOfConnectedComponents matrix =

    // up to 10 markers
    let parents = Array2D.init 2 10 (fun x y -> if x = 0 then y+1 else 0)

    // create a zero initialized copy
    let step1 = (Matrix.cloneO matrix).values

    let rec find x =
        let index = Array.tryFindIndex ((=)x) parents.[0, *]
        match index with
        | Some(i) -> 
            match parents.[1, i] with
            | p when p <> 0 -> find p
            | _ -> x
        | None -> x

    let union x y =
        let j = find x
        let k = find y
        if j <> k then parents.[1, k-1] <- j

    // returns up and left neighbors of pixel
    let neighbors_labels x y =
        match (x, y) with
        | (0, 0) -> []
        | (0, _) -> [step1.[0, y-1]]
        | (_, 0) -> [step1.[x-1, 0]]
        | _ -> [step1.[x, y-1]; step1.[x-1, y]]
        |> List.filter ((<>)0)

    let mutable label = 0
    matrix.values
    |> Array2D.iteri (fun x y v ->
                        if v = 1 then
                            let n = neighbors_labels x y
                            let m = if n.IsEmpty then
                                        label <- label + 1
                                        label
                                    else
                                        n |> List.min
                            n |> List.iter (fun v -> if v <> m then union m v)
                            step1.[x, y] <- m)

    let step2 = matrix.values
                |> Array2D.mapi (fun x y v ->
                        if v = 1 then step1.[x, y] <- find step1.[x, y]
                        step1.[x, y])

    { values = step2 } 

Une explication ligne par ligne du code n'a plus de sens, car tout a été décrit ci-dessus. Ici, vous pouvez simplement mapper le code F # au pseudo-code pour clarifier son fonctionnement.

Algorithmes d'analyse comparative

Comparons la vitesse de traitement des données avec les deux algorithmes (récursif et par ligne).

let a = array2D [[1;1;0;1;1;1;0;1]
                 [1;1;0;1;0;1;0;1]
                 [1;1;1;1;0;0;0;1]
                 [0;0;0;0;0;0;0;1]
                 [1;1;1;1;0;1;0;1]
                 [0;0;0;1;0;1;0;1]
                 [1;1;0;1;0;0;0;1]
                 [1;1;0;1;0;1;1;1]]
let A = Matrix.ofArray2D a

let t1 = System.Diagnostics.Stopwatch.StartNew()
let R1 = Algorithms.markingOfConnectedComponents A
t1.Stop()

let t2 = System.Diagnostics.Stopwatch.StartNew()
let R2 = Algorithms.recMarkingOfConnectedComponents A
t2.Stop()

printfn "origin =\n %A" A.values
printfn "markers =\n %A" R1.values
printfn "rec markers =\n %A" R2.values

printfn "elapsed lines = %O" t1.Elapsed
printfn "elapsed recurcive = %O" t2.Elapsed 

origin =
 [[1; 1; 0; 1; 1; 1; 0; 1]
 [1; 1; 0; 1; 0; 1; 0; 1]
 [1; 1; 1; 1; 0; 0; 0; 1]
 [0; 0; 0; 0; 0; 0; 0; 1]
 [1; 1; 1; 1; 0; 1; 0; 1]
 [0; 0; 0; 1; 0; 1; 0; 1]
 [1; 1; 0; 1; 0; 0; 0; 1]
 [1; 1; 0; 1; 0; 1; 1; 1]]
markers =
 [[1; 1; 0; 1; 1; 1; 0; 3]
 [1; 1; 0; 1; 0; 1; 0; 3]
 [1; 1; 1; 1; 0; 0; 0; 3]
 [0; 0; 0; 0; 0; 0; 0; 3]
 [4; 4; 4; 4; 0; 5; 0; 3]
 [0; 0; 0; 4; 0; 5; 0; 3]
 [6; 6; 0; 4; 0; 0; 0; 3]
 [6; 6; 0; 4; 0; 3; 3; 3]]
rec markers =
 [[2; 2; 0; 2; 2; 2; 0; 3]
 [2; 2; 0; 2; 0; 2; 0; 3]
 [2; 2; 2; 2; 0; 0; 0; 3]
 [0; 0; 0; 0; 0; 0; 0; 3]
 [4; 4; 4; 4; 0; 5; 0; 3]
 [0; 0; 0; 4; 0; 5; 0; 3]
 [6; 6; 0; 4; 0; 0; 0; 3]
 [6; 6; 0; 4; 0; 3; 3; 3]]
elapsed lines = 00:00:00.0081837
elapsed recurcive = 00:00:00.0038338

Comme vous pouvez le voir, dans cet exemple, la vitesse de l'algorithme récursif dépasse considérablement la vitesse de l'algorithme ligne par ligne. Mais tout change dès que nous commençons à traiter une image remplie de couleur unie et pour plus de clarté, nous allons également augmenter sa taille à 100x100 pixels.

let a = Array2D.create 100 100 1
let A = Matrix.ofArray2D a

let t1 = System.Diagnostics.Stopwatch.StartNew()
let R1 = Algorithms.markingOfConnectedComponents A
t1.Stop()
printfn "elapsed lines = %O" t1.Elapsed

let t2 = System.Diagnostics.Stopwatch.StartNew()
let R2 = Algorithms.recMarkingOfConnectedComponents A
t2.Stop()
printfn "elapsed recurcive = %O" t2.Elapsed 

elapsed lines = 00:00:00.0131790
elapsed recurcive = 00:00:00.2632489

Comme vous pouvez le voir, l'algorithme récursif est déjà 25 fois plus lent que l'algorithme linéaire. Augmentons la taille de l'image à 200x200 pixels.

elapsed lines = 00:00:00.0269896
elapsed recurcive = 00:00:06.1033132

La différence est déjà plusieurs centaines de fois. Je note que déjà à une taille de 300x300 pixels, l'algorithme récursif provoque un débordement de pile et le programme plante.

Sommaire

Dans le cadre de cet article, l'un des algorithmes de base pour marquer les composants connectés pour le traitement des images binaires a été examiné en utilisant le langage fonctionnel F # comme exemple. Ici ont été donnés des exemples de mise en œuvre d'algorithmes récursifs et classiques, leur principe de fonctionnement a été expliqué, une analyse comparative a été faite à l'aide d'exemples spécifiques.

Le code source discuté ici peut également être consulté sur le
github MatrixAlgorithms.J'espère

que cet article était intéressant pour ceux intéressés par F # et les algorithmes de traitement d'image en particulier.