🤵🏻 🔦 👩🏼‍🍳 Prédiction de séries chronologiques à l'aide de réseaux de neurones récurrents 👨‍🎤 👑 💞

Le mode de fonctionnement à distance dans le contexte de l'auto-isolation universelle peut entraîner de très graves conséquences. Et l'épuisement émotionnel - c'est toujours partout où il va: là, après tout, ce n'est pas loin du toit. À cet égard, comme beaucoup, il a essayé de se "calmer" en allouant du temps à d'autres classes - et a commencé à traduire les articles les plus intéressants de l'anglais vers le russe: "Vous donnez un apprentissage automatique aux masses!".) Nous devons rendre hommage: c'est très distrayant. Si vous avez des suggestions pour le contenu sémantique et la traduction de ce texte pour un lecteur russophone, rejoignez la discussion.

Voici donc une traduction de la page de prévision des séries chronologiques de la section du manuel tensorflow: lien . Mes ajouts ainsi que des illustrations pour la traduction visent à aider à comprendre les idées de base dans l'un des domaines les plus intéressants du ML et de l'économétrie en général - la prévision des séries chronologiques.

Une petite introduction avant la traduction.

Le manuel est une description de la prévision de la température de l'air basée sur des séries chronologiques unidimensionnelles ( séries chronologiques univariées) et des séries chronologiques multivariées ( séries chronologiques multivariées) . Pour chaque partie, saisissez les donnéesdoivent être préparés en conséquence. En tenant compte de l'ensemble de données météorologiques considéré dans ce guide, la séparation est la suivante: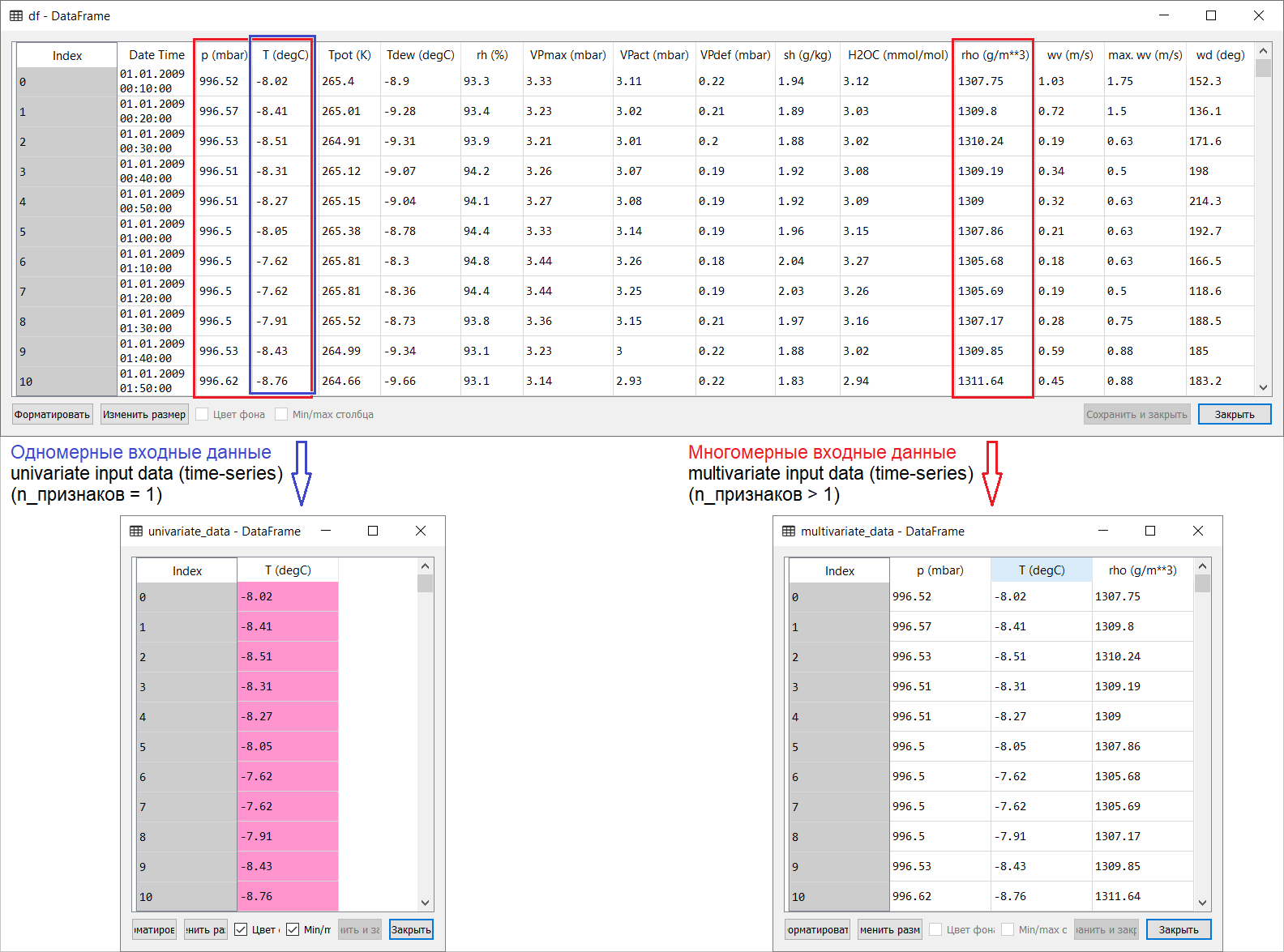

pour les questions sur ce qu'il faut prendre pour X et ce pour Y , c'est-à-dire comment préparer les données pour la classe de formation supervisée, il deviendra clair à partir des illustrations suivantes. Je note seulement que la formation du vecteur cible (Y) pour travailler avec des séries temporelles à la fois unidimensionnelles et multidimensionnelles est la même: le vecteur cible est compilé sur la base du signe T (degC)(température de l'air). La différence entre eux est «enfouie» dans la formation d'un ensemble de caractéristiques qui sont introduites dans l'entrée du modèle: dans le cas d'une série chronologique unidimensionnelle pour prédire la température dans le futur, le vecteur d'entrée (X) se compose d'une caractéristique: en fait, la température de l'air; et pour plusieurs dimensions - plusieurs: en plus de la température de l'air, p (mbar) (pression atmosphérique) et rho (g / m ** 3) (humidité) sont utilisés dans l'exemple du manuel en question .

Au début, très superficiel, un exemple avec la prévision de température ne semble pas convaincant du point de vue de l'utilisation d'une entrée multidimensionnelle: pour prévoir la température, le signe le plus pertinent sera la température. Mais ce n'est absolument pas le cas: pour développer une prévision qualitative de la température de l'air, de nombreux facteurs doivent être pris en compte, jusqu'au frottement de l'air à la surface de la terre, etc. De plus, en pratique, certaines choses sont loin d'être évidentes, et le vecteur cible peut être sous la forme de ce méli-mélo (ou bortsch). À cet égard, l'analyse des données exploratoires avec la sélection des caractéristiques les plus pertinentes pour la formation ultérieure d'une entrée multidimensionnelle est la seule bonne décision.

Ainsi, la traduction du manuel est présentée ci-dessous. Le texte supplémentaire sera en italique .

Prévision de séries chronologiques

Ce guide est une introduction à la prévision de séries chronologiques à l'aide de réseaux de neurones récurrents (RNS, de l'anglais Recurrent Neural Network, RNN ). Il se compose de deux parties: la première décrit la prévision de la température de l'air sur la base d'une série chronologique unidimensionnelle et la seconde - sur la base d'une série chronologique multidimensionnelle.

import tensorflow as tf

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd

mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False

Un ensemble de données météorologiques

Tous les exemples de séquences temporelles d' utilisation manuelle de données météorologiques enregistrées dans une station hydrométéorologique de l' Institut de biogéochimie nommé d'après Max Planck .

Cet ensemble de données comprend des mesures de 14 indicateurs météorologiques différents (tels que la température de l'air, la pression atmosphérique, l'humidité), effectuées toutes les 10 minutes depuis 2003. Pour économiser du temps et de la mémoire, le manuel utilisera des données couvrant la période de 2009 à 2016. Cette section de l'ensemble de données a été préparée par François Chollet pour son livre, Deep Learning with Python .

zip_path = tf.keras.utils.get_file(
    origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
    fname='jena_climate_2009_2016.csv.zip',
    extract=True)
csv_path, _ = os.path.splitext(zip_path)

df = pd.read_csv(csv_path)

Voyons voir ce que nous avons.

df.head()

Le fait que la période d'enregistrement d'observation soit de 10 minutes peut être vérifié par le tableau ci-dessus. Ainsi, en une heure vous aurez 6 observations. À son tour, 144 observations (6x24) sont accumulées par jour.

Disons que vous voulez prédire la température, qui sera dans 6 heures dans le futur. Vous faites cette prévision sur la base des données dont vous disposez pour une certaine période: par exemple, vous décidez d'utiliser 5 jours d'observation. Par conséquent, pour former le modèle, vous devez créer un intervalle de temps contenant les 720 dernières observations (5x144) (puisque différentes configurations sont possibles, cet ensemble de données est une bonne base pour les expériences).

La fonction ci-dessous renvoie les intervalles de temps ci-dessus pour l'apprentissage du modèle. Argumenthistory_size- c'est la taille du dernier intervalle de temps, target_size- un argument qui détermine jusqu'où le modèle devrait apprendre à prédire. En d'autres termes, target_sizec'est le vecteur cible qui doit être prédit.

def univariate_data(dataset, start_index, end_index, history_size, target_size):
  data = []
  labels = []

  start_index = start_index + history_size
  if end_index is None:
    end_index = len(dataset) - target_size

  for i in range(start_index, end_index):
    indices = range(i-history_size, i)
    # Reshape data from (history_size,) to (history_size, 1)
    data.append(np.reshape(dataset[indices], (history_size, 1)))
    labels.append(dataset[i+target_size])
  return np.array(data), np.array(labels)

Dans les deux parties du manuel, les 300 000 premières lignes de données seront utilisées pour former le modèle, les autres pour le valider (valider). Dans ce cas, la quantité de données d'entraînement est d'environ 2100 jours.

TRAIN_SPLIT = 300000

Pour garantir des résultats reproductibles, la fonction d'amorçage est définie.

tf.random.set_seed(13)

Partie 1. Prévision basée sur une série chronologique unidimensionnelle

Dans la première partie, vous formerez le modèle en utilisant un seul attribut - température; le modèle formé sera utilisé pour prévoir les températures futures.

Pour commencer, nous extrayons uniquement la température de l'ensemble de données.

uni_data = df['T (degC)']
uni_data.index = df['Date Time']
uni_data.head()

Date Time
01.01.2009 00:10:00 -8.02
01.01.2009 00:20:00 -8.41
01.01.2009 00:30:00 -8.51
01.01.2009 00:40:00 -8.31
01.01.2009 00:50:00 -8.27
Name: T (degC), dtype: float64

Et voyons comment ces données changent au fil du temps.

uni_data.plot(subplots=True)

uni_data = uni_data.values

Avant de former un réseau neuronal artificiel (ci-après - ANN), une étape importante est la mise à l'échelle des données. L'un des moyens courants d'effectuer la mise à l'échelle est la standardisation ( standardisation ), effectuée en soustrayant la moyenne et en divisant par l'écart-type pour chaque caractéristique. Vous pouvez également utiliser une méthode tf.keras.utils.normalizequi met les valeurs à l'échelle dans la plage [0,1].

Remarque : la normalisation ne doit être effectuée qu'en utilisant les données de formation.

uni_train_mean = uni_data[:TRAIN_SPLIT].mean()
uni_train_std = uni_data[:TRAIN_SPLIT].std()

Nous effectuons la standardisation des données.

uni_data = (uni_data-uni_train_mean)/uni_train_std

Ensuite, nous préparerons les données pour le modèle avec une entrée unidimensionnelle. Les 20 dernières observations enregistrées de la température seront transmises à l'entrée du modèle, et le modèle doit être formé pour prédire la température au prochain pas de temps.

univariate_past_history = 20
univariate_future_target = 0

x_train_uni, y_train_uni = univariate_data(uni_data, 0, TRAIN_SPLIT,
                                           univariate_past_history,
                                           univariate_future_target)
x_val_uni, y_val_uni = univariate_data(uni_data, TRAIN_SPLIT, None,
                                       univariate_past_history,
                                       univariate_future_target)

Les résultats de l'application de la fonction univariate_data.

print ('Single window of past history')
print (x_train_uni[0])
print ('\n Target temperature to predict')
print (y_train_uni[0])

Single window of past history
[[-1.99766294]
[-2.04281897]
[-2.05439744]
[-2.0312405 ]
[-2.02660912]
[-2.00113649]
[-1.95134907]
[-1.95134907]
[-1.98492663]
[-2.04513467]
[-2.08334362]
[-2.09723778]
[-2.09376424]
[-2.09144854]
[-2.07176515]
[-2.07176515]
[-2.07639653]
[-2.08913285]
[-2.09260639]
[-2.10418486]]

Target temperature to predict
-2.1041848598100876

Addition: la préparation des données pour un modèle avec une entrée unidimensionnelle est schématiquement illustrée dans la figure suivante (pour plus de commodité, dans cette figure et les suivantes, les données sont présentées sous une forme «brute», avant normalisation, et également sans l'attribut «Date heure» comme index):

Maintenant que les données convenablement préparé, considérez un exemple concret. Les informations transmises à l'ANN sont surlignées en bleu, une croix rouge indique la valeur future que l'ANN devrait prédire.

def create_time_steps(length):
  return list(range(-length, 0))

def show_plot(plot_data, delta, title):
  labels = ['History', 'True Future', 'Model Prediction']
  marker = ['.-', 'rx', 'go']
  time_steps = create_time_steps(plot_data[0].shape[0])
  if delta:
    future = delta
  else:
    future = 0

  plt.title(title)
  for i, x in enumerate(plot_data):
    if i:
      plt.plot(future, plot_data[i], marker[i], markersize=10,
               label=labels[i])
    else:
      plt.plot(time_steps, plot_data[i].flatten(), marker[i], label=labels[i])
  plt.legend()
  plt.xlim([time_steps[0], (future+5)*2])
  plt.xlabel('Time-Step')
  return plt

show_plot([x_train_uni[0], y_train_uni[0]], 0, 'Sample Example')

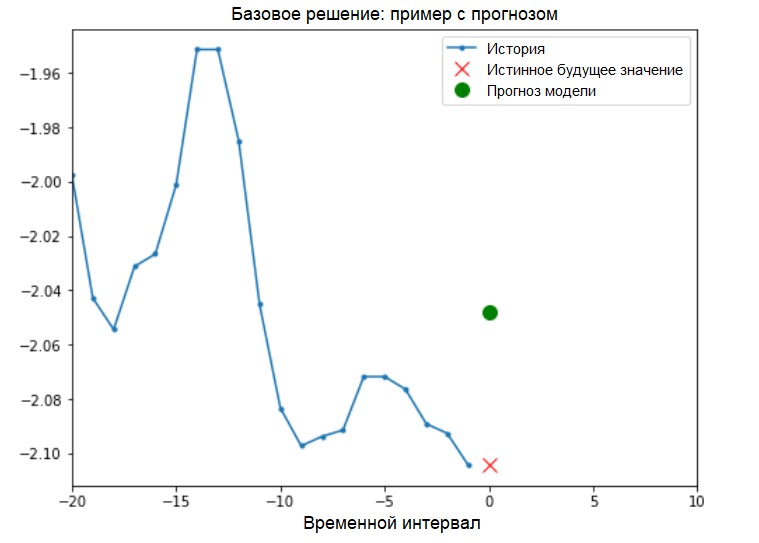
Solution de base (sans impliquer l'apprentissage automatique)

Avant de commencer la formation sur le modèle, nous allons installer une solution de base simple ( référence ). Elle consiste en ce qui suit: pour un vecteur d'entrée donné, la méthode de solution de base «scanne» tout l'historique et prédit la valeur suivante comme la moyenne des 20 dernières observations.

def baseline(history):
  return np.mean(history)

show_plot([x_train_uni[0], y_train_uni[0], baseline(x_train_uni[0])], 0,
           'Baseline Prediction Example')

Voyons voir si nous pouvons dépasser le résultat de la «moyenne» en utilisant un réseau de neurones récurrent.

Réseau

neuronal récurrent Un réseau neuronal récurrent (RNS) est un type d'ANN qui convient bien à la résolution de problèmes de séries chronologiques. Le RNS traite pas à pas la séquence temporelle des données, trie ses éléments et préserve l'état interne obtenu en traitant les éléments précédents. Vous pouvez trouver plus d'informations sur RNS dans le guide suivant . Ce guide utilisera une couche spécialisée de RNC appelée mémoire à court terme à long terme ( LSTM ).

Utilisation ultérieuretf.dataMélangez, regroupez et mettez en cache l'ensemble de données.

Ajout:

Plus d'informations sur les méthodes de lecture aléatoire, de traitement par lots et de cache sur la page tensorflow :

BATCH_SIZE = 256
BUFFER_SIZE = 10000

train_univariate = tf.data.Dataset.from_tensor_slices((x_train_uni, y_train_uni))
train_univariate = train_univariate.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()

val_univariate = tf.data.Dataset.from_tensor_slices((x_val_uni, y_val_uni))
val_univariate = val_univariate.batch(BATCH_SIZE).repeat()

La visualisation suivante devrait vous aider à comprendre à quoi ressemblent les données après le traitement par lots.

On peut voir que LSTM nécessite une certaine forme de saisie de données qui lui est fournie.

simple_lstm_model = tf.keras.models.Sequential([
    tf.keras.layers.LSTM(8, input_shape=x_train_uni.shape[-2:]),
    tf.keras.layers.Dense(1)
])

simple_lstm_model.compile(optimizer='adam', loss='mae')

Vérifiez la sortie du modèle.

for x, y in val_univariate.take(1):
    print(simple_lstm_model.predict(x).shape)

(256, 1)

Addition:

En termes généraux, les RNS fonctionnent avec des séquences. Cela signifie que les données fournies à l'entrée du modèle doivent avoir la forme suivante:

[, , - ]
La forme des données d'apprentissage pour le modèle avec une entrée unidimensionnelle a la forme suivante:

print(x_train_uni.shape)
(299980, 20, 1)

Ensuite, nous étudierons le modèle. En raison de la grande taille de l'ensemble de données et afin de gagner du temps, chaque époque ne passera que par 200 étapes ( steps_per_epoch = 200 ) au lieu des données d'entraînement complètes, comme c'est généralement le cas.

EVALUATION_INTERVAL = 200
EPOCHS = 10

simple_lstm_model.fit(train_univariate, epochs=EPOCHS,
                      steps_per_epoch=EVALUATION_INTERVAL,
                      validation_data=val_univariate, validation_steps=50)

Train for 200 steps, validate for 50 steps
Epoch 1/10
200/200 [==============================] - 2s 11ms/step - loss: 0.4075 - val_loss: 0.1351
Epoch 2/10
200/200 [==============================] - 1s 4ms/step - loss: 0.1118 - val_loss: 0.0360
Epoch 3/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0490 - val_loss: 0.0289
Epoch 4/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0444 - val_loss: 0.0257
Epoch 5/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0299 - val_loss: 0.0235
Epoch 6/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0317 - val_loss: 0.0224
Epoch 7/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0287 - val_loss: 0.0206
Epoch 8/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0263 - val_loss: 0.0200
Epoch 9/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0254 - val_loss: 0.0182
Epoch 10/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0228 - val_loss: 0.0174

Prédiction à l'aide d'un modèle LSTM simple

Après avoir terminé la préparation d'un modèle LSTM simple, nous ferons plusieurs prédictions.

for x, y in val_univariate.take(3):
  plot = show_plot([x[0].numpy(), y[0].numpy(),
                    simple_lstm_model.predict(x)[0]], 0, 'Simple LSTM model')
  plot.show()

Il semble meilleur que le niveau de base.

Maintenant que vous vous êtes familiarisé avec les bases, passons à la deuxième partie, qui décrit l'utilisation d'une série chronologique multidimensionnelle.

Partie 2: Prévision multidimensionnelle des séries chronologiques

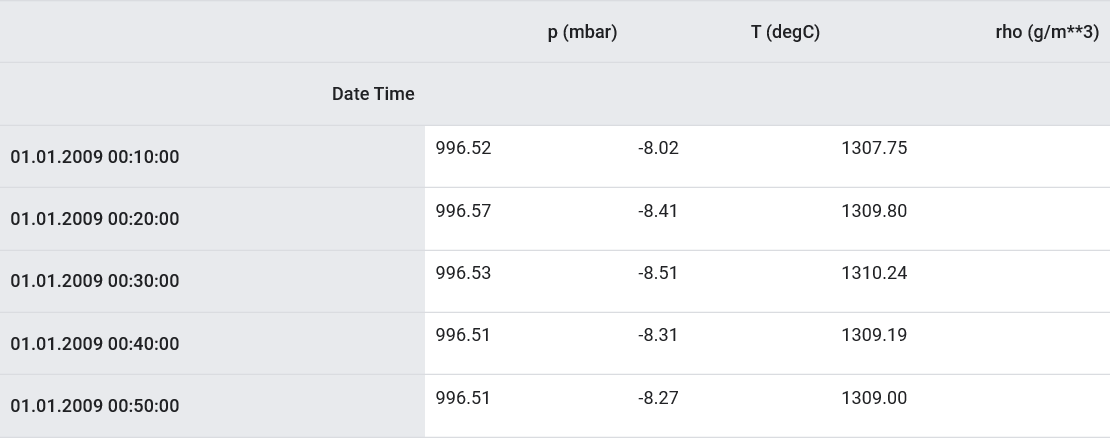
Comme indiqué, l'ensemble de données d'origine contient 14 indicateurs météorologiques différents. Pour plus de simplicité et de commodité, dans la deuxième partie, seuls trois d'entre eux sont pris en compte: la température de l'air, la pression atmosphérique et la densité de l'air.

Pour utiliser plus de fonctionnalités, leurs noms doivent être ajoutés à la liste feature_considered .

features_considered = ['p (mbar)', 'T (degC)', 'rho (g/m**3)']

features = df[features_considered]
features.index = df['Date Time']
features.head()

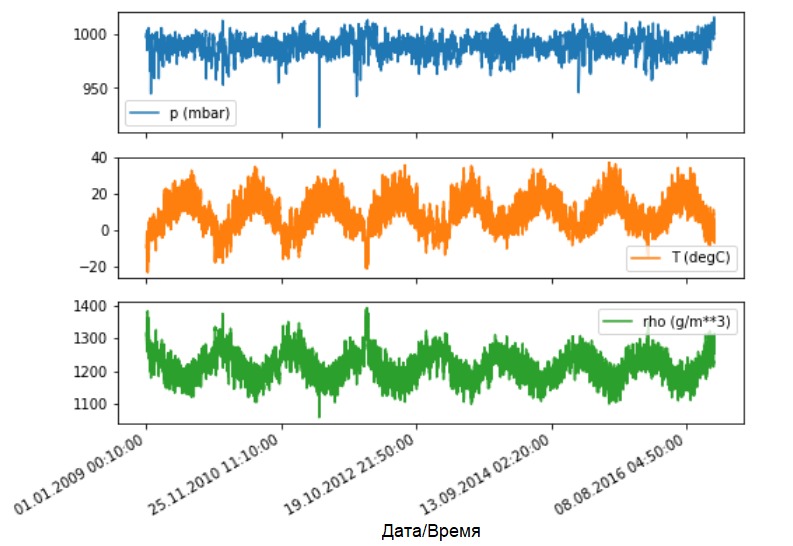
Voyons comment ces indicateurs changent au fil du temps.

features.plot(subplots=True)

Comme précédemment, la première étape consiste à standardiser l'ensemble de données avec le calcul de la valeur moyenne et l'écart type des données d'apprentissage.

dataset = features.values
data_mean = dataset[:TRAIN_SPLIT].mean(axis=0)
data_std = dataset[:TRAIN_SPLIT].std(axis=0)

dataset = (dataset-data_mean)/data_std

Addition:

Plus loin dans le manuel, nous parlerons de prévisions ponctuelles et d'intervalles.
Le résultat est le suivant. Si vous avez besoin du modèle pour prédire une valeur dans le futur (par exemple, la valeur de température après 12 heures) (modèle en une étape / en une seule étape), vous devez alors entraîner le modèle afin qu'il ne prédit qu'une seule valeur dans le futur. Si la tâche consiste à prédire la plage de valeurs à l'avenir (par exemple, les températures horaires au cours des 12 prochaines heures) (modèle à plusieurs étapes), le modèle doit également être formé pour prédire la plage de valeurs à l'avenir.

Prédiction ponctuelle

Dans ce cas, le modèle est formé pour prédire une valeur dans le futur en fonction de l'historique disponible.
La fonction ci-dessous effectue la même tâche d'organisation des intervalles de temps uniquement avec la différence qu'elle sélectionne ici les dernières observations en fonction d'une taille de pas donnée.

def multivariate_data(dataset, target, start_index, end_index, history_size,
                      target_size, step, single_step=False):
  data = []
  labels = []

  start_index = start_index + history_size
  if end_index is None:
    end_index = len(dataset) - target_size

  for i in range(start_index, end_index):
    indices = range(i-history_size, i, step)
    data.append(dataset[indices])

    if single_step:
      labels.append(target[i+target_size])
    else:
      labels.append(target[i:i+target_size])

  return np.array(data), np.array(labels)

Dans ce guide, l'ANN fonctionne sur les données des cinq (5) derniers jours, soit 720 observations (6x24x5). Supposons que la sélection des données soit effectuée non pas toutes les 10 minutes, mais toutes les heures: dans les 60 minutes, des changements brusques ne sont pas attendus. Par conséquent, l'histoire des cinq derniers jours comprend 120 observations (720/6). Pour un modèle qui effectue une prédiction ponctuelle, l'objectif est de lire la température après 12 heures à l'avenir. Dans ce cas, le vecteur cible sera la température après 72 (12x6) observations ( voir l'addition suivante. - Traducteur approx. ).

past_history = 720
future_target = 72
STEP = 6

x_train_single, y_train_single = multivariate_data(dataset, dataset[:, 1], 0,
                                                   TRAIN_SPLIT, past_history,
                                                   future_target, STEP,
                                                   single_step=True)
x_val_single, y_val_single = multivariate_data(dataset, dataset[:, 1],
                                               TRAIN_SPLIT, None, past_history,
                                               future_target, STEP,
                                               single_step=True)

Vérifiez l'intervalle de temps.

print ('Single window of past history : {}'.format(x_train_single[0].shape))

Single window of past history : (120, 3)

train_data_single = tf.data.Dataset.from_tensor_slices((x_train_single, y_train_single))
train_data_single = train_data_single.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()

val_data_single = tf.data.Dataset.from_tensor_slices((x_val_single, y_val_single))
val_data_single = val_data_single.batch(BATCH_SIZE).repeat()

single_step_model = tf.keras.models.Sequential()
single_step_model.add(tf.keras.layers.LSTM(32,
                                           input_shape=x_train_single.shape[-2:]))
single_step_model.add(tf.keras.layers.Dense(1))

single_step_model.compile(optimizer=tf.keras.optimizers.RMSprop(), loss='mae')

Nous vérifierons notre échantillon et en déduirons les courbes de perte aux étapes de la formation et de la vérification.

for x, y in val_data_single.take(1):
  print(single_step_model.predict(x).shape)

(256, 1)

single_step_history = single_step_model.fit(train_data_single, epochs=EPOCHS,
                                            steps_per_epoch=EVALUATION_INTERVAL,
                                            validation_data=val_data_single,
                                            validation_steps=50)

Train for 200 steps, validate for 50 steps
Epoch 1/10
200/200 [==============================] - 4s 18ms/step - loss: 0.3090 - val_loss: 0.2646
Epoch 2/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2624 - val_loss: 0.2435
Epoch 3/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2616 - val_loss: 0.2472
Epoch 4/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2567 - val_loss: 0.2442
Epoch 5/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2263 - val_loss: 0.2346
Epoch 6/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2416 - val_loss: 0.2643
Epoch 7/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2411 - val_loss: 0.2577
Epoch 8/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2410 - val_loss: 0.2388
Epoch 9/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2447 - val_loss: 0.2485
Epoch 10/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2388 - val_loss: 0.2422

def plot_train_history(history, title):
  loss = history.history['loss']
  val_loss = history.history['val_loss']

  epochs = range(len(loss))

  plt.figure()

  plt.plot(epochs, loss, 'b', label='Training loss')
  plt.plot(epochs, val_loss, 'r', label='Validation loss')
  plt.title(title)
  plt.legend()

  plt.show()

plot_train_history(single_step_history,
                   'Single Step Training and validation loss')

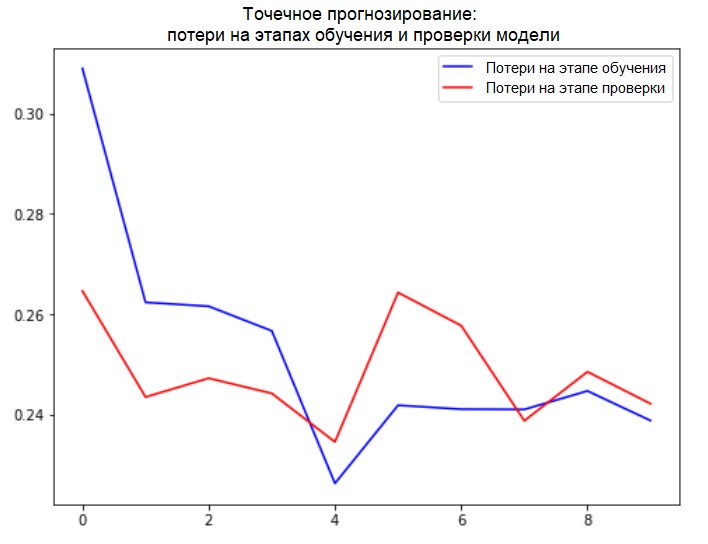Addition:

La préparation des données pour un modèle avec une entrée multidimensionnelle effectuant une prédiction ponctuelle est schématisée dans la figure suivante. Pour plus de commodité et une représentation plus visuelle de la préparation des données, l'argument STEPest 1. Notez que dans les fonctions de générateur données, l' argument est STEP destiné uniquement à la formation de l'historique , et non au vecteur cible.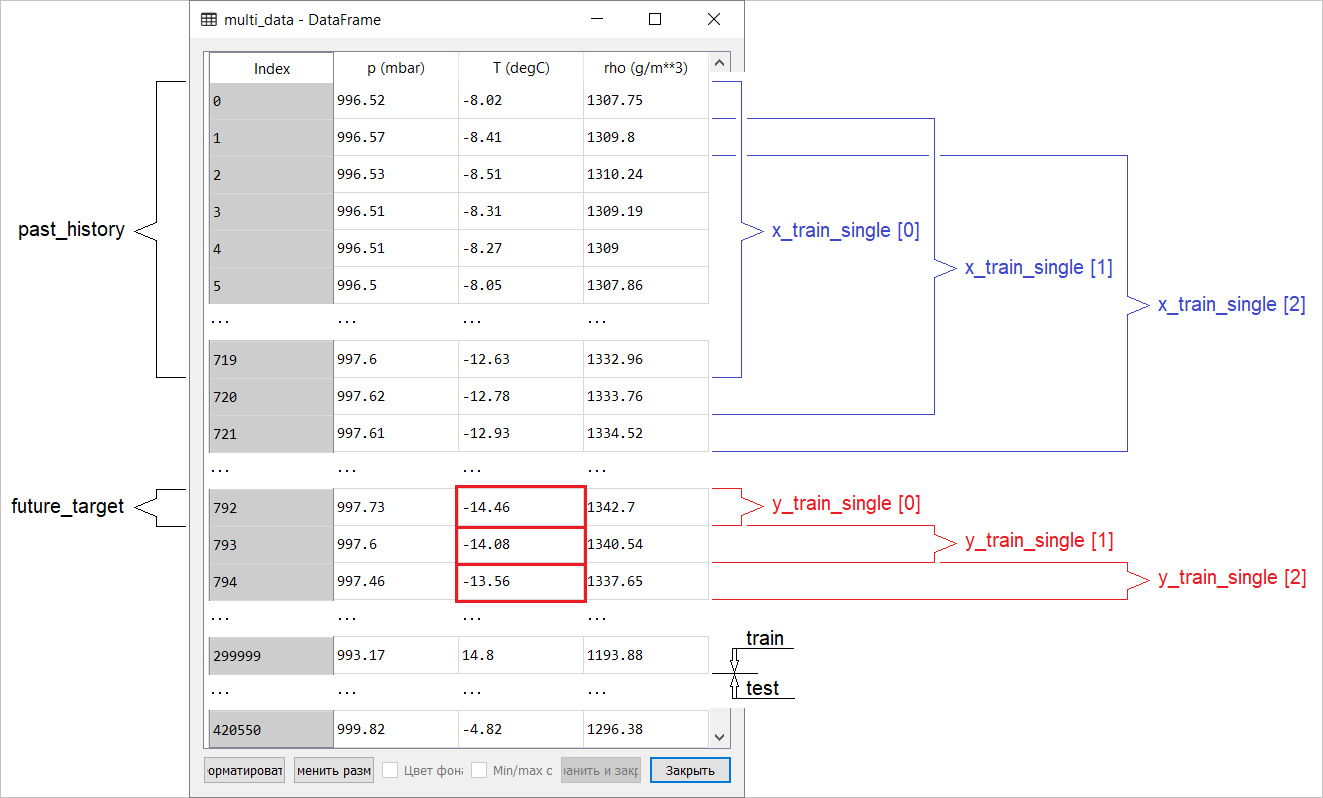

Dans ce cas, il x_train_singlea la forme (299280, 720, 3).
Quand STEP=6, le formulaire prendra la forme suivante: (299280, 120, 3)et la vitesse de la fonction augmentera considérablement. En général, il faut donner du crédit au programmeur: les générateurs présentés dans le manuel sont très voraces en termes de consommation mémoire.

Réalisation d'une prédiction ponctuelle

Maintenant que le modèle est formé, nous allons effectuer plusieurs prédictions de test. L'historique des observations de 3 signes pour les cinq derniers jours, sélectionnés toutes les heures (intervalle de temps = 120), est transmis à l'entrée du modèle. Puisque notre objectif est de prévoir uniquement la température, les valeurs de température passées ( historique ) sont affichées en bleu sur le graphique . La prévision a été faite une demi-journée dans le futur (d'où l'écart entre l'histoire et la valeur prédite).

for x, y in val_data_single.take(3):
  plot = show_plot([x[0][:, 1].numpy(), y[0].numpy(),
                    single_step_model.predict(x)[0]], 12,
                   'Single Step Prediction')
  plot.show()

Prévision d'intervalle

Dans ce cas, sur la base d'un historique disponible, le modèle est formé pour prédire l'intervalle des valeurs futures. Ainsi, contrairement à un modèle qui ne prédit qu'une seule valeur à l'avenir, ce modèle prédit une séquence de valeurs à l'avenir.

Supposons que, comme dans le cas du modèle effectuant la prédiction ponctuelle, pour le modèle effectuant la prédiction d'intervalle, les données d'apprentissage correspondent aux mesures horaires des cinq derniers jours (720/6). Cependant, dans ce cas, le modèle doit être formé pour prédire la température pour les 12 prochaines heures. Étant donné que les observations sont enregistrées toutes les 10 minutes, la sortie du modèle devrait consister en 72 prédictions. Pour terminer cette tâche, il est nécessaire de préparer à nouveau l'ensemble de données, mais avec un intervalle cible différent.

future_target = 72
x_train_multi, y_train_multi = multivariate_data(dataset, dataset[:, 1], 0,
                                                 TRAIN_SPLIT, past_history,
                                                 future_target, STEP)
x_val_multi, y_val_multi = multivariate_data(dataset, dataset[:, 1],
                                             TRAIN_SPLIT, None, past_history,
                                             future_target, STEP)

Vérifiez la sélection.

print ('Single window of past history : {}'.format(x_train_multi[0].shape))
print ('\n Target temperature to predict : {}'.format(y_train_multi[0].shape))

Single window of past history : (120, 3)

Target temperature to predict : (72,)

train_data_multi = tf.data.Dataset.from_tensor_slices((x_train_multi, y_train_multi))
train_data_multi = train_data_multi.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()

val_data_multi = tf.data.Dataset.from_tensor_slices((x_val_multi, y_val_multi))
val_data_multi = val_data_multi.batch(BATCH_SIZE).repeat()

Addition: la différence dans la formation du vecteur cible pour le «modèle d'intervalle» du «modèle ponctuel» est visible dans la figure suivante.

Nous préparerons la visualisation.

def multi_step_plot(history, true_future, prediction):
  plt.figure(figsize=(12, 6))
  num_in = create_time_steps(len(history))
  num_out = len(true_future)

  plt.plot(num_in, np.array(history[:, 1]), label='History')
  plt.plot(np.arange(num_out)/STEP, np.array(true_future), 'bo',
           label='True Future')
  if prediction.any():
    plt.plot(np.arange(num_out)/STEP, np.array(prediction), 'ro',
             label='Predicted Future')
  plt.legend(loc='upper left')
  plt.show()

Sur ce graphique et les graphiques similaires suivants, l'historique et les données futures sont horaires.

for x, y in train_data_multi.take(1):
  multi_step_plot(x[0], y[0], np.array([0]))

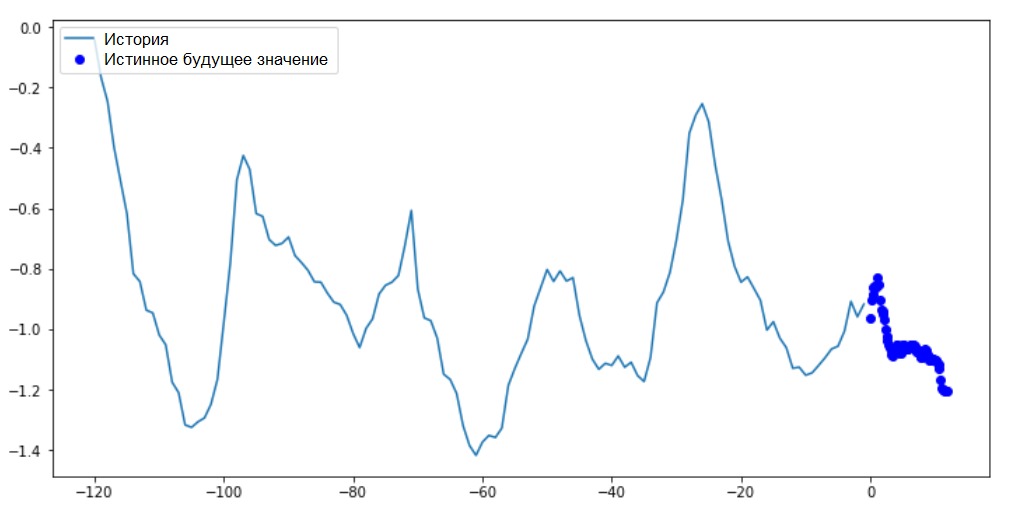Comme cette tâche est un peu plus compliquée que la précédente, le modèle consistera en deux couches LSTM. Enfin, puisque 72 prédictions sont effectuées, la couche de sortie comprend 72 neurones.

multi_step_model = tf.keras.models.Sequential()
multi_step_model.add(tf.keras.layers.LSTM(32,
                                          return_sequences=True,
                                          input_shape=x_train_multi.shape[-2:]))
multi_step_model.add(tf.keras.layers.LSTM(16, activation='relu'))
multi_step_model.add(tf.keras.layers.Dense(72))

multi_step_model.compile(optimizer=tf.keras.optimizers.RMSprop(clipvalue=1.0), loss='mae')

Nous vérifierons notre échantillon et en déduirons les courbes de perte aux étapes de la formation et de la vérification.

for x, y in val_data_multi.take(1):
  print (multi_step_model.predict(x).shape)

(256, 72)

multi_step_history = multi_step_model.fit(train_data_multi, epochs=EPOCHS,
                                          steps_per_epoch=EVALUATION_INTERVAL,
                                          validation_data=val_data_multi,
                                          validation_steps=50)

Train for 200 steps, validate for 50 steps
Epoch 1/10
200/200 [==============================] - 21s 103ms/step - loss: 0.4952 - val_loss: 0.3008
Epoch 2/10
200/200 [==============================] - 18s 89ms/step - loss: 0.3474 - val_loss: 0.2898
Epoch 3/10
200/200 [==============================] - 18s 89ms/step - loss: 0.3325 - val_loss: 0.2541
Epoch 4/10
200/200 [==============================] - 18s 89ms/step - loss: 0.2425 - val_loss: 0.2066
Epoch 5/10
200/200 [==============================] - 18s 89ms/step - loss: 0.1963 - val_loss: 0.1995
Epoch 6/10
200/200 [==============================] - 18s 90ms/step - loss: 0.2056 - val_loss: 0.2119
Epoch 7/10
200/200 [==============================] - 18s 91ms/step - loss: 0.1978 - val_loss: 0.2079
Epoch 8/10
200/200 [==============================] - 18s 89ms/step - loss: 0.1957 - val_loss: 0.2033
Epoch 9/10
200/200 [==============================] - 18s 90ms/step - loss: 0.1977 - val_loss: 0.1860
Epoch 10/10
200/200 [==============================] - 18s 88ms/step - loss: 0.1904 - val_loss: 0.1863

plot_train_history(multi_step_history, 'Multi-Step Training and validation loss')

Réalisation d'une prédiction d'intervalle

Alors, découvrons avec quel succès un ANN formé peut faire face aux prévisions des valeurs de température futures.

for x, y in val_data_multi.take(3):
  multi_step_plot(x[0], y[0], multi_step_model.predict(x)[0])

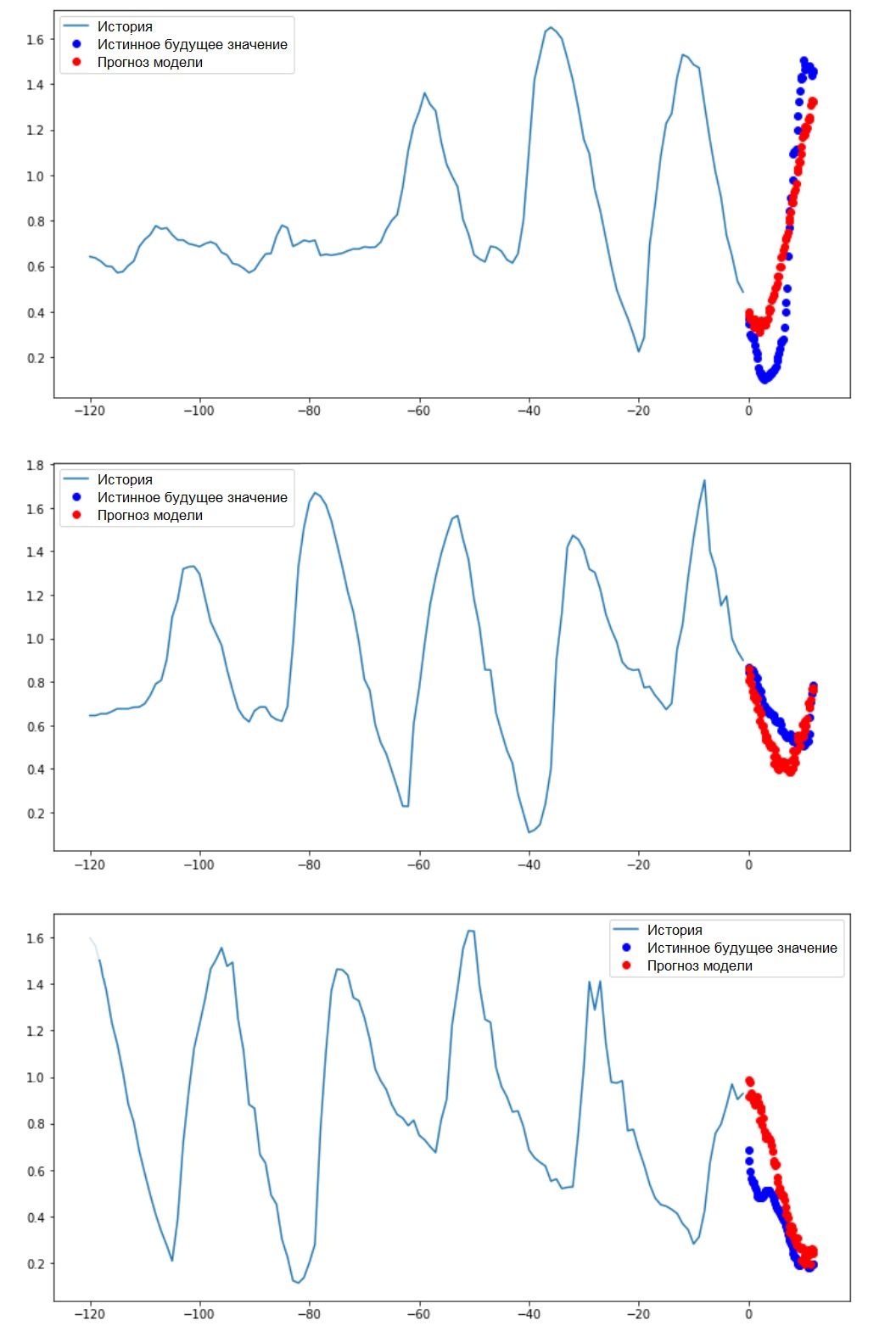
Prochaines étapes

Ce guide est une brève introduction à la prévision de séries chronologiques utilisant RNS. Maintenant, vous pouvez essayer de prédire le marché boursier et devenir milliardaire (dans l'original, juste comme ça :). - Remarque traducteur) .

De plus, vous pouvez écrire votre propre générateur pour préparer les données au lieu de la fonction uni / multivariate_data afin d'utiliser la mémoire plus efficacement. Vous pouvez également vous familiariser avec le travail de « fenêtrage de séries chronologiques » et apporter ses idées à ce guide.

Pour une meilleure compréhension, il est recommandé de lire le chapitre 15 du livre «Apprentissage automatique de la machine avec Scikit-Learn, Keras et TensorFlow» (Aurelien Geron, 2e édition) et le chapitre 6 du livre«Deep Learning in Python» (François Scholl).

Ajout final

Tout en restant à la maison, prenez soin non seulement de votre santé, mais prenez aussi pitié de l'ordinateur en exécutant des exemples du manuel sur un ensemble de données tronqué. Par exemple, en tenant compte de la proportion de 70x30 (formation / tests), vous pouvez la limiter comme suit:

dataset = features[300000:].values
TRAIN_SPLIT = 85000

Prédiction de séries chronologiques à l'aide de réseaux de neurones récurrents

Prévision de séries chronologiques

Partie 1. Prévision basée sur une série chronologique unidimensionnelle

Partie 2: Prévision multidimensionnelle des séries chronologiques

Prochaines étapes

More articles: