Les réseaux 8 bits sur Elbrus, est-ce logique?

Bonjour, Habr! Nous avons soudain réalisé que notre dernier article sur Elbrus est sorti il ​​y a un an. Nous avons donc décidé de corriger cet oubli gênant, car nous n'avons pas abandonné ce sujet!

Il est difficile d'imaginer la reconnaissance sans réseaux de neurones, nous allons donc parler de la façon dont nous avons lancé les grilles 8 bits sur Elbrus et de ce qui en est résulté. En général, un modèle avec des coefficients et entrées 8 bits et des calculs intermédiaires 32 bits est extrêmement populaire. Par exemple, Google [1] et Facebook [2] ont lancé leurs propres implémentations qui optimisent l'accès à la mémoire, utilisent SIMD et vous permettent d'accélérer les calculs de 25% ou plus sans diminution notable de la précision (cela dépend bien sûr de l'architecture du réseau de neurones et de la calculatrice, mais vous avez besoin on a expliqué à quel point c'était cool?).

 

L'idée de remplacer les nombres réels par des nombres entiers pour accélérer les calculs est dans l'air:

• . , “” , float , ;
• . - , , … , . , (SIMD). c 128- SIMD 4 float’ 16 uint8. 4 , ;
• , . — !

8- [3] . , , .

8- , 16-, . 32- . , 8- . , .

, — . (. . 1) :

$$

$$O(x, y, k) = \varphi(\sum_{c} \sum_{\Delta x} \sum_{\Delta y} I(c, x + \Delta x, y + \Delta y) w_k(c, \Delta x, \Delta y) + b_k) ~~~~~(1)$$

$$$(x, y)$— , $$$O$— , $$$I$— , $$$w_k$— .

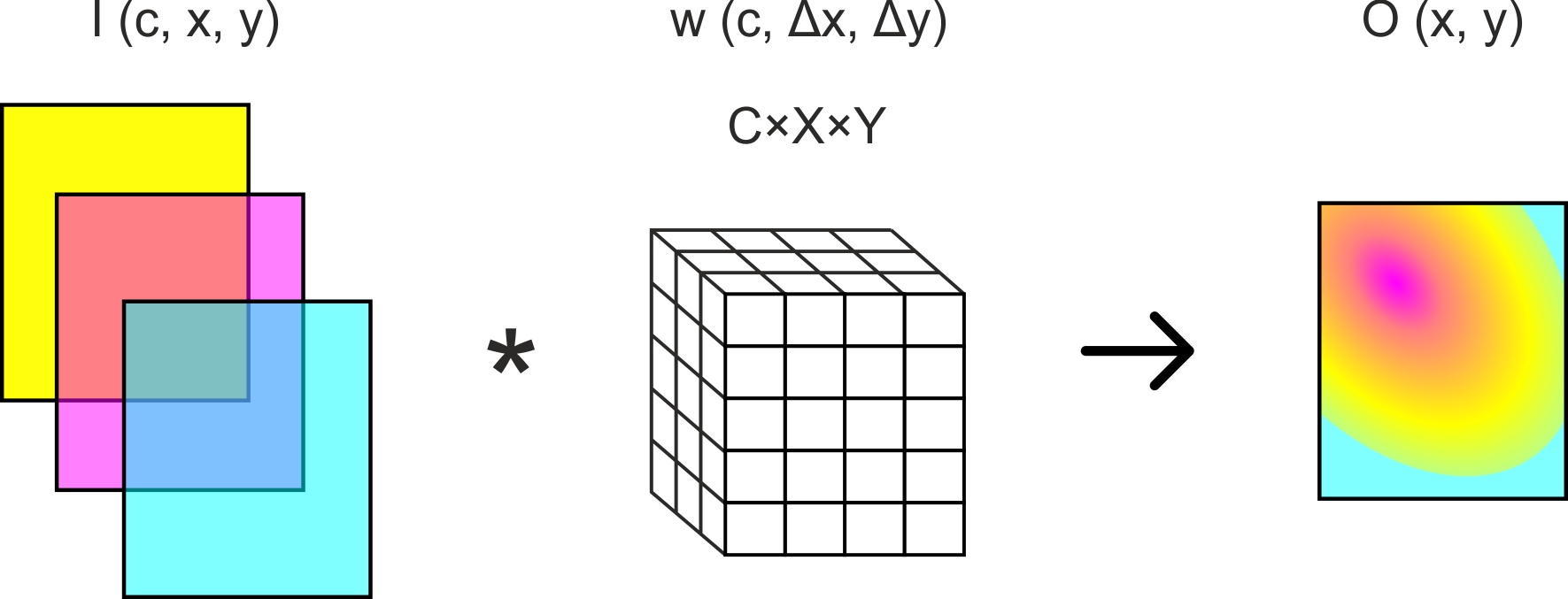
. 1. C x X x Y.

— [4]. , , . , "" — .. , . , .. (1). "" , .. ( ), ..

8- 32- .

- , , .

– , . , , — . . , , , [5-7].

6 ( ), . : - , . , , , , , . , .

. 1 (). 32 .

1. . "/" , , .

, - APB (array prefetch buffer). APB n- , . -, , APB , . APB :

• ;
• 3 4 APB , 5 ~6.

, APB :

• , APB;
• , 32b;
• , .

, , . , . Goto [8] . , , , . .

, , (. . 2-3). — . , .. . , APB - : , 8 ( 64- ) 2 .

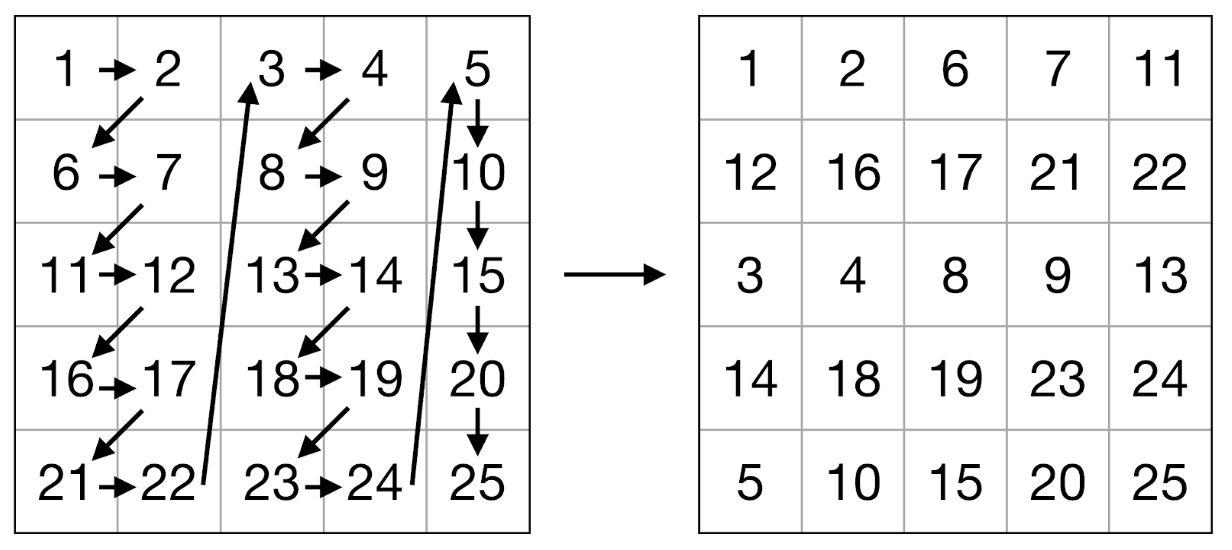
. 2. .

3. .

:

for bl_r in block_r(rhs):
  packed_r <- pack_rhs(bl_r)
  for bl_l in block_l(lhs):
    packed_l <- pack_lhs(bl_l)
    packed_res <- pack_res(bl_res)
    kernel(packed_res, packed_l, packed_r)
    bl_res <- unpack_res(packed_res)

lhs rhs — , block_l(.), block_r(.) — , lhs rhs . pack_rhs pack_lhs , pack_res — , unpack_res — . kernel .

kernel :

for j in {0, ..., cols / nr}
{dst0, dst1} <-   
  for i in {0, ..., rows / mr}
    for k in {0, ..., depth / 2}
      bl_r <-    
      bl_l <-    
      lhs <- pshufb(zero, bl_l, 0x0901080009010800LL)
      rhs0 <- punpcklbh(zero, bl_r)
      rhs1 <- punpckhbh(zero, bl_r)
      dst0 <- dst0 + pmaddh(rhs0, lhs)
      dst1 <- dst1 + pmaddh(rhs1, lhs);
//   

pshufb — , ( ), punpckhbh — , 16- , punpcklbh — , 16- , pmaddh — , 16- .

. nr mr = 12 8.

, 8 48 . 8 3, 14 , — 48 +, 8 .

2 8- -4, EML. N = 10^6 .

2. EML .

, -4 . , .

8- , x86 ARM, . , , , . 8- . , , ( , x86 ARM), : 6 64- , (64 128 ) 2 6 .

, 8- 32- . 3 (-4), 4 5 (-8 -8).

? , . , “” , . - , . , , / .

- 8- ? , , , - ( ).

P.S.
Limonova E. E., Neyman-Zade M. I., Arlazarov V. L. Special aspects of matrix operation implementations for low-precision neural network model on the Elbrus platform // . . — 2020. — . 13. — № 1. — . 118-128. — DOI: 10.14529/mmp200109.