Coderikune fois noté: "Il n'y a jamais trop de filtres Kalman . " On peut en dire autant du théorème de Bayes, car d'une part il est si simple, mais d'autre part il est si difficile d'en comprendre la profondeur.

YouTube a une merveilleuse chaîne Student Dave , mais la dernière vidéo a été publiée il y a six ans. La chaîne contient des vidéos éducatives dans lesquelles l'auteur raconte des choses complexes dans un langage très simple: théorème de Bayes, filtre de Kalman, etc. L'élève Dave complète son histoire avec un exemple de calcul en matlab.

Une fois sa leçon vidéo intitulée «Évaluation bayésienne itérative» m'a vraiment beaucoup aidé (sur la chaîne, cela correspond à la playlist «Estimation bayésienne itérative: avec MATLAB») Je voulais que tout le monde se familiarise avec les explications de Dave, mais malheureusement le projet n'est pas pris en charge. Dave lui-même ne prend pas contact. Vous ne pouvez pas ajouter de traduction à la vidéo, car elle doit être initiée par l'auteur lui-même. Contacter YouTube n'a pas donné de résultat, j'ai donc décidé de décrire le matériel dans un article en russe et de publier où il est le plus apprécié. Le matériel est très révisé et complété, car il est passé par ma perception subjective, donc le mettre en traduction serait inapproprié. Mais j'ai pris le sel même de l'explication de Dave. J'ai réécrit son code en python, car j'y travaille moi-même et le considère comme un bon substitut aux packages mathématiques.

Donc, si vous voulez approfondir le sujet du théorème de Bayes, bienvenue.

Formulation du problème

, “ ”. .

-, . , . , . . , . . - .

Si vous regardez la vidéo sur la chaîne, vous découvrirez que le ninja n'a pas réussi à sauter sur la caille, mais c'est une autre histoire.

- $x$ . $x = 3$ . . .

( ) $N = 100$ () .

$\sigma_y^2=4$ .
, .

f_{p o s t e r i o r} (x) = \frac{f_{p r i o r} (x) \cdot f_{и з м} (x)}{\int f_{p r i o r} (x) \cdot f_{m e s} (x) d x},

$\begin{equation} f_{posterior}(x) = \frac{f_{prior}(x) \cdot f_{}(x)}{\int f_{prior}(x) \cdot f_{mes}(x) dx}, \end{equation}$

$f_{posterior}(x)$ — ;
$f_{prior}(x)$ — ;
$f_{mes}(x)$ — ( $L_x(sample)$ ).
. , ( , ):

f_{m e s} (x) = p d f (x = y, μ = x, σ = σ) = \frac{1}{2 π σ} e^{- \frac{(y - x)^{2}}{2 σ^{2}}},

$\begin{equation} f_{mes}(x) =pdf(x=y, \mu=x, \sigma=\sigma) = \frac{1}{2 \pi \sigma} e^{- \frac{(y-x)^2}{2\sigma^2}}, \end{equation}$

$pdf$ — ;
$\mu$ — ;
$\sigma$ — ;
$y$ — .
( $N$ ), , .

.
$\sigma$ , 99,7 %.

- , .

. -.
$(3, 5)$ . ( ) .

() , . .

:

f_{p o s t e r i o r} (X) = \frac{f_{p r i o r} (X) \cdot f_{и з м} (X)}{\int f_{p r i o r} (X) \cdot f_{m e s} (X) d X},

$\begin{equation} f_{posterior}(X) = \frac{f_{prior}(X) \cdot f_{}(X)}{\int f_{prior}(X) \cdot f_{mes}(X) dX}, \end{equation}$

$X$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ ;
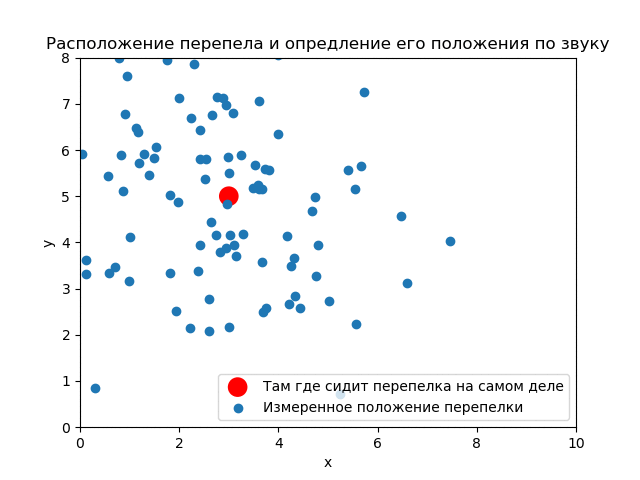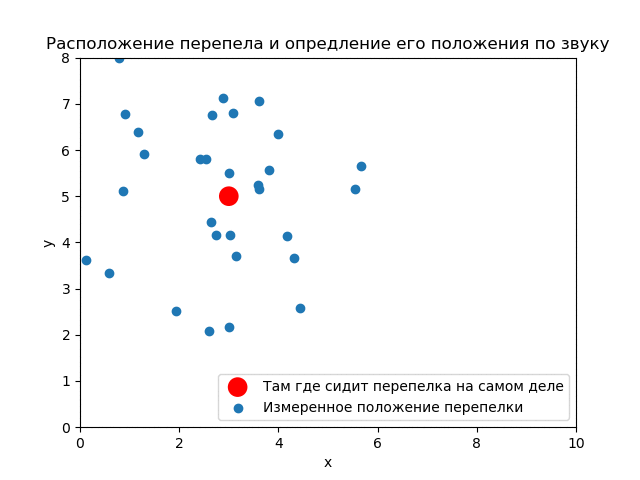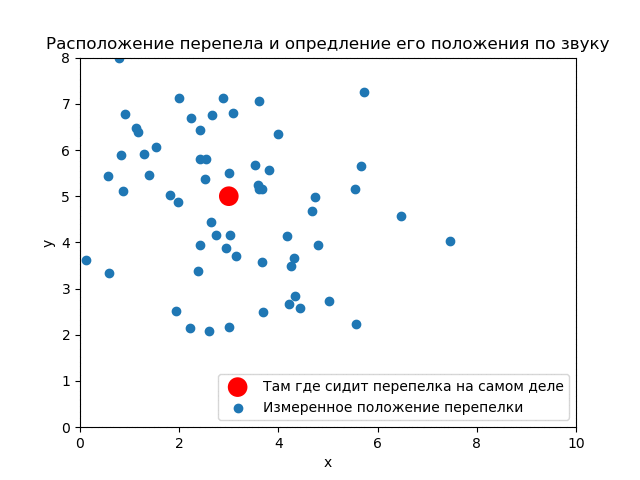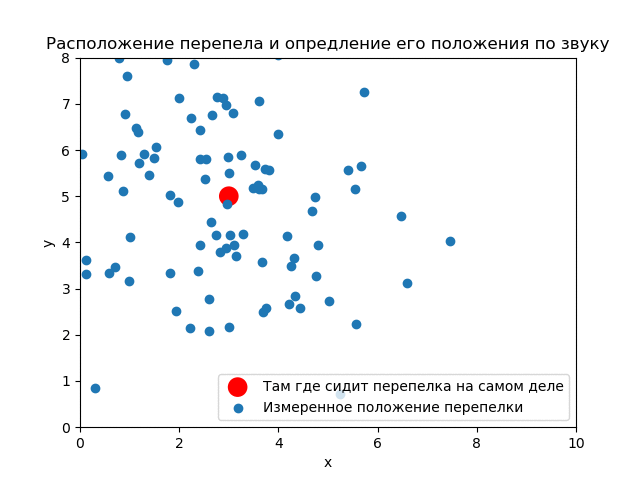
$f_{posterior}(X)$ — ;
$f_{prior}(X)$ — ;
$f_{mes}(X)$ — .
:

f_{m e s} (X) = \frac{1}{(2 π)^{2} d e t K} e^{\frac{1}{2} (Y - X)^{T} K^{- 1} (Y - X)},

$\begin{equation} f_{mes}(X) = \frac{1}{(2\pi)^2 detK} e^{ \frac {1}{2} (Y-X)^T K^{-1} (Y-X)}, \end{equation}$

$K$ — ;
$Y$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ .
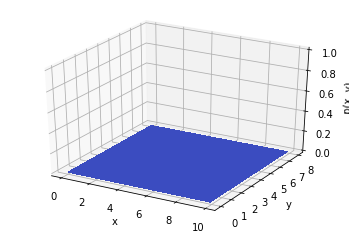
L'animation ci-dessous montre comment la distribution change d'une expérience à l'autre.

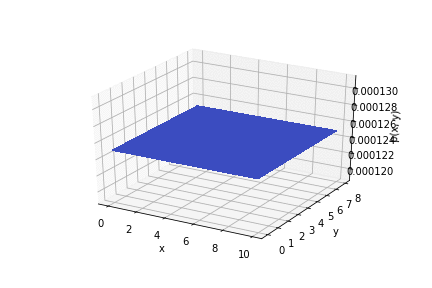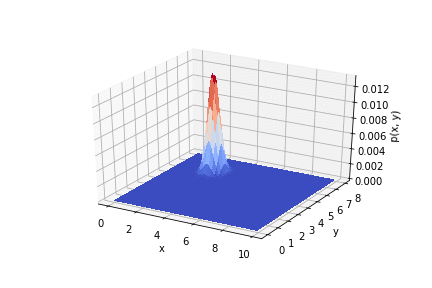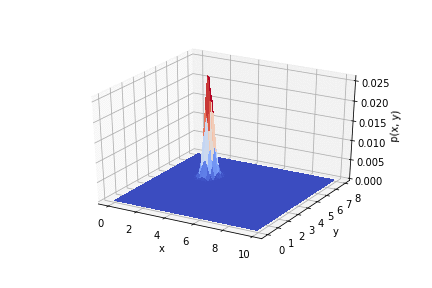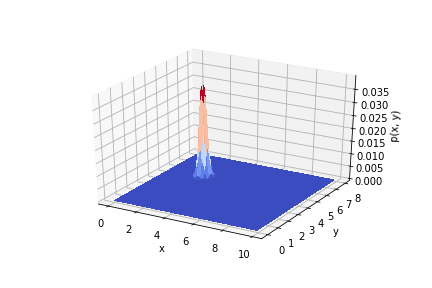
Code pour le lien .

Conclusion

Ainsi, on voit comment les résultats de l'expérience affectent la distribution a priori. Si vous utilisez correctement les mesures, vous pouvez obtenir une bonne précision.
Mais n’est-il pas plus facile de simplement trouver la moyenne de toutes les mesures et donc d’évaluer l’emplacement de la caille? Bien sûr. Cet exemple n'est qu'un bon exemple du théorème de Bayes pour les variables aléatoires continues. Le but de l'article est de trancher la théorie.

Arrêtez-vous au Dave Channel pendant ces semaines d'auto-isolement. Bon à tous.

Ninja Bayésien

Formulation du problème

Conclusion

More articles: