Bonne journée.
Pendant mon temps libre, j'ai fait quelques recherches.
En théorie des graphes, un algorithme de nombre de clics gourmand est connu. Loin de toujours, il donne le bon résultat. Sous la coupe se trouve une analyse des résultats de l'algorithme gourmand lorsqu'il est combiné avec une énumération partielle des ensembles de sommets sur les graphiques de l'ensemble de référence DIMACS.
La colonne «Mieux connu» du tableau 1 montre la taille des clics maximums actuellement connus des graphiques indiqués. La colonne «Gourmand» affiche les tailles de clic maximales trouvées par l'algorithme gourmand. L'algorithme gourmand ne donne la bonne réponse que dans 3 cas sur 35.
Remarque - dans le code de programme implémenté, l'algorithme gourmand sélectionne le sommet avec la valeur d'adjacence la plus élevée. Si plusieurs sommets similaires sont trouvés, le premier trouvé est sélectionné. Nous appellerons la procédure d'algorithme gourmand Greedy (A), où A est le numéro du tableau (matrice d'adjacence) auquel l'algorithme est appliqué. Indexez le tableau initial comme A0.
Tableau 1 - Les résultats de l'algorithme implémenté en Pascal.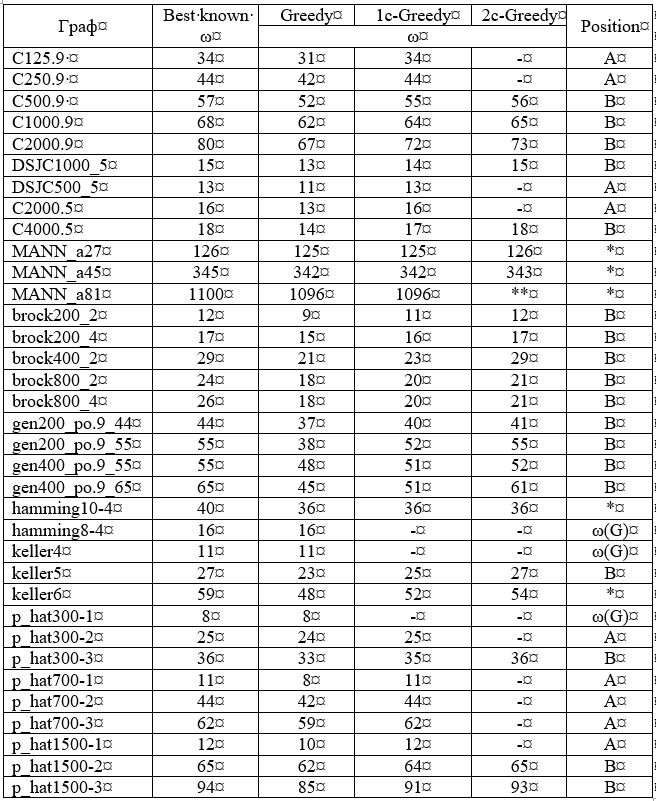 ** - non analysé en raison de la grande taille du graphique.
** - non analysé en raison de la grande taille du graphique., : N , . m, m – . DelNotAdj(m).
Greedy(m). ( ) «1c-Greedy». , , 8 35.
. , DelNotAdj(m). 0, m. mx. Greedy(mx). ( ) «2-Greedy».
3- (3c-Greedy) C500.9 C1000.9 ω(C500.9)=57, ω(C1000.9)=66.
.
Pascal Greedy(A) O(n2), n – . n , 2- – .. , ω(G) – () . .
, , ? 1 , .
( 1). O(n), – ω 1 ω(G) – , ωGR – , .
 1
1«Position» 1 . ꞷ(G) , . «» , .
«B» , 2- .
«*» , «», .. 2, 3 . ω. ωGRCFG.
, , , , . .. , , , 2- .
«» , :
- 0 «» . ωGR.
- «» m, m . m , . ωGR+1.
- «» mn, m- n- 0. mn , n- m- . ωGR+2.
- 3-, 4-,…, y- ωGR+3, ωGR+4,…, ωGR+y .
- 0 — ω(G).
. «» «B» :
, , ωGR. ωGR+1 ωGR, 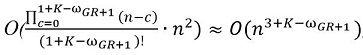 , K – .
, K – .
«*» :
«» ωGR, ωGR+1, ωGR+2,…, ω(G) . , , . , ωGR.
: ωGR, ωGR+1, ωGR+2,… , « » ( ωGRCDE 1).
:
1. «» ωGR+y,
ωGR+y-1, 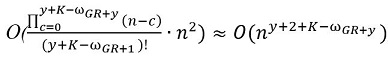 , K – .
, K – .
.
2. y- ωGR+y, , .. ωGR+y=ωGR+y-1, , ωGR+y ω(G) .
Si ce qui précède répète le travail de quelqu'un d'autre, je ne suis pas par dépit, je serai heureux de voir le lien. Je serai encore plus heureux si quelqu'un peut théoriquement prouver ou infirmer les hypothèses proposées.