Les paramètres et principes de fonctionnement de divers systèmes peuvent être reliés par un attribut sélectionné entre eux avec différents types de relations. Si, disons, nous nous intéressons à l'effet du prix d'un service sur sa demande, alors cette relation peut être décrite par une relation de type «influence», «fortement influence», «affecte faiblement», etc. Dans ce cas, des objets assez «discrets» pour la description peuvent ne pas suffire. Pour de nombreux problèmes appliqués à la théorie des automates, à la reconnaissance des formes, à la prise de décision, etc. il est logique de généraliser le concept de la relation entre les objets à un cas flou. De plus, le modèle, très probablement, décrira plus adéquatement le système, permettant une analyse qualitative des systèmes sans perte de seuil d'information, en lien avec l'émergence de nouveaux types de relations: similitude, similitude, dissimilarité, ...
Le concept de relations floues (connexions, associations, relations, relations sont synonymes), ainsi que le concept d'ensembles flous, fait référence aux fondements fondamentaux de toute la théorie des ensembles flous. En plus du fait qu'ils ont eux-mêmes appliqué une valeur, sur la base d'un certain nombre de concepts supplémentaires qui sont utilisés pour construire des modèles flous de systèmes plus complexes.
Relation floue
 (Désolé)
(Désolé)Définition
Comme dans le cas de l' ensemble flou (HM), la relation floue généralise le concept de la relation habituelle habituelle dans la théorie des ensembles (naïfs). Et de nombreux concepts présentés ci-dessous pour les relations seront similaires aux concepts correspondants pour NM.
Nous introduisons les concepts de relation floue et considérons ses propriétés.
Rapport flou 2-aire (binaire) sur l'ensemble universel , . :
n- n- .
, - ( , ..). . . , n- .
.
- ;
- ;
- ;
- , — , — . ( , . , , , xD)
.
Laissez sur le plateau relation floue définie «Beaucoup plus» (x >> y). Alors la matrice de cette relation et le graphe auront respectivement la forme:

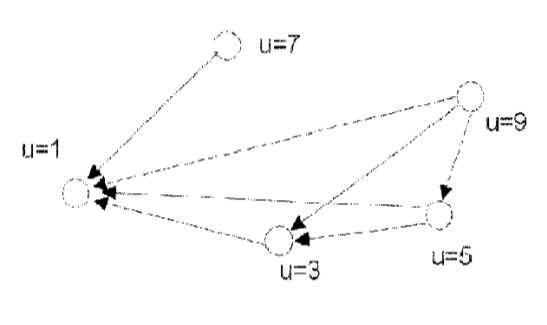
—
:
,
( ) :
:
:
, , — .
, :
, , 0.5 0.
, .
:
. L'ensemble de toutes les relations floues forme un réseau distributif par rapport aux opérations d'union et d'intersection; et de l'accomplissement des identités d'idempotence, de commutativité, d'associativité, d'absorption et de distributivité pour le réseau l'accomplissement de ces identités pour toutes les relations s'ensuit.Dans une logique basée sur la théorie des ensembles ordinaires, une déclaration comme «les nombres x et y sont très proches ou / et très différents» devrait être réduite à «les nombres x et y sont très proches ou très différents». Cependant, dans la théorie des ensembles flous, la première affirmation est tout à fait logique; elle exprime le fait que le «et» conjonctif est interprété pour de très petites valeurs de la fonction d'appartenance, lorsqu'il est impossible de dire à propos de x et y qu'ils sont très proches ou qu'ils sont très différents les uns des autres. Cet exemple illustre bien la flexibilité des énoncés inhérents à la logique réelle.
: ; : .
, . - . , . - . , .
( ) . .
. , . (Max-*)-. , 3 .
- max-min ( ): . .
- min-max ( ): .
- max-• ( ): .
Qu'il y ait deux relations sur le composé de deux éléments. Matrices de relations:
Alors les compositions de ces relations seront respectivement:
- ;
- ;
- .
. :
:;
: ;
: ;
flexx: ;
: ;
: ;
: ;
: .
… . .
2 NPC-, . , . NPC :
, , .
, , — .
, , :
« »
« »
« »
. : NPC ?
, :
def very(arr: List[set]):
return [(elem[0]**2, elem[1]) for elem in arr]
def no(arr: List[set]):
return [(1 - elem[0], elem[1]) for elem in arr]
def attitude(a: List[set], b: List[set], func = lambda x, y: min(x, y)):
return [[func(i[0], j[0]) for j in b] for i in a]
def attitude_unite(a: List[List], b: List[List]):
return [[max(a[i][j], b[i][j]) for j in range(len(a[i]))] for i in range(len(a))]
def composition(a: List[List], b: List[List]):
result = [[0 for j in range(len(b[0]))] for i in range(len(a))]
for x in range(len(a)):
for z in range(len(b[0])):
maximum = min(a[x][0], b[0][z])
for y in range(0, len(a[0])):
if maximum < min(a[x][y], b[y][z]):
maximum = min(a[x][y], b[y][z])
result[x][z] = maximum
return result
def index_plus(a: List[List]):
maximum = max([elem[1] for elem in a])
result = 0
for i in range(len(a)):
result += a[i][0] * (a[i][1] + maximum) / 2
return result
def ranking_index(a: List[List], b: List[List]):
return index_plus(a) - index_plus(b)
, — -. , , , index_plus ranking_index. . ( ; , ) :
— . . :
A = [(0.8, 3), (0.4, 15), (0.3, 30)]
B = [(0.1, 0.9), (0.5, 0.5), (0.8, 0.1)]
C = [(0.8, 0.9), (0.5, 0.5), (0.3, 0.2)]
— « ». 1 3 :
x = no(very(A))
x = [[elem[0] for elem in x]]
NPC K1R1. R1=A×B ∪ A¯×B¯:
AonB = attitude(A, B)
notAonnotB = attitude(no(A), no(B))
R1 = attitude_unite(AonB, notAonnotB)
y1, ( ) R1.
y1 = composition(x, R1)
print('y1 = ', y1)
:
notAonC = attitude(no(A), C)
AonnotC = attitude(A, no(C))
R2 = attitude_unite(notAonC, AonnotC)
y2 = composition(x, R2)
print('y2 = ', y2)
y1y2:
y1 = [(y1[0][i], B[i][1]) for i in range(len(y1[0]))]
y2 = [(y2[0][i], C[i][1]) for i in range(len(y2[0]))]
NPC:
print('index = ', ranking_index(y1, y2))
Une petite valeur négative indique que K2acceptent plus fidèlement les objets et sont plus susceptibles de compter la quête du joueur que K1.
Et c'est tout pour aujourd'hui.