🏇🏿 👨🏾‍🏭 🚌 Méthodes de Monte Carlo pour les chaînes de Markov (MCMC). introduction 👲🏾 🤳🏽 🙇🏿

Bonjour, Habr!

Nous vous rappelons que nous avons annoncé plus tôt le livre " Machine Learning Without Extra Words " - et maintenant il est déjà en vente . Malgré le fait que pour les débutants en MO, le livre puisse en effet devenir un ordinateur de bureau , certains sujets n'y étaient toujours pas abordés. Par conséquent, nous proposons à toutes les personnes intéressées une traduction d'un article de Simon Kerstens sur l'essence des algorithmes MCMC avec la mise en œuvre d'un tel algorithme en Python.

Les méthodes de Monte Carlo pour les chaînes de Markov (MCMC) sont une classe puissante de méthodes d'échantillonnage à partir de distributions de probabilités connues uniquement jusqu'à une certaine constante de normalisation (inconnue).
Cependant, avant de plonger dans le MCMC, voyons pourquoi vous pourriez même avoir besoin de faire une telle sélection. La réponse est: vous pouvez être intéressé soit par les échantillons eux-mêmes de l'échantillon (par exemple, pour déterminer des paramètres inconnus en utilisant la méthode de dérivation bayésienne), soit pour approximer les valeurs attendues des fonctions par rapport à la distribution de probabilité (par exemple, pour calculer les quantités thermodynamiques à partir de la distribution des états en physique statistique). Parfois, nous ne nous intéressons qu'au mode de distribution des probabilités. Dans ce cas, nous l'obtenons par la méthode d'optimisation numérique, il n'est donc pas nécessaire de faire une sélection complète.

Il s'avère que l'échantillonnage de toutes les distributions de probabilités, à l'exception des plus primitives, est une tâche difficile. La méthode de transformation inverse est une technique élémentaire d'échantillonnage à partir de distributions de probabilités, qui nécessite cependant l'utilisation d'une fonction de distribution cumulative, et pour l'utiliser, à son tour, vous devez connaître la constante de normalisation, qui est généralement inconnue. En principe, une constante de normalisation peut être obtenue par intégration numérique, mais cette méthode devient rapidement impraticable avec une augmentation du nombre de dimensions. Échantillonnage par déviationIl ne nécessite pas une distribution normalisée, mais pour le mettre en œuvre efficacement, il faut beaucoup de choses sur la distribution qui nous intéresse. De plus, cette méthode souffre gravement de la malédiction des dimensions - cela signifie que son efficacité diminue rapidement avec une augmentation du nombre de variables. C'est pourquoi vous devez organiser intelligemment la réception d'échantillons représentatifs de votre distribution - sans avoir besoin de connaître la constante de normalisation.

Les algorithmes MCMC sont une classe de méthodes conçues spécifiquement pour cela. Ils reviennent à l' article historique de Metropolis et d'autres ; Metropolis a développé le premier algorithme MCMC nommé d' après luiet conçu pour calculer l'état d'équilibre d'un système bidimensionnel de sphères dures. En fait, les chercheurs recherchaient une méthode universelle qui nous permettrait de calculer les valeurs attendues en physique statistique.
Cet article couvrira les bases de l'échantillonnage MCMC.

CHAÎNES DE MARKOV

Maintenant que nous comprenons pourquoi nous devons échantillonner, passons au cœur de MCMC: les chaînes de Markov. Qu'est-ce qu'une chaîne Markov? Sans entrer dans les détails techniques, nous pouvons dire qu'une chaîne de Markov est une séquence aléatoire d'états dans un certain espace d'état, où la probabilité de choisir un certain état dépend uniquement de l'état actuel de la chaîne, mais pas de son histoire passée: cette chaîne est dépourvue de mémoire. Dans certaines conditions, une chaîne de Markov a une distribution stationnaire unique d'états, vers laquelle elle converge, surmontant un certain nombre d'états. Après un tel nombre d'états dans une chaîne de Markov, une distribution invariante est obtenue.

Pour échantillonner à partir d'une distribution,

l'algorithme MCMC crée et simule une chaîne de Markov dont la distribution stationnaire est

; cela signifie qu'après la période initiale de «graine», les états d'une telle chaîne de Markov sont distribués selon le principe

. Par conséquent, nous n'aurons qu'à enregistrer l'état afin d'en obtenir des échantillons

.

À des fins éducatives, considérons à la fois un espace d'état discret et un «temps» discret. La quantité clé caractérisant une chaîne de Markov est un opérateur de transition

indiquant la probabilité d'être dans un état

à un moment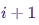

, à condition que la chaîne soit dans un état

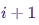au moment i.
Maintenant juste pour le plaisir (et comme démonstration) tissons rapidement une chaîne Markov avec une distribution stationnaire unique. Commençons par quelques importations et paramètres pour les graphiques:

%matplotlib notebook
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 6]
np.random.seed(42)

La chaîne de Markov fera le tour de l'espace d'état discret formé par trois conditions météorologiques:

state_space = ("sunny", "cloudy", "rainy")

Dans un espace d'états discret, l'opérateur de transition n'est qu'une matrice. Dans notre cas, les colonnes et les lignes correspondent à un temps ensoleillé, nuageux et pluvieux. Choisissons des valeurs relativement raisonnables pour les probabilités de toutes les transitions:

transition_matrix = np.array(((0.6, 0.3, 0.1),
                              (0.3, 0.4, 0.3),
                              (0.2, 0.3, 0.5)))

Les lignes indiquent les états dans lesquels le circuit peut actuellement être situé, et les colonnes indiquent les états dans lesquels le circuit peut aller. Si nous prenons le pas de «temps» de la chaîne de Markov dans une heure, alors, à condition qu'il soit ensoleillé maintenant, il y a 60% de chances que le temps ensoleillé continue pendant l'heure suivante. Il y a également 30% de chances que le temps soit nuageux au cours de la prochaine heure et 10% de chances qu'il pleuve immédiatement après un temps ensoleillé. Cela signifie également que les valeurs de chaque ligne totalisent un.
Conduisons un peu notre chaîne Markov:

n_steps = 20000
states = [0]
for i in range(n_steps):
    states.append(np.random.choice((0, 1, 2), p=transition_matrix[states[-1]]))
states = np.array(states)

Nous pouvons observer comment la chaîne de Markov converge vers une distribution stationnaire, calculant la probabilité empirique de chacun des états en fonction de la longueur de la chaîne:

def despine(ax, spines=('top', 'left', 'right')):
    for spine in spines:
        ax.spines[spine].set_visible(False)

fig, ax = plt.subplots()
width = 1000
offsets = range(1, n_steps, 5)
for i, label in enumerate(state_space):
    ax.plot(offsets, [np.sum(states[:offset] == i) / offset 
            for offset in offsets], label=label)
ax.set_xlabel("number of steps")
ax.set_ylabel("likelihood")
ax.legend(frameon=False)
despine(ax, ('top', 'right'))
plt.show()

HONNEUR DE TOUS LES MCMC: ALGORITHME DE MÉTROPOLE-HASTINGS

Bien sûr, tout cela est très intéressant, mais revenons au processus d'échantillonnage d'une distribution de probabilité arbitraire

. Elle peut être soit discrète, auquel cas nous continuerons à parler de la matrice de transition

, soit continue, auquel cas ce

sera un noyau de transition. Nous parlerons ci-après de distributions continues, mais tous les concepts que nous considérons ici sont également applicables à des cas discrets.

Si nous pouvions concevoir le noyau de transition de manière à ce que l'état suivant soit déjà déduit

, cela pourrait être limité, car notre chaîne de Markov ... serait directement échantillonnée

. Malheureusement, pour y parvenir, nous devons pouvoir échantillonner

ce que nous ne pouvons pas faire - sinon vous ne liriez pas cela, non?

La solution consiste à diviser le noyau de transition

en deux parties: l'étape de proposition et l'étape d'acceptation / rejet. Une distribution auxiliaire apparaît à l'étape d'échantillonnage

parmi lesquels les prochains états possibles de la chaîne sont sélectionnés. Non seulement nous pouvons faire une sélection à partir de cette distribution, mais nous pouvons choisir arbitrairement la distribution elle-même. Cependant, lors de la conception, il faut s'efforcer de parvenir à une configuration dans laquelle les échantillons prélevés dans cette distribution seraient en corrélation minimale avec l'état actuel et auraient en même temps de bonnes chances de passer par la phase de réception. L'étape de réception / rejet ci-dessus est la deuxième partie du noyau de transition; à ce stade, les erreurs contenues dans les états d'essai sélectionnés sont corrigées

. Ici, la probabilité de réception réussie est calculée

et un échantillon est prélevé

avec une probabilité telle que l'état suivant dans la chaîne. Obtenir le prochain état

puis effectué comme suit: d'abord, l'état d'essai

est tiré de

. Ensuite, il est considéré comme le prochain état avec probabilité

ou rejeté avec probabilité

, et dans ce dernier cas, l'état actuel est copié et utilisé comme prochain. Par
conséquent, nous avons

condition suffisante pour la chaîne de Markov a

une distribution stationnaire est la suivante: Le noyau de transition doit présenter un équilibre détaillé ou écrire dans la littérature physique, la réversibilité microscopique :

.

Cela signifie que la probabilité d'être dans un état

et de passer de là à

doit être égal à la probabilité du processus inverse, c'est-à-dire pouvoir

et entrer dans un état

. Les noyaux de transition de la plupart des algorithmes MCMC remplissent cette condition.
Pour que le noyau de transition en deux parties obéisse à l'équilibre détaillé, il est nécessaire de choisir correctement

, c'est-à-dire de s'assurer qu'il vous permet de corriger les asymétries dans le flux de probabilité de / vers

. Algorithme de Metropolis-Hastings utilise critère de recevabilité Metropolis:

.

Et ici, la magie commence:

nous ne connaissons qu'une constante, mais cela n'a pas d'importance, car cette constante inconnue annule l'expression de

! C'est cette propriété paccpacc qui assure le fonctionnement d'algorithmes basés sur l'algorithme Metropolis-Hastings sur des distributions non normalisées. Des distributions auxiliaires symétriques c sont souvent utilisées

, auquel cas l'algorithme Metropolis-Hastings est réduit à l'algorithme Metropolis original (moins général) développé en 1953. Dans l'algorithme d'origine

.

Dans ce cas, le noyau de transition complet de Metropolis-Hastings peut s'écrire

.

NOUS METTONS EN ŒUVRE L'ALGORITHME METROPOLIS-HASTINGS À PYTHON

Eh bien, maintenant que nous avons compris comment fonctionne l'algorithme Metropolis-Hastings, passons à sa mise en œuvre. Premièrement, nous établissons la probabilité logarithmique de la distribution à partir de laquelle nous allons faire une sélection - sans constantes de normalisation; on suppose que nous ne les connaissons pas. Ensuite, nous travaillons avec la distribution normale standard:

def log_prob(x):
     return -0.5 * np.sum(x ** 2)

Ensuite, nous choisissons une distribution auxiliaire symétrique. En général, les performances de l'algorithme Metropolis-Hastings peuvent être améliorées si vous incluez des informations déjà connues de la distribution à partir de laquelle vous souhaitez effectuer une sélection dans la distribution auxiliaire. Une approche simplifiée ressemble à ceci: nous prenons l'état actuel xet sélectionnons un échantillon à partir de

, c'est-à-dire, définissons une certaine taille de pas Δet allons à gauche ou à droite de notre état actuel par pas plus de

def proposal(x, stepsize):
    return np.random.uniform(low=x - 0.5 * stepsize, 
                             high=x + 0.5 * stepsize, 
                             size=x.shape)

Enfin, nous calculons la probabilité d'acceptation de la proposition:

def p_acc_MH(x_new, x_old, log_prob):
    return min(1, np.exp(log_prob(x_new) - log_prob(x_old)))

Maintenant, nous mettons tout cela ensemble dans une mise en œuvre vraiment brève de la phase d'échantillonnage pour l'algorithme Metropolis-Hastings:

def sample_MH(x_old, log_prob, stepsize):
    x_new = proposal(x_old, stepsize)
    #   ,     :
    #       [0,1]  
    #     
    accept = np.random.random() < p_acc(x_new, x_old, log_prob)
    if accept:
        return accept, x_new
    else:
        return accept, x_old

En plus du prochain état de la chaîne de Markov, x_newou x_old, nous renvoyons également des informations pour savoir si l'étape MCMC a été adoptée. Cela nous permettra de suivre la dynamique de la collecte d'échantillons. En conclusion de cette implémentation, nous écrivons une fonction qui appellera itérativement sample_MHet donc construira une chaîne de Markov:

def build_MH_chain(init, stepsize, n_total, log_prob):

    n_accepted = 0
    chain = [init]

    for _ in range(n_total):
        accept, state = sample_MH(chain[-1], log_prob, stepsize)
        chain.append(state)
        n_accepted += accept
    
    acceptance_rate = n_accepted / float(n_total)
    
    return chain, acceptance_rate

TESTER NOTRE ALGORITHME METROPOLIS-HASTINGS ET RECHERCHER SON COMPORTEMENT

Probablement, maintenant, vous avez hâte de voir tout cela en action. Nous le ferons, nous prendrons des décisions éclairées sur les arguments stepsizeet n_total:

chain, acceptance_rate = build_MH_chain(np.array([2.0]), 3.0, 10000, log_prob)
chain = [state for state, in chain]
print("Acceptance rate: {:.3f}".format(acceptance_rate))
last_states = ", ".join("{:.5f}".format(state) 
                        for state in chain[-10:])
print("Last ten states of chain: " + last_states)
Acceptance rate: 0.722
Last ten states of chain: -0.84962, -0.84962, -0.84962, -0.08692, 0.92728, -0.46215, 0.08655, -0.33841, -0.33841, -0.33841

Les choses sont bonnes. Alors ça a marché? Nous avons réussi à prélever des échantillons dans environ 71% des cas et nous avons une chaîne d'états. Les premiers États dans lesquels la chaîne n'a pas encore convergé vers sa distribution stationnaire doivent être écartés. Vérifions si les conditions que nous avons choisies ont bien une distribution normale:

def plot_samples(chain, log_prob, ax, orientation='vertical', normalize=True,
                 xlims=(-5, 5), legend=True):
    from scipy.integrate import quad
    
    ax.hist(chain, bins=50, density=True, label="MCMC samples",
           orientation=orientation)
    #     PDF
    if normalize:
        Z, _ = quad(lambda x: np.exp(log_prob(x)), -np.inf, np.inf)
    else:
        Z = 1.0
    xses = np.linspace(xlims[0], xlims[1], 1000)
    yses = [np.exp(log_prob(x)) / Z for x in xses]
    if orientation == 'horizontal':
        (yses, xses) = (xses, yses)
    ax.plot(xses, yses, label="true distribution")
    if legend:
        ax.legend(frameon=False)
    
fig, ax = plt.subplots()
plot_samples(chain[500:], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()

Cela semble très bien!

Qu'en est-il des paramètres stepsizeet n_total? Nous discutons d'abord de la taille de l'étape: elle détermine dans quelle mesure l'état d'essai peut être retiré de l'état actuel du circuit. Par conséquent, il s'agit d'un paramètre de distribution auxiliaire qqui contrôle la taille des pas aléatoires de la chaîne de Markov. Si la taille du pas est trop grande, les états d'essai se retrouvent souvent dans la queue de la distribution, où les valeurs de probabilité sont faibles. Le mécanisme d'échantillonnage de Metropolis-Hastings ignore la plupart de ces étapes, ce qui entraîne une réduction des taux de réception et un ralentissement significatif de la convergence. Voir par vous-même:

def sample_and_display(init_state, stepsize, n_total, n_burnin, log_prob):
    chain, acceptance_rate = build_MH_chain(init_state, stepsize, n_total, log_prob)
    print("Acceptance rate: {:.3f}".format(acceptance_rate))
    fig, ax = plt.subplots()
    plot_samples([state for state, in chain[n_burnin:]], log_prob, ax)
    despine(ax)
    ax.set_yticks(())
    plt.show()
    
sample_and_display(np.array([2.0]), 30, 10000, 500, log_prob)
Acceptance rate: 0.116

Pas très cool, non? Il semble maintenant qu'il est préférable de définir une taille de pas minuscule. Il s'avère que ce n'est pas non plus une décision intelligente, car la chaîne de Markov étudiera la distribution de probabilité très lentement et ne convergera donc pas aussi rapidement qu'avec une taille de pas bien choisie:

sample_and_display(np.array([2.0]), 0.1, 10000, 500, log_prob)
Acceptance rate: 0.992

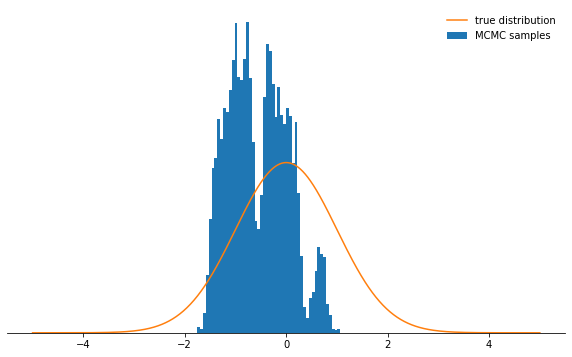Quelle que soit la façon dont vous choisissez le paramètre de taille de pas, la chaîne de Markov converge finalement vers une distribution stationnaire. Mais cela peut prendre beaucoup de temps. Le temps pendant lequel nous simulerons la chaîne de Markov est n_totaldéterminé par le paramètre - il détermine simplement le nombre d'états de la chaîne de Markov (et, par conséquent, les échantillons sélectionnés) que nous aurons éventuellement. Si la chaîne converge lentement, alors elle doit être augmentée n_totalpour que la chaîne de Markov ait le temps «d'oublier» l'état initial. Par conséquent, nous allons laisser la taille de l'étape minuscule et augmenter le nombre d'échantillons en augmentant le paramètre n_total:

sample_and_display(np.array([2.0]), 0.1, 500000, 25000, log_prob)
Acceptance rate: 0.990

Nous progressons plus lentement vers l'objectif ...

CONCLUSIONS

Compte tenu de tout ce qui précède, j'espère que vous avez maintenant compris intuitivement l'essence de l'algorithme Metropolis-Hastings, ses paramètres, et comprenez pourquoi il s'agit d'un outil extrêmement utile pour sélectionner des distributions de probabilités non standard que vous pouvez rencontrer dans la pratique.

Je vous recommande fortement d'expérimenter avec le code donné ici.- pour vous habituer au comportement de l'algorithme dans diverses circonstances et le comprendre plus profondément. Essayez la distribution auxiliaire asymétrique! Que se passera-t-il si vous ne définissez pas correctement les critères d'acceptation? Que se passe-t-il si vous essayez d'échantillonner à partir d'une distribution bimodale? Pouvez-vous trouver un moyen d'ajuster automatiquement la taille du pas? Quels sont les pièges ici? Répondez à ces questions vous-même!

Méthodes de Monte Carlo pour les chaînes de Markov (MCMC). introduction

More articles: