Loi de Faraday ou comment un aimant se coince dans un tuyau en cuivre

Image tirée du site Web de Popular Mechanics.

Beaucoup ont vu l'expérience avec un aimant permanent qui semble coincé à l'intérieur d'un tube de cuivre à paroi épaisse. Dans cet article, nous comprendrons la physique du processus.
Tout d'abord, nous écrivons la formule du champ magnétique de l'aimant permanent et calculons le flux magnétique qui traverse la section transversale du tuyau, puis faisons bouger l'aimant et découvrons le courant électrique induit qui se produit dans le métal, quelle est la puissance électrique dissipée, écrivons et résolvons l'équation du mouvement de l'aimant permanent.

Et si vous avez lu cet endroit et n'avez pas eu peur, bienvenue à kat - alors ce sera plus intéressant!

Je réfléchis moi-même depuis longtemps pour bien comprendre ce problème. Et récemment, une conversation avec un collègue de travail a commencé. On a demandé à son enfant de faire une démonstration scientifique à l'école, pour laquelle papa a obtenu un morceau de tuyau en cuivre et un aimant néodyme-fer-bore. L'enfant a compris, fait une démonstration de son expérience devant la classe, a donné des explications, mais ni la classe ni l'enseignant n'ont été particulièrement impressionnés. Lors d'un concours d'expériences scientifiques, un volcan (!) À partir de soude et d'acide citrique a gagné =) Mon collègue et moi avons jeté un coup d'œil rapide et réalisé que c'était clair, qu'il faisait noir. Et dans la littérature, peu de choses ont été écrites sur ce sujet. Cette conversation m'a motivé à essayer de traverser la jungle. Dans cet article, j'écris ce que j'ai fait.

Description de l'expérience

Commençons par regarder une vidéo démontrant l'expérience. Avant de plonger dans la théorie, il sera utile de présenter une image de ce qui se passe en général. Sur Internet, cette expérience a été expliquée et démontrée à plusieurs reprises sur vidéo. Mais je dois également le décrire ici, afin que plus tard, nous sachions clairement de quoi nous repoussons.

L'expérimentateur place un aimant permanent sous la forme d'une petite boule dans un tuyau en cuivre, qu'il tient verticalement. Contrairement aux attentes, la balle ne tombe pas à travers le tuyau avec une accélération de la gravité, mais se déplace à l'intérieur du tuyau beaucoup plus lentement.

Ainsi, par expérience, nous observons comment un aimant permanent se déplace à l'intérieur d'un tuyau en cuivre creux à une vitesse constante. Nous fixons un point arbitraire dans le corps du tube de cuivre et dessinons mentalement une coupe transversale. Un flux magnétique généré par un aimant permanent traverse cette section du tuyau en cuivre. En raison du fait que l'aimant se déplace le long du tuyau, une variableflux magnétique, augmentant ou diminuant selon que l'aimant s'approche ou s'éloigne du point où nous avons conduit mentalement la section. Selon les équations de Maxwell, un flux magnétique alternatif génère un champ électrique vortex, en général, dans tout l'espace. Cependant, seulement là où il y a un conducteur, ce champ électrique met en mouvement des charges libres situées dans le conducteur - un courant électrique circulaire apparaît, qui crée déjà son propre champ magnétique et interagit avec le champ magnétique d'un aimant permanent en mouvement. En termes simples, un courant électrique circulaire crée un champ magnétique du même signe qu'un aimant permanent, et une certaine force dissipative agit sur l'aimant, et en particulier la force de frottement. Le lecteur peut à juste titre poser une question:"Friction de quoi et de quoi?" La friction se produit entre le champ magnétique du dipôle et le conducteur. Oui, ce frottement n'est pas mécanique. Au contraire, les corps ne se touchent pas. Eh bien laissez! Il y a encore des frictions!

En général, en mots, tout semble plus ou moins complexe, mais cela peut-il être décrit dans le langage des mathématiques? Commençons ...

Description mathématique

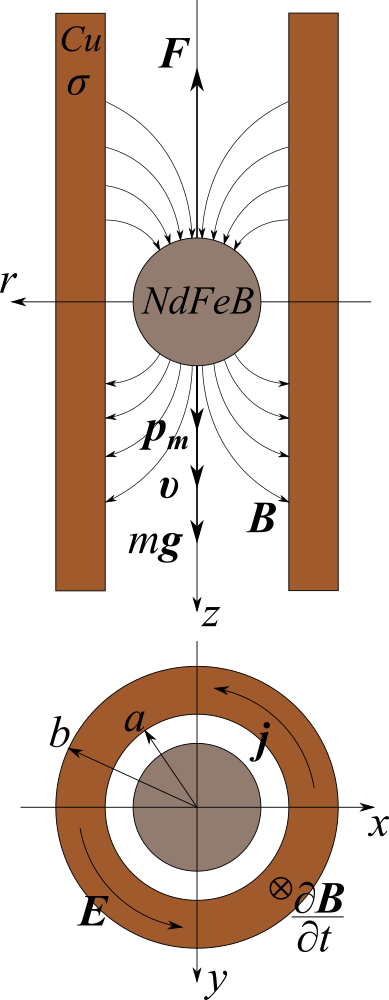Tout d'abord, nous avons besoin d'un modèle mathématique d'un aimant permanent. À mon avis, il sera commode d'imaginer un aimant permanent comme un dipôle magnétique.

$$

$$\vec{B}=\frac{\mu_0}{4\pi}\left(\frac{3(\vec{p}_m\cdot\vec{r})\vec{r}}{r^5}-\frac{\vec{p}_m}{r^3}\right)$$

La notation est acceptée ici. $$$\vec{r}=(r,z)$ Est le vecteur de rayon du centre du dipôle au point d'observation, $$$\vec{p}_m$Est le vecteur du moment dipolaire.

Ensuite, nous devons écrire$$$z$- une composante du vecteur d'induction magnétique pour calculer le flux magnétique capté dans la section transversale du métal du tuyau en cuivre. Nous écrivons$$$z$-composante du champ magnétique ici

$$

$$B_z(r,z) = \frac{\mu_0\,p_m}{4\pi}\frac{2z^2 - r^2}{\left(r^2 + z^2\right)^\frac{5}{2}}$$

Maintenant, nous écrivons l'expression du flux magnétique à travers la zone couverte par un cercle de rayon $$$r$ à distance $$$z$ du dipôle.

$$

$$\Phi(r,z) = \int_0^{2\pi}\int_0^r B_z(r',z)\,r'\,dr'\,d\varphi = 2\pi\int_0^r \frac{\mu_0\,p_m}{4\pi}\frac{2z^2 - r'^2}{\left(r'^2 + z^2\right)^\frac{5}{2}}\,r'\,dr'$$

Vous ne le croirez pas, mais cette intégrale est prise. Je ne vais pas ennuyer. La réponse est très belle

$$

$$\Phi(r,z) = \frac{\mu_0\,p_m}{2}\frac{r^2}{\left(r^2 + z^2\right)^\frac{3}{2}}$$

En raison du fait que le dipôle se déplace le long de l'axe $$$z$ avec vitesse $$$v$, vous devez également effectuer une recherche standard $$$\Phi(r, z)\rightarrow \Phi(r, z - v t)$
Il semble qu'il est temps d'appeler à l'aide l'une des grandes équations de Maxwell, à savoir l'équation même qui décrit la loi de Faraday :

Changement du flux magnétique traversant une surface ouverte $$$S$prise avec le signe opposé est proportionnelle à la circulation du champ électrique en boucle fermée $$$L$qui est la limite de la surface $$$S$

$$

$$\oint_L \vec{E}\,dl = -\frac{\partial}{\partial t}\int_S \vec{B}\,d\vec{s}$$

Ou, la même chose

$$

$$2\pi r E_\varphi = -\frac{\partial}{\partial t}\Phi(r,z - v t)$$

Ici, nous avons utilisé la symétrie axiale du problème par rapport à l'axe $$$z$, et a également pris en compte que le champ électrique induit n'a que la composante azimutale $$$\vec{E} = E_\varphi \vec{e}_\varphi$.
De là, on peut trouver la composante azimutale du champ électrique induit par l'aimant.

$$

$$E_\varphi(r,z) = -\frac{1}{2\pi r}\frac{\partial}{\partial t}\Phi(r, z - v t)=-\frac{3\mu_0\,p_m}{4\pi}\frac{rv(z-v t)}{\left(r^2 + (z-v t)^2\right)^\frac{5}{2}}$$

Maintenant que nous avons une expression pour le champ électrique, nous pouvons rappeler le tuyau. Comme le montre la figure ci-dessus, le rayon intérieur du tuyau est$$$a$et l'extérieur - $$$b$. Le matériau du tuyau est en cuivre. Pour le moment, nous n'aurons besoin que de la conductivité électrique du cuivre. Nous désignons la conductivité par$$$\sigma$.
Un champ électrique à l'intérieur d'un conducteur provoque un courant électrique. Par conséquent, nous pouvons écrire la loi d'Ohm sous forme différentielle

$$

$$\vec{j} = \sigma \vec{E}$$

Le courant électrique, à son tour, provoque des pertes ohmiques à l'intérieur du conducteur. En d'autres termes, l'énergie est dissipée à l'intérieur du conducteur et prend la forme de chaleur, à proprement parler, dans notre cas, dans tout le volume du conducteur.
La densité volumique volumique des pertes ohmiques est par définition égale à

$$

$$w = \vec{j}\cdot\vec{E} = \sigma E^2$$

D'un autre côté, lorsque l'aimant se déplace de haut en bas, l'énergie potentielle de l'aimant dans le champ gravitationnel de la Terre diminue, cependant, la vitesse de mouvement reste constante, c'est-à-dire qu'elle n'augmente pas , comme c'est le cas avec la chute libre. Cela ne signifie qu'une chose: l'énergie potentielle de l'aimant est dissipée à l'intérieur du conducteur. Et du point de vue des forces agissant sur l'aimant, la force de frottement agit sur lui, ce qui le ralentit et dissipe l'énergie potentielle de l'aimant en chaleur.
Nous écrivons maintenant le bilan de puissance dans le problème: le taux de diminution de l'énergie potentielle est égal à la puissance des pertes ohmiques dans le conducteur.

$$

$$\frac{dE_p}{dt} = P$$

$$

$$-mg\dot{z} = \int_V w\,dV$$

$$

$$mgv = \int_{-\infty}^{\infty}\int_0^{2\pi}\int_a^b \sigma E^2\,r\,dr\,d\varphi\,dz$$

Il convient de noter ici que l'énergie potentielle dans les coordonnées indiquées dans la figure ci-dessus sera égale à $$$E_p = - mgz$, et pour trouver la puissance totale des pertes ohmiques, il faut intégrer $$$w$sur tout le volume du conducteur. Nous considérons que la longueur du tuyau est infinie. Ce n'est pas si loin de la vérité, étant donné que dans l'expérience de la vidéo, le diamètre de l'aimant est beaucoup plus petit que la longueur du tuyau.

La dernière triple intégrale semble très compliquée. Et c'est comme ça! Mais, premièrement, l'intégration azimutale$$$\varphi$ peut être remplacé simplement en multipliant par $$$2\pi$en raison de la symétrie axiale du problème. Deuxièmement, l'ordre d'intégration dans cette intégrale particulière peut être modifié et d'abord intégré sur$$$z$puis après $$$r$. Troisièmement, lors de l'intégration sur$$$z$ sur des limites infinies, nous pouvons écarter en toute sécurité le terme $$$-vt$. L'intégrale restante est prise par la machine.

$$

$$\int_{-\infty}^\infty \frac{z^2\,dz}{\left(r^2 + z^2\right)^5} = \frac{5\pi}{128r^7}$$

Le résultat est une réponse pour la pleine puissance des pertes ohmiques

$$

$$P = \frac{15}{1024}\,\mu_0^2\,p_m^2\,\sigma\left(\frac{1}{a^3} - \frac{1}{b^3}\right)v^2 = k\,v^2$$

Ici, après le deuxième signe égal, nous avons désigné le coefficient de frottement

$$

$$k = \frac{15}{1024}\,\mu_0^2\,p_m^2\,\sigma\left(\frac{1}{a^3} - \frac{1}{b^3}\right)$$

Notez que le coefficient de frottement $$$k$ ne dépend que de la magnétisation de l'aimant $$$p_m$, propriétés des matériaux conducteurs $$$\sigma$ et dimensions géométriques du tuyau $$$a$ et $$$b$- c'est-à-dire qu'elle dépend uniquement des paramètres de l'aimant et du tuyau et ne dépend pas, par exemple, de la vitesse ou du temps. C'est un bon signe pour nous et un petit crédit pour les formules trouvées! À partir de là, il devient clair pourquoi un tuyau en cuivre a été choisi pour démontrer l'expérience, et non, disons, un tuyau en acier. Le frottement dépend linéairement de la conductivité$$$\sigma$, et la conductivité de l'acier est inférieure d'un ordre de grandeur.



Peut maintenant enregistrer

$$

$$mgv=kv^2\\mg = kv$$

Et soudain (!), Devant nous est la troisième loi de Newton! La force de l'action est égale à la force de la réaction. Nous pouvons trouver la vitesse constante de l'aimant

$$

$$v_s = \frac{mg}{k}$$

Équation du mouvement

C'était le tour de l'équation du mouvement. En utilisant la deuxième loi de Newton, il sera écrit très simplement

$$

$$ma=mg - kv\\ m\ddot{z} + k\dot{z} = mg$$

Résoudre l'équation pour $$$z(t)$inintéressant, car bon, juste les coordonnées changent à vitesse constante. Il est beaucoup plus utile de savoir à quelle vitesse la chute se stabilise, ce qui équivaut au taux de chute en régime permanent. En général, vous devez résoudre cette équation de vitesse

$$

$$\dot{v} + \frac{k}{m} v = g$$

Et la solution sera

$$

$$v(t) = v_0\,e^{-\alpha t} + v_s\left(1 - e^{-\alpha t}\right)$$

Ici $$$\alpha = k/m$- coefficient d'atténuation. Le temps caractéristique pour atteindre le mode de chute stable est$$$\tau = \alpha^{-1}$. Vitesse de démarrage -$$$v_0$, vitesse constante - $$$v_s$.

En général, c'est l'équation d'un parachutiste. C'est probablement pourquoi l'article de Popular Mechanics est intitulé «Magnetic Parachute».

Expérience numérique

Et maintenant, il y aura quelque chose pour lequel tout cela a été conçu. Vous avez apporté une théorie ici, vous savez. De quoi est-elle capable? Tout à coup, c'est comme une ombre sur la clôture en bois? Ou cela ne fonctionne pas du tout ...

Vous devez d'abord gérer la géométrie du problème. La vidéo du MIT est donc américaine. Je vais essayer de deviner la taille de leur installation de démonstration en pouces (ils aiment aussi tout mesurer en pouces). La taille de l'aimant est similaire à$$$d = 1/2$pouces de diamètre. C'est l'un de ceux qui sont en vente. Ensuite, la masse d'un tel aimant sera d'environ$$$m = 8$ d. La longueur du tuyau en cuivre est similaire à $$$l = 12$ pouces (1 pi), et les diamètres intérieur et extérieur du tuyau sont très probablement $$$2a = 3/4$ pouces $$$2b = 3/2$pouces.

Avec la géométrie, en quelque sorte trié. Maintenant propriétés physiques. Conductivité du cuivre$$$59.5\times 10^6$S / m

Plus tôt, il était écrit ici que je ne pouvais pas lier la magnétisation résiduelle d'un aimant au néodyme à son moment magnétique équivalent. Mais il y avait de bonnes personnes dans les commentaires. UtilisateurDenishwla source a suggéré (voir le paragraphe 5 dans la liste des références) où vous pouvez lire, a aidé à faire les calculs nécessaires, et même les a vérifiés sur le simulateur FEMM.


Calcul du champ magnétique d'une balle à partir de NdFeB sur le simulateur FEMM. Image fournie par l'utilisateurDenishw

Alors, ce qui a été découvert. L'aimant NdFeB appartient à la classe des paramagnets, car sous l'influence d'un champ externe, le champ interne est amplifié. De plus, l'alliage NdFeB est capable de maintenir le champ interne après la fin du champ externe. Ce fait classe le NdFeB comme un ferromagnet. Si nous désignons l'induction du champ interne d'un aimant par$$$B$et le champ magnétique externe $$$H$puis l'égalité

$$

$$B = \mu \mu_0 H = (1 + \chi)\mu_0 H = \mu_0(H + I)$$

Ici $$$\chi$ - la susceptibilité magnétique de la substance, et $$$I$Est le vecteur de magnétisation de la substance.

Lorsqu'un aimant est fabriqué dans une usine, il est magnétisé par un champ extérieur.$$$H$puis le champ externe est désactivé, et l'aimant conserve une certaine aimantation résiduelle $$$B_r$. On sait que pour les aimants en néodyme, la magnétisation rémanente est d'environ$$$B_r = 1\,..\,1.3$ Maintenant, si vous excluez le champ externe $$$H$ de l'équation précédente, nous obtenons

$$

$$B_r = \mu_0I$$

Où trouve-t-on le moment magnétique par unité de volume de matière $$$I$ comme

$$

$$I = \frac{B_r}{\mu_0}$$

Pour trouver le moment magnétique de l'aimant dans son ensemble, vous devez multiplier $$$I$ par volume de balle $$$V$

$$

$$p_m=IV=I\cdot\frac{4}{3}\pi\left(\frac{d}{2}\right)^3$$

Pour la magnétisation résiduelle $$$B_r = 1$ T est obtenu $$$p_m = 0.853$Am².
Voici un graphique$$$z$- composantes du champ magnétique en fonction de la coordonnée radiale dans notre problème à une distance de la moitié du diamètre de la balle.


$$$z$-composante d'un champ magnétique près de la surface d'un aimant permanent

Une fois qu'il était possible de mesurer avec un appareil. Les champs directement sur la surface de ces aimants sont généralement inférieurs à la magnétisation résiduelle et s'élèvent à plusieurs milliers de Gauss. Ce que j'ai mesuré pour un aimant rectangulaire était d'environ 4 500 Gs. Par conséquent, nous avons un résultat très réaliste sur le tracé du champ magnétique.

Nous allons maintenant utiliser la solution de l'équation du mouvement pour tracer la vitesse de l'aimant. Pour tous les paramètres sélectionnés ci-dessus, le coefficient de frottement est égal à$$$k = 1.015$ N / (m / s), vitesse constante - $$$v_s = 7.77$cm / s - environ 3 pouces par seconde! Dans la vidéo, la balle passe à travers un tuyau de 12 pouces en environ 4 secondes.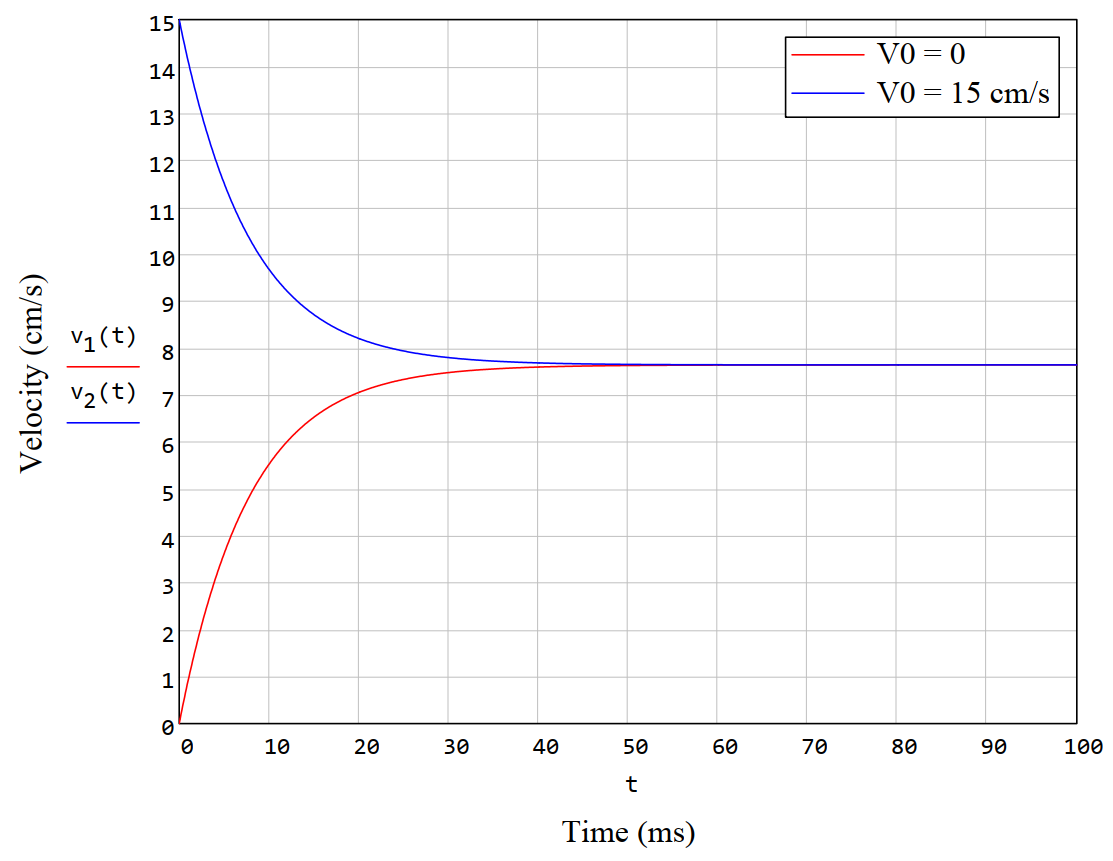


Graphique pour résoudre l'équation de mouvement d'un aimant dans un tuyau en cuivre


Et nous continuons. La dissipation de puissance est d'environ$$$P \approx 6$ mW, et le temps caractéristique pour atteindre l'état d'équilibre est $$$\tau \approx 8$SP Voici les graphiques.$$$v(t)$ pour deux vitesses initiales différentes: zéro, et $$$v_0 = 15$cm / s.

Et en plus, l'utilisateurvashu1a fait remarquer à juste titre qu'il serait bon de connaître le courant induit dans un tuyau en cuivre. Eh bien, et c'est possible. Intégrer

$$

$$J = \int_{0}^{\infty}\int_a^b \sigma E(r,z)\,dr\, dz = \frac{\sigma\, v\,\mu_0\, p_m}{4\pi}\left(\frac{1}{a} - \frac{1}{b}\right)$$

Intégrer par $$$z$il est nécessaire selon des limites semi-infinies, puisque dans l'autre moitié du tuyau le courant circule dans le sens opposé. J'ai la réponse$$$J = 20$R. Honnêtement, je ne m'attendais pas à recevoir un si gros courant. Chez l'utilisateurvashu1il s'est avéré 50 A, ce qui, apparemment, n'est pas loin non plus de la réalité. je pensevashu1J'ai calculé la somme des courants dans l'ensemble du tuyau, ce qui, pour des raisons de puissance, est également raisonnable.

Voici une telle étude. J'espère que c'était intéressant. Laissez vos commentaires. Je vais essayer de répondre à tout le monde. Si vous avez aimé l'article, soutenez l'auteur comme ou plus dans le karma. Merci d'avoir lu.

Littérature

1. Jackson, J. Électrodynamique classique: Per. de l'anglais Monde, 1965.
2. Landau, L.D., et Lifshitz, E.M. (1941). Théorie des champs. Moscou; Leningrad: Maison d'édition d'État de littérature technique et théorique.
3. Sivukhin, D. V. «Cours général de physique. Volume 3. Électricité. " Moscou, maison d'édition "Science", l'édition principale de la littérature physique et mathématique (1977).
4. Yavorsky, B. M. et A. A. Detlaf. "Handbook of Physics." (1990).
5. Kirichenko N.A. Électricité et magnétisme. Didacticiel. - M.: MIPT, 2011 .-- 420 p.