Négociation d'arbitrage (algorithme Bellman-Ford)

La négociation en bourse est généralement associée à des risques. Cela est absolument vrai pour la plupart des stratégies de trading. Le succès du commerce dans ces cas est déterminé uniquement par la capacité d'évaluer correctement les risques et de les gérer. Mais toutes les stratégies de trading ne le sont pas. Il existe des stratégies sans risque, qui incluent notamment l'arbitrage. Cet article explique ce qu'est l'arbitrage et comment l'implémenter en utilisant un algorithme de graphe classique tel que l'algorithme de Bellman-Ford.

Qu'est-ce que l'arbitrage?

L'arbitrage consiste en quelques transactions logiquement liées visant à profiter de la différence de prix pour le même actif ou des actifs connexes en même temps sur différents marchés (arbitrage spatial), ou sur le même marché à différents moments dans le temps (arbitrage temporaire) .

À titre d'exemple simple, considérons l'arbitrage spatial. À New York et à Londres, des accords peuvent être conclus pour acheter des dollars pour des euros et des euros pour des dollars. A New York, cela peut se faire au tarif de 4 dollars pour 3 euros, et à Londres - au tarif de 5 dollars pour 3 euros. Cette différence de taux ouvre la possibilité d'un arbitrage spatial.



Avec 4 dollars, à New York, vous pouvez acheter 3 euros. Après cela, à Londres, achetez pour ces 3 euros 5 dollars. Comme vous pouvez le voir, une séquence de transactions aussi simple apporte 1 dollar de profit pour 4 dollars investis. Par conséquent, s'il y a initialement 4 millions de dollars, le profit sera déjà de un million.

Lorsque les taux de change (nous ne considérons pas l'écart) pour la même paire de devises diffèrent, la séquence des transactions requises pour mettre en œuvre la stratégie d'arbitrage est très simple. Si le taux de change pour une paire de devises est fixe, mais que plusieurs paires de devises sont négociées en parallèle, l'arbitrage est également possible, mais la séquence des transactions sera déjà non triviale. Par exemple, vous pouvez acheter 4 euros pour 5 dollars, 3 livres pour 4 euros, puis 6 dollars pour 3 livres. Le profit d'une telle séquence de transactions sera de 1 $ pour chaque 5 dollars investis.



Des centaines de paires de devises peuvent être échangées en bourse et les taux de change changent constamment. Il est déjà impossible de comprendre quelle séquence de transactions apportera des bénéfices sans une solution algorithmique.

Transition vers le problème algorithmique

Imaginez des transactions de change potentielles sous une forme algorithmique, à savoir sous la forme d'un graphique. Les sommets de ce graphique représentent les devises et les bords sont des transactions potentielles. La longueur de la nervure correspond au taux de change auquel la transaction peut être conclue.


La question suivante est de savoir comment trouver une séquence de transactions dans une telle colonne qui apportera des bénéfices. Évidemment, puisqu'au début de la séquence et à la fin il doit s'agir de la même monnaie, la séquence doit correspondre au cycle du graphe donné. Ensuite, vous devez déterminer comment le taux de change entre les deux devises est calculé, si elles ne sont pas échangées directement, mais via une certaine troisième devise (ou un nombre arbitraire d'opérations intermédiaires). Tout ici est également assez simple. Un tel taux de change sera calculé comme le produit des taux de change des transactions intermédiaires. Une séquence de transactions rentable devient si ce produit prend une valeur inférieure à un. En d'autres termes, si une unité monétaire peut être achetée moins qu'une unité de la même monnaie.


Les algorithmes de graphe classiques sont mal adaptés pour travailler avec des produits de longueurs d'arête. Ces algorithmes visent principalement à trouver un chemin défini comme la somme de ces longueurs. Cependant, pour contourner cette limitation, il existe un moyen mathématique de passer d'un produit à une somme. De cette façon, c'est le logarithme. Si le produit apparaît sous le logarithme, alors un tel logarithme peut être converti en la somme des logarithmes. Sur le côté droit de cette équation, le nombre souhaité est inférieur à un, ce qui signifie que le logarithme de ce nombre doit être inférieur à zéro.




Une telle astuce mathématique simple vous permet de passer de la recherche d'un cycle dont le produit des longueurs d'arêtes est inférieur à un à la recherche d'un cycle dont la somme des longueurs d'arêtes est inférieure à zéro. Une telle tâche semble déjà plus résoluble par les algorithmes de graphes classiques, et plus précisément l'algorithme de Bellman-Ford.

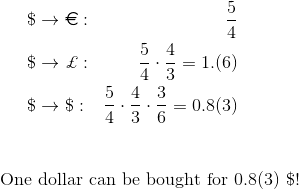
Bellman - Algorithme Ford

L'algorithme Bellman-Ford est généralement utilisé pour trouver la distance d'un sommet donné à tous les autres sommets d'un graphique, mais sa modification permet de trouver des cycles de longueur négative.

L'opération de base de cet algorithme est la relaxation des bords. L'essence de cette opération est la suivante. Supposons qu'il y ait un bord$$$a \rightarrow b$, ainsi que les valeurs préliminaires des distances aux pics précédemment calculées sont connues $$$a$et $$$b$. Pour effectuer une relaxation des bords, il est nécessaire de calculer la distance par rapport au sommet.$$$b$si le chemin passait par le haut $$$a$et côtes $$$a \rightarrow b$. Cette distance est calculée comme la somme de la distance jusqu'au sommet.$$$a$ et longueurs de côtes $$$a \rightarrow b$. De plus, si cette distance est inférieure à la distance préliminaire actuelle$$$a$alors c'est la distance à $$$a$Correspond et prend une nouvelle valeur, juste calculée.

Le reste de l'algorithme est également simple. Nécessaire$$$N$ fois ($$$N$Est le nombre de sommets du graphique) contourner la liste des arêtes, en appliquant une opération de relaxation pour chaque tour. La complexité de l'algorithme est obtenue$$$N*M$ (Où $$$N$- le nombre de sommets, et $$$M$- nombre de côtes). Pour un graphique sans cycles négatifs, une relaxation supplémentaire des bords n'entraînera pas de changement de la distance aux sommets. En même temps, pour un graphique contenant un cycle négatif, la relaxation réduira la distance aux sommets et après$$$N$détours. Cette propriété peut être utilisée pour trouver le cycle souhaité.

La petite implémentation suivante de l'algorithme décrit ci-dessus sur Kotlin devrait aider ceux qui sont plus familiers avec le tri du code.

fun findNegativeCycle(nodes: Int, edges: Array<Edge>, source: Int): List<Int>? {
    // Initialize distances and prev arrays. All distances but the distance to
    // the source node are infinite, distance to the source node is zero.
    val distances = DoubleArray(nodes) { if (it == source) 0.0 else INFINITY }
    val prev = IntArray(nodes) { -1 }

    // Relax all edges N times where N is the number of nodes.
    repeat(nodes) {
        edges.forEach { it.relax(distances, prev) }
    }

    // Try to relax at least one more edge. If it's possible memorize the node,
    // otherwise return from the method.
    val firstRelaxedEdge = edges.firstOrNull { it.relax(distances, prev) }
    var node = firstRelaxedEdge?.to ?: return null

    // Step back N times where N is the number of nodes. As a result, the node will
    // be in the loop for sure.
    repeat(nodes) {
        node = prev[node]
    }

    // Recover the loop by the node that is inside it and prev links.
    val lastNode = node
    return buildList {
        do {
            add(node)
            node = prev[node]
        } while (node != lastNode)

        reverse()
    }
}

// Edge DTO with implemented relaxation operation.
data class Edge(val from: Int, val to: Int, val length: Double) {

    fun relax(distances: DoubleArray, prev: IntArray): Boolean {
        if (distances[from] + length >= distances[to]) {
            return false
        }

        distances[to] = distances[from] + length
        prev[to] = from
        return true
    }
}

Examinons un exemple avec un petit graphique, qui comprend un cycle de longueur négative. Pour que l'algorithme fonctionne, il est nécessaire que chaque sommet maintienne la distance connue actuelle à celui-ci, ainsi qu'un lien vers son sommet précédent. La référence au sommet précédent dans ce cas est déterminée par la relaxation réussie de la côte. Si l'opération de relaxation a réussi et que la distance au sommet a été mise à jour, le lien vers le sommet précédent de ce sommet est également mis à jour et prend la valeur du sommet source du bord donné.

Donc, vous devez d'abord initialiser les sommets en définissant la distance à tous les sommets sauf l'infini égal initial. Pour le sommet initial, une distance de zéro est définie.


Le premier tour de toutes les côtes suit et leur relaxation est effectuée. Presque toute la relaxation ne donne aucun résultat, sauf la relaxation des côtes$$$a \rightarrow b$. La relaxation de cette côte vous permet de mettre à jour la distance à$$$b$.


Ceci est suivi par le deuxième tour de tous les bords du graphique et la relaxation correspondante. Cette fois, le résultat est une relaxation des côtes.$$$b \rightarrow c$, et $$$b \rightarrow d$. Les distances aux sommets sont mises à jour.$$$c$ et $$$d$. Il est à noter ici que le résultat dépend de l'ordre dans lequel les bords sont traversés.


Au troisième tour de côtes, il est possible de détendre avec succès déjà trois côtes, à savoir les côtes $$$\rightarrow d$, $$$d \rightarrow e$, $$$d \rightarrow b$. Dans ce cas, lorsque les côtes sont détendues$$$\rightarrow d$ et $$$d \rightarrow b$distances déjà enregistrées $$$d$et $$$b$, ainsi que les liens correspondants vers les sommets précédents.


Au quatrième tour, les opérations de relaxation des côtes sont terminées avec succès. $$$b \rightarrow c$et $$$b \rightarrow a$. Dans ce cas, les valeurs déjà enregistrées des distances aux pics sont à nouveau mises à jour.$$$a$ et $$$c$, ainsi que les liens correspondants vers les sommets précédents.


Le cinquième tour est le dernier. Les côtes se détendent pendant cette promenade$$$\rightarrow d$, $$$d \rightarrow b$, $$$d \rightarrow e$. Ici, vous pouvez voir que la présence d'un cycle de longueur négative apporte déjà certains ajustements aux valeurs des distances aux pics.


Après cette tournée, si le graphique ne contenait pas de cycle de longueur négative, l'algorithme serait terminé, car la relaxation de n'importe quel bord n'aurait apporté aucun changement. Cependant, pour ce graphique, du fait de la présence d'un cycle de longueur négative, on peut encore trouver une arête dont la relaxation mettra à jour la distance à l'un des sommets.


On retrouve un bord dont la relaxation met à jour la distance jusqu'au sommet. Cela confirme la présence d'un cycle de longueur négative. Vous devez maintenant trouver ce cycle lui-même. Il est important que le sommet, dont la distance est maintenant mise à jour, puisse être à la fois à l'intérieur et à l'extérieur du cycle. Dans l'exemple, c'est le haut$$$e$et elle est hors cycle. Ensuite, vous devez vous référer aux liens vers les sommets précédents, qui ont été soigneusement mis à jour à toutes les étapes de l'algorithme. Pour être assuré d'entrer dans le cycle, vous devez prendre du recul$$$N$pics en utilisant ces liens.

Dans cet exemple, les transitions seront les suivantes:$$$e \rightarrow d \rightarrow c \rightarrow b \rightarrow d \rightarrow c$. Donc le sommet est situé$$$c$, qui est garanti de se situer dans un cycle de longueur négative.


De plus, une question de technologie. Pour retourner le cycle souhaité, vous devez réitérer en utilisant les liens vers les sommets précédents jusqu'à ce que le sommet se rencontre à nouveau$$$c$. Cela signifie que le cycle est terminé. Il ne reste plus qu'à inverser l'ordre, puisque l'itération a été inversée lors des itérations sur les liens vers les sommets précédents.

L'algorithme ci-dessus suppose la présence d'un sommet initial à partir duquel les distances sont calculées. La présence d'un tel sommet n'est pas nécessaire pour que l'algorithme fonctionne, mais il a été introduit dans une plus large mesure pour correspondre à l'algorithme Bellman-Ford d'origine. Si le sujet d'intérêt est un cycle de longueur négative, alors nous pouvons supposer que tous les sommets d'un graphe donné sont initiaux. En d'autres termes, la distance à tous les sommets est initialement nulle.

Conclusion

L'utilisation de l'algorithme Bellman-Ford dans le problème de la négociation d'arbitrage est un excellent exemple de la façon dont les algorithmes classiques peuvent résoudre de vrais problèmes commerciaux, en particulier dans le domaine financier. Complexité asymptotique de l'algorithme, égale à$$$N^3$pour un graphe entièrement connecté, il peut s'avérer assez volumineux. Il faut vraiment s'en souvenir. Cependant, dans de nombreux cas, comme l'échange de devises, cette complexité ne crée aucun problème en raison du nombre relativement faible de nœuds dans le graphique.