🙃 🍨 👩‍🍳 Visualisation des lignes de tension et des mouvements des charges électrostatiques, simulation du mouvement planétaire du système solaire 👸🏻 👩🏾‍✈️ 🚭

Bonjour, aujourd'hui, je veux vous offrir une aide visuelle pour modéliser certains processus physiques et montrer comment obtenir de belles images et animations. Attention beaucoup de photos.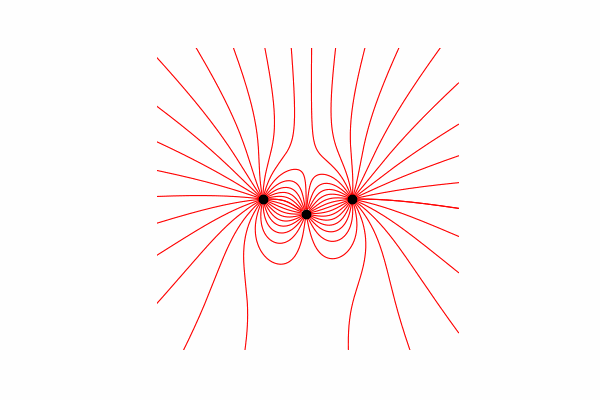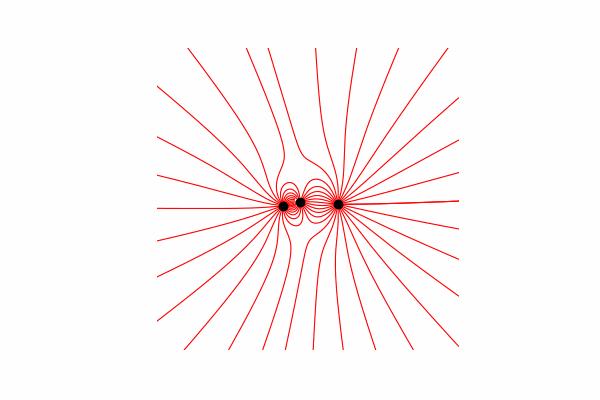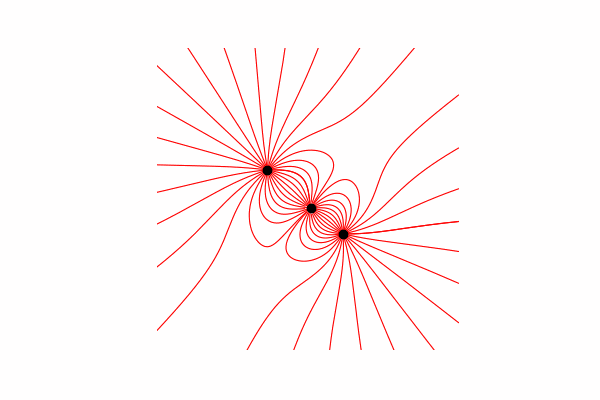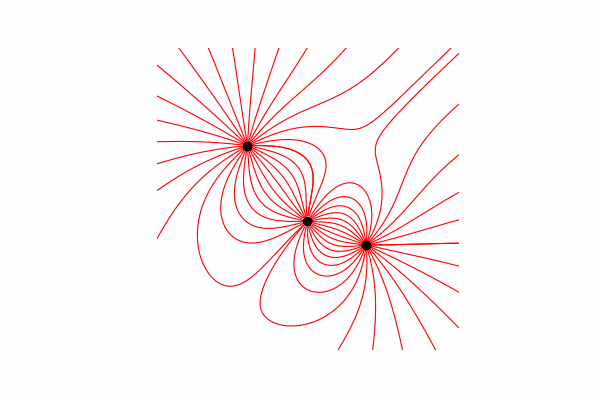

Tout le code se trouve dans google colab .

Théorie

Tout d'abord, nous avons besoin d'un petit minimum théorique sur ce sujet. Commençons par comprendre ce que sont les lignes de tension et comment les compter. En fait, ces lignes sont la fusion de nombreux vecteurs de tension, qui peuvent être calculés comme suit: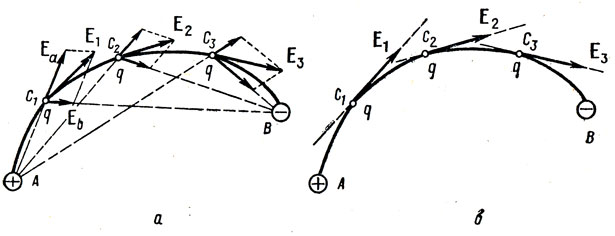

E = \frac{k * | q |}{r^{2}}

$E=\frac{k*|q|}{r^2}$ .

Méthode de calcul E

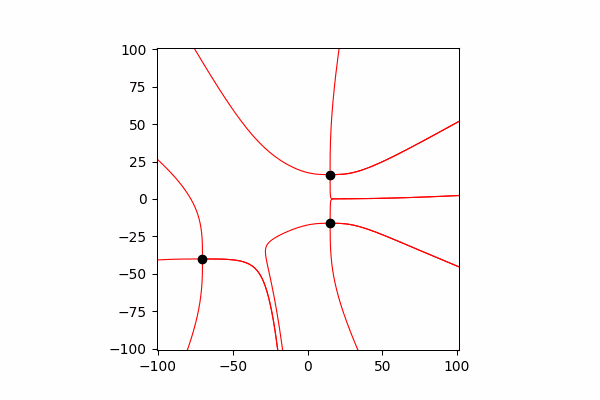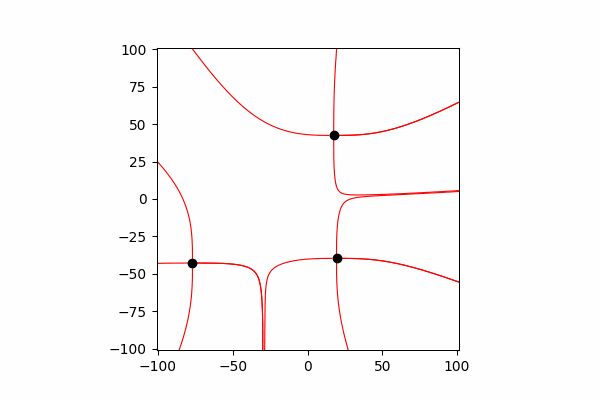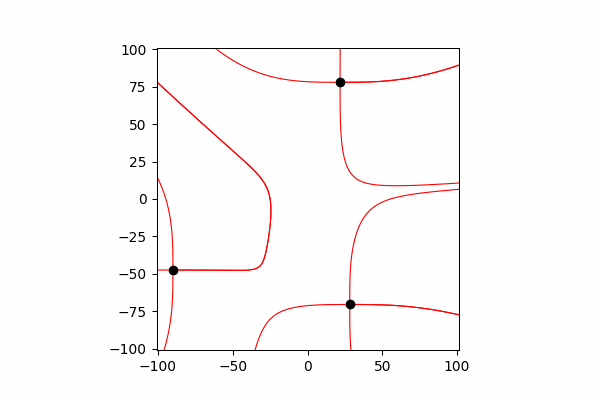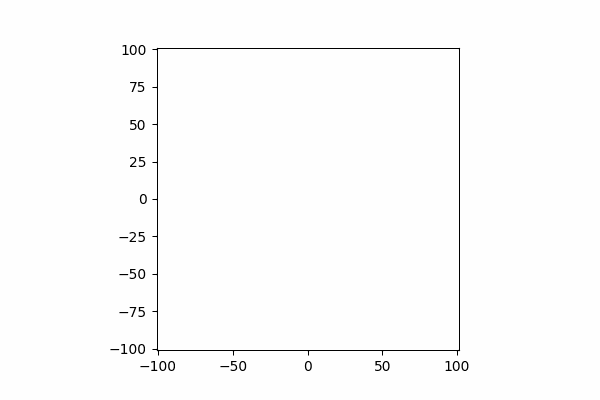
J'ai calculé le vecteur de tension à travers la similitude des triangles, obtenant ainsi des projections sur les axes x et y dx et dy, respectivement.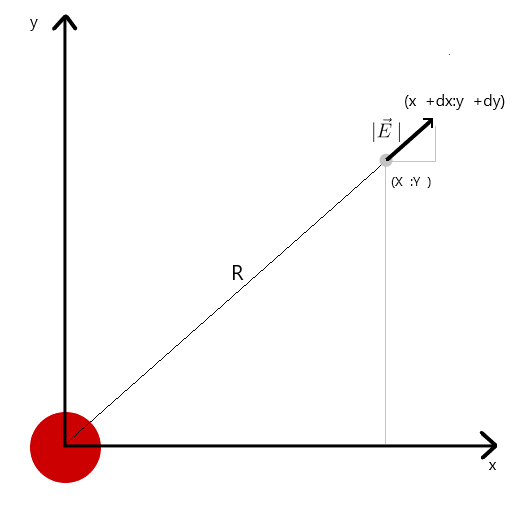

De la similitude, il s'ensuit que le rayon du vecteur de la charge au point dans l'espace r et la longueur du vecteur d'intensité E est égal au rapport des projections de ces vecteurs (respectivement x1 et dx)

\frac{R}{E} = \frac{x}{d x} = \frac{y}{d y}

$\frac{R}{E}=\frac{x}{dx}=\frac{y}{dy}$ . Formule du vecteur résultant

\vec{E} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{E}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{E}}_{i} |}{R_{i}} \end{matrix})

$\vec{E}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{E}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{E}_i|}{R_i} \end{array}\right) \qquad$
avec cette connaissance, nous obtenons le premier résultat.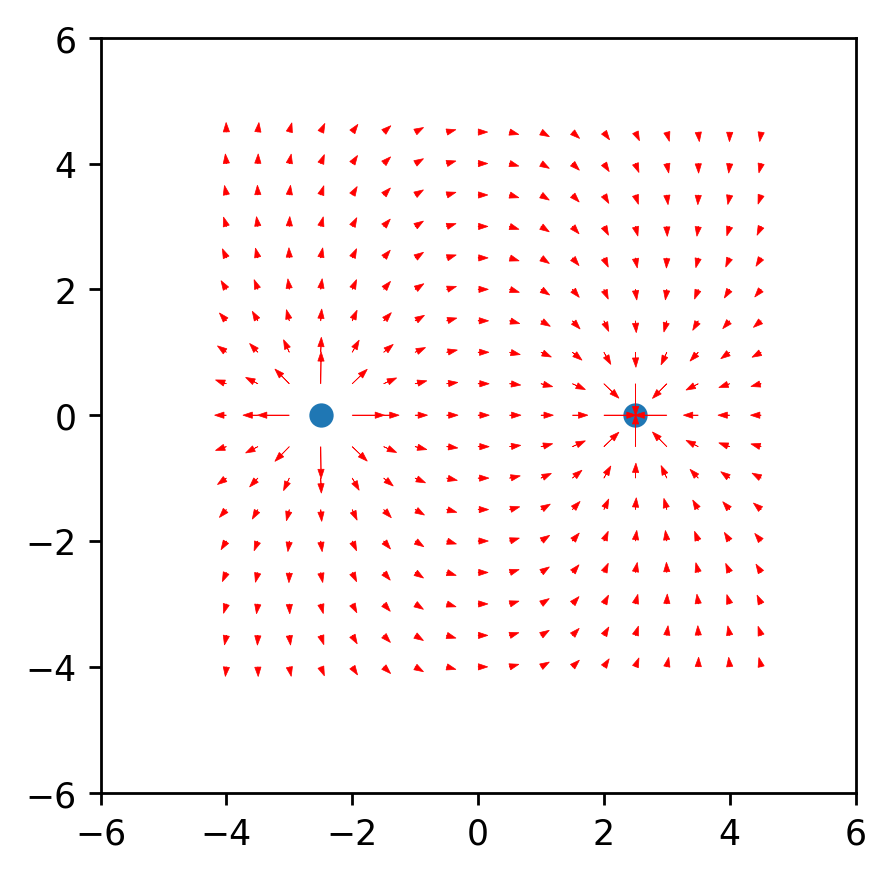

Fonction de calcul de projection

def E(q_prop, xs, ys, nq): #q_prop=[[xq1, yq1, q1, mq1, vxq1, vyq1], [xq2, yq2, q2, mq2, vxq2, vyq2] ... ] 
    l=1
    k=9*10**9
    Ex=0
    Ey=0
    c=0
    for c in range(len(q_prop)):#                
        q=q_prop[c]
        r=((xs-q[0])**2+(ys-q[1])**2)**0.5
        dEv=(k*q[2])/r**2
        dEx=(xs-q[0])*(dEv/r)*l
        dEy=(ys-q[1])*(dEv/r)*l

        Ex+=dEx
        Ey+=dEy
    return Ex, Ey

Méthode de construction de ligne

Vous devez d'abord décider du point de départ et d'arrivée de la ligne et du document. Le début est des points sur un cercle avec un rayon r autour de la charge, et les points finaux ne sont pas plus de r en dehors des charges.

code pour les points de départ

theta = np.linspace(0, 2*np.pi, n)
mask=q_prop[ q_prop[:,2]>0 ]#    
for cq in range(len(mask)):
    qmask=mask[cq]
    xr = r_q*np.cos(theta)+qmask[0]# -    
    yr = r_q*np.sin(theta)+qmask[1]#

Il vaut donc la peine de dire que les lignes sont construites uniquement à partir de charges positives.

Et enfin, la construction des lignes. Pour ce faire, nous construisons la ligne du vecteur de tension à partir du point de départ, mettons à jour le point de départ à la fin de la ligne construite et répétons jusqu'à ce que les conditions de fin mentionnées ci-dessus soient atteintes.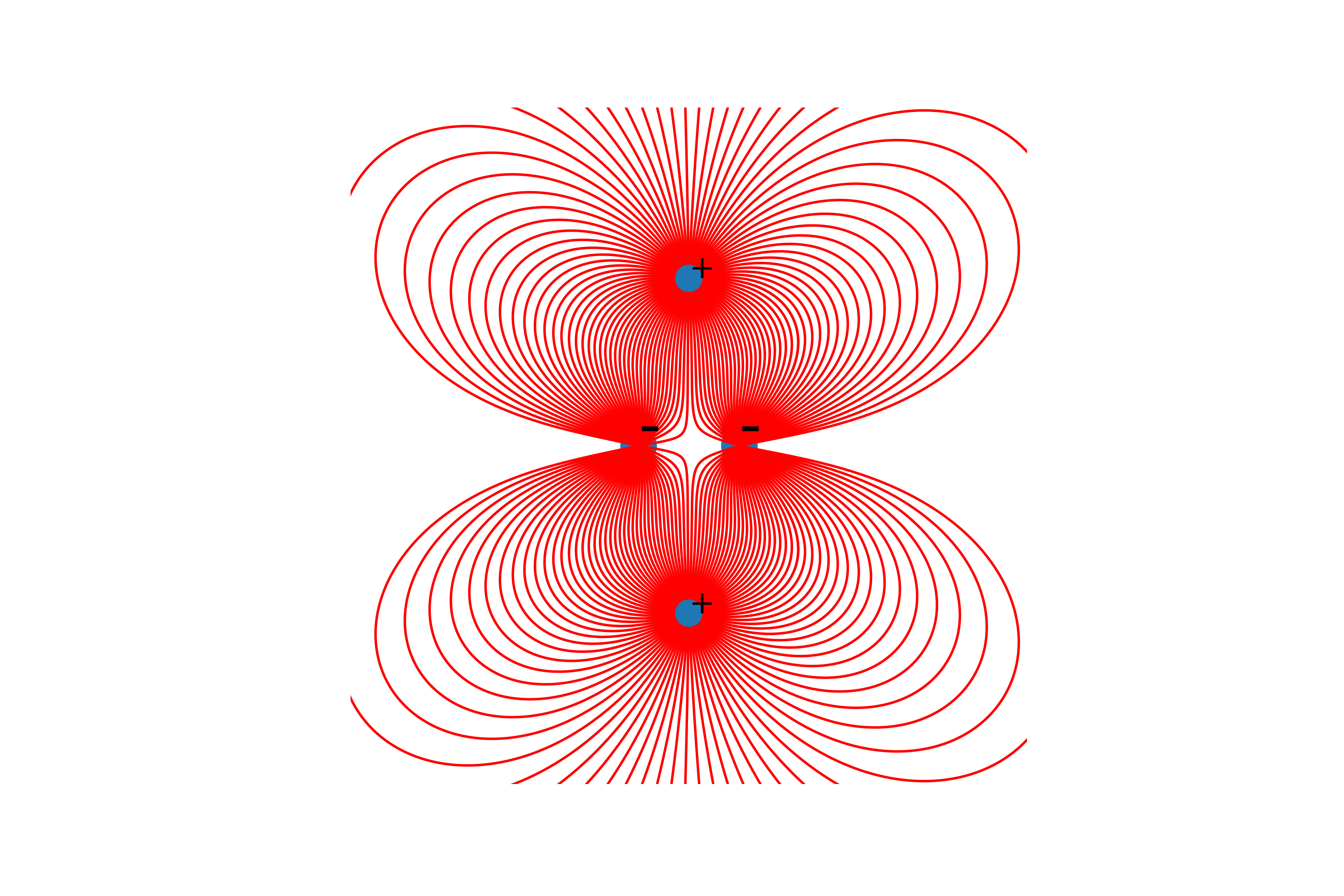

fonction de calcul des coordonnées de ligne

def Draw(size, q_prop,r_q, n):
  
  linen=np.empty((np.count_nonzero(q_prop[:,2]>0),n, 2000000), dtype=np.float64)
  linen[:] = np.nan
  theta = np.linspace(0, 2*np.pi, n)
  mask=q_prop[ q_prop[:,2]>0 ][ q_prop[q_prop[:,2]>0][:,3]==1 ]
  for cq in range(len(mask)):
    qmask=mask[cq]
    x11 = r_q*np.cos(theta)+qmask[0]
    x22 = r_q*np.sin(theta)+qmask[1]
    for c in range(len(x11)):

      xs=x11[c]
      ys=x22[c]

      lines=np.empty((2,1000000), dtype=np.float64)
      lines[:]=np.nan
      stop=0
      nnn=0
      
      lines[0][nnn]=xs
      lines[1][nnn]=ys
      while  abs(xs)<size+2 and abs(ys)<size+2: 
        nnn+=1

        for cq1 in range(len(q_prop)):
          q=q_prop[cq1]
          if ((ys-q[1])**2+(xs-q[0])**2)**0.5<r_q/2 :
            stop=1
            break
        if stop==1:
          break
        dx, dy = E1(q_prop,xs,ys)

        xs+=dx
        ys+=dy
        lines[0][nnn]=xs
        lines[1][nnn]=ys
       
      linen[cq,c,:]=lines.reshape(-1)

  return linen

Interaction entre les charges

Pour refléter leur interaction, il est nécessaire de changer ses coordonnées et sa vitesse après chaque petit temps dt.

x + = \frac{E_{x} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{x} \cdot d t

$x+=\frac{E_x \cdot q \cdot dt^2}{2\cdot m} + v_x\cdot dt$

y + = \frac{E_{y} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{y} \cdot d t

$y+=\frac{E_y \cdot q \cdot dt^2}{2\cdot m} + v_y \cdot dt$

v_{x} + = \frac{E_{x} \cdot q \cdot d t}{m}

$v_x+= \frac{E_x \cdot q \cdot dt}{ m}$

v_{y} + = \frac{E_{y} \cdot q \cdot d t}{m}

$v_y+= \frac{E_y \cdot q \cdot dt}{ m}$

Fonction de mise à jour des coordonnées et des projections des vitesses de charge

def Update_all(q_prop):
  vx=0
  vy=0
  x=0
  y=0
  q_prop_1=np.copy(q_prop)
  for c in range(len(q_prop)):#         
    xs=q_prop[c][0]
    ys=q_prop[c][1]
    q =q_prop[c][2]
    m =q_prop[c][3]
    vx=q_prop[c][4]
    vy=q_prop[c][5]
    Ex, Ey= E(q_prop, xs, ys, c)

    x=(((Ex*q)/m)*dt**2)/2+vx*dt+xs
    y=(((Ey*q)/m)*dt**2)/2+vy*dt+ys
    vx+=((Ex*q)/m)*dt
    vy+=((Ey*q)/m)*dt
    #print(q_prop[c]-[x,y,q,m,vx,vy])
    q_prop_1[c]=[x,y,q,m,vx,vy]
  
  return q_prop_1#

La gravité

Sur la base du code existant, j'ai écrit un simulateur qui reflète les mouvements des corps sous l'influence de la gravité. Les changements dans le code concernent principalement la fonction tension car l'accélération sera désormais envisagée à l'aide d'une formule similaire.

g = \frac{G * m}{r^{2}}

$g=\frac{G*m}{r^2}$

\vec{g} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{g}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{g}}_{i} |}{R_{i}} \end{matrix})

$\vec{g}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{g}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{g}_i|}{R_i} \end{array}\right) \qquad$

Les planètes partent de l'axe des x à la distance du périhélie et à la vitesse du périhélie. Toutes les valeurs des planètes et du soleil (masse, distance, extrémités) du répertoire.

Animation pour les 4 premières planètes + soleil.

En attente de critiques et de suggestions. Au revoir.

Visualisation des lignes de tension et des mouvements des charges électrostatiques, simulation du mouvement planétaire du système solaire

Théorie

Méthode de calcul E

Méthode de construction de ligne

Interaction entre les charges

La gravité

More articles: