👉🏾 🚾 👩🏼‍🏫 Les gens rencontrent des systèmes de recommandation. Factorisation 🆘 💍 🈁

L'apprentissage automatique a pratiquement pénétré notre vie quotidienne. Certains ne sont plus surpris lorsqu'ils sont informés des réseaux de neurones dans leurs smartphones. L'un des grands domaines de cette science est les systèmes de recommandation. Ils sont partout: lorsque vous écoutez de la musique, lisez des livres, regardez des émissions de télévision ou des vidéos. Le développement de cette science a lieu dans des entreprises géantes telles que YouTube , Spotify et Netfilx . Bien sûr, toutes les réalisations scientifiques dans ce domaine sont publiées à la fois lors des célèbres conférences NeurIPS ou ICML , et lors des RecSys un peu moins connus .aiguisé sur ce sujet. Et dans cet article, nous parlerons de l'évolution de cette science, des méthodes utilisées dans les recommandations d'hier et d'aujourd'hui, et des mathématiques derrière tout cela.

Je me suis inspiré pour écrire cet article en travaillant dans le StatML laboratoire à Skoltech liés aux systèmes recommender.

Pourquoi et pour qui cet article

Pourquoi cela peut-il être important pour chacun de nous? Jetez un œil à la liste ci-dessous:

Recommandations vidéo: YouTube, Netlix, HBO, Amazon Prime, Disney +, Hulu, Okko
Recommandations audio: Spotify, Yandex.Music, Yandex.Radio, Apple Music
Recommandations de produit: Amazon, Avito, litres, MyBook
Recommandations de recherche: Google, Yandex, Bing, Yahoo, Mail
: Booking, Twitter, Instagram, ., , GitHub

, . , . , , YouTube.

( ), . , , . , ( ). -, . , -, , - . , . , , , , .

, , , , - . , (, , , ..). , .

, . : $U$ $I$ — . $r_{ui}$ $u$ $i$ . , , , , . :

D = {(u, i) | if \exists r_{u i}, u \in U, i \in I}

$\mathcal{D} = \{ (u, i) |\text{ if } \exists r_{ui}, u \in U, i \in I\}$

$f$ :

f (u, i) = {\hat{r}}_{u i} \approx r_{u i}

$f(u, i) = \hat{r}_{ui}\approx r_{ui}$

, $r_{ui}$ 1 5 ( ) : 1 -1 ( / )

3 :

Content-based (CB)
Collaborative filtering (CF)
Hybrid recommendations

. — , . : — , — , . . , : , ..

, . - , .

. , , , .

, , . . , , . .

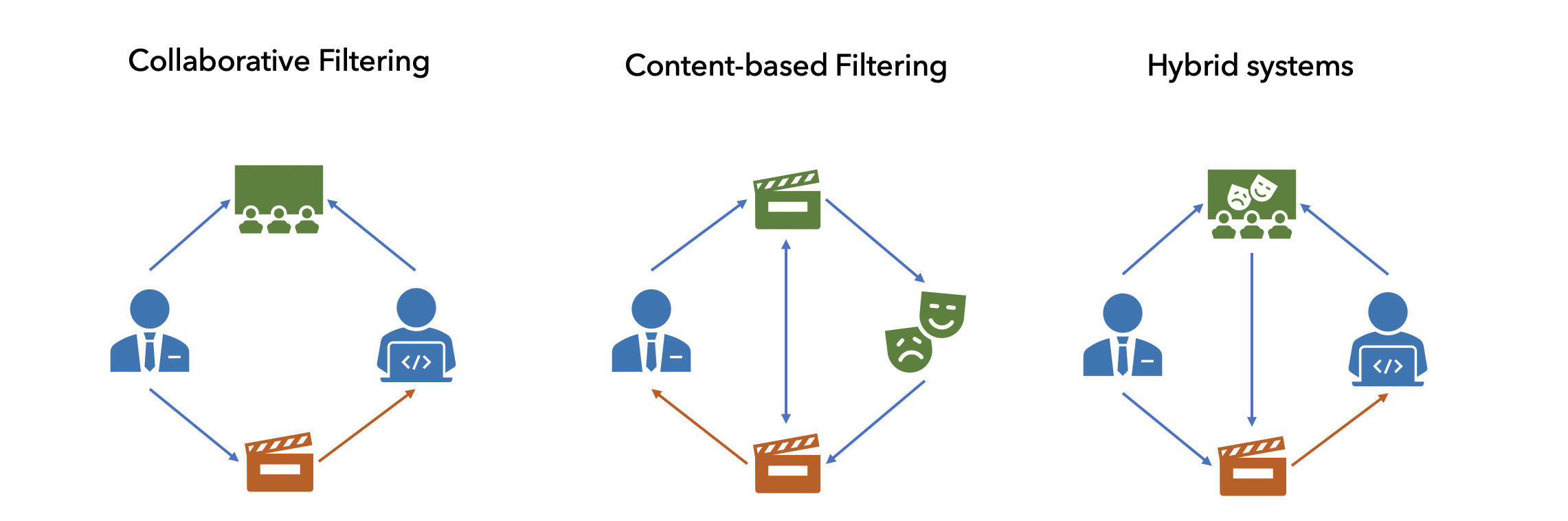
Matrix Factorization

, . : . .

:
- Singular Value Decomposition (SVD)
- Singular Value Decomposition with implicit feedback (SVD++)
- Collaborative Filtering with Temporal Dynamics (TimeSVD++)
- Weighted Matrix Factorization (WMF or ALS)
- Sparse Linear Methods (SLIM)
- Factorization Machines (FM)
:
- Probabilistic Matrix Factorization (PMF)
- Bayesian Probabilistic Matrix Factorization (BPMF)
- Bayesian Factorization Machines (BFM)
- Gaussian Process Factorization Machines (GPFM)

Singular Value Decomposition (SVD)

— SVD. $A$ $n \times m$ , $n = |U|$ , $m = |I|$ . $\mathcal{D}$ $A_{ui} = r_{ui}$ , . SVD , $A$ : $U,~\Sigma,~V$ . $k$ , $A$ .

A = U Σ V^{T}, A \approx \hat{A} = \hat{U} \hat{Σ} {\hat{V}}^{T} .

$A = U \Sigma V^T, \quad\quad\quad\quad A \approx \hat{A} = \hat{U} \hat{ \Sigma } \hat{V}^T .$

$Q$ $P$ . $A$ :

P = (\hat{U} \hat{Σ})^{T}, Q = {\hat{V}}^{T}, A \approx P^{T} \cdot Q .

$P = (\hat{U} \hat{ \Sigma })^T, \quad\quad Q = \hat{V}^T, \quad\quad\quad\quad A \approx P^T \cdot Q .$

r_{u i} \approx {\hat{r}}_{u i} = p_{u}^{T} q_{i} .

$r_{ui} \approx \hat{r}_{ui} = p^T_u q_i .$

, $p_u$ $q_i$ — $u$ $i$ - $k$ . . . :

Θ = {p_{u}, q_{i} | u \in U, i \in I} .

$\Theta = \{ p_u, q_i| u \in U, i \in I\} .$

c :

\sum_{(u, i) \in D} (r_{u i} - {\hat{r}}_{u i})^{2} + λ \sum_{θ \in Θ} ‖ θ ‖^{2} = \sum_{(u, i) \in D} (r_{u i} - p_{u}^{T} q_{i})^{2} + λ \sum_{u \in U} ‖ p_{u} ‖^{2} + λ \sum_{i \in I} ‖ q_{i} ‖^{2} .

$\sum_{(u, i) \in \mathcal{D}} (r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 = \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p^T_u q_i)^2 + \lambda\sum_{u \in U}\|p_u\|^2 + \lambda\sum_{i \in I}\|q_i\|^2 .$

, , , , . $\hat{r}_{ui}$ . (GD) (ALS). Habr- , . , , .

( SVD, SVD $_{bias}$ ). , , . . SVD . (bias):

{\hat{r}}_{u i} = μ + b_{u} + b_{i} + p_{u}^{T} q_{i},

$\hat{r}_{ui} =\mu + b_u + b_i + p^T_u q_i ,$

$b_u$ — , $b_i$ — , $\mu$ — . :

Θ = {μ, b_{u}, b_{i}, p_{u}, q_{i} | u \in U, i \in I} .

$\Theta = \{ \mu, b_u, b_i, p_u, q_i| u \in U, i \in I\} .$

SVD++

Factorization Meets the Neighborhood SVD . (explicit and implicit user feedback). $r_{ui}$ , . . : $R(u)$ — ( ) $N(u)$ — ( ).

SVD++ :

{\hat{r}}_{u i} = μ + b_{u} + b_{i} + q_{i}^{T} (p_{u} + | N (u) |^{- 1 / 2} \sum_{j \in N (u)} y_{j}) .

$\hat{r}_{ui} =\mu + b_u + b_i + q^T_i \left( p_u + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) .$

Θ = {μ, b_{u}, b_{i}, p_{u}, q_{i}, y_{i} | u \in U, i \in I} .

$\Theta = \{ \mu, b_u, b_i, p_u, q_i, y_i| u \in U, i \in I\} .$

, $N(u)$ $R(u)$ , .. $R(u) \subset N(u)$ . (item-item recommendation).

Asymmetric-SVD

SVD++ . . :

{\hat{r}}_{u i} = b_{u i} + q_{i}^{T} (| R (u) |^{- 1 / 2} \sum_{j \in R (u)} (r_{u j} - b_{u j}) x_{j} + | N (u) |^{- 1 / 2} \sum_{j \in N (u)} y_{j}),

$\hat{r}_{ui} = b_{ui} + q^T_i \left( |R(u)|^{-1/2} \sum_{j \in R(u)} (r_{uj} - b_{uj})x_j + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) ,$

$b_{ui} = \mu + b_u + b_i$

TimeSVD++

TimeSVD++. (MovieLens, Netflix) , . , . Collaborative Filtering with Temporal Dynamics SVD++ :

{\hat{r}}_{u i} (t) = μ + b_{u} (t) + b_{i} (t) + q_{i}^{T} (p_{u} (t) + | R (u) |^{- 1 / 2} \sum_{j \in R (u)} y_{j}) .

$\hat{r}_{ui}(t) =\mu + b_u(t) + b_i(t) + q^T_i \left( p_u(t) + |R(u)|^{-1/2} \sum_{j \in R(u)} y_j \right) .$

Voyons comment exactement le temps affecte chaque terme:
Biais de l'élément: Si vous divisez l'intervalle de temps lorsque les notes ont été mises en segments (30 parties sont proposées dans le travail) et ajoutez vos propres paramètres $b_{i,\text{Bin}(t)}$ pour chaque produit, qui sont sélectionnés en fonction de l'intervalle dans lequel la variable $t$ :

b_{i} (t) = b_{i} + b_{i, Bin (t)}

$b_i(t) = b_i + b_{i, \text{Bin}(t)}$

Biais des utilisateurs: en analysant les données de Neflix, nous avons remarqué que pour chaque utilisateur en moyenne il n'y a que 40 jours au cours desquels il s'est classé. Par conséquent, nous agirons comme pour les marchandises et ajouterons nos propres paramètres

b_{u, t}

$b_{u, t}$ pour chaque utilisateur. Nous ajoutons une dépendance linéaire au temps - nous introduisons un terme supplémentaire

α_{u}

$\alpha_u$ avec taux d'amortissement:

b_{i} (t) = b_{i} + α_{u} \cdot {dev}_{u} (t) + b_{u, t} {dev}_{u} (t) = sign (t - t_{u}) \cdot | t - t_{u} |^{β}

$b_i(t) = b_i + \alpha_u \cdot \text{dev}_u(t) + b_{u, t} \quad\quad\quad\quad \text{dev}_u(t) = \text{sign}(t - t_u) \cdot |t - t_u|^{\beta}$

.
Il existe d'autres options pour ajouter une dépendance temporelle aux utilisateurs: Plus de détails sont décrits dans l'article
Intégrations d'utilisateurs: nous ajouterons une astuce similaire pour chaque composant de notre représentation latente

p_{u} (t) = (p_{u 1} (t), \dots, p_{u f} (t))^{T}

$p_u(t) = (p_{u1}(t), \dots, p_{uf}(t))^T$ :

p_{u k} (t) = p_{u k} + α_{u k} \cdot {dev}_{u} (t) + p_{u k, t} .

$p_{uk}(t) = p_{uk} + \alpha_{uk} \cdot \text{dev}_u(t) + p_{uk, t}.$

Factorisation à matrice pondérée (WMF) et moindres carrés alternés (ALS)

L'un des principaux problèmes rencontrés par SVD est l'utilisation d'une réponse explicite de l'utilisateur uniquement. Ce problème a été partiellement résolu dans SVD ++ . Mais il existe un autre moyen: la factorisation matricielle pondérée ( WMF ). Dans cet article, ils ont suggéré de ne presque pas changer le modèle ( $\hat{r}_{ui} = p^T_u q_i$ ) et changer le processus d'apprentissage. Attribuer des notes $r_{ui}$ que nous ne savons pas (c'est-à-dire pour les couples $(u, i) \notin \mathcal{D}$ ) la valeur est 0. Et puis pour chaque paire $(u, i)$ entrez le paramètre $c_{ui}$ , $r_{ui}$ . , . - . YouTube , . , , , . , , , :

\sum_{(u, i)} c_{u i} (r_{u i} - {\hat{r}}_{u i})^{2} + λ \sum_{θ \in Θ} ‖ θ ‖^{2} .

$\sum_{(u, i)} c_{ui}(r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 .$

: $c_{ui} = 1 + \alpha r_{ui}$ . : $r_{ui}>0$ $r_{ui} = 0$ . $\alpha$ $\alpha = 40$ .

, (ALS) . WMF, ALS, .

Fast Alternating Least Squares

ALS , eALS . , . , . .

, $c_{ui}$ ALS :

c_{u i} = c_{i} + α r_{u i}, c_{i} = c_{0} \frac{f_{i}^{β}}{\sum_{j \in I} f_{j}^{β}},

$c_{ui} = c_i + \alpha r_{ui}, \quad\quad\quad\quad c_i = c_0 \frac{f_i^{\beta}}{\sum_{j \in I} f_j^{\beta}} ,$

$c_0$ $\beta$ , .

Sparse Linear Methods (SLIM)

Sparse Linear Methods (SLIM) . , SVD . . SLIM :

{\hat{a}}_{u i} = a_{u}^{T} w_{i} \hat{A} = A W

$\hat{a}_{ui} = a^T_u w_i \quad\quad\quad\quad \hat{A} = AW$

$W \in \mathbb{R}^{m \times m}$ . : $W \geq 0$ $\text{diag}(W) = 0$ . :

\frac{1}{2} ‖ A - A W ‖_{F}^{2} + \frac{β}{2} ‖ W ‖_{F}^{2} + λ ‖ W ‖_{1}

$\frac{1}{2}\|A - AW\|^2_F + \frac{\beta}{2}\|W\|^2_F + \lambda\|W\|_1$

$W$ .

Factorization Machines (FM)

, Factorization Machines (FM). , ( 2- ). :

\hat{r} (x) = w_{0} + \sum_{i = 1}^{n} w_{i} x_{i} + \sum_{i = 1}^{n} \sum_{i = j + 1}^{n} v_{i}^{T} v_{j} x_{i} x_{j}, w_{0} \in R w \in R^{n} V \in R^{n \times k} .

$\hat{r}(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{i=j+1}^{n} v^T_i v_j ~ x_i x_j, \quad\quad\quad\quad w_0 \in \mathbb{R} ~~~ w \in \mathbb{R}^n ~~~ V \in \mathbb{R}^{n \times k} .$

(SGD) ( ). , $x$ $(u, i)$ . . , — . — ( ). ( ).

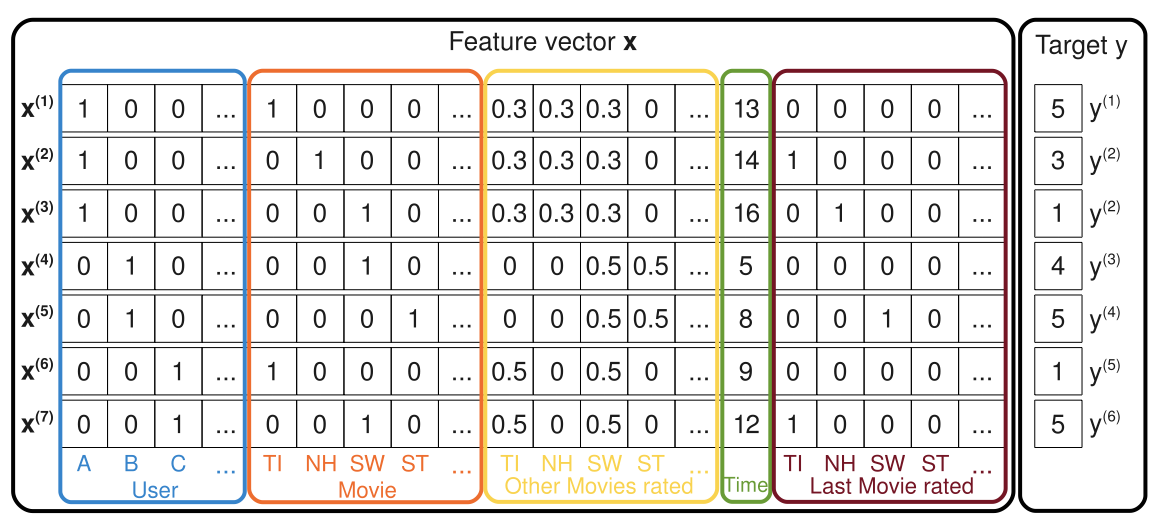
, SVD, SVD++ — FM. SVD , :

n = | U \cup I |, x_{j} = δ (j = u \lor j = i) .

$n = | U \cup I |, \quad\quad\quad x_j = \delta (j = u ~\lor~ j = i) .$

$\delta$ — . .. $x$ $u$ $i$ . FM :

\hat{r} (x) = w_{0} + w_{u} + w_{i} + v_{u}^{T} v_{i} .

$\hat{r}(x) = w_0 + w_u + w_i + v^T_u v_i .$

, $x$ : , . , , , , , , . .

Probabilistic Matrix Factorization (PMF)

, , , .

(PMF), . , SVD: $p_u$ $q_i$ — . , :

p (r | P, Q, σ) = \prod_{(u, i) \in D} N (r_{u i} | g (p_{u}^{T} q_{i}), σ^{2}),

$p(r | P, Q, \sigma) = \prod_{(u, i) \in \mathcal{D}}\mathcal{N}(r_{ui}| g(p_u^Tq_i), \sigma^2) ,$

$\mathcal{N}$ — , a $g(x) = \frac{1}{1 + e^{-x}}$ — (). , , :

p (P | σ_{p}) = \prod_{u \in U} p (p_{u} | 0, σ_{p}^{2} I), p (Q | σ_{q}^{2}) = \prod_{i \in I} p (q_{i} | 0, σ_{q}^{2} I) .

$p(P| \sigma_p) = \prod_{u \in U} p(p_u| 0, \sigma^2_p \mathbf{I}), \quad\quad\quad\quad p(Q| \sigma^2_q) = \prod_{i \in I} p(q_i| 0, \sigma_q^2 \mathbf{I}) .$

( ) , :

\frac{1}{2} \sum_{(u, i) \in D} (r_{u i} - p_{u}^{T} q_{i})^{2} + \frac{λ_{p}}{2} \sum_{u \in U} ‖ p_{u} ‖^{2} + \frac{λ_{q}}{2} \sum_{i \in I} ‖ q_{i} ‖^{2},

$\frac{1}{2} \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p_u^T q_i)^2 + \frac{\lambda_p}{2} \sum_{u \in U} \|p_u\|^2 + \frac{\lambda_q}{2} \sum_{i \in I} \|q_i\|^2 ,$

$\lambda_p = \frac{\sigma_p}{\sigma}$ $\lambda_q = \frac{\sigma_q}{\sigma}$ — . , SVD , .

Constrained PMF

PMF Constrained PMF. , SVD SVD++. , , $p_u$ :

p_{u} + \frac{\sum_{i \in R (u)} y_{i}}{| R (u) |},

$p_u + \frac{\sum_{i \in R(u)} y_i}{|R(u)|} ,$

$R(u)$ — , $u$ .

Bayesian Probabilistic Matrix Factorization (BPMF)

PMF BPMF. PMF , , . :

p (P | μ_{p}, Λ_{p}) = \prod_{u \in U} p (p_{u} | μ_{p}, Λ_{p}), p (Q | μ_{q}, Λ_{q}) = \prod_{i \in I} p (q_{i} | μ_{q}, Λ_{q}) .

$p(P| \mu_p, \Lambda_p) = \prod_{u \in U} p(p_u| \mu_p, \Lambda_p) ,\quad\quad\quad\quad p(Q| \mu_q, \Lambda_q) = \prod_{i \in I} p(q_i| \mu_q, \Lambda_q) .$

$\Theta_p = \{ \mu_p, \Lambda_p \}$ $\Theta_q = \{ \mu_q, \Lambda_q \}$ - $\Theta_0 = \{ \mu_0, \nu_0, W_0 \}$ . , .

Bayesian Factorization Machines (BFM)

, Bayesian, . , $\Theta = \{ w_0, w_i, v_i\} .$ , - . : $\Theta_H = \{ \lambda_{\theta}, \mu_{\theta} | \theta \in \Theta \}$ . .

Gaussian Process Factorization Machines (GPFM)

GPFM . $f$ $\theta$ . $\theta_u$ , , :

{\hat{r}}_{u i} = f (q_{i}, θ_{u})

$\hat{r}_{ui} = f(q_i, \theta_u)$

, . , $f$ , . , , , .

: Bayesian Personalized Ranking (BPR)

BPR , "". , BPR — , , Bayesian Personalized Ranking. . , , $i$ $j$ $u$ . $(u, i)$ $r_{ui}$ $(u, i, j)$ $i$ $j$ ((+) $i$ , $j$ (-) ). $\mathcal{D}_S$ . . ( personalized ):

p (i <_{u} j | Θ) = σ ({\hat{r}}_{u i j} (Θ)),

$p(i <_u j | \Theta) = \sigma(\hat{r}_{uij}(\Theta)) ,$

$\sigma$ — , a $\hat{r}_{uij}$ — . (MLE), , :

min_{Θ} \sum_{(u, i, j) \in D_{S}} \ln σ ({\hat{r}}_{u i j}) - λ ‖ Θ ‖^{2}

$\min_{\Theta} \sum_{(u, i, j) \in \mathcal{D}_S}\ln{\sigma(\hat{r}_{uij})} - \lambda \|\Theta\|^2$

(SGD):

Θ \leftarrow Θ + α (\frac{e^{- {\hat{r}}_{u i j}}}{1 + e^{- {\hat{r}}_{u i j}}} \cdot \frac{\partial}{\partial Θ} {\hat{r}}_{u i j} + λ Θ)

$\Theta \leftarrow \Theta + \alpha\left(\frac{e^{-\hat{r}_{uij}}}{1 + e^{-\hat{r}_{uij}}} \cdot \frac{\partial}{\partial \Theta}\hat{r}_{uij} + \lambda \Theta \right)$

, . , , . SVD:

{\hat{r}}_{u i j} = {\hat{r}}_{u i} - {\hat{r}}_{u j} {\hat{r}}_{u i} = p_{u}^{T} q_{i}

$\hat{r}_{uij} = \hat{r}_{ui} - \hat{r}_{uj} \quad\quad\quad\quad \hat{r}_{ui} = p_u^T q_i$

\frac{\partial}{\partial Θ} {\hat{r}}_{u i j} = {\begin{cases} (q_{i k} - q_{j k}) if θ = p_{u k} \\ p_{u k} if θ = q_{i k} \\ - p_{u k} if θ = q_{j k} \end{cases}

$\frac{\partial}{\partial \Theta}\hat{r}_{uij} =\begin{cases} (q_{ik} - q_{jk})~~~\text{if } \theta = p_{uk}\\ p_{uk}~~~~~~~~~~~~~~~\text{if } \theta = q_{ik}\\ -p_{uk}~~~~~~~~~~~~\text{if } \theta = q_{jk} \end{cases}$

BPR ( ) , . , . . , (pairwise approach) (pointwise approach). . , 5 , . , , . — BPR - , . , .

Show must go on

Cette fois, nous avons discuté de nombreuses méthodes de factorisation dans les systèmes de recommandation, mais les réseaux de graphes et de neurones , qui ont également beaucoup de choses intéressantes , sont restés intacts .

Les gens rencontrent des systèmes de recommandation. Factorisation