Buen día.Le presento la traducción del artículo "Algoritmos en gráficos: Hablemos de la búsqueda de profundidad primero (DFS) y de búsqueda de amplitud primero (BFS)" por Try Khov.¿Qué es un recorrido de gráfico?
En palabras simples, un recorrido de gráfico es una transición de uno de sus vértices a otro en busca de las propiedades de conexión de estos vértices. Los enlaces (líneas que conectan vértices) se denominan direcciones, caminos, caras o bordes de un gráfico. Los vértices del gráfico también se denominan nodos.Los dos algoritmos principales de recorrido del gráfico son Profund-First Search, DFS y Breadth-First Search, BFS.A pesar de que ambos algoritmos se utilizan para atravesar el gráfico, tienen algunas diferencias. Comencemos con DFS.Búsqueda de profundidad
DFS sigue el concepto de "ir profundo, cabeza primero". La idea es que nos movemos desde el pico inicial (punto, lugar) en cierta dirección (a lo largo de un cierto camino) hasta llegar al final del camino o destino (pico deseado). Si hemos llegado al final del camino, pero no es un destino, entonces volvemos (hasta el punto de ramificar o divergir caminos) y seguimos una ruta diferente.Veamos un ejemplo. Supongamos que tenemos un gráfico dirigido que se ve así:
Estamos en el punto "s" y necesitamos encontrar el vértice "t". Usando DFS, investigamos uno de los posibles caminos, avanzamos hasta el final y, si no encontramos t, regresamos y exploramos otro camino. Así es como se ve el proceso:
Aquí nos movemos a lo largo del camino (p1) hasta el pico más cercano y vemos que este no es el final del camino. Por lo tanto, pasamos al siguiente pico.
Llegamos al final de p1, pero no encontramos t, por lo que volvemos a sy avanzamos por el segundo camino.
Habiendo alcanzado la parte superior de la ruta "p2" más cercana al punto "s", vemos tres direcciones posibles para un mayor movimiento. Como ya hemos visitado el pico que corona la primera dirección, avanzamos por la segunda.
Nuevamente llegamos al final del camino, pero no encontramos t, así que volvemos. Seguimos el tercer camino y, finalmente, alcanzamos el pico deseado "t".
Así es como funciona DFS. Nos movemos por un cierto camino hasta el final. Si el final del camino es el pico deseado, hemos terminado. Si no, regrese y avance por un camino diferente hasta que exploremos todas las opciones.Seguimos este algoritmo para cada vértice visitado.La necesidad de repetición repetida del procedimiento indica la necesidad de utilizar la recursividad para implementar el algoritmo.Aquí está el código JavaScript:
function dfs(adj, v, t) {
if(v === t) return true
if(v.visited) return false
v.visited = true
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
let reached = dfs(adj, neighbor, t)
if(reached) return true
}
}
return false
}
Nota: Este algoritmo especial DFS le permite verificar si es posible llegar de un lugar a otro. DFS se puede utilizar para diversos fines. Estos objetivos determinarán cómo se verá el algoritmo en sí. Sin embargo, el concepto general se ve exactamente así.Análisis DFS
Analicemos este algoritmo. Dado que vamos alrededor de cada "vecino" de cada nodo, ignorando los que visitamos anteriormente, tenemos un tiempo de ejecución igual a O (V + E).Una breve explicación de lo que significa V + E:V es el número total de vértices. E es el número total de caras (aristas).Puede parecer más apropiado usar V * E, pero pensemos qué significa V * E.V * E significa que con respecto a cada vértice, debemos investigar todas las caras del gráfico, independientemente de si estas caras pertenecen a un vértice particular.Por otro lado, V + E significa que para cada vértice evaluamos solo los bordes adyacentes. Volviendo al ejemplo, cada vértice tiene un cierto número de caras y, en el peor de los casos, rodeamos todos los vértices (O (V)) y examinamos todas las caras (O (E)). Tenemos vértices V y caras E, por lo que obtenemos V + E.Además, dado que usamos la recursión para atravesar cada vértice, esto significa que se usa una pila (la recursión infinita conduce a un error de desbordamiento de la pila). Por lo tanto, la complejidad espacial es O (V).Ahora considere el BFS.Amplia búsqueda
BFS sigue el concepto de "expandirse ampliamente, elevándose a la altura del vuelo de un pájaro" ("ir ancho, a vista de pájaro"). En lugar de avanzar a lo largo de un cierto camino hacia el final, BFS implica avanzar un vecino a la vez. Esto significa lo siguiente: enlugar de seguir la ruta, BFS significa visitar a los vecinos más cercanos a s en una sola acción (paso), luego visitar a los vecinos de los vecinos y así sucesivamente hasta que se detecte t.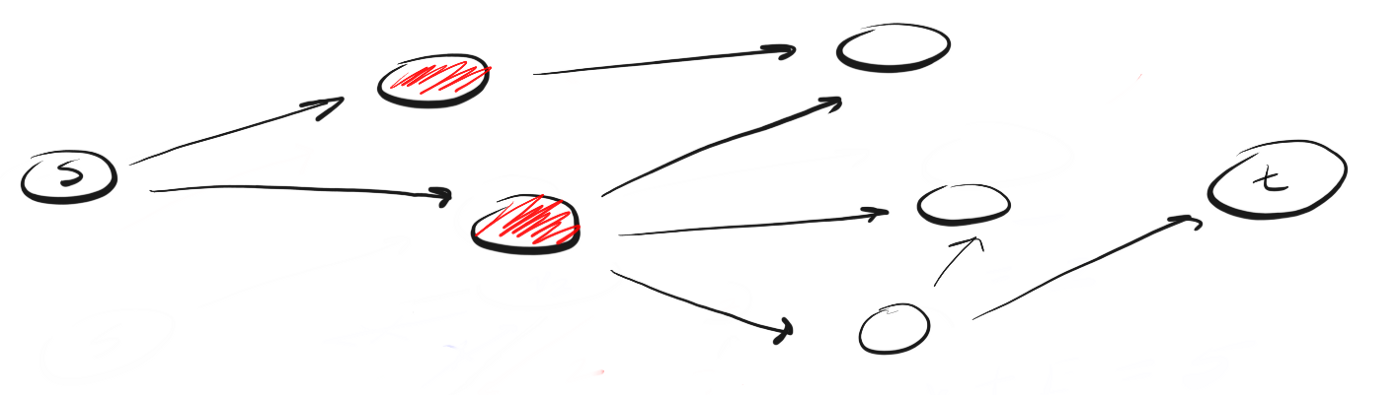
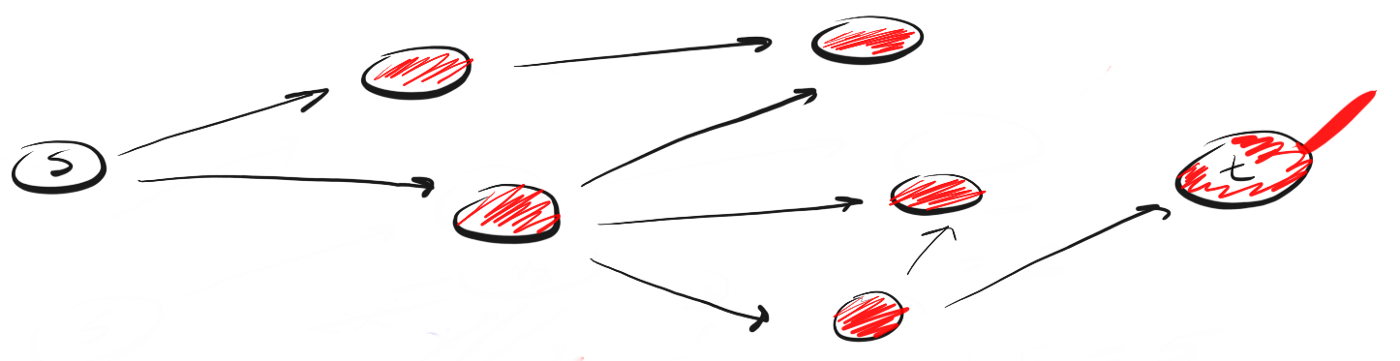¿En qué se diferencia DFS de BFS? Me gusta pensar que DFS sigue adelante, y BFS no tiene prisa, pero estudia todo en un solo paso.Entonces surge la pregunta: ¿cómo saber qué vecinos deben visitarse primero?Para hacer esto, podemos usar el concepto de "primero en entrar, primero en salir" (primero en entrar, primero en salir, FIFO) de la cola. Primero ponemos en cola el pico más cercano a nosotros, luego sus vecinos no visitados, y continuamos este proceso hasta que la cola esté vacía o hasta que encontremos el vértice que estamos buscando.Aquí está el código:
function bfs(adj, s, t) {
let queue = []
queue.push(s)
s.visited = true
while(queue.length > 0) {
let v = queue.shift()
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
queue.push(neighbor)
neighbor.visited = true
if(neighbor === t) return true
}
}
}
return false
}
Análisis BFS
Puede parecer que BFS es más lento. Sin embargo, si observa de cerca las visualizaciones, puede ver que tienen el mismo tiempo de ejecución.Una cola implica procesar cada vértice antes de llegar a un destino. Esto significa que, en el peor de los casos, BFS explora todos los vértices y caras.A pesar del hecho de que BFS puede parecer más lento, en realidad es más rápido, porque cuando se trabaja con gráficos grandes se descubre que DFS pasa mucho tiempo siguiendo caminos que finalmente resultan ser falsos. BFS se usa a menudo para encontrar el camino más corto entre dos picos.Por lo tanto, el tiempo de ejecución BFS también es O (V + E), y dado que utilizamos una cola que contiene todos los vértices, su complejidad espacial es O (V).Analogías de la vida real
Si da analogías de la vida real, así es como me imagino el trabajo de DFS y BFS.Cuando pienso en DFS, imagino un ratón en un laberinto en busca de comida. Para llegar al objetivo, el ratón se ve obligado a correr en un callejón sin salida muchas veces, regresar y moverse de una manera diferente, y así sucesivamente hasta que encuentre una salida del laberinto o la comida.
Una versión simplificada se ve así: a
su vez, cuando pienso en BFS, imagino círculos en el agua. La caída de una piedra al agua conduce a la propagación de disturbios (círculos) en todas las direcciones desde el centro.
Una versión simplificada se ve así:
recomendaciones
- Las búsquedas de profundidad y amplitud se utilizan para recorrer el gráfico.
- DFS se mueve a lo largo de los bordes hacia adelante y hacia atrás, y BFS se extiende a través de los vecinos en busca de un objetivo.
- DFS usa la pila y BFS la cola.
- El tiempo de ejecución de ambos es O (V + E), y la complejidad espacial es O (V).
- Estos algoritmos tienen una filosofía diferente, pero son igualmente importantes para trabajar con gráficos.
Nota Per.: No soy especialista en algoritmos y estructuras de datos, por lo tanto, si se encuentran errores, inexactitudes o formulaciones incorrectas, escriba una carta personal para su corrección y aclaración. Estaré agradecido.Gracias por su atención.