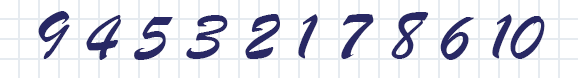May resultó frío, la calefacción estaba apagada y los poderes informáticos (y de calefacción) no eran ninguno, pero estaban inactivos. Entonces, ¿por qué no cargarlos con algo inútil , que los calentará y entretendrá?Pero comenzaré desde lejos. El otro día, me encontré con un problema para una escuela secundaria con la siguiente redacción: “Varios enteros positivos consecutivos se escribieron en una fila de tal manera que la suma de cada tres números consecutivos se divide completamente por el número más a la izquierda de este triple. "¿Cuál es el número máximo de números que podrían escribirse si el último número de línea es impar?”Con esta restricción, es fácil demostrar que en cada triple de números impares habrá más que números pares. Y dado que la diferencia entre ellos no puede ser más de uno, la longitud máxima de la secuencia está limitada a cinco números. Y como ejemplo, podemos dar la secuencia 4 5 3 2 1 .La prueba detallada se puede encontrar aquí.Pero, ¿qué pasa si eliminamos la restricción indicada sobre la rareza del último número? Luego, a la derecha, puede agregar los números 7 6 8 , expandiendo la secuencia a ocho números. También puede agregar una docena y adjuntar los nueve que faltan a la izquierda. Bueno, y probablemente esta no sea la única permutación ni la más larga.En realidad, tratando de razonar lógicamente, no encontré evidencia de las limitaciones de tales secuencias y decidí involucrar una calculadora en el calentador doméstico para su análisis . Rough búsqueda exhaustiva de todos los N ! Las opciones mostraron rápidamente la falla del método, pero la enumeración direccional permitió un progreso significativo, y el resultado fue tanto esperado como inesperado al mismo tiempo.Resultó que para todo N hasta 29 inclusive, tales permutaciones de números del 1 al N se encuentran, sin embargo, para longitudes 27 y 29 en una sola variante. Pero luego hay lagunas. Para las permutaciones con tamaños 30, 31, 32 y 33, no hay soluciones; para el número 34, hay una.tal33 23 10 13 7 6 1 29 27 2 25 21 4 17 15 19 11 8 3 5 31 9 22 14 30 26 34 18 16 20 12 28 32 24
Por otra parte, dos espacios. Para los valores 37 y 38, tales secuencias no son únicas, y luego fallan. Incluso estaba desesperado, los siguientes diez resultaron estar completamente vacíos, pero la suerte sonrió, para N = 51 todavía se encuentra la permutación necesaria.aqui esta ella46 45 1 44 49 39 10 29 21 37 5 32 23 41 51 31 20 11 9 2 43 35 8 27 13 14 25 3 47 40 7 33 16 17 15 19 26 50 28 22 6 38 34 4 30 18 42 48 36 12 24
Incluso hay dos de ellos, pero se cruzan en su mayor parte.Además, el vacío se planea nuevamente, al menos para los números 52 y 53 no hay soluciones, pero no busqué más. Sin embargo, con cada paso, el tiempo de espera está creciendo exponencialmente, y la casa ya se ha vuelto mucho más cálida, decidí parar allí por ahora.Si reduce el número encontrado de opciones posibles en una tabla, puede construir el siguiente cuadro
Bueno, sí, hay algo en lo que meditar.En el problema original, no había ningún requisito para comenzar la serie natural desde una. Lo principal es que todos los números de a a b se encuentran en la secuencia. Pero lo intenté, solo empeora, hay aún menos opciones. Lo que, de hecho, es explicable. Cuanto mayor sea el número en la posición izquierda de los tres, menor será la multiplicidad obtenida por la suma de los otros dos, es decir las menos opciones disponibles Bueno, la cuestión del límite superior de las longitudes de tales secuencias permanece abierta. Con el crecimiento de la dimensionalidad, la probabilidad de éxito se reduce claramente, pero ¿se anula? O más aún, aunque raramente, se encontrarán con permutaciones (des) interesantes.Finalmente, quizás pueda traer el código del programa de calefacción,cierto él está en Haskellimport Data.List (delete)
import Control.Parallel.Strategies
import System.Environment
pvc :: Int -> Int -> [Int] -> [[Int]]
pvc a b [] = [[a,b]]
pvc a b xs = [a:ys |
x <- xs,
mod (a + b + x) a == 0,
ys <- pvc b x (delete x xs)]
gen :: Int -> [[[Int]]]
gen n =
let ab = [(a, b) | a <- [1..n], b <- delete a [1..n]]
in map hlp ab `using` parList rseq
where
hlp (a,b) = pvc a b $ delete a $ delete b [1..n]
main = do
[n] <- getArgs
print $ concat $ gen $ read n