El guilloquis es un patrón característico del papel moneda y otros valores. Una historia detallada sobre ellos con una digresión en la historia se puede encontrar en el artículo anterior . Allí también se proporcionó un algoritmo de dibujo que construye líneas entrecruzadas por puntos.Bastante inútil, debe tenerse en cuenta si los dibujamos no solo por diversión, sino también con fines prácticos, por ejemplo, para agregar esos valores al diseño. Miles de puntos solo ralentizarán al editor, pero de todos modos no podrá mostrar el resultado; en lugar de líneas continuas reales, habrá algún tipo de resultado de promediar los puntos, hecho como Dios pondría un alma.Por lo tanto, ha llegado el momento de pensar en otro algoritmo, que inmediatamente daría vectores. Dado que los editores comunes para líneas curvas solo ofrecen interpolación por curvas de Bezier, nos centraremos en ellas.El algoritmo, de hecho, es simple, y mucho más simple que el descrito en la primera parte. Tomamos dos curvas envolventes, establecemos el número de ondas que deben caber en 360 grados, estimamos a qué ángulo y con qué curvatura el guilloché real debe ir desde el punto actual al siguiente, e interpolarlo con cuatro curvas de Bezier.Aquí hay un programa en asíntota, que es extremadamente conveniente para tales cosas.import graph;
size(1000,1000);
xaxis(ticks=Ticks);
yaxis(ticks=Ticks);
defaultpen(2);
var zero = (0,0);
real tens(bool at_top, real angle)
{
return angle/180;
}
guide wave(path top, path bottom, int parts, real offset)
{
guide w;
real step = 1/parts;
real half = step/2;
pair[] top_pt;
pair[] bot_pt;
pair[] top_dir;
pair[] bot_dir;
real[] top_angle;
real[] bot_angle;
for(int i: sequence(0,parts-1))
{
real rel = i*step + step*offset;
real top_time = reltime(top, rel);
real bot_time = reltime(bottom, rel+half);
top_pt[i] = point(top, top_time);
bot_pt[i] = point(bottom, bot_time);
top_dir[i] = dir(top, top_time);
bot_dir[i] = dir(bottom, bot_time);
}
for(int i: sequence(0,parts-1))
{
int prev = i == 0 ? parts-1 : i-1;
int next = i == parts-1 ? 0 : i+1;
var v1 = bot_pt[i] - top_pt[i];
var v2 = bot_pt[prev] - top_pt[i];
var a = degrees(v2) - degrees(v1);
top_angle[i] = a<0 ? 360+a : a;
v1 = top_pt[i] - bot_pt[i];
v2 = top_pt[next] - bot_pt[i];
a = degrees(v2) - degrees(v1);
bot_angle[i] = a<0 ? 360+a : a;
}
for(int i: sequence(0,parts-1))
{
int next = i == parts-1 ? 0 : i+1;
var l1 = length(top_pt[i]--bot_pt[i]);
pair ctl1 = top_pt[i] + top_dir[i] * tens(true, top_angle[i]) * l1;
pair ctl2 = bot_pt[i] - bot_dir[i] * tens(false, bot_angle[i]) * l1;
w = w .. top_pt[i] .. controls ctl1 and ctl2 .. bot_pt[i];
var l2 = length(bot_pt[i]--top_pt[next]);
ctl1 = bot_pt[i] + bot_dir[i] * tens(false, bot_angle[i]) * l2;
ctl2 = top_pt[next] - top_dir[next] * tens(true, top_angle[next]) * l2;
w = w .. bot_pt[i] .. controls ctl1 and ctl2 .. top_pt[next];
}
return w;
}
void repeat(int count, path top, path bottom, int parts)
{
real step = 1/count;
for(int i: sequence(0, count-1))
{
draw(wave(top, bottom, parts, step*i));
}
}
path normalize(path p)
{
var min = min(p);
var max = max(p);
var top_center = min + ((max.x-min.x)/2, (max.y-min.y)/2);
return scale(20*1/(max-min).x)*shift(zero - top_center)*p;
}
path top = (338.499521684,-159.274266483)
..controls (327.252951684,-158.148796483) and (323.448961684,-145.618286483) .. (318.743661684,-137.260595483)
..controls (309.897671684,-123.808725483) and (292.025851684,-123.657732483) .. (278.251471684,-118.807470483)
..controls (272.669581684,-117.510629483) and (268.731931684,-109.221757483) .. (274.571781684,-105.645360483)
..controls (281.545351684,-101.031122483) and (290.488261684,-97.7906864833) .. (293.317871684,-89.0437964838)
..controls (296.611021684,-81.8498064838) and (293.894071684,-73.5853264838) .. (295.556161684,-66.3445764838)
..controls (299.563831684,-59.7686064838) and (308.181311684,-64.5344964838) .. (312.903811684,-67.4344264838)
..controls (325.368171684,-74.9872364838) and (341.157891684,-80.6126364838) .. (355.257331684,-73.9383264838)
..controls (363.506651684,-70.9246164838) and (370.115991684,-63.9703964838) .. (378.731941684,-62.0926264838)
..controls (384.688491684,-61.4010364838) and (389.980631684,-67.6129964838) .. (387.306161684,-73.3211464838)
..controls (385.256921684,-82.8346964838) and (388.441441684,-93.9447564833) .. (397.757331684,-98.3016064833)
..controls (403.144721684,-101.085582483) and (412.671611684,-104.606352483) .. (410.331551684,-112.414892483)
..controls (406.654931684,-119.718595483) and (396.921641684,-119.937732483) .. (390.144051684,-122.524267483)
..controls (378.065751684,-125.483516483) and (364.313841684,-130.717262483) .. (359.884541684,-143.562216483)
..controls (356.731021684,-151.157386483) and (350.818391684,-160.192046483) .. (341.435061684,-159.293796483)
..controls (340.456461684,-159.306096483) and (339.478031684,-159.281196483) .. (338.499521684,-159.274296483)
--cycle;
top = normalize(top);
bottom = scale(0.5)*top;
top = ellipse(zero, 4, 6);
bottom = ellipse(zero, 2, 3);
top = circle(zero, 5);
bottom = circle(zero, 3);
repeat(12, top, bottom, 8);
El caso más comprensible es cuando las sinusoides se encuentran entre dos círculos.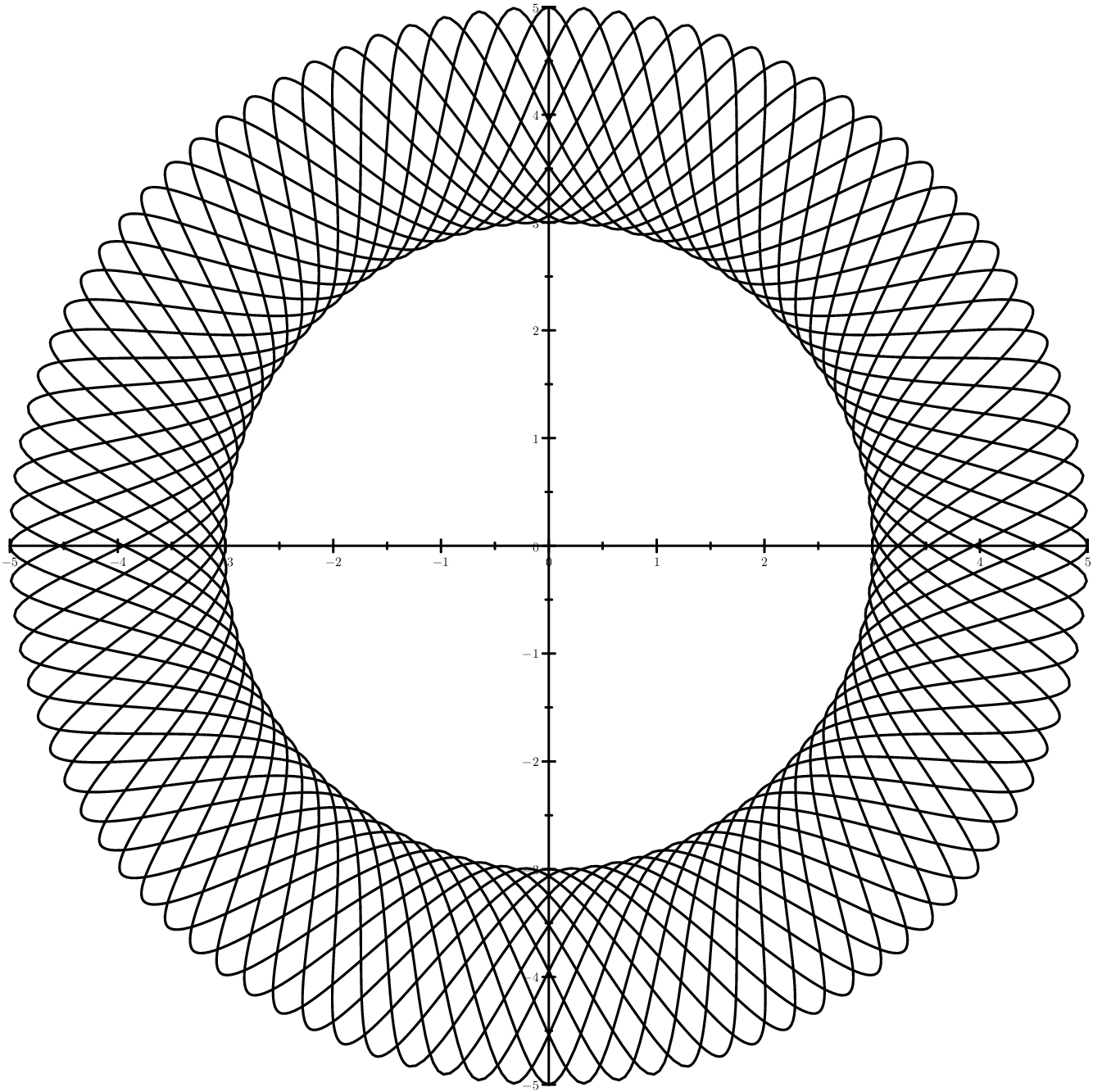
El caso es más astuto: elipses en lugar de círculos.
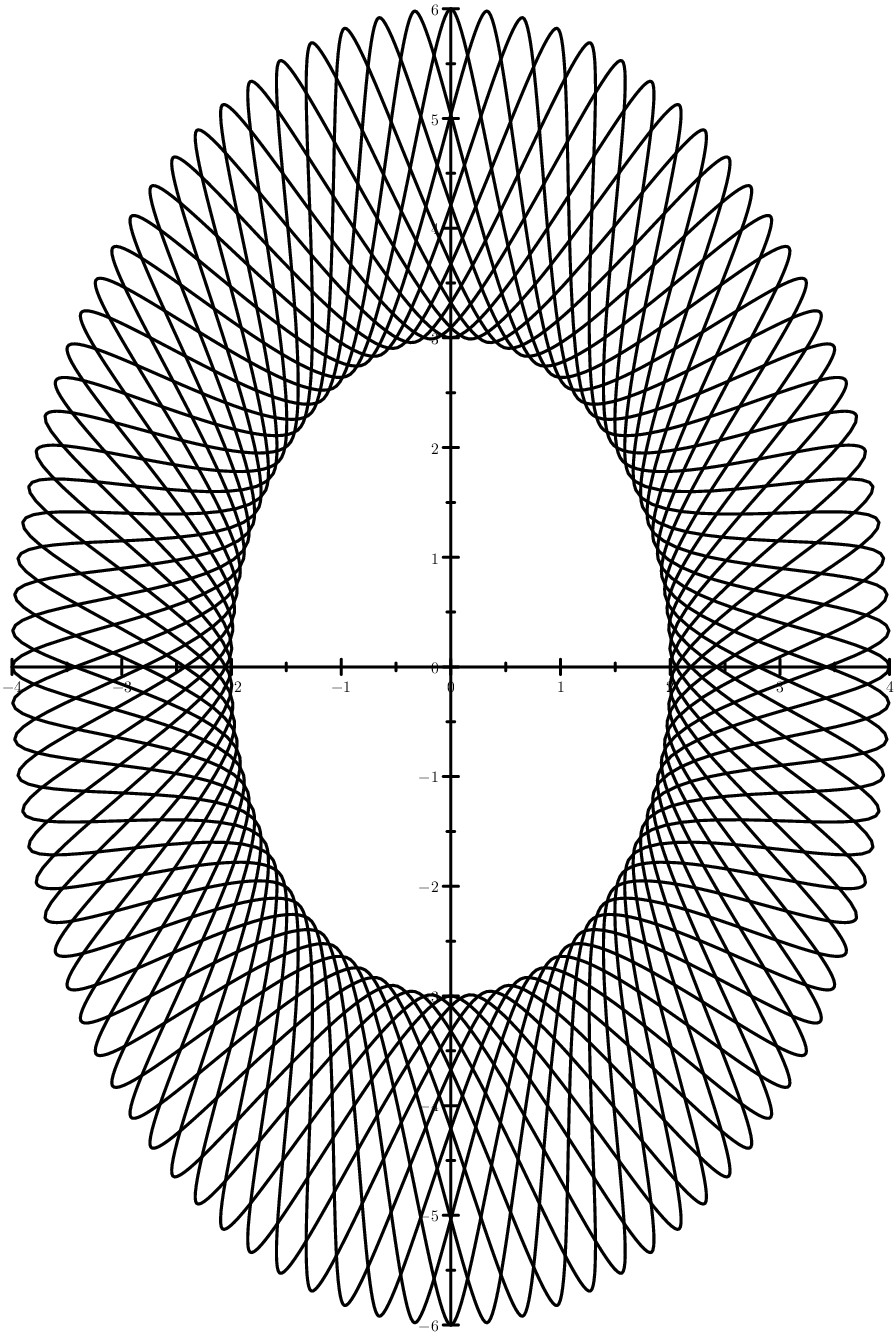Y una imagen cercana al uso industrial: guilloche, formando una especie de salida artística.
Aquí el resultado, sin embargo, no es perfecto. Primero, la función de las decenas tenía que ser ajustada para que siempre devolviera una "tensión" constante de 0.5. Y en segundo lugar, las curvas no son muy simétricas, y en la parte izquierda cerca del eje X están de alguna manera confundidas. Por supuesto, todo esto puede corregirse a mano, especialmente si hace billetes para el estado y tiene artistas muy calificados, pero puede intentar aumentar la precisión de los cálculos, porque obviamente se desvían en algunos puntos donde la curvatura de la envolvente cambia bruscamente.Como los guilloches están interpolados, surge la pregunta: ¿coinciden con, por así decirlo, "reales", es decir, dibujados por puntos. Al ser nuevo en la geometría diferencial, me resulta difícil decirlo, sino más bien "no" que "sí".¿Pero quién realmente ve la diferencia?Y el beneficio práctico es innegable: con un par de docenas de curvas Bezier, trabajar es mucho más fácil que con mil puntos, y abren muchas más posibilidades de diseño.Además, este algoritmo también se puede mejorar. Se sugieren inmediatamente dos opciones:a) especificar un número diferente de puntos en la curva externa e interna, luego no se creará el efecto de rectificar el patrón más cerca del centro, como en los ejemplos con un círculo y una elipse.b) coloque los puntos en los sobres no de manera uniforme, sino, por ejemplo, haciéndolos con más frecuencia, con menos frecuencia, lo que agregará una nueva dimensión al patrón.