🧟 🤷🏾 🙁 A qué prestamos atención al calcular la significación estadística de la prueba A / B ☺️ 😟 🥈

En Uchi.ru intentamos implementar incluso pequeñas mejoras con la prueba A / B, hubo más de 250 de ellas durante este año académico. La prueba A / B es una poderosa herramienta de prueba de cambio, sin la cual es difícil imaginar el desarrollo normal de un producto de Internet. Al mismo tiempo, a pesar de la aparente simplicidad, se pueden cometer errores graves durante la prueba A / B tanto en la etapa de diseño del experimento como en el resumen de los resultados. En este artículo hablaré sobre algunos de los aspectos técnicos de la prueba: cómo determinamos el período de prueba, resumimos y cómo evitar resultados erróneos cuando las pruebas se completan antes de lo programado y cuando se prueban varias hipótesis a la vez.

Un esquema de prueba A / B típico para nosotros (y para muchos) se ve así:

Estamos desarrollando una función, pero antes de lanzarla a toda la audiencia, queremos asegurarnos de que mejore la métrica objetivo, por ejemplo, el compromiso.
Determinamos el período durante el cual se inicia la prueba.
Dividimos aleatoriamente a los usuarios en dos grupos.
Le mostramos a un grupo la versión del producto con características (grupo experimental), el otro, el anterior (control).
En el proceso, monitoreamos la métrica para detener una prueba particularmente fallida a tiempo.
Una vez que finaliza la prueba, comparamos la métrica en los grupos experimental y de control.
Si la métrica en el grupo experimental es estadísticamente significativamente mejor que en el grupo de control, implementamos la característica probada. Si no hay significación estadística, finalizamos la prueba con un resultado negativo.

Todo parece lógico y simple, el diablo, como siempre, en los detalles.

Significación estadística, criterios y errores.

Hay un elemento de aleatoriedad en cualquier prueba A / B: las métricas de grupo dependen no solo de su funcionalidad, sino también de lo que los usuarios obtuvieron y cómo se comportan. Para sacar conclusiones confiables sobre la superioridad de un grupo, debe recopilar suficientes observaciones en la prueba, pero aun así no es inmune a los errores. Se distinguen por dos tipos:

Un error del primer tipo ocurre si arreglamos la diferencia entre los grupos, aunque en realidad no existe. El texto también contendrá un término equivalente: un resultado falso positivo. El artículo está dedicado a esos errores.
Un error del segundo tipo ocurre si arreglamos la ausencia de una diferencia, aunque de hecho lo es.

Con una gran cantidad de experimentos, es importante que la probabilidad de un error del primer tipo sea pequeña. Se puede controlar utilizando métodos estadísticos. Por ejemplo, queremos que la probabilidad de un error del primer tipo en cada experimento no exceda el 5% (este es solo un valor conveniente, puede tomar otro para sus propias necesidades). Luego haremos experimentos a un nivel de significancia de 0.05:

Hay una prueba A / B con el grupo de control A y el grupo experimental B. El objetivo es verificar que el grupo B difiera del grupo A en alguna métrica.
Formulamos la hipótesis estadística nula: los grupos A y B no difieren, y las diferencias observadas se explican por el ruido. Por defecto, siempre pensamos que no hay diferencia hasta que se demuestre lo contrario.
Verificamos la hipótesis con una regla matemática estricta: un criterio estadístico, por ejemplo, el criterio del alumno.
Como resultado, obtenemos el valor p. Se encuentra en el rango de 0 a 1 y significa la probabilidad de ver la diferencia actual o más extrema entre los grupos, siempre que la hipótesis nula sea verdadera, es decir, en ausencia de una diferencia entre los grupos.
El valor p se compara con un nivel de significancia de 0.05. Si es más grande, aceptamos la hipótesis nula de que no hay diferencias, de lo contrario creemos que existe una diferencia estadísticamente significativa entre los grupos.

Una hipótesis puede ser probada con un criterio paramétrico o no paramétrico. Los paramétricos dependen de los parámetros de distribución de la muestra de una variable aleatoria y tienen más potencia (cometen errores del segundo tipo con menos frecuencia), pero imponen requisitos sobre la distribución de la variable aleatoria en estudio.

La prueba paramétrica más común es la prueba de Student. Para dos muestras independientes (caso de prueba A / B), a veces se le llama criterio de Welch. Este criterio funciona correctamente si las cantidades estudiadas se distribuyen normalmente. Puede parecer que en datos reales este requisito casi nunca se cumple, pero de hecho la prueba requiere una distribución normal de los promedios de muestra, no las muestras en sí. En la práctica, esto significa que el criterio se puede aplicar si tiene muchas observaciones en su prueba (decenas a cientos) y no hay colas muy largas en las distribuciones. La naturaleza de la distribución de las observaciones iniciales no es importante. El lector puede verificar independientemente que el criterio de Alumno funcione correctamente incluso en muestras generadas a partir de Bernoulli o distribuciones exponenciales.

De los criterios no paramétricos, el criterio de Mann-Whitney es popular. Debe usarse si sus muestras son muy pequeñas o tienen valores atípicos grandes (el método compara las medianas, por lo tanto, es resistente a los valores atípicos). Además, para que el criterio funcione correctamente, las muestras deben tener pocos valores coincidentes. En la práctica, nunca tuvimos que aplicar criterios no paramétricos, en nuestras pruebas siempre usamos el criterio del estudiante.

El problema de la prueba de hipótesis múltiples

El problema más obvio y más simple: si en la prueba hay varios grupos experimentales además del grupo de control, resumir los resultados con un nivel de significancia de 0.05 conducirá a un aumento múltiple en la proporción de errores del primer tipo. Esto se debe a que, con cada aplicación del criterio estadístico, la probabilidad de un error del primer tipo será del 5%. Con el número de grupos

n g r o u p s

$ngroups$ y nivel de significancia

α

$\alpha$ La probabilidad de que algún grupo experimental gane por casualidad es:

P (a n y f a l s e p o s i t i v e) = 1 - (1 - α)^{n g r o u p s}

$P(any\ false\ positive) = 1 − (1 − \alpha) ^ {ngroups}$

Por ejemplo, para los tres grupos experimentales obtenemos el 14.3% en lugar del esperado 5%. El problema se resuelve con la corrección de Bonferroni para la prueba de hipótesis múltiples: solo necesita dividir el nivel de significancia por el número de comparaciones (es decir, grupos) y trabajar con él. Para el ejemplo anterior, el nivel de significancia, teniendo en cuenta la enmienda, será 0.05 / 3 = 0.0167 y la probabilidad de al menos un error del primer tipo será aceptable 4.9%.

Método Hill - Bonferroni

— , , , .

n g r o u p s

$ngroups$ p-value ,

s t e p_n u m b e r

$step\_number$ :

α_{s t e p} = \frac{α}{n g r o u p s - s t e p_n u m b e r + 1}

$\alpha_{step} = \frac {\alpha} {ngroups − step\_number + 1}$

P-value

α / n g r o u p s

$\alpha/ngroups$ . , p-value

α / (n g r o u p s - 1)

$\alpha/(ngroups − 1)$ , . - , . ( , ) p-value, . A/B- — , — .

Estrictamente hablando, las comparaciones de grupos por diferentes métricas o secciones de la audiencia también están sujetas al problema de las pruebas múltiples. Formalmente, es bastante difícil tener en cuenta todos los controles, porque su número es difícil de predecir de antemano y, a veces, no son independientes (especialmente cuando se trata de diferentes métricas, no cortes). No existe una receta universal, confíe en el sentido común y recuerde que si verifica muchas rebanadas con diferentes métricas, en cualquier prueba puede ver un resultado estadísticamente significativo. Por lo tanto, se debe tener cuidado, por ejemplo, con el aumento significativo en la retención del quinto día de nuevos usuarios móviles de las grandes ciudades.

Problema de espionaje

Un caso particular de prueba de hipótesis múltiples es el problema de espionaje. El punto es que el valor p durante la prueba puede caer accidentalmente por debajo del nivel de significancia aceptado. Si monitorea cuidadosamente el experimento, puede captar este momento y cometer un error sobre la significación estadística.

Supongamos que nos alejamos de la configuración de la prueba que se describe al comienzo de la publicación y decidimos hacer un inventario a un nivel significativo del 5% todos los días (o solo más de una vez durante la prueba). En resumen, entiendo que la prueba es positiva si el valor p está por debajo de 0.05, y su continuación de lo contrario. Con esta estrategia, la proporción de resultados falsos positivos será proporcional al número de controles y en el primer mes alcanzará el 28%. Tal gran diferencia parece contradictoria, por lo tanto, recurrimos a la metodología de las pruebas A / A, que es indispensable para el desarrollo de esquemas de prueba A / B.

La idea de una prueba A / A es simple: simular muchas pruebas A / B en datos aleatorios con agrupación aleatoria. Obviamente no hay diferencia entre los grupos, por lo que puede estimar con precisión la proporción de errores del primer tipo en su esquema de prueba A / B. El siguiente gif muestra cómo cambia el valor p por día para cuatro de estas pruebas. Un nivel de significancia igual a 0.05 se indica mediante una línea discontinua. Cuando el valor p cae por debajo, coloreamos el gráfico de prueba en rojo. Si en este momento se resumieran los resultados de la prueba, se consideraría exitoso.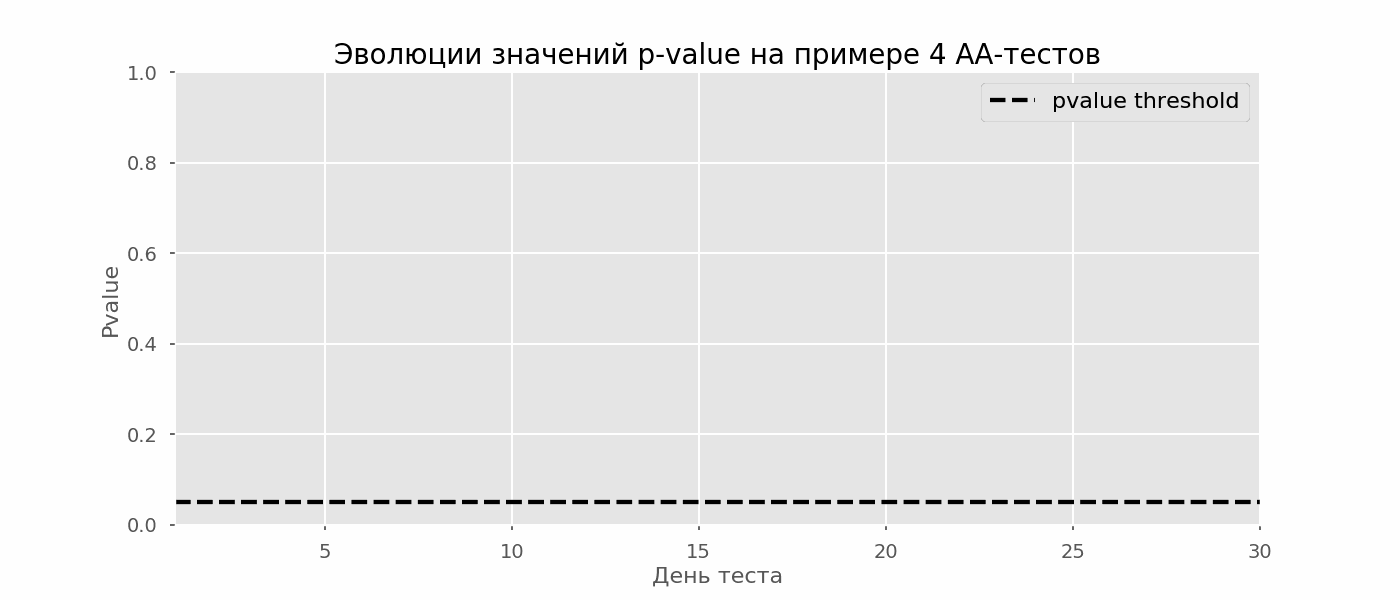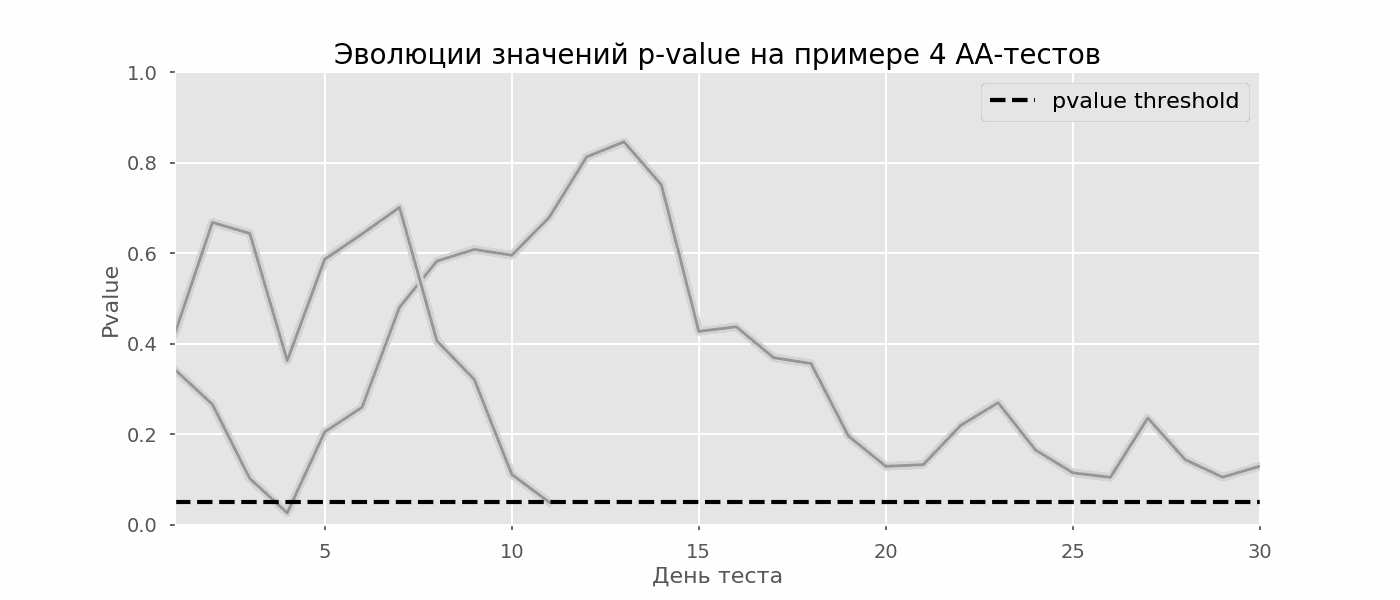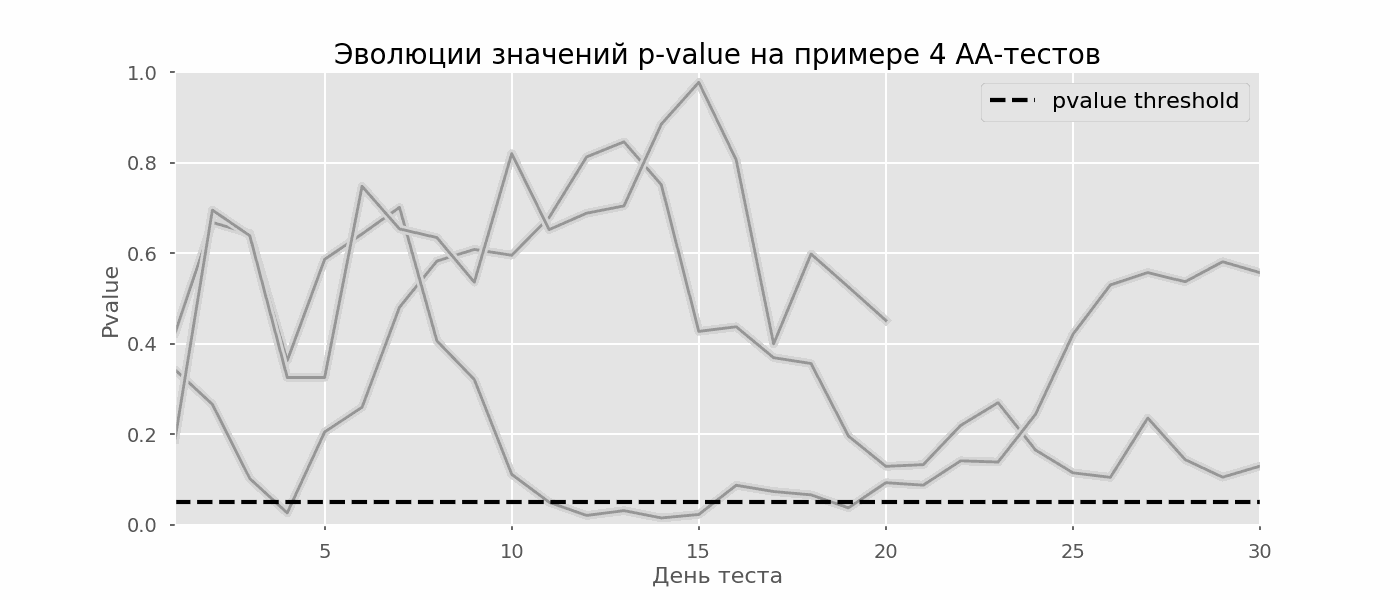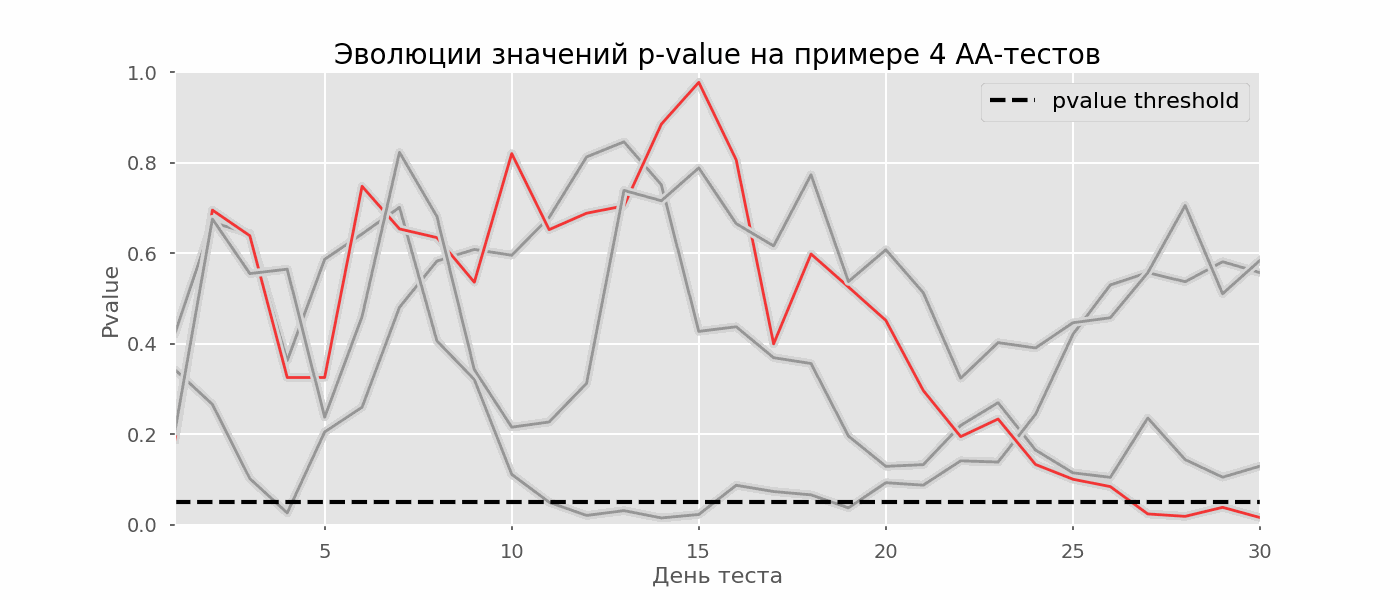

Del mismo modo, calculamos 10 mil pruebas A / A que duran un mes y comparamos las fracciones de resultados falsos positivos en el esquema con la suma al final del término y todos los días. Para mayor claridad, aquí están los horarios errantes de valor p por día para las primeras 100 simulaciones. Cada línea es el valor p de una prueba, las trayectorias de las pruebas se resaltan en rojo, que, como resultado, se consideran erróneamente exitosas (cuanto menos, mejor), la línea de puntos es el valor p requerido para reconocer la prueba como exitosa.

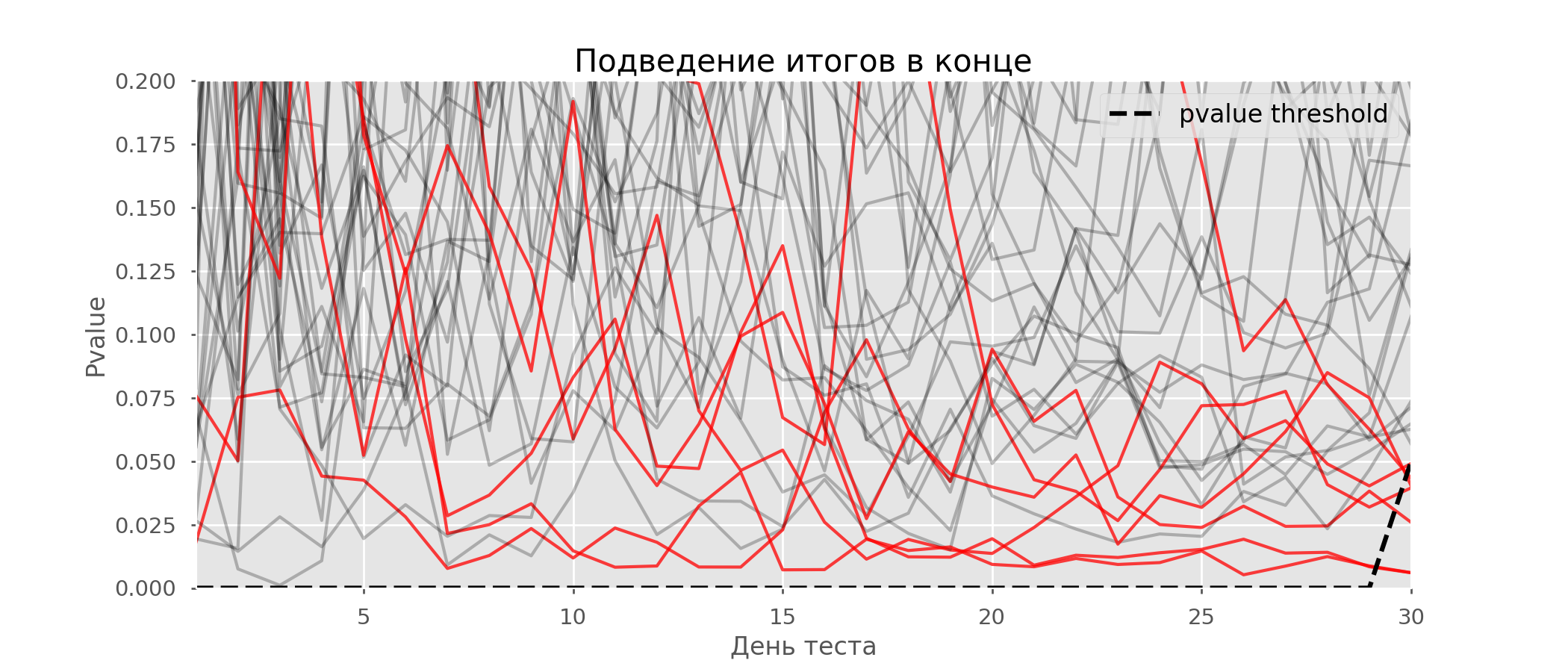En el gráfico, puede contar 7 pruebas falsas positivas, y en total entre 10 mil hubo 502, o 5%. Cabe señalar que el valor p de muchas pruebas durante el curso de las observaciones cayó por debajo de 0.05, pero al final de las observaciones fue más allá del nivel de significancia. Ahora vamos a evaluar el esquema de prueba con un informe todos los días:

Hay tantas líneas rojas que nada está claro. Redibujaremos rompiendo las líneas de prueba tan pronto como su valor p alcance un valor crítico: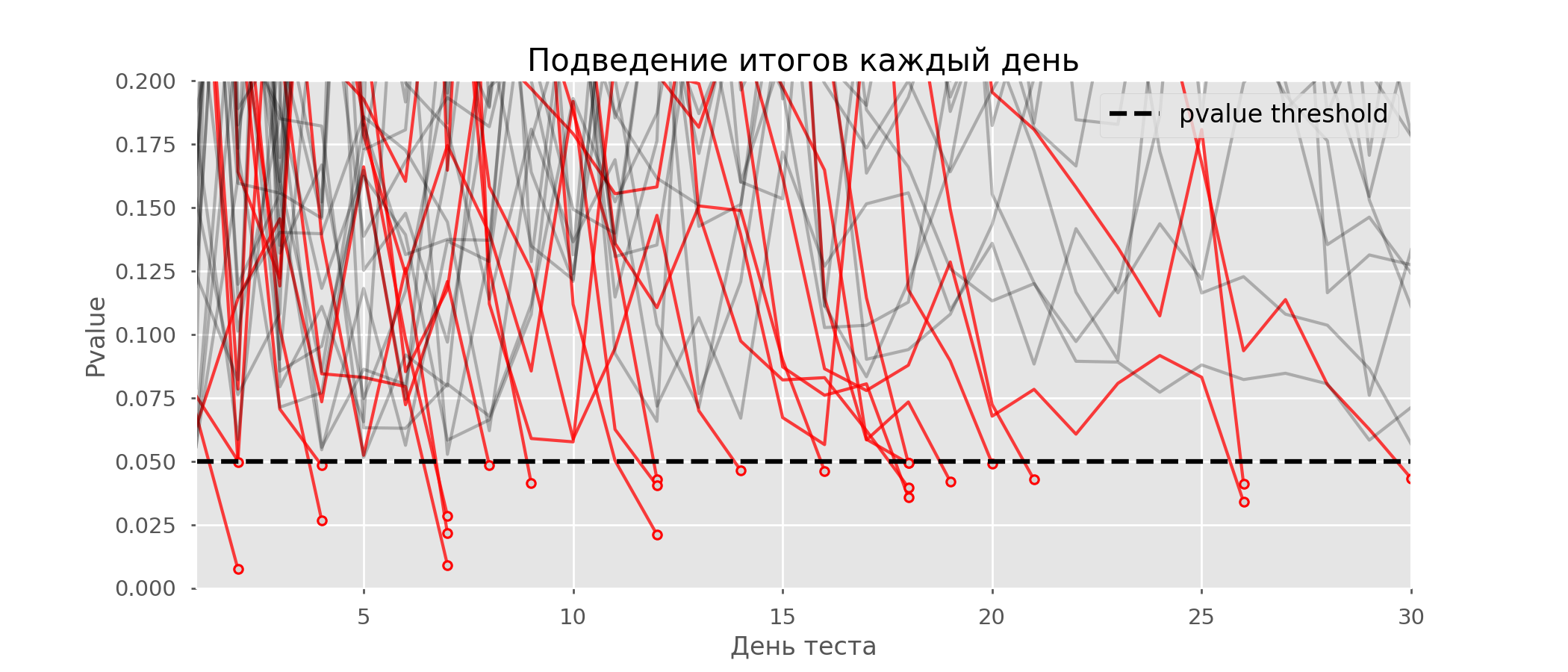

Habrá un total de 2813 pruebas de falsos positivos de 10 mil, o 28%. Está claro que tal esquema no es viable.

Aunque el problema de espiar es un caso especial de pruebas múltiples, no vale la pena aplicar correcciones estándar (Bonferroni y otras) porque resultarán demasiado conservadoras. El siguiente gráfico muestra el porcentaje de resultados falsos positivos según la cantidad de grupos probados (línea roja) y la cantidad de píos (línea verde).

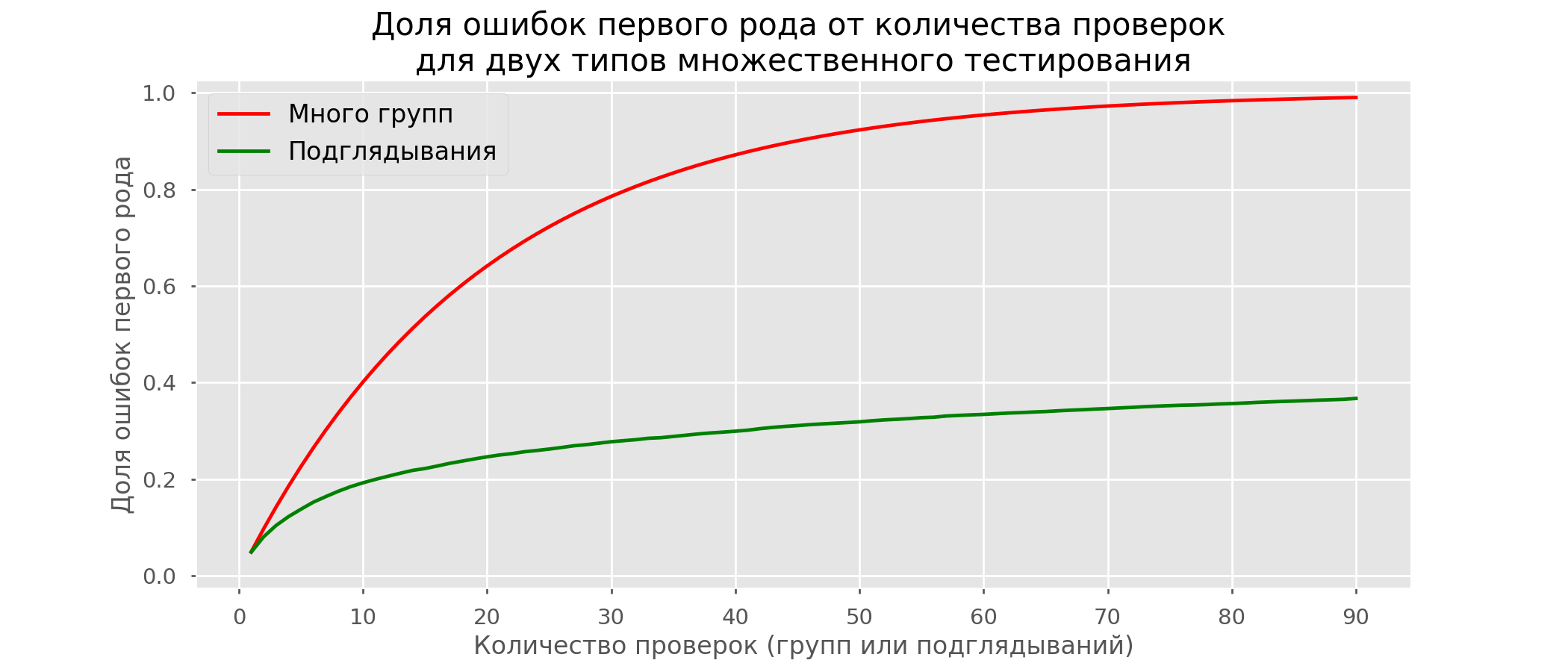Aunque en el infinito y al mirar nos acercamos a 1, la proporción de errores crece mucho más lentamente. Esto se debe a que las comparaciones en este caso ya no son independientes.

Enfoque bayesiano y el problema de espiar

, A/B- . , . .

Métodos de prueba temprana

Hay opciones de prueba que le permiten tomar la prueba prematuramente. Hablaré de dos de ellos: con un nivel constante de significancia (corrección de Pocock) y dependiente del número de píos (corrección de O'Brien-Fleming). Estrictamente hablando, para ambas correcciones necesita saber de antemano el período máximo de prueba y el número de verificaciones entre el inicio y el final de la prueba. Además, las comprobaciones deben realizarse a intervalos de tiempo aproximadamente iguales (o en cantidades iguales de observaciones).

Pocock

El método es que resumimos los resultados de las pruebas todos los días, pero con un nivel de significación reducido (más estricto). Por ejemplo, si sabemos que no haremos más de 30 verificaciones, entonces el nivel de significancia debe establecerse igual a 0.006 (seleccionado dependiendo del número de píos usando el método Monte Carlo, es decir, empíricamente). En nuestra simulación, obtenemos resultados falsos positivos del 4%; aparentemente, el umbral podría aumentarse.

A pesar de la aparente ingenuidad, algunas grandes empresas utilizan este método en particular. Es muy simple y confiable si toma decisiones sobre métricas confidenciales y sobre mucho tráfico. Por ejemplo, en Avito, por defecto , el nivel de significancia se establece en 0.005 .

O'Brien-Fleming

En este método, el nivel de significancia varía según el número de verificación. Es necesario determinar de antemano el número de pasos (o píos) en la prueba y calcular el nivel de significación para cada uno de ellos. Cuanto antes intentemos completar la prueba, más estrictos se aplicarán los criterios. Umbrales de estadísticas estudiantiles

Z_{s t e p}

$Z_{step}$ (incluido el valor en el último paso

Z_{l a s t_s t e p}

$Z_{last\_step}$ ) correspondiente al nivel de significación deseado depende del número de verificación

s t e p_n u m b e r

$step\_number$ (toma valores de 1 al número total de cheques

t o t a l_s t e p s

$total\_steps$ inclusive) y se calculan de acuerdo con la fórmula obtenida empíricamente:

Z_{l a s t_s t e p} = 2.2471 + \frac{0.3373}{t o t a l_s t e p s} - \frac{0.6331}{\sqrt{t o t a l_s t e p s}} Z_{s t e p} = Z_{l a s t_s t e p} \sqrt{\frac{t o t a l_s t e p s}{s t e p_n u m b e r}}

$Z_{last\_step} = 2.2471 + \frac {0.3373} {total\_steps} − \frac {0.6331} {\sqrt {total\_steps}} \\ Z_{step} = Z_{last\_step} \ {\sqrt { \frac {total\_steps} {step\_number}}}$

Código de probabilidades

from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score
import matplotlib.pyplot as plt

# datapoints from https://www.aarondefazio.com/tangentially/?p=83
total_steps = [
    2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60
]
last_z = [
    1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081, 
    2.107, 2.123, 2.134, 2.143, 2.164, 2.17
]
features = [
    [1/t, 1/t**0.5] for t in total_steps
]
lr = LinearRegression()
lr.fit(features, last_z)
print(lr.coef_)  # [ 0.33729346, -0.63307934]
print(lr.intercept_)  # 2.247105015502784
print(explained_variance_score(lr.predict(features), last_z))  # 0.999894

total_steps_extended = np.arange(2, 80)
features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ]
plt.plot(total_steps_extended, lr.predict(features_extended))
plt.scatter(total_steps, last_z, s=30, color='black')
plt.show()

Los niveles de significancia relevantes se calculan a través del percentil.

p e r c

$perc$ Distribución estándar correspondiente al valor de las estadísticas de los estudiantes.

Z

$Z$ :

perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2

En las mismas simulaciones, se ve así:

los resultados falsos positivos fueron 501 de cada 10 mil, o el 5% esperado. Tenga en cuenta que el nivel de significación no alcanza un valor del 5%, incluso al final, ya que este 5% debe "difuminarse" en todas las comprobaciones. En la compañía, usamos esta misma corrección si ejecutamos una prueba con la posibilidad de una parada temprana. Puede leer sobre la misma y otras enmiendas aquí .

Método Optimizely

Optimizely , , . , . , . O'Brien-Fleming’a .

Calculadora de prueba A / B

Los detalles de nuestro producto son tales que la distribución de cualquier métrica varía mucho según la audiencia de la prueba (por ejemplo, el número de clase) y la época del año. Por lo tanto, no será posible aceptar las reglas para la fecha de finalización de la prueba en el espíritu de "la prueba finalizará cuando se ingresen 1 millón de usuarios en cada grupo" o "la prueba finalizará cuando el número de tareas resueltas alcance los 100 millones". Es decir, funcionará, pero en la práctica, para esto, será necesario tener en cuenta demasiados factores:

qué clases entran en el examen;
la prueba se distribuye a maestros o estudiantes;
tiempo del año académico;
prueba para todos los usuarios o solo para los nuevos.

Sin embargo, en nuestros esquemas de prueba A / B, siempre debe fijar la fecha de finalización por adelantado. Para predecir la duración de la prueba, desarrollamos una aplicación interna: calculadora de prueba A / B. En función de la actividad de los usuarios del segmento seleccionado durante el año pasado, la aplicación calcula el período durante el cual se debe ejecutar la prueba para corregir significativamente la elevación en X% por la métrica seleccionada. La corrección para múltiples pruebas también se tiene en cuenta automáticamente y los niveles de significancia umbral se calculan para una parada temprana de la prueba.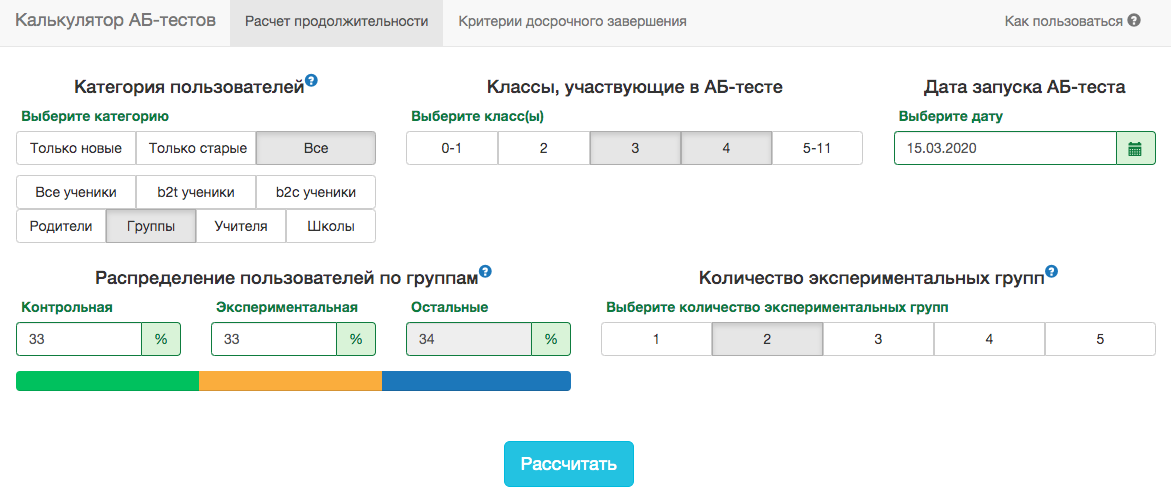

Todas las métricas se calculan al nivel de los objetos de prueba. Si la métrica es el número de problemas resueltos, entonces, en la prueba a nivel del maestro, esta será la suma de los problemas resueltos por sus alumnos. Como usamos el criterio del alumno, podemos calcular previamente los agregados que necesita la calculadora para todos los sectores posibles. Para cada día desde el comienzo de la prueba, debe saber la cantidad de personas en la prueba

u s e r s_c n t

$users\_cnt$ , el valor promedio de la métrica

m e t r i c_m e a n

$metric\_mean$ y su varianza

m e t r i c_s t d

$metric\_std$ . Arreglando las acciones del grupo de control

c o n t r o l_g r o u p_s h a r e

$control\_group\_share$ grupo experimental

e x p_g r o u p_s h a r e

$exp\_group\_share$ y ganancia esperada de la prueba

u p l i f t_e x p e c t e d

$uplift\_expected$ en porcentaje, puede calcular los valores esperados de las estadísticas de los estudiantes

t t e s t_s t a t_v a l u e

$ttest\_stat\_value$ y el valor p correspondiente para cada día de la prueba:

t t e s t_s t a t_p r e c u r s o r = \frac{m e t r i c_m e a n \sqrt{u s e r s_c n t}}{m e t r i c_s t d} t t e s t_s t a t_v a l u e = \frac{t t e s t_s t a t_p r e c u r s o r}{\sqrt{\frac{1}{c o n t r o l_g r o u p_s h a r e} + \frac{1}{e x p_g r o u p_s h a r e}}} * u p l i f t_e x p e c t e d / 100

$ttest\_stat\_precursor = \frac{metric\_mean\ \sqrt {users\_cnt}}{metric\_std} \\ ttest\_stat\_value = \frac {ttest\_stat\_precursor} {\sqrt{ \frac{1} {control\_group\_share} + \frac {1} {exp\_group\_share}}} * uplift\_expected / 100$

A continuación, es fácil obtener valores p para cada día:

pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2

Conociendo el valor p y el nivel de significancia, teniendo en cuenta todas las correcciones para cada día de la prueba, para cualquier duración de la prueba, puede calcular la elevación mínima que se puede detectar (en la literatura inglesa - MDE, efecto detectable mínimo). Después de eso, es fácil resolver el problema inverso: determinar la cantidad de días necesarios para identificar la elevación esperada.

Conclusión

En conclusión, quiero recordar los principales mensajes del artículo:

Si compara los valores promedio de la métrica en grupos, lo más probable es que el criterio de Estudiante le convenga. La excepción son tamaños de muestra extremadamente pequeños (docenas de observaciones) o distribuciones métricas anormales (en la práctica, no lo he visto).
Si hay varios grupos en la prueba, use correcciones para la prueba de hipótesis múltiples. La corrección más simple de Bonferroni servirá.
.
. .
. , , , , O'Brien-Fleming.
A/B-, A/A-.

A pesar de todo lo anterior, los negocios y el sentido común no deberían sufrir por el rigor matemático. A veces es posible implementar funcionalmente todo lo que no mostró un aumento significativo en la prueba, algunos cambios ocurren inevitablemente sin ninguna prueba. Pero si realiza cientos de pruebas al año, su análisis preciso es especialmente importante. De lo contrario, existe el riesgo de que el número de falsos positivos sea comparable a los realmente útiles.

A qué prestamos atención al calcular la significación estadística de la prueba A / B