🚃 👆🏼 🍫 3D hágalo usted mismo. Parte 2: es tridimensional 🧥 👩‍🍳 🖕

En la parte anterior, descubrimos cómo mostrar objetos bidimensionales, como un píxel y una línea (segmento), pero realmente desea crear rápidamente algo tridimensional. En este artículo, por primera vez, trataremos de mostrar un objeto 3D en la pantalla y conocer nuevos objetos matemáticos, como un vector y una matriz, así como algunas operaciones en ellos, pero solo aquellos que sean aplicables en la práctica.

En la segunda parte consideraremos:

Sistemas coordinados
Punto y vector
La matriz
Vértices e índices
Transportador de visualización

Sistemas coordinados

Vale la pena señalar que algunos ejemplos y operaciones en los artículos se presentan de manera inexacta y se simplifican enormemente para mejorar la comprensión del material, captando la esencia, puede encontrar de forma independiente la mejor solución o corregir errores e inexactitudes en el código de demostración. Antes de dibujar algo tridimensional, es importante recordar que todo lo tridimensional en la pantalla se muestra en píxeles bidimensionales. Para que los objetos dibujados por píxeles se vean tridimensionales, necesitamos hacer un poco de matemática. No consideraremos fórmulas y objetos sin ver su aplicación. Por eso, todas las operaciones matemáticas que encontrará en este artículo se pondrán en práctica, lo que simplificará su comprensión.

Lo primero que hay que entender es el sistema de coordenadas. Veamos qué sistemas de coordenadas se utilizan y también elija cuál usar para nosotros.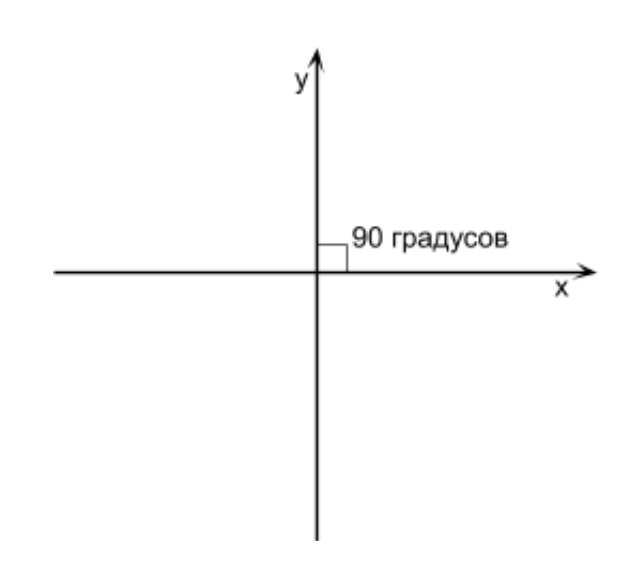

¿Qué es un sistema de coordenadas? Esta es una forma de determinar la posición de un punto o personaje en un juego que consiste en puntos que usan números. El sistema de coordenadas tiene 2 direcciones de los ejes (los designaremos como X, Y) si trabajamos con gráficos 2D. Si establecemos un objeto 2D con una Y más grande y se vuelve más alto que antes, esto significa que el eje Y está hacia arriba. Si le damos al objeto una X más grande y se vuelve más a la derecha, esto significa que el eje X se dirige hacia la derecha. Esta es la dirección de los ejes, y juntos se denominan el sistema de coordenadas. Si se forma un ángulo de 90 grados en la intersección de los ejes X e Y, dicho sistema de coordenadas se llama rectangular (también llamado sistema de coordenadas cartesianas) (vea la Figura anterior).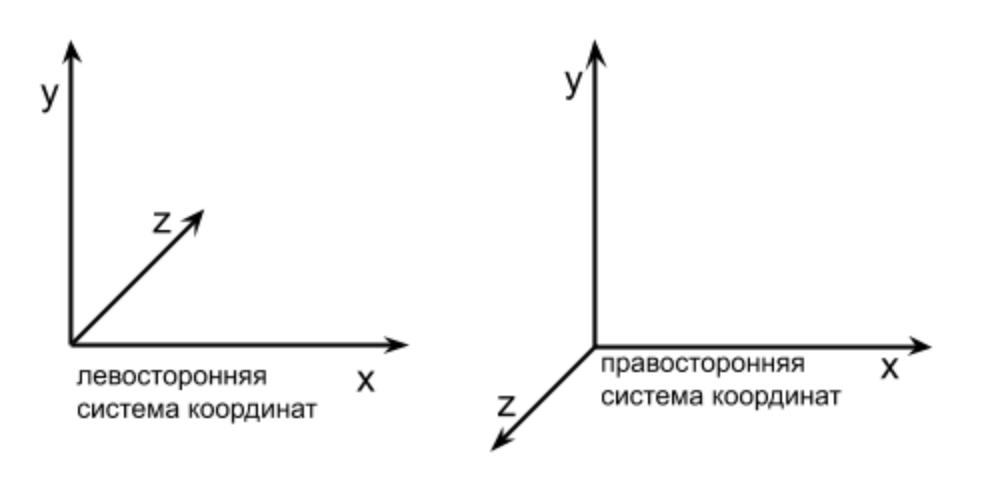

Pero era un sistema de coordenadas en el mundo 2D, en el tridimensional, aparece otro eje Z. Si el eje Y (dicen ordenadas) le permite dibujar más arriba / abajo, el eje X (también dicen las abscisas) a la izquierda / derecha, entonces el eje Z (aún say apply) le permite acercar / alejar objetos. En los gráficos tridimensionales, a menudo (pero no siempre) se usa un sistema de coordenadas en el que el eje Y se dirige hacia arriba, el eje X se dirige hacia la derecha, pero Z se puede dirigir en una dirección o en otra. Es por eso que dividiremos los sistemas de coordenadas en 2 tipos: del lado izquierdo y del lado derecho (ver. Figura anterior).

Como se puede ver en la figura, el sistema de coordenadas zurdo (también dicen que el sistema de coordenadas izquierdo) se llama cuando el eje Z se aleja de nosotros (cuanto más grande es la Z, más lejos está el objeto), si el eje Z se dirige hacia nosotros, entonces este es un sistema de coordenadas diestro (también dicen sistema de coordenadas derecho). ¿Por qué se llaman así? El izquierdo, porque si la mano izquierda se dirige con la palma hacia arriba y con los dedos hacia el eje X, el pulgar indicará la dirección Z, es decir, se dirigirá hacia el monitor, si X se dirige hacia la derecha. Haga lo mismo con su mano derecha, y el eje Z se alejará del monitor, con X a la derecha. Confundido con los dedos? En Internet hay diferentes formas de poner la mano y los dedos para obtener las direcciones necesarias de los ejes, pero esta no es una parte obligatoria.

Para trabajar con gráficos en 3D, hay muchas bibliotecas para diferentes idiomas, donde se utilizan diferentes sistemas de coordenadas. Por ejemplo, la biblioteca Direct3D usa un sistema de coordenadas para zurdos, y en OpenGL y WebGL el sistema de coordenadas para diestros, en VulkanAPI, el eje Y está hacia abajo (cuanto más pequeño es Y, más alto es el objeto) y Z es de nosotros, pero estas son solo convenciones, en las bibliotecas podemos especificar que sistema de coordenadas, que consideramos más conveniente.

¿Qué sistema de coordenadas deberíamos elegir? Cualquiera es adecuado, solo estamos aprendiendo y la dirección de los ejes ahora no afectará la asimilación del material. En los ejemplos, utilizaremos el sistema de coordenadas derecho y cuanto menos especifiquemos Z para el punto, más lejos estará de la pantalla, mientras que X, Y se dirigirá hacia la derecha / arriba.

Punto y vector

Ahora básicamente sabes qué son los sistemas de coordenadas y qué son las direcciones de los ejes. A continuación, debe analizar qué son un punto y un vector, porque los necesitaremos en este artículo para practicar. Un punto en el espacio 3D es una ubicación especificada a través de [X, Y, Z]. Por ejemplo, queremos ubicar a nuestro personaje en el origen mismo (quizás en el centro de la ventana), entonces su posición será [0, 0, 0], o podemos decir que está ubicado en el punto [0, 0, 0]. Ahora, queremos colocar al oponente a la izquierda del jugador 20 unidades (por ejemplo, píxeles), lo que significa que se ubicará en el punto [-20, 0, 0]. Trabajaremos constantemente con puntos, por lo que los analizaremos con más detalle más adelante.

¿Qué es un vector? Esta es la dirección. En el espacio 3D, se describe, como un punto, por 3 valores [X, Y, Z]. Por ejemplo, necesitamos mover el personaje 5 unidades hacia arriba cada segundo, por lo que cambiaremos Y, agregando 5 cada segundo, pero no tocaremos X y Z, este movimiento puede escribirse como un vector [0, 5, 0]. Si nuestro personaje se mueve constantemente hacia abajo en 2 unidades y hacia la derecha en 1, entonces el vector de su movimiento se verá así: [1, -2, 0]. Escribimos -2 porque Y abajo disminuye.

El vector no tiene posición y [X, Y, Z] indican la dirección. Se puede agregar un vector a un punto para obtener un nuevo punto desplazado por un vector. Por ejemplo, ya mencioné anteriormente que si queremos mover un objeto 3D (por ejemplo, un personaje del juego) cada 5 unidades hacia arriba, entonces el vector de desplazamiento será así: [0, 5, 0]. ¿Pero cómo usarlo para moverte?

Suponga que el carácter está en el punto [5, 7, 0], y el vector de desplazamiento es [0, 5, 0]. Si agregamos un vector al punto, obtenemos una nueva posición de jugador. Puede agregar un punto con un vector o un vector con un vector de acuerdo con la siguiente regla.

Un ejemplo de agregar un punto y un vector :

[ 5, 7, 0 ] + [ 0, 5, 0 ] = [ 5 + 0, 7 + 5 , 0 + 0 ] = [5, 12, 0] - esta es la nueva posición de nuestro personaje.

Como puede ver, nuestro personaje se movió 5 unidades hacia arriba, a partir de aquí aparece un nuevo concepto: la longitud del vector. Cada vector lo tiene, excepto el vector [0, 0, 0], que se llama el vector cero, dicho vector tampoco tiene dirección. Para el vector [0, 5, 0], la longitud es 5, porque dicho vector desplaza el punto 5 unidades hacia arriba. El vector [0, 0, 10] tiene una longitud de 10 porque puede cambiar el punto en 10 a lo largo del eje Z. Pero el vector [12, 3, -4] no te dice cuál es la longitud, por lo que utilizaremos la fórmula para calcular la longitud del vector. Surge la pregunta, ¿por qué necesitamos la longitud del vector? Una aplicación es averiguar qué tan lejos se moverá el personaje, o comparar las velocidades de los personajes que tienen un vector de desplazamiento más largo, eso es más rápido. La longitud también se usa para algunas operaciones en vectores.La longitud del vector se puede calcular utilizando la siguiente fórmula de la primera parte (solo se agregó Z):

L e n g t h = \sqrt{X^{2} + Y^{2} + Z^{2}}

$Length = \sqrt{X^2+Y^2+Z^2}$

Calculemos la longitud del vector usando la fórmula anterior [6, 3, -8];

L e n g t h = \sqrt{6 * 6 + 3 * 3 + - 8 * - 8} = \sqrt{36 + 9 + 64} = \sqrt{109} \approx 10.44

$Length = \sqrt{6 * 6 + 3 * 3 + -8 * -8} = \sqrt{36 + 9 + 64} = \sqrt{109} ≈ 10.44$

La longitud del vector [6, 3, -8] es aproximadamente 10.44.

Ya sabemos qué es un punto, un vector, cómo sumar un punto y un vector (o 2 vectores), y cómo calcular la longitud de un vector. Agreguemos una clase de vector e implementemos el cálculo de suma y longitud en ella. También quiero prestar atención al hecho de que no crearemos una clase para un punto, si necesitamos un punto, usaremos la clase vectorial, porque tanto el punto como el vector almacenan X, Y, Z, solo para el punto en esta posición, y para el vector la dirección.

Agregue la clase de vector al proyecto del artículo anterior, puede agregarla debajo de la clase Drawer. Llamé a Vector mi clase y le agregué 3 propiedades X, Y, Z:

class Vector {
  x = 0;
  y = 0;
  z = 0;

  constructor(x, y, z) {
    this.x = x;
    this.y = y;
    this.z = z;
  }
}

Tenga en cuenta que los campos x, y, z sin las funciones de "accesores", por lo que podemos acceder directamente a los datos en el objeto, esto se hace para un acceso más rápido. Más adelante, optimizaremos aún más este código, pero por ahora, lo dejamos para mejorar la legibilidad.

Ahora implementamos la suma de vectores. La función tomará 2 vectores sumables, así que estoy pensando en hacerlo estático. El cuerpo de la función funcionará de acuerdo con la fórmula anterior. El resultado de nuestra suma es un nuevo vector, con el que volveremos:

static add(v1, v2) {
    return new Vector(
        v1.x + v2.x,
        v1.y + v2.y,
        v1.z + v2.z,
    );
}

Queda por implementar la función de calcular la longitud del vector. Nuevamente, implementamos todo de acuerdo con las fórmulas que eran más altas:

getLength() {
    return Math.sqrt(
        this.x * this.x + this.y * this.y + this.z * this.z
    );
}

Ahora veamos otra operación en el vector, que se necesitará un poco más adelante en esto y mucho más en los artículos posteriores: "normalización del vector". Supongamos que tenemos un personaje en el juego a quien movemos con las teclas de flecha. Si presionamos hacia arriba, se mueve al vector [0, 1, 0], si está hacia abajo, entonces [0, -1, 0], a la izquierda [-1, 0, 0] y a la derecha [1, 0, 0]. Se puede ver claramente aquí que las longitudes de cada uno de los vectores son 1, es decir, la velocidad del personaje es 1. Y agreguemos un movimiento diagonal, si el jugador sujeta la flecha hacia arriba y hacia la derecha, ¿cuál será el vector de desplazamiento? La opción más obvia es el vector [1, 1, 0]. Pero si calculamos su longitud, veremos que es aproximadamente igual a 1.414. Resulta que nuestro personaje irá más rápido en diagonal? Esta opción no es adecuada, pero para que nuestro personaje vaya en diagonal a una velocidad de 1, el vector debe ser:[0,707, 0,707, 0]. ¿De dónde saqué ese vector? Tomé el vector [1, 1, 0] y lo normalicé, después de lo cual obtuve [0.707, 0.707, 0]. Es decir, la normalización es la reducción de un vector a una longitud de 1 (unidad de longitud) sin cambiar su dirección. Tenga en cuenta que los vectores [0.707, 0.707, 0] y [1, 1, 0] apuntan en la misma dirección, es decir, el personaje en ambos casos se moverá estrictamente hacia la derecha, pero el vector [0.707, 0.707, 0] está normalizado y la velocidad del personaje Ahora será igual a 1, lo que elimina el error con el movimiento diagonal acelerado. Siempre se recomienda normalizar el vector antes de cualquier cálculo para evitar varios tipos de errores. Veamos cómo normalizar un vector. Es necesario dividir cada uno de sus componentes (X, Y, Z) por su longitud. La función de encontrar la longitud ya está ahí, la mitad del trabajo está hecho,ahora escribimos la función de normalización del vector (dentro de la clase Vector):

normalize() {
    const length = this.getLength();
    
    this.x /= length;
    this.y /= length;
    this.z /= length;
    
    return this;
}

El método normalizar normaliza el vector y lo devuelve (esto), esto es necesario para que en el futuro sea posible usar normalizar en expresiones.

Ahora que sabemos qué es la normalización de un vector, y sabemos que es mejor realizarlo antes de usar el vector, surge la pregunta. Si la normalización de un vector es una reducción a la longitud de una unidad, es decir, la velocidad de movimiento de un objeto (personaje) será igual a 1, entonces, ¿cómo acelerar el personaje? Por ejemplo, al mover un personaje diagonalmente hacia arriba / derecha a una velocidad de 1, su vector será [0.707, 0.707, 0], y ¿qué vector será si queremos mover el personaje 6 veces más rápido? Para hacer esto, hay una operación llamada "multiplicar un vector por un escalar". El escalar es el número habitual por el cual se multiplica el vector. Si el escalar es igual a 6, entonces el vector se volverá 6 veces más largo, y nuestro personaje es 6 veces más rápido, respectivamente. ¿Cómo hacer la multiplicación escalar? Para esto, es necesario multiplicar cada componente del vector por un escalar. Por ejemplo, resolvemos el problema anterior,cuando un personaje que se mueve a un vector [0.707, 0.707, 0] (velocidad 1) necesita acelerarse 6 veces, es decir, multiplique el vector por el escalar 6. La fórmula para multiplicar el vector "V" por el "s" escalar es la siguiente:

V * s = [\begin{matrix} V_{x} * s & V_{y} * s & V_{z} * s \end{matrix}]

$V * s = \begin{bmatrix}V_x * s&V_y*s&V_z*s\end{bmatrix}$

En nuestro caso, será:

[\begin{matrix} 0.707 * 6 & 0.707 * 6 & 0 * 6 \end{matrix}] = [\begin{matrix} 4.242 & 4.242 & 0 \end{matrix}]

$\begin{bmatrix}0.707 * 6&0.707 * 6&0 * 6\end{bmatrix} = \begin{bmatrix}4.242&4.242&0\end{bmatrix}$ - un nuevo vector de desplazamiento cuya longitud es 6.

Es importante saber que un escalar positivo escala un vector sin cambiar su dirección; si un escalar es negativo, también escala un vector (aumenta su longitud) pero además cambia la dirección del vector al opuesto.

Implementemos la función de multiplyByScalarmultiplicar un vector por un escalar en nuestra clase Vector:

multiplyByScalar(s) {
    this.x *= s;
    this.y *= s;
    this.z *= s;
    
    return this;
}

La matriz

Descubrimos un poco los vectores y algunas operaciones sobre ellos que serán necesarios en este artículo. A continuación, debe lidiar con las matrices.

Podemos decir que una matriz es la matriz bidimensional más común. Es solo que en la programación usan el término "matriz bidimensional", y en matemáticas usan la "matriz". ¿Por qué se necesitan matrices en la programación 3D? Analizaremos esto tan pronto como aprendamos a trabajar un poco con ellos.

Utilizaremos solo matrices numéricas (una matriz de números). Cada matriz tiene su propio tamaño (como cualquier matriz bidimensional). Aquí hay algunos ejemplos de matrices:

M = [\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}]

$M=\begin{bmatrix}1&2&3\\4&5&6\end{bmatrix}$

Matriz 2 por 3

M = [\begin{matrix} 2 & 4 & 3 \\ 3 & 4 & 4 \\ 5 & - 2 & 2 \end{matrix}]

$M=\begin{bmatrix}2&4&3\\3&4&4\\5&-2&2\end{bmatrix}$

Matriz 3 por 3

M = [\begin{matrix} 2 \\ 3 \\ 0 \\ 5 \end{matrix}]

$M=\begin{bmatrix}2\\3\\0\\5\end{bmatrix}$

Matriz 4 en 1

M = [\begin{matrix} 5 & 0 & 7 \\ 2 & - 1 & 7 \\ 9 & 2 & 8 \\ 3 & 5 & 1 \end{matrix}]

$M=\begin{bmatrix}5&0&7\\2&-1&7\\9&2&8\\3&5&1\end{bmatrix}$

Matriz 4 por 3

De todas las operaciones en matrices, ahora consideramos solo la multiplicación (el resto más adelante). Resulta que la multiplicación de matrices no es la operación más fácil, puede confundir fácilmente si no sigue cuidadosamente el orden de multiplicación. Pero no te preocupes, tendrás éxito, porque aquí solo multiplicaremos y resumiremos. Para empezar, debemos recordar un par de características de multiplicación que necesitamos:

Si intentamos multiplicar el número A por el número B, entonces esto es lo mismo que B * A. Si reorganizamos los operandos y el resultado no cambia bajo ninguna acción, entonces dicen que la operación es conmutativa. Ejemplo: a + b = b + a la operación es conmutativa, a - b ≠ b - a la operación no es conmutativa, a * b = b * a la operación de multiplicar números es conmutativa. Entonces, la operación de multiplicación matricial no es conmutativa, en contraste con la multiplicación de números. Es decir, multiplicar la matriz M por la matriz N no será igual a la multiplicación de la matriz N por M.
La multiplicación de matrices es posible si el número de columnas de la primera matriz (que está a la izquierda) es igual al número de filas en la segunda matriz (que está a la derecha).

Ahora veremos la segunda característica de la multiplicación de matrices (cuando es posible la multiplicación). Aquí hay algunos ejemplos que demuestran cuándo es posible la multiplicación y cuándo no:

M_{1} = [\begin{matrix} 1 & 2 \end{matrix}]

$M_1=\begin{bmatrix}1&2\end{bmatrix}$

M_{2} = [\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}]

$M_2=\begin{bmatrix}1&2&3\\4&5&6\end{bmatrix}$

M1 M2 , .. 2 , 2 .

M_{1} = [\begin{matrix} 3 & 2 & 5 \\ 4 & 4 & 2 \\ - 7 & 4 & 5 \\ 7 & 9 & 4 \end{matrix}]

$M_1=\begin{bmatrix}3&2&5\\4&4&2\\-7&4&5\\7&9&4\end{bmatrix}$

M_{2} = [\begin{matrix} 1 & 0 \\ 4 & 5 \\ 6 & - 9 \end{matrix}]

$M_2=\begin{bmatrix}1&0\\4&5\\6&-9\end{bmatrix}$

1 2 , .. 3 , 3 .

M_{1} = [\begin{matrix} 5 & 4 \\ 0 & 3 \end{matrix}]

$M_1=\begin{bmatrix}5&4\\0&3\end{bmatrix}$

M_{2} = [\begin{matrix} 7 & 3 \\ 0 & 3 \\ 6 & 3 \end{matrix}]

$M_2=\begin{bmatrix}7&3\\0&3\\6&3\end{bmatrix}$

1 2 , .. 2 , 3 .

Creo que estos ejemplos aclararon un poco la imagen cuando es posible la multiplicación. El resultado de la multiplicación de matrices siempre será una matriz, cuyo número de filas será igual al número de filas de la primera matriz, y el número de columnas es igual al número de columnas de la segunda. Por ejemplo, si multiplicamos la matriz 2 por 6 y 6 por 8, obtenemos una matriz de tamaño 2 por 8. Ahora vamos directamente a la multiplicación misma.

Para la multiplicación, es importante recordar que las columnas y filas de la matriz están numeradas a partir de 1, y en la matriz de 0. El primer índice en el elemento de la matriz indica el número de fila y el segundo el número de columna. Es decir, si el elemento de matriz (elemento de matriz) se escribe como: m28, esto significa que pasamos a la segunda fila y a la octava columna. Pero dado que trabajaremos con matrices en el código, toda la indexación de filas y columnas comenzará en 0.

Intentemos multiplicar 2 matrices A y B con tamaños y elementos específicos:

A = [\begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix}]

$A=\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}$

B = [\begin{matrix} 7 & 8 \\ 9 & 10 \end{matrix}]

$B=\begin{bmatrix}7&8\\9&10\end{bmatrix}$

Se puede ver que la matriz A tiene un tamaño de 3 por 2, y la matriz B tiene un tamaño de 2 por 2, es posible la multiplicación:

A * B = [\begin{matrix} 1 * 7 + 2 * 9 & 1 * 8 + 2 * 10 \\ 3 * 7 + 4 * 9 & 3 * 8 + 4 * 10 \\ 5 * 7 + 6 * 9 & 5 * 8 + 6 * 10 \end{matrix}] = [\begin{matrix} 25 & 28 \\ 57 & 64 \\ 89 & 100 \end{matrix}]

$A*B=\begin{bmatrix}1*7+2*9&1*8+2*10\\3*7+4*9&3*8+4*10\\5*7+6*9&5*8+6*10\end{bmatrix}=\begin{bmatrix}25&28\\57&64\\89&100\end{bmatrix}$

Como puede ver, tenemos una matriz de 3 por 2, la multiplicación es inicialmente confusa, pero si hay una meta para aprender a multiplicar “sin estrés”, se deben resolver varios ejemplos. Aquí hay otro ejemplo de multiplicar las matrices A y B:

A = [\begin{matrix} 3 & 2 \end{matrix}]

$A=\begin{bmatrix}3&2\end{bmatrix}$

B = [\begin{matrix} 2 & - 3 & 0 \\ 1 & 4 & - 2 \end{matrix}]

$B=\begin{bmatrix}2&-3&0\\1&4&-2\end{bmatrix}$

A * B = [\begin{matrix} 3 * 2 + 2 * 1 & 3 * - 3 + 2 * 4 & 3 * 0 + 2 * - 2 \end{matrix}] = [\begin{matrix} 8 & - 1 & - 4 \end{matrix}]

$A*B=\begin{bmatrix}3*2+2*1&3*-3+2*4&3*0+2*-2\end{bmatrix}=\begin{bmatrix}8&-1&-4\end{bmatrix}$

Si la multiplicación no está completamente clara, entonces está bien, porque no tenemos que multiplicar por hoja. Escribiremos una vez la función de multiplicación de matrices y la usaremos. En general, todas estas funciones ya están escritas, pero hacemos todo por nuestra cuenta.

Ahora, algunos términos más que se utilizarán en el futuro:

Una matriz cuadrada es una matriz en la cual el número de filas es igual al número de columnas, aquí hay un ejemplo de matrices cuadradas:

[\begin{matrix} 2 & 3 \\ 6 & 4 \end{matrix}]

$\begin{bmatrix}2&3\\6&4\end{bmatrix}$

Matriz cuadrada de 2 por 2

[\begin{matrix} 5 & 6 & 7 \\ 9 & 0 & - 2 \\ 4 & 5 & 1 \end{matrix}]

$\begin{bmatrix}5&6&7\\9&0&-2\\4&5&1\end{bmatrix}$

Matriz cuadrada de 3 por 3

[\begin{matrix} 5 & 6 & 7 & 3 \\ 9 & 0 & 2 & 1 \\ 4 & 5 & 1 & 3 \\ 1 & 7 & 9 & 8 \end{matrix}]

$\begin{bmatrix}5&6&7&3\\9&0&2&1\\4&5&1&3\\1&7&9&8\end{bmatrix}$

Matriz cuadrada de 4 por 4

La diagonal principal de una matriz cuadrada se llama todos los elementos de la matriz cuyo número de fila es igual al número de columna. Ejemplos de diagonales (en este ejemplo, la diagonal principal está llena de nueves):

[\begin{matrix} 9 & 3 \\ 3 & 9 \end{matrix}]

$\begin{bmatrix}9&3\\3&9\end{bmatrix}$

[\begin{matrix} 9 & 3 & 3 \\ 3 & 9 & 3 \\ 3 & 3 & 9 \end{matrix}]

$\begin{bmatrix}9&3&3\\3&9&3\\3&3&9\end{bmatrix}$

[\begin{matrix} 9 & 3 & 3 & 3 \\ 3 & 9 & 3 & 3 \\ 3 & 3 & 9 & 3 \\ 3 & 3 & 3 & 9 \end{matrix}]

$\begin{bmatrix}9&3&3&3\\3&9&3&3\\3&3&9&3\\3&3&3&9\end{bmatrix}$

Una matriz unitaria es una matriz cuadrada en la que todos los elementos de la diagonal principal son 1 y todos los demás son 0. Ejemplos de matrices unitarias:

[\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}]

$\begin{bmatrix}1&0\\0&1\end{bmatrix}$

[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}]

$\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$

[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}$

También es importante recordar esta propiedad de que si multiplicamos cualquier matriz M por una matriz unitaria que sea adecuada en tamaño, por ejemplo, llámela I, obtenemos la matriz original M, por ejemplo: M * I = M o I * M = M. Es decir, multiplicar la matriz por la matriz de identidad no afecta el resultado. Volveremos a la matriz de identidad más tarde. En la programación 3D, a menudo usaremos una matriz cuadrada de 4 por 4.

Ahora echemos un vistazo a por qué necesitaremos matrices y por qué multiplicarlas. En la programación 3D, hay muchas matrices diferentes de 4 por 4 que, si se multiplican por un vector o punto, realizarán las acciones que necesitamos. Por ejemplo, necesitamos rotar el personaje en un espacio tridimensional alrededor del eje X, ¿cómo hacer esto? Multiplique el vector por una matriz especial, que es responsable de la rotación alrededor del eje X. Si necesita mover y rotar un punto alrededor del origen, entonces debe multiplicar este punto por una matriz especial. Las matrices tienen una propiedad excelente: combinan transformaciones (lo consideraremos en este artículo). Supongamos que necesitamos un personaje que consista en 100 puntos (vértices, pero esto también será un poco más bajo) en la aplicación, aumente 5 veces, luego gire 90 grados X, luego muévalo 30 unidades hacia arriba.Como ya se mencionó, para diferentes acciones ya hay matrices especiales que consideraremos. Para realizar la tarea anterior, por ejemplo, recorremos los 100 puntos y cada uno multiplicamos por la primera matriz para aumentar el carácter, luego multiplicamos por la segunda matriz para rotar 90 grados en X, luego multiplicamos por 3 th para mover 30 unidades hacia arriba. En total, para cada punto tenemos 3 multiplicaciones matriciales y 100 puntos, lo que significa que habrá 300 multiplicaciones, pero si tomamos y multiplicamos las matrices entre nosotros para aumentar 5 veces, giramos 90 grados a lo largo de X y nos movemos 30 unidades. arriba, obtenemos una matriz que contiene todas estas acciones. Multiplicando un punto por dicha matriz, el punto estará donde se necesita. Ahora calculemos cuántas acciones se realizan: 2 multiplicaciones por 3 matrices y 100 multiplicaciones por 100 puntos,un total de 102 multiplicaciones es definitivamente mejor que 300 multiplicaciones antes de eso. El momento en que multiplicamos 3 matrices para combinar diferentes acciones en una matriz, se llama una combinación de transformaciones y ciertamente lo haremos con un ejemplo.

Examinamos cómo multiplicar la matriz por la matriz, pero el párrafo leído anteriormente habla de la multiplicación de la matriz por un punto o vector. Para multiplicar un punto o vector, es suficiente representarlos como una matriz.

Por ejemplo, tenemos un vector [10, 2, 5] y hay una matriz:

[\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}]

$\begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix}$

Se puede ver que el vector puede ser representado por una matriz de 1 por 3 o por una matriz de 3 por 1. Por lo tanto, podemos multiplicar el vector por una matriz de 2 formas:

[\begin{matrix} 10 & 2 & 5 \end{matrix}] * [\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}]

$\begin{bmatrix}10&2&5\end{bmatrix} * \begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix}$

Aquí presentamos el vector como una matriz de 1 por 3 (también dicen un vector de fila). Tal multiplicación es posible, porque la primera matriz (vector de fila) tiene 3 columnas y la segunda matriz tiene 3 filas.

[\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}] * [\begin{matrix} 10 \\ 2 \\ 5 \end{matrix}]

$\begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix} * \begin{bmatrix}10\\2\\5\end{bmatrix}$

Aquí presentamos el vector como una matriz de 3 por 1 (también dicen un vector de columna). Tal multiplicación es posible, porque en la primera matriz hay 3 columnas, y en la segunda (vector de columna) 3 filas.

Como puede ver, podemos representar el vector como un vector de fila y multiplicarlo por una matriz, o representar el vector como un vector de columna y multiplicar la matriz por él. Verifiquemos si el resultado de la multiplicación será el mismo en ambos casos:

Multiplique el vector de fila por la matriz:

[\begin{matrix} 10 & 2 & 5 \end{matrix}] * [\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}] =

$\begin{bmatrix}10&2&5\end{bmatrix} * \begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix} =$

= [\begin{matrix} 10 * 1 + 2 * 2 + 5 * 0 & 10 * 2 + 2 * 2 + 5 * 4 & 10 * 1 + 2 * 1 + 5 * 3 \end{matrix}] = [\begin{matrix} 14 & 44 & 27 \end{matrix}]

$= \begin{bmatrix}10*1+2*2+5*0&10*2+2*2+5*4&10*1+2*1+5*3\end{bmatrix} = \begin{bmatrix}14&44&27\end{bmatrix}$

Ahora, multiplique la matriz por el vector de columna:

[\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}] * [\begin{matrix} 10 \\ 2 \\ 5 \end{matrix}] = [\begin{matrix} 1 * 10 + 2 * 5 + 1 * 5 \\ 2 * 10 + 2 * 2 + 1 * 5 \\ 0 * 10 + 4 * 2 + 3 * 5 \end{matrix}] = [\begin{matrix} 19 \\ 29 \\ 23 \end{matrix}]

$\begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix} * \begin{bmatrix}10\\2\\5\end{bmatrix}=\begin{bmatrix}1*10+2*5+1*5\\2*10+2*2+1*5\\0*10+4*2+3*5\end{bmatrix}=\begin{bmatrix}19\\29\\23\end{bmatrix}$

Vemos que multiplicando el vector fila por la matriz y la matriz por el vector columna, obtuvimos resultados completamente diferentes (recordamos la conmutatividad). Por lo tanto, en la programación 3D, hay matrices que están diseñadas para multiplicarse solo por un vector de fila, o solo por un vector de columna. Si multiplicamos la matriz prevista para el vector fila por el vector columna, obtenemos un resultado que no nos dará nada. Use la representación de vector / punto conveniente para usted (fila o columna), solo en el futuro, use las matrices apropiadas para su representación de vector / punto. Direct3D, por ejemplo, utiliza una representación en cadena de vectores, y todas las matrices en Direct3D están diseñadas para multiplicar un vector de fila por una matriz. OpenGL usa una representación de un vector (o punto) como una columna,y todas las matrices están diseñadas para multiplicar la matriz por un vector de columna. En los artículos usaremos el vector de columna y multiplicaremos la matriz por el vector de columna.

Para resumir lo que leemos sobre la matriz.

Para realizar una acción en un vector (o punto), hay matrices especiales, algunas de las cuales veremos en este artículo.
Para combinar la transformación (desplazamiento, rotación, etc.), podemos multiplicar las matrices de cada transformación entre sí y obtener una matriz que contenga todas las transformaciones juntas.
En la programación 3D, usaremos constantemente matrices de 4 por 4 cuadrados.
Podemos multiplicar la matriz por un vector (o punto) representándolo como una columna o fila. Pero para el vector de columna y el vector de fila, debe usar diferentes matrices.

Después de un pequeño análisis de las matrices, agreguemos una clase de matriz de 4 por 4 e implementemos métodos para multiplicar la matriz por la matriz y el vector por la matriz. Usaremos el tamaño de la matriz 4 por 4, porque Todas las matrices estándar que se utilizan para diversas acciones (movimiento, rotación, escala, ...) son de tal tamaño, no necesitamos matrices de un tamaño diferente.

Agreguemos la clase Matrix al proyecto. Todavía a veces la clase para trabajar con matrices de 4 por 4 se llama Matrix4, y este 4 en el título nos dice sobre el tamaño de la matriz (también dicen la matriz de 4to orden). Todos los datos de la matriz se almacenarán en una matriz bidimensional de 4 por 4.

Pasamos a la implementación de operaciones de multiplicación. No recomiendo usar bucles para esto. Para mejorar el rendimiento, todos tenemos que multiplicar línea por línea; esto sucederá debido al hecho de que todas las multiplicaciones ocurrirán con matrices de un tamaño fijo. Usaré ciclos para la operación de multiplicación, solo para guardar la cantidad de código, puede escribir toda la multiplicación sin ciclos en absoluto. Mi código de multiplicación se ve así:

class Matrix {
  static multiply(a, b) {
    const m = [
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
    ];

    for (let i = 0; i < 4; i++) {
      for (let j = 0; j < 4; j++) {
        m[i][j] = a[i][0] * b[0][j] +
          a[i][1] * b[1][j] +
          a[i][2] * b[2][j] +
          a[i][3] * b[3][j];
      }
    }

    return m;
  }
}

Como puede ver, el método toma las matrices ayb, las multiplica y devuelve el resultado en la misma matriz 4 por 4. Al comienzo del método, creé una matriz m llena de ceros, pero esto no es necesario, por lo que quería mostrar qué dimensión será el resultado, usted Puede crear una matriz de 4 por 4 sin ningún dato.

Ahora necesita implementar la multiplicación de la matriz por el vector de columna, como se discutió anteriormente. Pero si representa el vector como una columna, obtendrá una matriz de la forma:

[\begin{matrix} x \\ y \\ z \end{matrix}]

$\begin{bmatrix}x\\y\\z\end{bmatrix}$
por el cual tendremos que multiplicar por 4 por 4 matrices para realizar varias acciones. Pero en este ejemplo se ve claramente que tal multiplicación no puede realizarse, porque el vector de columna tiene 3 filas y la matriz tiene 4 columnas. ¿Qué hacer entonces? Se necesita un cuarto elemento, entonces el vector tendrá 4 filas, que será igual al número de columnas en la matriz. Agreguemos dicho cuarto parámetro al vector y llamémosle W, ahora tenemos todos los vectores 3D en forma [X, Y, Z, W] y estos vectores ya pueden multiplicarse por 4 por 4. De hecho, el componente W un propósito más profundo, pero lo conoceremos en la siguiente parte (no es por nada que tengamos una matriz de 4 por 4, no una matriz de 3 por 3). Agregue a la clase Vector, que creamos sobre el componente w. Ahora el comienzo de la clase Vector se ve así:

class Vector {
    x = 0;
    y = 0;
    z = 0;
    w = 1;

    constructor(x, y, z, w = 1) {
        this.x = x;
        this.y = y;
        this.z = z;
        this.w = w;
    }

Inicialicé W en uno, pero ¿por qué 1? Si observamos cómo se multiplican los componentes de la matriz y el vector (el ejemplo de código a continuación), puede ver que si establece W en 0 o cualquier otro valor que no sea 1, al multiplicar este W afectará el resultado, pero no sabemos cómo usarlo, y si lo hacemos 1, entonces estará en el vector, pero el resultado no cambiará de ninguna manera.

Ahora regrese a la matriz e implemente en la clase Matriz (también puede en la clase Vector, no hay diferencia) la matriz se multiplica por un vector, que ya es posible, gracias a W:

static multiplyVector(m, v) {
  return new Vector(
    m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
    m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
    m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
    m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
  )
}

Tenga en cuenta que presentamos la matriz como una matriz de 4 por 4, y el vector como un objeto con las propiedades x, y, z, w, en el futuro cambiaremos el vector y también estará representado por una matriz de 1 por 4, porque acelerará la multiplicación. Pero ahora, para ver mejor cómo se produce la multiplicación y mejorar la comprensión del código, no cambiaremos el vector.

Escribimos el código para la multiplicación de matrices entre nosotros y la multiplicación de vectores de matriz, pero aún no está claro cómo esto nos ayudará en los gráficos tridimensionales.

También quiero recordarles que llamo a un vector tanto un punto (posición en el espacio) como una dirección, porque ambos objetos contienen la misma estructura de datos x, y, z y la nueva w introducida.

Veamos algunas de las matrices que realizan operaciones básicas en vectores. La primera de estas matrices será la matriz de traducción. Multiplicando la matriz de desplazamiento por un vector (ubicación), cambiará por el número especificado de unidades en el espacio. Y aquí está la matriz de desplazamiento:

[\begin{matrix} 1 & 0 & 0 & d x \\ 0 & 1 & 0 & d y \\ 0 & 0 & 1 & d z \\ 0 & 0 & 0 & 1 \end{matrix}]

$\begin{bmatrix}1&0&0&dx\\0&1&0&dy\\0&0&1&dz\\0&0&0&1\end{bmatrix}$

Donde dx, dy, dz desplazamientos medios a lo largo de los ejes x, y, z, respectivamente, esta matriz está diseñada para multiplicarse por un vector de columna. Tales matrices se pueden encontrar en Internet o en cualquier literatura sobre programación 3D, no necesitamos crearlas nosotros mismos, tómalas ahora, como las fórmulas que usas en la escuela que solo necesitas saber o entender por qué usarlas. Verifiquemos si, de hecho, multiplicando dicha matriz por un vector, se producirá un desplazamiento. Tomemos como vector que vamos a mover el vector [10, 10, 10, 1] (siempre dejamos el 4º parámetro W siempre 1), supongamos que esta es la posición de nuestro personaje en el juego y queremos cambiarlo 10 unidades hacia arriba, 5 unidades a la derecha, y 1 unidad lejos de la pantalla. Entonces el vector de desplazamiento será así [10, 5, -1] (-1 porque tenemos un sistema de coordenadas a la derecha y el Z adicional,cuanto más pequeño es). Si calculamos el resultado sin matrices, por la suma usual de vectores. Eso dará como resultado el siguiente resultado: [10 + 10, 10 + 5, 10 + -1, 1] = [20, 15, 9, 1]: estas son las nuevas coordenadas de nuestro personaje. Multiplicando la matriz anterior por las coordenadas iniciales [10, 10, 10, 1], deberíamos obtener el mismo resultado, verifiquemos esto en el código, escriba la multiplicación después de las clases Drawer, Vector y Matrix:

const translationMatrix = [
  [1, 0, 0, 10],
  [0, 1, 0, 5],
  [0, 0, 1, -1],
  [0, 0, 0, 1],
]
        
const characterPosition = new Vector(10, 10, 10)
        
const newCharacterPosition = Matrix.multiplyVector(
  translationMatrix, characterPosition
)
console.log(newCharacterPosition)

En este ejemplo, sustituimos el desplazamiento de caracteres deseado (translationMatrix) en la matriz de desplazamiento, inicializamos su posición inicial (characterPosition) y luego lo multiplicamos con la matriz, y el resultado se obtuvo a través de console.log (esto es salida de depuración en JS). Si usa no JS, entonces imprima X, Y, Z usted mismo usando las herramientas de su idioma. El resultado que obtuvimos en la consola: [20, 15, 9, 1], todo coincide con el resultado que calculamos anteriormente. Puede tener una pregunta, ¿por qué obtener el mismo resultado al multiplicar el vector por una matriz especial, si lo obtuvimos mucho más fácil al sumar el vector con un componente compensado? La respuesta no es la más simple y la discutiremos con más detalle, pero ahora se puede notar que, como se discutió anteriormente, podemos combinar matrices con diferentes transformaciones entre ellas,reduciendo así muchos cálculos. En el ejemplo anterior, creamos la matriz de traducciónMatriz como una matriz manualmente y sustituimos el desplazamiento necesario allí, pero como usaremos a menudo esta y otras matrices, vamos a ponerla en un método en la clase Matriz y pasarle el desplazamiento con argumentos:

static getTranslation(dx, dy, dz) {
  return [
    [1, 0, 0, dx],
    [0, 1, 0, dy],
    [0, 0, 1, dz],
    [0, 0, 0, 1],
  ]
}

Eche un vistazo más de cerca a la matriz de desplazamiento, verá que dx, dy, dz están en la última columna y si observamos el código para multiplicar la matriz por un vector, notaremos que esta columna se multiplica por el componente W del vector. Y si fuera, por ejemplo, 0, entonces dx, dy, dz, multiplicaríamos por 0 y el movimiento no funcionaría. Pero podemos hacer W igual a 0 si queremos almacenar la dirección en la clase Vector, porque es imposible mover la dirección, por lo que nos protegeríamos, e incluso si multiplicamos dicha dirección por la matriz de desplazamiento, esto no romperá el vector de dirección, porque todo el movimiento se multiplicará por 0.

Total podemos aplicar dicha regla, creamos una ubicación como esta:

new Vector(x, y, z, 1) // 1    ,

Y crearemos la dirección así:

new Vector(x, y, z, 0)

Entonces podemos distinguir entre ubicación y dirección, y cuando multiplicamos la dirección por la matriz de desplazamiento, no rompemos accidentalmente el vector de dirección.

Vértices e índices

Antes de ver qué son otras matrices, veremos un poco cómo aplicar nuestros conocimientos existentes para mostrar algo tridimensional en la pantalla. Todo lo que dedujimos antes de esto son líneas y píxeles. Pero ahora usemos estas herramientas para derivar, por ejemplo, un cubo. Para hacer esto, necesitamos descubrir en qué consiste un modelo tridimensional. El componente más básico de cualquier modelo 3D son los puntos (llamaremos a los vértices a continuación) a lo largo de los cuales podemos dibujarlo, estos son, de hecho, muchos vectores de ubicación, que, si los conectamos correctamente con líneas, obtenemos un modelo 3D (cuadrícula de modelo ) en la pantalla, será sin textura y sin muchas otras propiedades, pero todo tiene su tiempo. Eche un vistazo al cubo que queremos generar e intente comprender cuántos vértices tiene: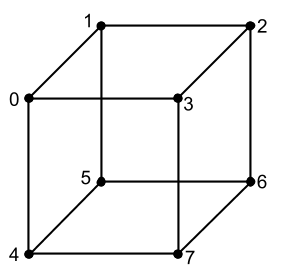

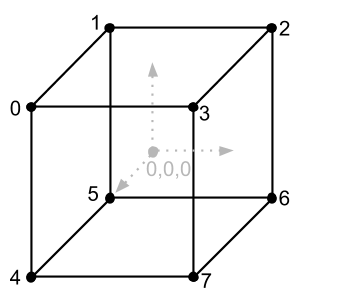
En la imagen vemos que el cubo tiene 8 vértices (por conveniencia, los numeré). Y todos los vértices están interconectados por líneas (bordes del cubo). Es decir, para describir el cubo y dibujarlo con líneas, necesitamos 8 coordenadas de cada vértice, y también necesitamos especificar desde qué vértice a qué línea dibujar, para hacer un cubo, porque si conectamos los vértices incorrectamente, por ejemplo, dibuje una línea desde el vértice 0 al vértice 6, entonces definitivamente no será un cubo, sino otro objeto. Describamos ahora las coordenadas de cada uno de los 8 vértices. En los gráficos modernos, los modelos 3D pueden constar de decenas de miles de vértices y, por supuesto, nadie los prescribe manualmente. Los modelos se dibujan en editores 3D, y cuando se exporta el modelo 3D, ya tiene todos los vértices en su código, solo necesitamos cargarlos y dibujarlos, pero por ahora estamos aprendiendo y no podemos leer los formatos de los modelos 3D, por lo que describiremos el cubo manualmente.El es muy simple.

Imagine que el cubo de arriba está en el centro de coordenadas, su centro está en el punto 0, 0, 0 y debería mostrarse alrededor de este centro:

Comencemos desde el vértice 0, y dejemos que nuestro cubo sea muy pequeño para no escribir valores grandes ahora, las dimensiones de mi cubo serán 2 de ancho, 2 de alto y 2 de profundidad, es decir. 2 por 2 por 2. La imagen muestra que el vértice 0 está ligeramente a la izquierda del centro 0, 0, 0, por lo que estableceré X = -1, porque a la izquierda, la X más pequeña, también el vértice 0 es ligeramente más alto que el centro 0, 0, 0, y en nuestro sistema de coordenadas cuanto mayor sea la ubicación, mayor Y, estableceré mi vértice Y = 1, también Z para el vértice 0, un poco más cerca de la pantalla con respecto al punto 0, 0, 0, por lo que será igual a Z = 1, porque en el sistema de coordenadas diestro, Z aumenta con el acercamiento del objeto. Como resultado, obtuvimos las coordenadas -1, 1, 1 para el vértice cero, hagamos lo mismo para los 7 vértices restantes y guárdelo en una matriz para que pueda trabajar con ellos en un bucle,Obtuve este resultado (se puede crear una matriz debajo de las clases Drawer, Vector, Marix):

// Cube vertices
const vertices = [
  new Vector(-1, 1, 1), // 0 
  new Vector(-1, 1, -1), // 1 
  new Vector(1, 1, -1), // 2 
  new Vector(1, 1, 1), // 3 
  new Vector(-1, -1, 1), // 4 
  new Vector(-1, -1, -1), // 5 
  new Vector(1, -1, -1), // 6 
  new Vector(1, -1, 1), // 7 
];

Puse cada vértice en una instancia de la clase Vector, esta no es la mejor opción para el rendimiento (mejor en una matriz), pero ahora nuestro objetivo es descubrir cómo funciona todo.

Tomemos ahora las coordenadas de los vértices del cubo como píxeles que dibujaremos en la pantalla, en este caso vemos que el tamaño del cubo es de 2 por 2 por 2 píxeles. Creamos un cubo tan pequeño para que mire el trabajo de la matriz de escala, con la cual la incrementaremos. En el futuro, es una muy buena práctica hacer modelos pequeños, incluso más pequeños que los nuestros, para aumentarlos al tamaño deseado con escalares no muy diferentes.

Es solo que dibujar los puntos del cubo con píxeles no es muy claro, porque todo lo que veremos son 8 píxeles, uno para cada vértice, es mucho mejor dibujar un cubo con líneas usando la función drawLine del artículo anterior. Pero para esto necesitamos entender de qué vértices a qué líneas pasamos. Observe nuevamente la imagen del cubo con los índices y veremos que consta de 12 líneas (o bordes). También es muy fácil ver que conocemos las coordenadas del principio y el final de cada línea. Por ejemplo, una de las líneas (superior cercana) debe dibujarse desde el vértice 0 al vértice 3, o desde las coordenadas [-1, 1, 1] a las coordenadas [1, 1, 1]. Tendremos que escribir información sobre cada línea en el código mirando manualmente la imagen del cubo, pero ¿cómo hacerlo correctamente? Si tenemos 12 líneas y cada línea tiene un principio y un final, es decir 2 puntos, entonces,para dibujar un cubo necesitamos 24 puntos? Esta es la respuesta correcta, pero echemos un vistazo a la imagen del cubo nuevamente y prestemos atención al hecho de que cada línea del cubo tiene vértices comunes, por ejemplo, en el vértice 0 3 líneas están conectadas, y así con cada vértice. Podemos ahorrar memoria y no anotar las coordenadas del principio y el final de cada línea, solo cree una matriz y especifique los índices de vértice de la matriz de vértices en la que comienzan y terminan estas líneas. Creemos una matriz de este tipo y describámosla solo con índices de vértices, 2 índices por línea (el principio de la línea y el final). Y un poco más lejos, cuando dibujamos estas líneas, podemos obtener fácilmente sus coordenadas de la matriz de vértices. Mi conjunto de líneas (lo llamé bordes, porque estos son los bordes del cubo) Creé un conjunto de vértices a continuación y se ve así:Pero echemos un vistazo a la imagen del cubo nuevamente y prestemos atención al hecho de que cada línea del cubo tiene vértices comunes, por ejemplo, en el vértice 0 3 líneas están conectadas, y así con cada vértice. Podemos ahorrar memoria y no anotar las coordenadas del principio y el final de cada línea, solo cree una matriz y especifique los índices de vértice de la matriz de vértices en la que comienzan y terminan estas líneas. Creemos una matriz de este tipo y describámosla solo con índices de vértices, 2 índices por línea (el principio de la línea y el final). Y un poco más lejos, cuando dibujamos estas líneas, podemos obtener fácilmente sus coordenadas de la matriz de vértices. Mi conjunto de líneas (lo llamé bordes, porque estos son los bordes del cubo) Creé un conjunto de vértices a continuación y se ve así:Pero echemos un vistazo a la imagen del cubo nuevamente y prestemos atención al hecho de que cada línea del cubo tiene vértices comunes, por ejemplo, en el vértice 0 3 líneas están conectadas, y así con cada vértice. Podemos ahorrar memoria y no anotar las coordenadas del principio y el final de cada línea, solo cree una matriz y especifique los índices de vértice de la matriz de vértices en la que comienzan y terminan estas líneas. Creemos una matriz de este tipo y describámosla solo con índices de vértices, 2 índices por línea (el principio de la línea y el final). Y un poco más lejos, cuando dibujamos estas líneas, podemos obtener fácilmente sus coordenadas de la matriz de vértices. Mi conjunto de líneas (lo llamé bordes, porque estos son los bordes del cubo) Creé un conjunto de vértices a continuación y se ve así:y así con cada vértice. Podemos ahorrar memoria y no anotar las coordenadas del principio y el final de cada línea, solo cree una matriz y especifique los índices de vértice de la matriz de vértices en la que comienzan y terminan estas líneas. Creemos una matriz de este tipo y describámosla solo con índices de vértices, 2 índices por línea (el principio de la línea y el final). Y un poco más lejos, cuando dibujamos estas líneas, podemos obtener fácilmente sus coordenadas de la matriz de vértices. Mi conjunto de líneas (lo llamé bordes, porque estos son los bordes del cubo) Creé un conjunto de vértices a continuación y se ve así:y así con cada vértice. Podemos ahorrar memoria y no anotar las coordenadas del principio y el final de cada línea, solo cree una matriz y especifique los índices de vértice de la matriz de vértices en la que comienzan y terminan estas líneas. Creemos una matriz de este tipo y describámosla solo con índices de vértices, 2 índices por línea (el principio de la línea y el final). Y un poco más lejos, cuando dibujamos estas líneas, podemos obtener fácilmente sus coordenadas de la matriz de vértices. Mi conjunto de líneas (lo llamé bordes, porque estos son los bordes del cubo) Creé un conjunto de vértices a continuación y se ve así:2 índices en cada línea (el principio de la línea y el final). Y un poco más lejos, cuando dibujamos estas líneas, podemos obtener fácilmente sus coordenadas de la matriz de vértices. Mi conjunto de líneas (lo llamé bordes, porque estos son los bordes del cubo) Creé un conjunto de vértices a continuación y se ve así:2 índices en cada línea (el principio de la línea y el final). Y un poco más lejos, cuando dibujamos estas líneas, podemos obtener fácilmente sus coordenadas de la matriz de vértices. Mi conjunto de líneas (lo llamé bordes, porque estos son los bordes del cubo) Creé un conjunto de vértices a continuación y se ve así:

// Cube edges
const edges = [
  [0, 1],
  [1, 2],
  [2, 3],
  [3, 0],

  [0, 4],
  [1, 5],
  [2, 6],
  [3, 7],

  [4, 5],
  [5, 6],
  [6, 7],
  [7, 4],
];

Hay 12 pares de índices en esta matriz, 2 índices de vértice por línea.

Conozcamos otra matriz que aumentará nuestro cubo y, finalmente, intente dibujarlo en la pantalla. La Matriz de escala se ve así:

[\begin{matrix} s x & 0 & 0 & 0 \\ 0 & s y & 0 & 0 \\ 0 & 0 & s z & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$\begin{bmatrix}sx&0&0&0\\0&sy&0&0\\0&0&sz&0\\0&0&0&1\end{bmatrix}$

Los parámetros sx, sy, sz en la diagonal principal significan cuántas veces queremos aumentar el objeto. Si sustituimos 10, 10, 10 en la matriz en lugar de sx, sy, sz y multiplicamos esta matriz por los vértices del cubo, esto hará que nuestro cubo sea diez veces más grande y ya no será 2 por 2 por 2, sino 20 por 20 por 20.

Para la matriz de escala, así como para la matriz de desplazamiento, implementamos el método en la clase Matrix, que devolverá la matriz con los argumentos ya sustituidos:

static getScale(sx, sy, sz) {
  return [
    [sx, 0, 0, 0],
    [0, sy, 0, 0],
    [0, 0, sz, 0],
    [0, 0, 0, 1],
  ]
}

Transportador de visualización

Si ahora tratamos de dibujar un cubo con líneas usando las coordenadas actuales de los vértices, obtendremos un cubo muy pequeño de dos píxeles en la esquina superior izquierda de la pantalla, porque El origen del lienzo está ahí. Pasemos por todos los vértices del cubo y multiplíquelos por la matriz de escala para agrandar el cubo, y luego por la matriz de desplazamiento para ver el cubo no en la esquina superior izquierda, sino en el medio de la pantalla, tengo el código para enumerar los vértices con la multiplicación de la matriz a continuación. matriz de bordes, y se ve así:

const sceneVertices = []
for(let i = 0 ; i < vertices.length ; i++) {
  let vertex = Matrix.multiplyVector(
    Matrix.getScale(100, 100, 100),
    vertices[i]
  );

  vertex = Matrix.multiplyVector(
    Matrix.getTranslation(400, -300, 0),
    vertex
  );

  sceneVertices.push(vertex);
}

Tenga en cuenta que no cambiamos los vértices originales del cubo, sino que guardamos el resultado de la multiplicación en el conjunto de escena SceneVertices, porque es posible que queramos dibujar varios cubos de diferentes tamaños en diferentes coordenadas, y si cambiamos las coordenadas iniciales, entonces no podremos dibujar el siguiente cubo, t .a. no hay nada desde donde comenzar, las coordenadas iniciales serán corrompidas por el primer cubo. En el código anterior, aumenté el cubo original en 100 veces en todas las direcciones, gracias a la multiplicación de todos los vértices por la matriz de escala con argumentos 100, 100, 100, y también moví todos los vértices del cubo hacia la derecha y hacia abajo por 400 y -300 píxeles, respectivamente, ya que tenemos los tamaños de lienzo del artículo anterior son 800 por 600, será solo la mitad del ancho y la altura del área de dibujo, en otras palabras, el centro.

Hemos terminado con los vértices hasta ahora, pero aún necesitamos dibujar todo esto usando drawLine y la matriz de bordes, escriba otro bucle debajo del bucle de vértices para iterar sobre los bordes y dibujar todas las líneas en él:

drawer.clearSurface()

for (let i = 0, l = edges.length ; i < l ; i++) {
  const e = edges[i]

  drawer.drawLine(
    sceneVertices[e[0]].x,
    sceneVertices[e[0]].y,
    sceneVertices[e[1]].x,
    sceneVertices[e[1]].y,
    0, 0, 255
  )
}

ctx.putImageData(imageData, 0, 0)

Recuerde que en el último artículo comenzamos todo el dibujo despejando la pantalla del estado anterior llamando al método clearSurface, luego itero sobre todas las caras del cubo y dibujo el cubo con líneas azules (0, 0, 255), y tomo las coordenadas de las líneas de la matriz sceneVertices, t .a. ya hay vértices escalados y movidos en el ciclo anterior, pero los índices de estos vértices coinciden con los índices de los vértices originales de la matriz de vértices, porque Los procesé y los puse en la matriz de SceneVertices sin cambiar el orden.

Si ejecutamos el código ahora, no veremos nada en la pantalla. Esto se debe a que en nuestro sistema de coordenadas, Y mira hacia arriba y en el sistema de coordenadas, el lienzo mira hacia abajo. Resulta que existe nuestro cubo, pero está fuera de la pantalla y para solucionarlo, debemos voltear la imagen en Y (espejo) antes de dibujar un píxel en la clase Drawer. Hasta ahora, esta opción será suficiente para nosotros, como resultado, el código para dibujar un píxel para mí se ve así:

drawPixel(x, y, r, g, b) {
  const offset = (this.width * -y + x) * 4;

  if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
    this.surface[offset] = r;
    this.surface[offset + 1] = g;
    this.surface[offset + 2] = b;
    this.surface[offset + 3] = 255;
  }
}

Se puede ver que en la fórmula para obtener el desplazamiento, Y ahora tiene un signo menos y el eje ahora se ve en la dirección que necesitamos, también en este método agregué una verificación para ir más allá de los límites de la matriz de píxeles. Algunas otras optimizaciones aparecieron en la clase Drawer debido a los comentarios en el artículo anterior, por lo que publico toda la clase Drawer con algunas optimizaciones y puede reemplazar el antiguo Drawer por este:

Código de clase de cajón mejorado

class Drawer {
  surface = null;
  width = 0;
  height = 0;

  constructor(surface, width, height) {
    this.surface = surface;
    this.width = width;
    this.height = height;
  }

  drawPixel(x, y, r, g, b) {
    const offset = (this.width * -y + x) * 4;

    if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
      this.surface[offset] = r;
      this.surface[offset + 1] = g;
      this.surface[offset + 2] = b;
      this.surface[offset + 3] = 255;
    }
  }

  drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
    const round = Math.trunc;
    x1 = round(x1);
    y1 = round(y1);
    x2 = round(x2);
    y2 = round(y2);

    const c1 = y2 - y1;
    const c2 = x2 - x1;

    const length = Math.max(
      Math.abs(c1),
      Math.abs(c2)
    );

    const xStep = c2 / length;
    const yStep = c1 / length;

    for (let i = 0 ; i <= length ; i++) {
      this.drawPixel(
        Math.trunc(x1 + xStep * i),
        Math.trunc(y1 + yStep * i),
        r, g, b,
      );
    }
  }

  clearSurface() {
    const surfaceSize = this.width * this.height * 4;
    for (let i = 0; i < surfaceSize; i++) {
      this.surface[i] = 0;
    }
  }
}

const drawer = new Drawer(
  imageData.data,
  imageData.width,
  imageData.height
);

Si ejecuta el código ahora, aparecerá la siguiente imagen en la pantalla:

Aquí puedes ver que hay un cuadrado en el centro, aunque esperábamos obtener un cubo, ¿qué pasa? De hecho, este es el cubo, simplemente se coloca perfectamente perfectamente alineado con una de las caras (laterales) hacia nosotros, por lo que no vemos el resto. Además, todavía no nos hemos familiarizado con las proyecciones y, por lo tanto, la cara posterior del cubo no se vuelve más pequeña con la distancia, como en la vida real. Para asegurarnos de que este sea realmente un cubo, gírelo un poco para que se vea como la imagen que vimos anteriormente cuando formamos la matriz de vértices. Para rotar la imagen 3D, puede usar 3 matrices especiales, porque podemos rotar alrededor de uno de los ejes X, Y o Z, lo que significa que para cada eje habrá su propia matriz de rotación (hay otras formas de rotación, pero este es el tema de los próximos artículos). Así es como se ven estas matrices:

R_{x} (a) = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & c o s (a) & - s i n (a) & 0 \\ 0 & s i n (a) & c o s (a) & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$R_x(a)=\begin{bmatrix}1&0&0&0\\0&cos(a)&-sin(a)&0\\0&sin(a)&cos(a)&0\\0&0&0&1\end{bmatrix}$

Matriz de rotación del eje X

R_{y} (a) [\begin{matrix} c o s (a) & 0 & s i n (a) & 0 \\ 0 & 1 & 0 & 0 \\ - s i n (a) & 0 & c o s (a) & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$R_y(a)\begin{bmatrix}cos(a)&0&sin(a)&0\\0&1&0&0\\-sin(a)&0&cos(a)&0\\0&0&0&1\end{bmatrix}$

Matriz de rotación del eje Y

R_{z} (a) [\begin{matrix} c o s (a) & - s i n (a) & 0 & 0 \\ s i n (a) & c o s (a) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$R_z(a)\begin{bmatrix}cos(a)&-sin(a)&0&0\\sin(a)&cos(a)&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}$

Matriz de rotación del eje Z

Si multiplicamos los vértices del cubo por una de estas matrices, el cubo rotará en el ángulo especificado (a) alrededor del eje, la matriz de rotación alrededor de la cual elegiremos. Hay algunas características al girar varios ejes a la vez, y los veremos a continuación. Como puede ver en el ejemplo de la matriz, usan 2 funciones sin y cos, y JavaScript ya tiene una función para calcular Math.sin (a) y Math.cos (a), pero funcionan con medidas de ángulos en radianes, lo que puede no parecer lo más conveniente si queremos rotar el modelo. Por ejemplo, es mucho más conveniente para mí girar 90 grados (medida de grado), lo que en una medida en radianes significaráPi / 2(También hay un valor aproximado de Pi en JS, esta es la constante Math.PI). Agreguemos 3 métodos a la clase Matrix para obtener matrices de rotación, con un ángulo de rotación aceptado en grados, que convertiremos a radianes, porque son necesarios para que las funciones sin / cos funcionen:

static getRotationX(angle) {
  const rad = Math.PI / 180 * angle;

  return [
    [1, 0, 0, 0],
    [0, Math.cos(rad), -Math.sin(rad), 0],
    [0, Math.sin(rad), Math.cos(rad), 0],
    [0, 0, 0, 1],
  ];
}

static getRotationY(angle) {
  const rad = Math.PI / 180 * angle;

  return [
    [Math.cos(rad), 0, Math.sin(rad), 0],
    [0, 1, 0, 0],
    [-Math.sin(rad), 0, Math.cos(rad), 0],
    [0, 0, 0, 1],
  ];
}

static getRotationZ(angle) {
  const rad = Math.PI / 180 * angle;

  return [
    [Math.cos(rad), -Math.sin(rad), 0, 0],
    [Math.sin(rad), Math.cos(rad), 0, 0],
    [0, 0, 1, 0],
    [0, 0, 0, 1],
  ];
}

Los 3 métodos comienzan con la conversión de grados a radianes, después de lo cual sustituimos el ángulo de rotación en radianes en la matriz de rotación, pasando los ángulos a las funciones sen y cos. Por qué la matriz es así, puede leer más sobre el centro en los artículos temáticos, con una explicación muy detallada, de lo contrario puede percibir estas matrices como fórmulas que se han calculado para nosotros y podemos estar seguros de que están funcionando.

Arriba en el código, implementamos 2 ciclos, el primero convierte vértices, el segundo dibuja líneas por índices de vértices, como resultado, obtenemos una imagen de los vértices en la pantalla, y llamemos a esta sección del código la tubería de visualización. El transportador porque tomamos el pico y a su vez hacemos diferentes operaciones con él, escala, cambio, rotación, renderizado, como en un transportador industrial normal. Ahora agreguemos al primer ciclo en la tubería de visualización, además de la escala, la rotación alrededor de los ejes. Primero, giraré alrededor de X, luego alrededor de Y, luego aumentaré el modelo y lo moveré (las últimas 2 acciones ya están allí), por lo que todo el código del bucle será así:

for(let i = 0 ; i < vertices.length ; i++) {
  let vertex = Matrix.multiplyVector(
    Matrix.getRotationX(20),
    vertices[i]
  );

  vertex = Matrix.multiplyVector(
    Matrix.getRotationY(20),
    vertex
  );

  vertex = Matrix.multiplyVector(
    Matrix.getScale(100, 100, 100),
    vertex
  );

  vertex = Matrix.multiplyVector(
    Matrix.getTranslation(400, -300, 0),
    vertex
  );

  sceneVertices.push(vertex);
}

En este ejemplo, roté todos los vértices alrededor del eje X en 20 grados, luego alrededor de Y en 20 grados y ya tenía 2 transformaciones restantes. Si hiciste todo correctamente, tu cubo ahora debería verse tridimensional:

Girar los ejes tiene una característica, por ejemplo, si gira el cubo primero alrededor del eje Y y luego alrededor del eje X, los resultados serán diferentes:


Gire 20 grados alrededor de X, luego 20 grados alrededor de Y	Gire 20 grados alrededor de Y, luego 20 grados alrededor de X

Hay otras características, por ejemplo, si gira el cubo 90 grados en el eje X, luego 90 grados en el eje Y y finalmente 90 grados alrededor del eje Z, entonces la última rotación alrededor de Z cancelará la rotación alrededor de X, y obtendrá el mismo el resultado es como si acabara de girar la figura 90 grados alrededor del eje Y. Para ver por qué sucede esto, tome cualquier objeto rectangular (o cúbico) en sus manos (por ejemplo, el cubo de Rubik ensamblado), recuerde la posición inicial del objeto y gírelo 90 grados primero alrededor de X imaginaria, y luego 90 grados alrededor de Y y 90 grados alrededor de Z y recuerde en qué lado se ha convertido para usted, luego comience desde la posición inicial que recordaba anteriormente y haga lo mismo, quitando las vueltas de X y Z, gire solo alrededor Y: verá que el resultado es el mismo.Ahora no resolveremos este problema y entraremos en detalles, esta rotación es actualmente completamente satisfactoria para nosotros, pero mencionaremos este problema en la tercera parte (si desea comprender más ahora, intente buscar artículos en el centro mediante la consulta "bloqueo con bisagra") .

Ahora optimicemos un poco nuestro código, se mencionó anteriormente que las transformaciones matriciales se pueden combinar entre sí multiplicando las matrices de transformación. Intentemos no multiplicar cada vector primero por la matriz de rotación alrededor de X, luego alrededor de Y, luego escalar y al final del movimiento, y primero, antes del ciclo, multiplicamos todas las matrices, y en el ciclo multiplicaremos cada vértice por solo una matriz resultante, tengo el código salió así:

let matrix = Matrix.getRotationX(20);

matrix = Matrix.multiply(
  Matrix.getRotationY(20),
  matrix
);

matrix = Matrix.multiply(
  Matrix.getScale(100, 100, 100),
  matrix,
);

matrix = Matrix.multiply(
  Matrix.getTranslation(400, -300, 0),
  matrix,
);

const sceneVertices = [];
for(let i = 0 ; i < vertices.length ; i++) {
  let vertex = Matrix.multiplyVector(
    matrix,
    vertices[i]
  );

  sceneVertices.push(vertex);
}

En este ejemplo, la combinación de transformaciones se realiza 1 vez antes del ciclo y, por lo tanto, solo tenemos 1 multiplicación de matriz con cada vértice. Si ejecuta este código, el patrón del cubo debe permanecer igual.

Agreguemos la animación más simple, es decir, cambiaremos el ángulo de rotación alrededor del eje Y en el intervalo, por ejemplo, cambiaremos el ángulo de rotación alrededor del eje Y en 1 grado, cada 100 milisegundos. Para hacer esto, coloque el código de la canalización de visualización en la función setInterval, que usamos por primera vez en el primer artículo. El código de canalización de animación se ve así:

let angle = 0
setInterval(() => {
  let matrix = Matrix.getRotationX(20)

  matrix = Matrix.multiply(
    Matrix.getRotationY(angle += 1),
    matrix
  )

  matrix = Matrix.multiply(
    Matrix.getScale(100, 100, 100),
    matrix,
  )

  matrix = Matrix.multiply(
    Matrix.getTranslation(400, -300, 0),
    matrix,
  )

  const sceneVertices = []
  for(let i = 0 ; i < vertices.length ; i++) {
    let vertex = Matrix.multiplyVector(
      matrix,
      vertices[i]
    )

    sceneVertices.push(vertex)
  }

  drawer.clearSurface()

  for (let i = 0, l = edges.length ; i < l ; i++) {
    const e = edges[i]

    drawer.drawLine(
      sceneVertices[e[0]].x,
      sceneVertices[e[0]].y,
      sceneVertices[e[1]].x,
      sceneVertices[e[1]].y,
      0, 0, 255
    )
  }

  ctx.putImageData(imageData, 0, 0)
}, 100)

El resultado debería ser así:

Lo último que haremos en esta parte es mostrar los ejes del sistema de coordenadas en la pantalla para que sea visible alrededor del cual gira nuestro cubo. Dibujamos el eje Y desde el centro hacia arriba, 200 píxeles de largo, el eje X, a la derecha, también 200 píxeles de largo, y el eje Z, dibujamos 150 píxeles hacia abajo y hacia la izquierda (en diagonal), como se muestra al comienzo del artículo en la figura del sistema de coordenadas derecho . Comencemos con la parte más simple, estos son los ejes X, Y, porque su línea cambia en una sola dirección. Después del bucle que dibuja el cubo (bucle de bordes) agregue la representación del eje X, Y:

const center = new Vector(400, -300, 0)
drawer.drawLine(
  center.x, center.y,
  center.x, center.y + 200,
  150, 150, 150
)

drawer.drawLine(
  center.x, center.y,
  center.x + 200, center.y,
  150, 150, 150
)

El vector central es el centro de la ventana de dibujo, porque tenemos las dimensiones actuales de 800 por 600 y -300 para Y, indiqué, porque la función drawPixel voltea Y y hace que su dirección sea adecuada para el lienzo (en lienzo, Y mira hacia abajo). Luego dibujamos 2 ejes usando drawLine, primero desplazando Y 200 píxeles hacia arriba (final de la línea del eje Y), luego X 200 píxeles hacia la derecha (final de la línea del eje X). Resultado: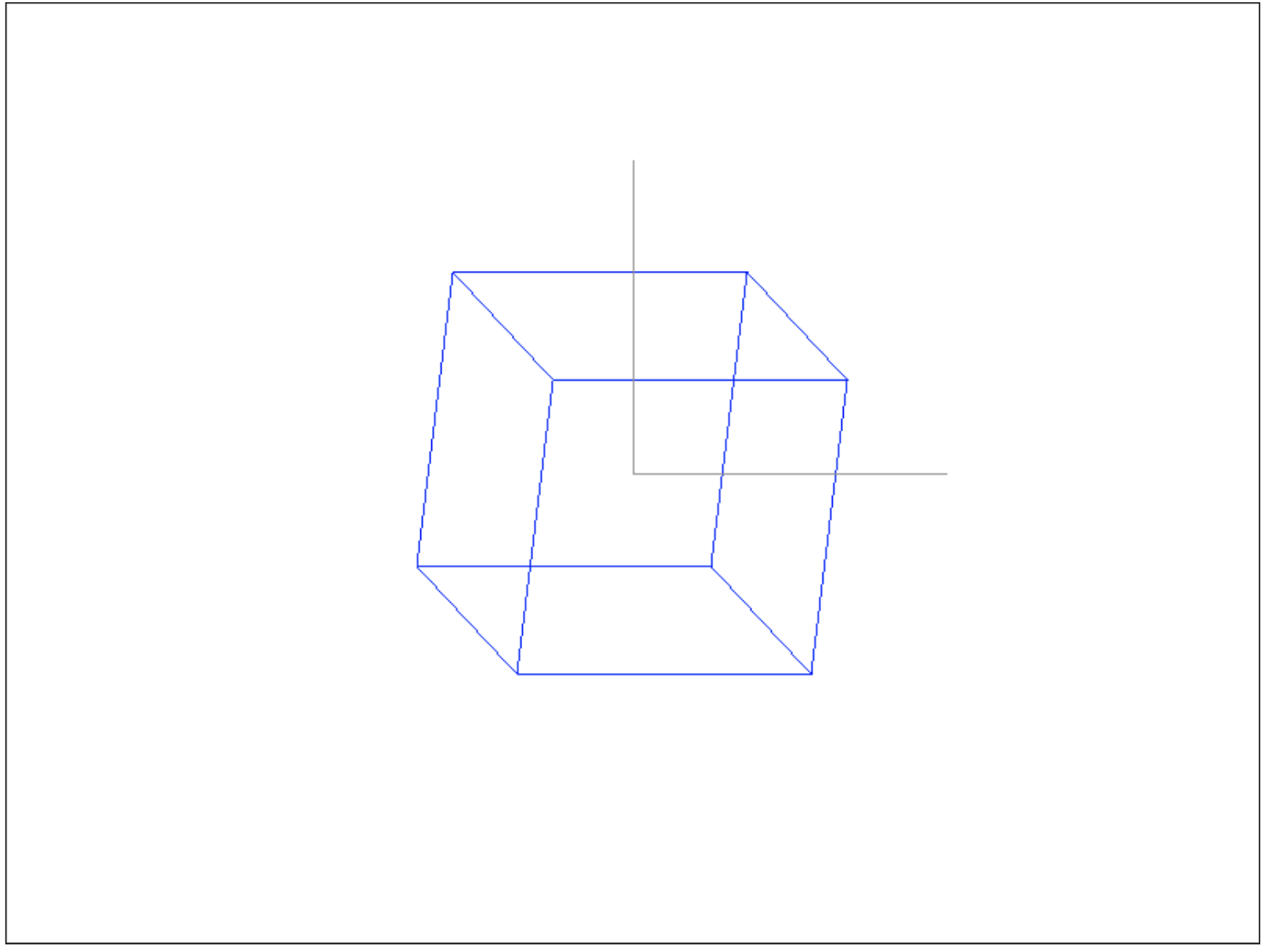

Ahora dibujemos la línea del eje Z, es diagonal hacia abajo \ izquierda y su vector de desplazamiento será [-1, -1, 0] y también necesitamos dibujar una línea con una longitud de 150 píxeles, es decir el vector de desplazamiento [-1, -1, 0] debe tener una longitud de 150, la primera opción es [-150, -150, 0], pero si calculamos la longitud de dicho vector, será aproximadamente 212 píxeles. Anteriormente en este artículo, discutimos cómo obtener correctamente un vector de la longitud deseada. En primer lugar, debemos normalizarlo para obtener una longitud de 1, y luego multiplicar por el escalar la longitud que queremos obtener, en nuestro caso es 150. Y, por último, resumimos las coordenadas del centro de la pantalla y el vector de desplazamiento del eje Z, de modo que llegamos a donde La línea del eje Z debería terminar. Escribamos el código, después del código de salida de los 2 ejes anteriores para dibujar la línea del eje Z:

const zVector = new Vector(-1, -1, 0);
const zCoords = Vector.add(
  center,
  zVector.normalize().multiplyByScalar(150)
);
drawer.drawLine(
  center.x, center.y,
  zCoords.x, zCoords.y,
  150, 150, 150
);

Y como resultado, obtienes los 3 ejes de la longitud deseada:

En este ejemplo, el eje Z solo muestra qué sistema de coordenadas tenemos, lo dibujamos diagonalmente para que se pueda ver, porque El eje Z real es perpendicular a nuestra mirada, y podríamos dibujarlo con un punto en la pantalla, lo que no sería hermoso.

En total, en este artículo, básicamente descubrimos sistemas de coordenadas, vectores y con algunas operaciones sobre ellos, matrices y sus roles en las transformaciones de coordenadas, clasificamos los vértices y escribimos una tubería simple para visualizar el cubo y los ejes del sistema de coordenadas, fijando la teoría con la práctica. Todo el código de la aplicación está disponible bajo el spoiler:

Código para toda la aplicación

const ctx = document.getElementById('surface').getContext('2d');
const imageData = ctx.createImageData(800, 600);

class Vector {
  x = 0;
  y = 0;
  z = 0;
  w = 1;

  constructor(x, y, z, w = 1) {
    this.x = x;
    this.y = y;
    this.z = z;
    this.w = w;
  }

  multiplyByScalar(s) {
    this.x *= s;
    this.y *= s;
    this.z *= s;

    return this;
  }

  static add(v1, v2) {
    return new Vector(
      v1.x + v2.x,
      v1.y + v2.y,
      v1.z + v2.z,
    );
  }

  getLength() {
    return Math.sqrt(
      this.x * this.x + this.y * this.y + this.z * this.z
    );
  }

  normalize() {
    const length = this.getLength();

    this.x /= length;
    this.y /= length;
    this.z /= length;

    return this;
  }
}

class Matrix {
  static multiply(a, b) {
    const m = [
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
    ];

    for (let i = 0 ; i < 4 ; i++) {
      for(let j = 0 ; j < 4 ; j++) {
        m[i][j] = a[i][0] * b[0][j] +
          a[i][1] * b[1][j] +
          a[i][2] * b[2][j] +
          a[i][3] * b[3][j];
      }
    }

    return m;
  }

  static getRotationX(angle) {
    const rad = Math.PI / 180 * angle;

    return [
      [1, 0, 0, 0],
      [0, Math.cos(rad), -Math.sin(rad), 0],
      [0, Math.sin(rad), Math.cos(rad), 0],
      [0, 0, 0, 1],
    ];
  }

  static getRotationY(angle) {
    const rad = Math.PI / 180 * angle;

    return [
      [Math.cos(rad), 0, Math.sin(rad), 0],
      [0, 1, 0, 0],
      [-Math.sin(rad), 0, Math.cos(rad), 0],
      [0, 0, 0, 1],
    ];
  }

  static getRotationZ(angle) {
    const rad = Math.PI / 180 * angle;

    return [
      [Math.cos(rad), -Math.sin(rad), 0, 0],
      [Math.sin(rad), Math.cos(rad), 0, 0],
      [0, 0, 1, 0],
      [0, 0, 0, 1],
    ];
  }

  static getTranslation(dx, dy, dz) {
    return [
      [1, 0, 0, dx],
      [0, 1, 0, dy],
      [0, 0, 1, dz],
      [0, 0, 0, 1],
    ];
  }

  static getScale(sx, sy, sz) {
    return [
      [sx, 0, 0, 0],
      [0, sy, 0, 0],
      [0, 0, sz, 0],
      [0, 0, 0, 1],
    ];
  }

  static multiplyVector(m, v) {
    return new Vector(
      m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
      m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
      m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
      m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
    );
  }
}

class Drawer {
  surface = null;
  width = 0;
  height = 0;

  constructor(surface, width, height) {
    this.surface = surface;
    this.width = width;
    this.height = height;
  }

  drawPixel(x, y, r, g, b) {
    const offset = (this.width * -y + x) * 4;

    if (x >= 0 && x < this.width && -y >= 0 && -y < this.height) {
      this.surface[offset] = r;
      this.surface[offset + 1] = g;
      this.surface[offset + 2] = b;
      this.surface[offset + 3] = 255;
    }
  }
  drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
    const round = Math.trunc;
    x1 = round(x1);
    y1 = round(y1);
    x2 = round(x2);
    y2 = round(y2);

    const c1 = y2 - y1;
    const c2 = x2 - x1;

    const length = Math.max(
      Math.abs(c1),
      Math.abs(c2)
    );

    const xStep = c2 / length;
    const yStep = c1 / length;

    for (let i = 0 ; i <= length ; i++) {
      this.drawPixel(
        Math.trunc(x1 + xStep * i),
        Math.trunc(y1 + yStep * i),
        r, g, b,
      );
    }
  }

  clearSurface() {
    const surfaceSize = this.width * this.height * 4;
    for (let i = 0; i < surfaceSize; i++) {
      this.surface[i] = 0;
    }
  }
}

const drawer = new Drawer(
  imageData.data,
  imageData.width,
  imageData.height
);

// Cube vertices
const vertices = [
  new Vector(-1, 1, 1), // 0 
  new Vector(-1, 1, -1), // 1 
  new Vector(1, 1, -1), // 2 
  new Vector(1, 1, 1), // 3 
  new Vector(-1, -1, 1), // 4 
  new Vector(-1, -1, -1), // 5 
  new Vector(1, -1, -1), // 6 
  new Vector(1, -1, 1), // 7 
];

// Cube edges
const edges = [
  [0, 1],
  [1, 2],
  [2, 3],
  [3, 0],

  [0, 4],
  [1, 5],
  [2, 6],
  [3, 7],

  [4, 5],
  [5, 6],
  [6, 7],
  [7, 4],
];

let angle = 0;
setInterval(() => {
  let matrix = Matrix.getRotationX(20);

  matrix = Matrix.multiply(
    Matrix.getRotationY(angle += 1),
    matrix
  );

  matrix = Matrix.multiply(
    Matrix.getScale(100, 100, 100),
    matrix,
  );

  matrix = Matrix.multiply(
    Matrix.getTranslation(400, -300, 0),
    matrix,
  );

  const sceneVertices = [];
  for(let i = 0 ; i < vertices.length ; i++) {
    let vertex = Matrix.multiplyVector(
      matrix,
      vertices[i]
    );

    sceneVertices.push(vertex);
  }

  drawer.clearSurface();

  for (let i = 0, l = edges.length ; i < l ; i++) {
    const e = edges[i];

    drawer.drawLine(
      sceneVertices[e[0]].x,
      sceneVertices[e[0]].y,
      sceneVertices[e[1]].x,
      sceneVertices[e[1]].y,
      0, 0, 255
    );
  }

  const center = new Vector(400, -300, 0)
  drawer.drawLine(
    center.x, center.y,
    center.x, center.y + 200,
    150, 150, 150
  );

  drawer.drawLine(
    center.x, center.y,
    center.x + 200, center.y,
    150, 150, 150
  );

  const zVector = new Vector(-1, -1, 0, 0);
  const zCoords = Vector.add(
    center,
    zVector.normalize().multiplyByScalar(150)
  );
  drawer.drawLine(
    center.x, center.y,
    zCoords.x, zCoords.y,
    150, 150, 150
  );

  ctx.putImageData(imageData, 0, 0);
}, 100);

¿Que sigue?

En la siguiente parte, consideraremos cómo controlar la cámara y cómo hacer una proyección (cuanto más lejos esté el objeto, más pequeño es), conocer los triángulos y descubrir cómo se pueden construir modelos 3D a partir de ellos, analizar qué son las normales y por qué son necesarias.