En previsión del comienzo del curso, "Algorithms for Developers" ha preparado para usted una traducción de otro material útil.
La codificación de Huffman es un algoritmo de compresión de datos que formula la idea básica de la compresión de archivos. En este artículo, hablaremos sobre la codificación de longitud fija y variable, códigos decodificados de forma única, reglas de prefijos y la construcción de un árbol Huffman.Sabemos que cada carácter se almacena como una secuencia de 0 y 1 y toma 8 bits. Esto se denomina codificación de longitud fija porque cada carácter usa el mismo número fijo de bits para almacenar.Digamos que el texto está dado. ¿Cómo podemos reducir la cantidad de espacio requerido para almacenar un personaje?La idea básica es la codificación de longitud variable. Podemos utilizar el hecho de que algunos caracteres en el texto son más comunes que otros ( ver aquí ) para desarrollar un algoritmo que represente la misma secuencia de caracteres con menos bits. Al codificar una longitud variable, asignamos un número variable de bits a los caracteres dependiendo de la frecuencia de su aparición en este texto. En última instancia, algunos caracteres pueden ocupar solo 1 bit y otros 2 bits, 3 o más. El problema con la codificación de longitud variable es solo la posterior decodificación de la secuencia.¿Cómo, conociendo la secuencia de bits, decodificarlo de manera única?Considere la cadena "aabacdab" . Tiene 8 caracteres, y cuando se codifica una longitud fija, se necesitarán 64 bits para almacenarlo. Tenga en cuenta que la frecuencia de los caracteres "a", "b", "c" y "d" es 4, 2, 1, 1, respectivamente. Tratemos de imaginar "aabacdab" con menos bits, utilizando el hecho de que "a" es más común que "b" y "b" es más común que "c" y "d" . Para empezar, codificamos "a" usando un bit igual a 0, "b" asignamos un código de dos bits 11, y usando tres bits 100 y 011 codificamos "c" y"D" .Como resultado, tendremos éxito:Por lo tanto, codificamos la cadena "aabacdab" como 00110100011011 (0 | 0 | 11 | 0 | 100 | 011 | 0 | 11) utilizando los códigos presentados anteriormente. Sin embargo, el principal problema será la decodificación. Cuando intentamos decodificar la línea 00110100011011 , obtenemos un resultado ambiguo, ya que puede representarse como:0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
...etc.Para evitar esta ambigüedad, debemos asegurarnos de que nuestra codificación satisfaga un concepto como una regla de prefijo , lo que a su vez implica que los códigos se pueden decodificar de una sola manera. Una regla de prefijo asegura que ningún código sea el prefijo de otro. Por código, nos referimos a los bits utilizados para representar un personaje en particular. En el ejemplo anterior, 0 es el prefijo 011 , que viola la regla del prefijo. Entonces, si nuestros códigos satisfacen la regla del prefijo, entonces podemos decodificar de forma exclusiva (y viceversa).Repasemos el ejemplo anterior. Esta vez asignaremos los caracteres "a", "b", "c" y "d" Códigos que satisfacen la regla del prefijo.Con esta codificación, la cadena "aabacdab" se codificará como 00100100011010 (0 | 0 | 10 | 0 | 100 | 011 | 0 | 10) . Y aquí 00100100011010 podemos decodificar de forma única y volver a nuestra línea original "aabacdab" .Codificación Huffman
Ahora que hemos descubierto la codificación de longitud variable y una regla de prefijo, hablemos de la codificación de Huffman.El método se basa en la creación de árboles binarios. En él, un nodo puede ser finito o interno. Inicialmente, todos los nodos se consideran hojas (hojas), que representan el símbolo en sí y su peso (es decir, la frecuencia de ocurrencia). Los nodos internos contienen el peso del personaje y se refieren a dos nodos descendientes. Por acuerdo general, el bit "0" representa un seguimiento en la rama izquierda, y "1" representa a la derecha. En un árbol completo hay N hojas y N-1 nodos internos. Se recomienda que al construir un árbol Huffman, los caracteres no utilizados se descarten para obtener códigos de longitud óptima.Utilizaremos la cola de prioridad para construir el árbol Huffman, donde el nodo con la frecuencia más baja tendrá la máxima prioridad. Los pasos de construcción se describen a continuación:- Cree un nodo hoja para cada personaje y agréguelos a la cola de prioridad.
- Mientras está en línea para más de una hoja, haga lo siguiente:
- Elimine los dos nodos con la prioridad más alta (con la frecuencia más baja) de la cola;
- Cree un nuevo nodo interno donde estos dos nodos sean herederos, y la frecuencia de ocurrencia será igual a la suma de las frecuencias de estos dos nodos.
- Agregue un nuevo nodo a la cola de prioridad.
- El único nodo restante será la raíz, esto finalizará la construcción del árbol.
Imagine que tenemos un texto que consta solo de los caracteres "a", "b", "c", "d" y "e", y las frecuencias de su aparición son 15, 7, 6, 6 y 5, respectivamente. A continuación se muestran ilustraciones que reflejan los pasos del algoritmo.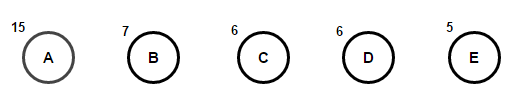
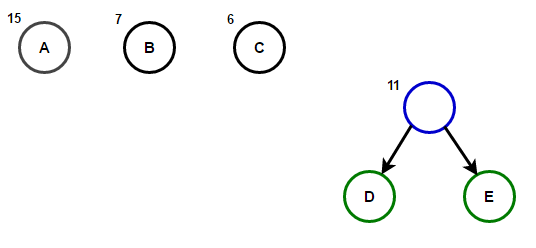
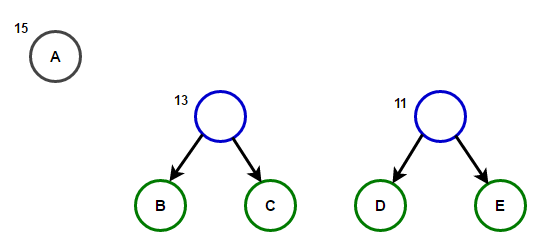
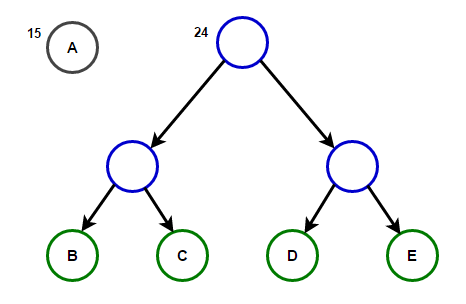
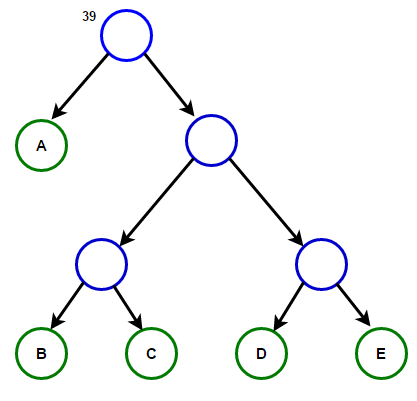 La ruta desde la raíz a cualquier nodo final almacenará el código de prefijo óptimo (también conocido como el código Huffman) correspondiente al carácter asociado con ese nodo final.
La ruta desde la raíz a cualquier nodo final almacenará el código de prefijo óptimo (también conocido como el código Huffman) correspondiente al carácter asociado con ese nodo final.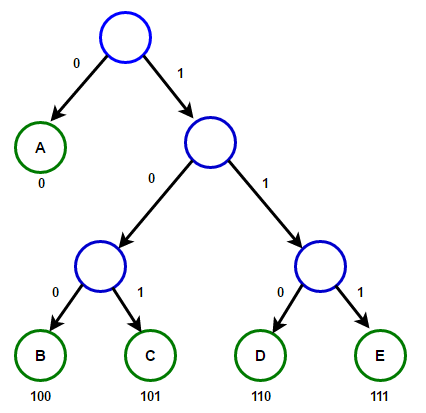 Árbol de HuffmanA continuación encontrará la implementación del algoritmo de compresión de Huffman en C ++ y Java:
Árbol de HuffmanA continuación encontrará la implementación del algoritmo de compresión de Huffman en C ++ y Java:#include <iostream>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
struct Node
{
char ch;
int freq;
Node *left, *right;
};
Node* getNode(char ch, int freq, Node* left, Node* right)
{
Node* node = new Node();
node->ch = ch;
node->freq = freq;
node->left = left;
node->right = right;
return node;
}
struct comp
{
bool operator()(Node* l, Node* r)
{
return l->freq > r->freq;
}
};
void encode(Node* root, string str,
unordered_map<char, string> &huffmanCode)
{
if (root == nullptr)
return;
if (!root->left && !root->right) {
huffmanCode[root->ch] = str;
}
encode(root->left, str + "0", huffmanCode);
encode(root->right, str + "1", huffmanCode);
}
void decode(Node* root, int &index, string str)
{
if (root == nullptr) {
return;
}
if (!root->left && !root->right)
{
cout << root->ch;
return;
}
index++;
if (str[index] =='0')
decode(root->left, index, str);
else
decode(root->right, index, str);
}
void buildHuffmanTree(string text)
{
unordered_map<char, int> freq;
for (char ch: text) {
freq[ch]++;
}
priority_queue<Node*, vector<Node*>, comp> pq;
for (auto pair: freq) {
pq.push(getNode(pair.first, pair.second, nullptr, nullptr));
}
while (pq.size() != 1)
{
Node *left = pq.top(); pq.pop();
Node *right = pq.top(); pq.pop();
int sum = left->freq + right->freq;
pq.push(getNode('\0', sum, left, right));
}
Node* root = pq.top();
unordered_map<char, string> huffmanCode;
encode(root, "", huffmanCode);
cout << "Huffman Codes are :\n" << '\n';
for (auto pair: huffmanCode) {
cout << pair.first << " " << pair.second << '\n';
}
cout << "\nOriginal string was :\n" << text << '\n';
string str = "";
for (char ch: text) {
str += huffmanCode[ch];
}
cout << "\nEncoded string is :\n" << str << '\n';
int index = -1;
cout << "\nDecoded string is: \n";
while (index < (int)str.size() - 2) {
decode(root, index, str);
}
}
int main()
{
string text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
return 0;
}
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class Node
{
char ch;
int freq;
Node left = null, right = null;
Node(char ch, int freq)
{
this.ch = ch;
this.freq = freq;
}
public Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
};
class Huffman
{
public static void encode(Node root, String str,
Map<Character, String> huffmanCode)
{
if (root == null)
return;
if (root.left == null && root.right == null) {
huffmanCode.put(root.ch, str);
}
encode(root.left, str + "0", huffmanCode);
encode(root.right, str + "1", huffmanCode);
}
public static int decode(Node root, int index, StringBuilder sb)
{
if (root == null)
return index;
if (root.left == null && root.right == null)
{
System.out.print(root.ch);
return index;
}
index++;
if (sb.charAt(index) == '0')
index = decode(root.left, index, sb);
else
index = decode(root.right, index, sb);
return index;
}
public static void buildHuffmanTree(String text)
{
Map<Character, Integer> freq = new HashMap<>();
for (int i = 0 ; i < text.length(); i++) {
if (!freq.containsKey(text.charAt(i))) {
freq.put(text.charAt(i), 0);
}
freq.put(text.charAt(i), freq.get(text.charAt(i)) + 1);
}
PriorityQueue<Node> pq = new PriorityQueue<>(
(l, r) -> l.freq - r.freq);
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
pq.add(new Node(entry.getKey(), entry.getValue()));
}
while (pq.size() != 1)
{
Node left = pq.poll();
Node right = pq.poll();
int sum = left.freq + right.freq;
pq.add(new Node('\0', sum, left, right));
}
Node root = pq.peek();
Map<Character, String> huffmanCode = new HashMap<>();
encode(root, "", huffmanCode);
System.out.println("Huffman Codes are :\n");
for (Map.Entry<Character, String> entry : huffmanCode.entrySet()) {
System.out.println(entry.getKey() + " " + entry.getValue());
}
System.out.println("\nOriginal string was :\n" + text);
StringBuilder sb = new StringBuilder();
for (int i = 0 ; i < text.length(); i++) {
sb.append(huffmanCode.get(text.charAt(i)));
}
System.out.println("\nEncoded string is :\n" + sb);
int index = -1;
System.out.println("\nDecoded string is: \n");
while (index < sb.length() - 2) {
index = decode(root, index, sb);
}
}
public static void main(String[] args)
{
String text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
}
}
Nota: la memoria utilizada por la cadena de entrada es 47 * 8 = 376 bits, y la cadena codificada solo toma 194 bits, es decir los datos se comprimen en aproximadamente un 48%. En el programa C ++ anterior, usamos la clase de cadena para almacenar la cadena codificada para que el programa sea legible.Dado que las estructuras de datos efectivas de la cola de prioridad requieren tiempo O (log (N)) para insertarse, y en un árbol binario completo con N hojas hay 2N-1 nodos, y el árbol Huffman es un árbol binario completo, el algoritmo funciona para O (Nlog (N )) tiempo, donde N es el número de caracteres.Fuentes:
en.wikipedia.org/wiki/Huffman_codingen.wikipedia.org/wiki/Variable-length_codewww.youtube.com/watch?v=5wRPin4oxCo
.