¿Suena esto familiar: "Comencé a hacer desarrollo web después de tomar cursos"?Quizás desee mejorar su conocimiento de los conceptos básicos de la informática en términos de estructuras de datos y algoritmos. Hoy hablaremos sobre algunas de las estructuras de datos más comunes utilizando el ejemplo JS.1. Pila (llamadas) (Pila)
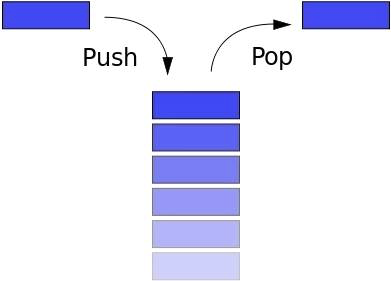La pila sigue el principio LIFO (último en entrar, primero en salir - último en entrar, primero en salir). Si apiló los libros uno encima del otro, y quería tomar el libro más bajo, primero tome el primero, luego el siguiente, etc. El botón "Atrás" en el navegador le permite ir (volver) a la página anterior.La pila tiene los siguientes métodos:- empujar: agregar nuevo elemento
- pop: eliminar el elemento superior, devolverlo
- vistazo: volver al elemento superior
- longitud: devuelve el número de elementos en la pila
Una matriz en JS tiene atributos de pila, pero la construiremos desde cero usando la función Stack ():function Stack() {
this.count = 0
this.storage = {}
this.push = function(value) {
this.storage[this.count] = value
this.count++
}
this.pop = function() {
if (this.count === 0) return undefined
this.count--
let result = this.storage[this.count]
delete this.storage[this.count]
return result
}
this.peek = function() {
return this.storage[this.count - 1]
}
this.size = function() {
return this.count
}
}
2. Cola (cola)
Una cola se asemeja a una pila. La diferencia es que la cola sigue el principio FIFO (Primero en entrar, primero en salir, primero en entrar, primero en salir). Cuando te paras en la fila, el primero siempre será el primero.La cola tiene los siguientes métodos:- en cola: ingrese la cola, agregue un elemento al final
- Dequeue: abandone la cola, elimine el primer elemento y devuélvalo
- frente: obtener el primer elemento
- isEmpty: verifica si la cola está vacía
- tamaño: obtenga el número de elementos en la cola
Una matriz en JS tiene algunos atributos de cola, por lo que podemos usarla para la demostración:function Queue() {
let collection = []
this.print = function() {
console.log(collection)
}
this.enqueue = function(element) {
collection.push(element)
}
this.dequeue = function() {
return collection.shift()
}
this.front = function() {
return collection[0]
}
this.isEmpty = function() {
return collection.length === 0
}
this.size = function() {
return collection.length
}
}
El orden de prioridad (prioridad)
La cola tiene una versión avanzada. Asigne una prioridad a cada elemento y los elementos se ordenarán en consecuencia:function PriorityQueue() {
...
this.enqueue = function(element) {
if (this.isEmpty()) {
collection.push(element)
} else {
let added = false
for (let i = 0; i < collection.length; i++) {
if (element[1] < collection[i][1]) {
collection.splice(i, 0, element)
added = true
break;
}
}
if (!added) {
collection.push(element)
}
}
}
}
Pruebas:let pQ = new PriorityQueue()
pQ.enqueue([gannicus, 3])
pQ.enqueue([spartacus, 1])
pQ.enqueue([crixus, 2])
pQ.enqueue([oenomaus, 4])
pQ.print()
Resultado:[
[spartacus, 1],
[crixus, 2],
[gannicus, 3],
[oenomaus, 4]
]
3. Una lista vinculada (lista vinculada de nodos y enlaces o punteros) (Lista vinculada)
Literalmente, una lista vinculada es una estructura de datos encadenada donde cada nodo consta de dos partes: datos de un nodo y un puntero al siguiente nodo. La lista vinculada y la matriz condicional son estructuras de datos lineales con almacenamiento serializado. Las diferencias son las siguientes:Una lista vinculada individualmente tiene los siguientes métodos:- tamaño: devuelve el número de nodos
- head: devuelve el primer elemento (head - head)
- add: agrega un elemento al final (tail - tail)
- eliminar: eliminar múltiples nodos
- indexOf: índice de nodo de retorno
- elementAt: devolver nodo por índice
- addAt: inserta un nodo en un lugar específico (por índice)
- removeAt: elimina un nodo específico (por índice)
function Node(element) {
this.element = element
this.next = null
}
function LinkedList() {
let length = 0
let head = null
this.size = function() {
return length
}
this.head = function() {
return head
}
this.add = function(element) {
let node = new Node(element)
if (head === null) {
head = node
} else {
let currentNode = head
while (currentNode.next) {
currentNode = currentNode.next
}
currentNode.next = node
}
length++
}
this.remove = function(element) {
let currentNode = head
let previousNode
if (currentNode.element !== element) {
head = currentNode.next
} else {
while (currentNode.element !== element) {
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
}
this.isEmpty = function() {
return length === 0
}
this.indexOf = function(element) {
let currentNode = head
let index = -1
while (currentNode) {
index++
if (currentNode.element === element) {
return index
}
currentNode = currentNode.next
}
return -1
}
this.elementAt = function(index) {
let currentNode = head
let count = 0
while (count < index) {
count++
currentNode = currentNode.next
}
return currentNode.element
}
this.addAt = function(index, element) {
let node = new Node(element)
let currentNode = head
let previousNode
let currentIndex = 0
if (index > length) return false
if (index === 0) {
node.next = currentNode
head = node
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
node.next = currentNode
previousNode.next = node
}
length++
}
this.removeAt = function(index) {
let currentNode = head
let previousNode
let currentIndex = 0
if (index < 0 || index >= length) return null
if (index === 0) {
head = currentIndex.next
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
return currentNode.element
}
}
4. Colección (de valores) (Conjunto)
Una colección (muchas) es uno de los conceptos básicos de las matemáticas: un conjunto de objetos bien definidos y aislados. ES6 introdujo una colección que tiene cierta semejanza con una matriz. Sin embargo, la colección no permite la inclusión de elementos duplicados y no contiene índices.La colección estándar tiene los siguientes métodos:- valores: devuelve todos los elementos de la colección
- tamaño: devuelve el número de elementos
- tiene: comprueba si un artículo está en la colección
- agregar: agregar elemento
- eliminar: eliminar un elemento
- union: devuelve el área de intersección de dos colecciones
- diferencia: devuelve las diferencias entre las dos colecciones
- subconjunto: verifique si una colección es un subconjunto de otra
function MySet() {
let collection = []
this.has = function(element) {
return (collection.indexOf(element) !== -1)
}
this.values = function() {
return collection
}
this.size = function() {
return collection.length
}
this.add = function(element) {
if (!this.has(element)) {
collection.push(element)
return true
}
return false
}
this.remove = function(element) {
if (this.has(element)) {
index = collection.indexOf(element)
collection.splice(index, 1)
return true
}
return false
}
this.union = function(otherSet) {
let unionSet = new MySet()
let firstSet = this.values()
let secondSet = otherSet.values()
firstSet.forEach(i => unionSet.add(i))
secondSet.forEach(i => unionSet.add(i))
}
this.intersection = function(otherSet) {
let intersectionSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (otherSet.has(e)) {
intersectionSet.add(e)
}
})
return intersectionSet
}
this.difference = function(otherSet) {
let differenceSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (!otherSet.has(e)) {
differenceSet.add(e)
}
})
return differenceSet
}
this.subset = function(otherSet) {
lat firstSet = this.values()
return firstSet.every(value => otherSet.has(value))
}
}
5. Tabla hash (tabla hash)
Una tabla hash es una estructura de datos que se construye sobre una base de valor clave. Debido a la alta velocidad de búsqueda de valores por clave, se utiliza en estructuras como Mapa, Diccionario y Objeto. Como se muestra en la figura, la tabla hash tiene una función hash que convierte las claves en una lista de números que se utilizan como los nombres (valores) de las claves. El tiempo de búsqueda del valor clave puede llegar a O (1). Las claves idénticas deben devolver el mismo valor: esta es la esencia de la función hash.Una tabla hash tiene los siguientes métodos:- add: agrega un par clave / valor
- eliminar: eliminar un par
- búsqueda: encontrar valor por clave
function hash(string, max) {
let hash = 0
for (let i = 0; i < string.length; i++) {
hash += string.charCodeAt(i)
}
return hash % max
}
function HashTable() {
let storage = []
const storageLimit = 4
this.add = function(key, value) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
storage[index] = [
[key, value]
]
} else {
let inserted = false
for (let i = 0; i < storage[index].len; i++) {
if (storage[index][i][0] === key) {
storage[index][i][1] = value
inserted = true
}
}
if (inserted === false) {
storage[index].push([key, value])
}
}
}
this.remove = function(key) {
let index = hash(key, storageLimit)
if (storage[index].length === 1 && storage[index][0][0] === key) {
delete storage[index]
} else {
for (let i = 0; i < storage[index]; i++) {
if (storage[index][i][0] === key) {
delete storage[index][i]
}
}
}
}
this.lookup = function(key) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
return undefined
} else {
for (let i = 0; i < storage[index].length; i++) {
if (storage[index][i][0] === key) {
return storage[index][i][1]
}
}
}
}
}
6. árbol
Una estructura de árbol es una estructura multicapa (multinivel). También es una estructura no lineal, a diferencia de una matriz, una pila y una cola. Esta estructura es muy efectiva en términos de agregar y buscar elementos. Aquí hay algunos conceptos de estructura de árbol:- root: elemento raíz, no tiene padre
- nodo principal: un nodo directo de la capa superior (nivel), solo puede haber uno
- nodo hijo: nodo (s) directo (s) del nivel inferior, puede haber varios
- hermanos: hijos de un nodo padre
- hoja: nudo sin "hijos"
- Borde: rama o enlace (enlace) entre nodos
- Ruta: ruta (conjunto de enlaces) desde el nodo de inicio al elemento de destino
- Altura del árbol: el número de enlaces de la ruta más larga desde un elemento específico a un nodo que no tiene hijos
- Profundidad del nodo: el número de enlaces desde el nodo raíz a un elemento específico.
- Grado de nodo: número de descendientes
Aquí hay un ejemplo de un árbol de búsqueda binario (BST). Cada nodo tiene solo dos descendientes, el nodo izquierdo (hijo) es más pequeño que el nodo actual (padre), el derecho es más grande: los
métodos de este árbol son los siguientes:- agregar: agregar nodo
- findMin: obtiene el nodo mínimo
- findMax: obtener el nodo máximo
- find: encuentra un nodo específico
- isPresent: busca un nodo específico
- eliminar: eliminar el nodo
class Node {
constructor(data, left = null, right = null) {
this.data = data
this.left = left
this.right = right
}
}
class BST {
constructor() {
this.root = null
}
add(data) {
const node = this.root
if (node === null) {
this.root = new Node(data)
return
} else {
const searchTree = function(node) {
if (data < node.data) {
if (node.left === null) {
node.left = new Node(data)
return
} else if (node.left !== null) {
return searchTree(node.left)
}
} else if (data > node.data) {
if (node.right === null) {
node.right = new Node(data)
return
} else if (node.right !== null) {
return searchTree(node.right)
}
} else {
return null
}
}
return searchTree(node)
}
}
findMin() {
let current = this.root
while (current.left !== null) {
current = current.left
}
return current.data
}
findMax() {
let current = this.root
while (current.right !== null) {
current = current.right
}
return current.data
}
find(data) {
let current = this.root
while (current.data !== data) {
if (data < current.data) {
current = current.left
} else {
current = current.right
}
if (current === null) {
return null
}
}
return current
}
isPresent(data) {
let current = this.root
while (current) {
if (data === current.data) {
return true
}
data < current.data ? current = current.left : current = current.right
}
return false
}
remove(data) {
const removeNode = function(node, data) {
if (node === null) return null
if (data === node.data) {
if (node.left === null && node.right === null) return null
if (node.left === null) return node.right
if (node.right === null) return node.left
let tempNode = node.right
while (tempNode.left !== null) {
tempNode = tempNode.left
}
node.data = tempNode.data
node.right = removeNode(node.right, tempNode.data)
return node
} else if (data < node.data) {
node.left = removeNode(node.right, data)
return node
} else {
node.right = removeNode(node.right, data)
return node
}
}
this.root = removeNode(this.root, data)
}
}
Pruebas:const bst = new BST()
bst.add(4)
bst.add(2)
bst.add(6)
bst.add(1)
bst.add(3)
bst.add(5)
bst.add(7)
bst.remove(4)
console.log(bst.findMin())
console.log(bst.findMax())
bst.remove(7)
console.log(bst.findMax())
console.log(bst.isPresent(4))
Resultado:1
7
6
false
7. Árbol cargado (prefijo) (Trie, leído como "probar")
El árbol de prefijos es un tipo de árbol de búsqueda. Los datos que contiene se almacenan secuencialmente (paso a paso): cada nodo de árbol representa un paso. El árbol de prefijos se usa en los diccionarios, ya que acelera significativamente la búsqueda.Cada nodo de árbol es una letra del alfabeto, y una rama lleva a la formación de una palabra. También contiene un "indicador booleano" para determinar que el nodo actual es la última letra.El árbol de prefijos tiene los siguientes métodos:- add: agrega una palabra al diccionario
- isWord: busca una palabra
- print: devuelve todas las palabras
function Node() {
this.keys = new Map()
this.end = false
this.setEnd = function() {
this.end = true
}
this.isEnd = function() {
return this.end
}
}
function Trie() {
this.root = new Node()
this.add = function(input, node = this.root) {
if (input.length === 0) {
node.setEnd()
return
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node())
return this.add(input.substr(1), node.key.get(input[0]))
} else {
return this.add(input.substr(1), node.keys.get(input[0]))
}
}
this.isWord = function(word) {
let node = this.root
while (word.length > 1) {
if (node.keys.has(word[0])) {
return false
} else {
node = node.keys.get(word[0])
word = word.substr(1)
}
}
return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false
}
this.print = function() {
let words = new Array()
let search = function(node = this.root, string) {
if (node.keys.size !== 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter))
}
if (node.isEnd()) {
words.push(string)
}
} else {
string.length > 0 ? words.push(string) : undefined
return
}
}
search(this.root, new String())
return words.length > 0 ? words : null
}
}
8. El gráfico (gráfico) (Gráfico)
Un gráfico, también conocido como Red, es una colección de nodos interconectados. Hay dos tipos de gráficos: orientados y no orientados, dependiendo de si los enlaces tienen una dirección. Los gráficos se usan en todas partes, por ejemplo, para calcular la mejor ruta en aplicaciones de navegación o para crear una lista de recomendaciones en las redes sociales.Los gráficos se pueden presentar en forma de lista o matriz.Lista
En este caso, todos los nodos principales se encuentran a la izquierda y sus hijos a la derecha.
La matriz
En este caso, los nodos se distribuyen en filas y columnas, la intersección de la fila y la columna muestra la relación entre los nodos: 0 significa que los nodos no están conectados, 1 - los nodos están conectados.
El gráfico se busca por dos métodos: búsqueda por amplitud (Breath-First-Search, BFS) y búsqueda por profundidad (Depth-First-Search, DFS).Considere BFS:function bfs(graph, root) {
let nodesLen = {}
for (let i = 0; i < graph.length; i++) {
nodesLen[i] = Infinity
}
nodesLen[root] = 0
let queue = [root]
let current
while (queue.length !== 0) {
current = queue.shift()
let curConnected = graph[current]
let neighborIdx = []
let idx = curConnected.indexOf(1)
while (idx !== -1) {
neighborIdx.push(idx)
idx = curConnected.indexOf(1, idx + 1)
}
for (let i = 0; i < neighborIdx.length; i++) {
if (nodesLen[neighborIdx[i]] === Infinity) {
nodesLen[neighborIdx[i]] = nodesLen[current] + 1
queue.push(neighborIdx[i])
}
}
}
return nodesLen
}
Pruebas:let graph = [
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 0, 0]
]
console.log(bfs(graph, 1))
Resultado:{
0: 2,
1: 0,
2: 1,
3: 3,
4: Infinity
}
Eso es todo para mí. Espero que encuentres algo útil para ti. ¡Feliz codificación!