F #, algoritmo de marcado para componentes de imagen conectados

La búsqueda y el marcado de componentes conectados en imágenes binarias es uno de los algoritmos básicos para el análisis y procesamiento de imágenes. En particular, este algoritmo se puede utilizar en visión artificial para buscar y contar estructuras comunes en la imagen, con su posterior análisis.

En el marco de este artículo, se considerarán dos algoritmos para marcar componentes conectados, se muestra su implementación en el lenguaje de programación F #. Y también, un análisis comparativo de los algoritmos, la búsqueda de debilidades. El material fuente para la implementación de los algoritmos fue tomado del libro " Computer Vision" (autores L. Shapiro, J. Stockman. Traducción del inglés por A. A. Boguslavsky editado por S. M. Sokolov) .

Introducción

Un componente conectado con un valor de v es un conjunto de C tales píxeles que tienen un valor de v y cada par de estos píxeles está conectado con un valor de v

Suena abstruso, así que veamos la imagen. Suponemos que los píxeles de primer plano de la imagen binaria están marcados como 1 , y los píxeles de fondo están marcados como 0 .

Después de procesar la imagen con el algoritmo de marcado de los componentes conectados, obtenemos la siguiente imagen. Aquí, en lugar de píxeles, se forman componentes conectados, que difieren entre sí en número. En este ejemplo, se encontraron 5 componentes y será posible trabajar con ellos como con entidades separadas.

Figura 1: Componentes conectados etiquetados

$$

$$\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 2 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 2 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 \\ 3 & 3 & 3 & 3 & 0 & 4 & 0 & 2 \\ 0 & 0 & 0 & 3 & 0 & 4 & 0 & 2 \\ 5 & 5 & 0 & 3 & 0 & 0 & 0 & 2 \\ 5 & 5 & 0 & 3 & 0 & 2 & 2 & 2 \end{matrix}$$

A continuación se considerarán dos algoritmos que se pueden usar para resolver dicho problema.

Algoritmo de etiquetado recursivo

Comenzaremos mirando el algoritmo basado en la recursividad como el más obvio. El principio de funcionamiento de dicho algoritmo será el siguiente:

Asigne una etiqueta, que marcará los componentes relacionados, el valor inicial.

1. Ordenamos todos los puntos de la tabla, comenzando con la coordenada 0x0 (esquina superior izquierda). Después de procesar el siguiente punto, aumente la etiqueta en uno
2. Si el píxel en la coordenada actual es 1 , entonces escaneamos los cuatro vecinos de este punto (arriba, abajo, derecha, izquierda)
3. Si el punto vecino también es 1 , entonces la función se llama recursivamente para procesar al vecino hasta que alcanza el límite de la matriz o el punto 0
4. Durante el procesamiento recursivo del vecino, se debe verificar que el punto no haya sido procesado y que esté marcado con el marcador actual.

Por lo tanto, clasificando todos los puntos en la matriz e invocando un algoritmo recursivo para cada uno, luego al final de la búsqueda obtenemos una tabla completamente marcada. Como hay una comprobación de si un punto dado ya ha sido marcado, cada punto se procesará solo una vez. La profundidad de recursión dependerá solo del número de vecinos conectados al punto actual. Este algoritmo es muy adecuado para imágenes que no tienen un relleno de imagen grande. Es decir, imágenes en las que hay líneas finas y cortas, y todo lo demás es una imagen de fondo que no se procesa. Además, la velocidad de dicho algoritmo puede ser mayor que el algoritmo línea por línea (lo discutiremos más adelante en el artículo).

Dado que las imágenes binarias bidimensionales son matrices bidimensionales, al escribir el algoritmo, operaré con los conceptos de matrices, sobre los cuales hice un artículo separado, que se puede leer aquí.

Programación funcional usando el ejemplo de trabajar con matrices de la teoría del álgebra lineal.

Consideremos y analicemos en detalle la función F # que implementa algoritmo de etiquetado recursivo para componentes de imágenes binarias conectadas

let recMarkingOfConnectedComponents matrix =

        let copy = Matrix.clone matrix

        let (|Value|Zero|Out|) (x, y) = 
            if x < 0 || y < 0
                || x > (copy.values.[0, *].Length - 1)
                || y > (copy.values.[*, 0].Length - 1) then
                Out
            else
                let row = copy.values.[y, *]
                match row.[x] with
                    | 0 -> Zero
                    | v -> Value(v)

        let rec markBits x y value =
            match (x, y) with
            | Value(v) ->
                if value > v then
                    copy.values.[y, x] <- value
                    markBits (x + 1) y value
                    markBits (x - 1) y value
                    markBits x (y + 1) value
                    markBits x (y - 1) value
            | Zero | Out -> ()

        let mutable value = 2
        copy.values
        |> Array2D.iteri (fun y x v -> if v = 1 then
                                            markBits x y value
                                            value <- value + 1)

        copy 

Declaramos la función recMarkingOfConnectedComponents , que toma una matriz bidimensional de matriz, empaquetada en un registro de tipo Matrix. La función no cambiará la matriz original, así que primero cree una copia de la misma, que será procesada por el algoritmo y devuelta.

let copy = Matrix.clone matrix

Para simplificar las comprobaciones de los índices de los puntos solicitados fuera de la matriz, cree una plantilla activa que devuelva uno de los tres valores.

Fuera : el índice solicitado fue más allá de la matriz bidimensional
Cero : el punto contiene un píxel de fondo (igual a cero)
Valor : el índice solicitado está dentro de la matriz

Esta plantilla simplificará la comprobación de las coordenadas del punto de imagen en el siguiente cuadro de recursión:

let (|Value|Zero|Out|) (x, y) = 
    if x < 0 || y < 0
        || x > (copy.values.[0, *].Length - 1)
        || y > (copy.values.[*, 0].Length - 1) then
        Out
    else
        let row = copy.values.[y, *]
        match row.[x] with
            | 0 -> Zero
            | v -> Value(v)

La función MarkBits se declara recursiva y sirve para procesar el píxel actual y todos sus vecinos (arriba, abajo, izquierda, derecha):

let rec markBits x y value =
    match (x, y) with
    | Value(v) ->
        if value > v then
            copy.values.[y, x] <- value
            markBits (x + 1) y value
            markBits (x - 1) y value
            markBits x (y + 1) value
            markBits x (y - 1) value
    | Zero | Out -> ()

La función acepta los siguientes parámetros como entrada:

x - número de fila
y -
valor de número de columna - valor de etiqueta actual para marcar el píxel.

Usando la construcción match / with y la plantilla activa (arriba), las coordenadas de los píxeles se verifican para que no vaya más allá de las dos dimensiones formación. Si el punto está dentro de una matriz bidimensional, entonces hacemos una verificación preliminar para no procesar el punto que ya ha sido procesado.

if value > v then

De lo contrario, se producirá una recursión infinita y el algoritmo no funcionará.

A continuación, marque el punto con el valor del marcador actual:

copy.values.[y, x] <- value

Y procesamos todos sus vecinos, invocando recursivamente la misma función:

markBits (x + 1) y value
markBits (x - 1) y value
markBits x (y + 1) value
markBits x (y - 1) value

Después de implementar el algoritmo, debe usarse. Considere el código con más detalle.

let mutable value = 2
copy.values
|> Array2D.iteri (fun y x v -> if v = 1 then
                                    markBits x y value
                                    value <- value + 1) 

Antes de procesar la imagen, establezca el valor inicial de la etiqueta, que marcará los grupos de píxeles conectados.

let mutable value = 2

El hecho es que los píxeles frontales en la imagen binaria ya están establecidos en 1 , por lo que si el valor inicial de la etiqueta también es 1 , entonces el algoritmo no funcionará. Por lo tanto, el valor inicial de la etiqueta debe ser mayor que 1 . Hay otra forma de resolver el problema. Antes de comenzar el algoritmo, marque todos los píxeles establecidos en 1 con un valor inicial de -1 . Entonces podemos establecer el valor en 1 . Puede hacerlo usted mismo si lo desea.

La siguiente construcción, utilizando la función Array2D.iteri , itera sobre todos los puntos de la matriz, y si durante la búsqueda encuentra un punto establecido en 1, esto significa que no se procesa y para ello debe llamar a la función recursiva markBits con el valor de etiqueta actual. El algoritmo ignora todos los píxeles establecidos en 0 .

Después de procesar recursivamente el punto, podemos suponer que se garantiza que se marcará todo el grupo conectado al que pertenece este punto y puede aumentar el valor de la etiqueta en 1 para aplicarlo al siguiente punto conectado.

Considere un ejemplo de la aplicación de dicho algoritmo.

let a = array2D [[1;1;0;1;1;1;0;1]
                 [1;1;0;1;0;1;0;1]
                 [1;1;1;1;0;0;0;1]
                 [0;0;0;0;0;0;0;1]
                 [1;1;1;1;0;1;0;1]
                 [0;0;0;1;0;1;0;1]
                 [1;1;0;1;0;0;0;1]
                 [1;1;0;1;0;1;1;1]]
let A = Matrix.ofArray2D a

let t = System.Diagnostics.Stopwatch.StartNew()
let R = Algorithms.recMarkingOfConnectedComponents A
t.Stop()

printfn "origin =\n %A" A.values
printfn "rec markers =\n %A" R.values
printfn "elapsed recurcive = %O" t.Elapsed 

origin =
 [[1; 1; 0; 1; 1; 1; 0; 1]
 [1; 1; 0; 1; 0; 1; 0; 1]
 [1; 1; 1; 1; 0; 0; 0; 1]
 [0; 0; 0; 0; 0; 0; 0; 1]
 [1; 1; 1; 1; 0; 1; 0; 1]
 [0; 0; 0; 1; 0; 1; 0; 1]
 [1; 1; 0; 1; 0; 0; 0; 1]
 [1; 1; 0; 1; 0; 1; 1; 1]]

rec markers =
 [[2; 2; 0; 2; 2; 2; 0; 3]
 [2; 2; 0; 2; 0; 2; 0; 3]
 [2; 2; 2; 2; 0; 0; 0; 3]
 [0; 0; 0; 0; 0; 0; 0; 3]
 [4; 4; 4; 4; 0; 5; 0; 3]
 [0; 0; 0; 4; 0; 5; 0; 3]
 [6; 6; 0; 4; 0; 0; 0; 3]
 [6; 6; 0; 4; 0; 3; 3; 3]]

elapsed recurcive = 00:00:00.0037342

Las ventajas de un algoritmo recursivo incluyen su simplicidad en la escritura y la comprensión. Es ideal para imágenes binarias que contienen un gran fondo y se intercalan con pequeños grupos de píxeles (por ejemplo, líneas, pequeños puntos, etc.). En este caso, la velocidad de procesamiento de la imagen puede ser alta, ya que el algoritmo procesa la imagen completa de una sola vez.

Las desventajas también son obvias: esto es recurrencia. Si la imagen consta de puntos grandes o está completamente inundada, entonces la velocidad de procesamiento cae bruscamente (por órdenes de magnitud) y existe el riesgo de que el programa se bloquee debido a la falta de espacio libre en la pila.

Desafortunadamente, el principio de recursión de cola no se puede aplicar en este algoritmo, porque la recursión de cola tiene dos requisitos:

1. Cada cuadro de recursión debe realizar cálculos y agregar el resultado al acumulador, que se transmitirá por la pila.
2. No debe haber más de una llamada de función recursiva en un marco de recursión.

En nuestro caso, la recursión no realiza ningún cálculo final, que se puede pasar al siguiente cuadro de recursión, sino que simplemente modifica una matriz bidimensional. En principio, esto podría evitarse simplemente devolviendo un solo número, lo que en sí mismo no significa nada. También hacemos 4 llamadas de forma recursiva, ya que necesitamos procesar a los cuatro vecinos del punto.

Algoritmo clásico para marcar componentes conectados según la estructura de datos para combinar búsquedas

El algoritmo también tiene otro nombre, "Algoritmo de marcado progresivo", y aquí intentaremos analizarlo.

. . . , , .

La definición anterior es aún más confusa, por lo que trataremos de tratar el principio del algoritmo de una manera diferente y comenzar desde lejos.

Primero, trataremos la definición de un vecindario de cuatro puntos conectados y ocho puntos conectados del punto actual. Mire las imágenes a continuación para comprender qué es y cuál es la diferencia.

Figura 2: El componente de cuatro conexiones
\ begin {matrix} Figura 2: El componente de ocho conexiones \ begin {matrix} La primera imagen muestra un componente de cuatro conectados $$\begin{matrix} & 1 & \\ 2 & * & 3 \\ & 4 & \end{matrix}$$


$$\begin{matrix} 1 & 2 & 3 \\ 4 & * & 5 \\ 6 & 7 & 8 \end{matrix}$$
puntos, es decir, esto significa que el algoritmo procesa 4 vecinos del punto actual (izquierda, derecha, arriba y abajo). En consecuencia, el componente de un punto conectado a ocho significa que tiene 8 vecinos. En este artículo, trabajaremos con cuatro componentes conectados.

Ahora necesita averiguar qué es una estructura de datos para combinar la búsqueda , construida en algunos conjuntos.

Por ejemplo, supongamos que tenemos dos conjuntos

$$

$$(1, 2, 3, 4, 8) (5, 6, 7)$$

Estos conjuntos están organizados en la forma de los siguientes árboles: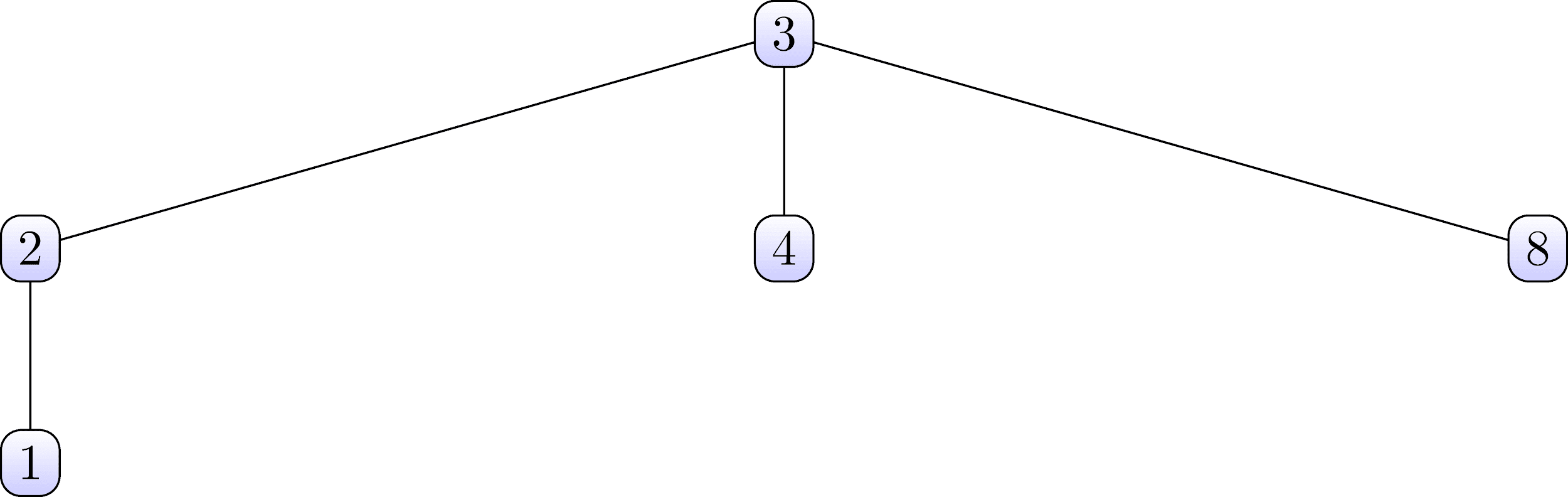





Tenga en cuenta que en el primer conjunto, los nodos 3 son raíz, y en el segundo, nodos 6.

Ahora consideramos la estructura de datos para una unión de búsqueda, que contiene ambos conjuntos, y también organiza su estructura de árbol .

Figura 4: Estructura de datos para búsqueda-unión
\ begin {matrix} Mire cuidadosamente la tabla de arriba e intente encontrar una relación con los árboles de conjunto que se muestran arriba. La tabla debe verse en columnas verticales. Se observa,que el número 3 en la primera línea corresponde al número 0 $$\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 2 & 3 & 0 & 3 & 7 & 7 & 0 & 3 \end{matrix}$$

en la segunda linea. Y en el primer árbol, el número 3 es la raíz del primer conjunto. Por analogía, puede encontrar que el número 7 de la primera línea corresponde al número 0 de la segunda línea. El número 7 también es la raíz del árbol del segundo conjunto.

Por lo tanto, concluimos que los números de la fila superior son los nodos secundarios de los conjuntos, y los números correspondientes de la fila inferior son sus nodos principales. Guiado por esta regla, puede restaurar fácilmente ambos árboles de la tabla anterior.

Analizamos dichos detalles para que luego nos sea más fácil entender cómo funciona el algoritmo de marcado progresivo .. Por ahora, detengámonos en el hecho de que una serie de números de la primera fila siempre son números del 1 a un cierto número máximo. De hecho, el número máximo de la primera fila es el valor máximo de las etiquetas con las que se marcarán los componentes conectados encontrados . Y los conjuntos individuales son transiciones entre etiquetas que se forman como resultado del primer paso (lo consideraremos con más detalle más adelante).

Antes de continuar, considere el pseudocódigo de algunas funciones que utilizará el algoritmo.

Denotamos la tabla que representa la estructura de datos para la búsqueda conjunta como PADRE . La siguiente función se llama buscar y tomará la etiqueta X actual como parámetrosy una gran variedad de PADRES . Este procedimiento padres rastros punteros hasta la raíz del árbol y encuentra la etiqueta del nodo raíz del árbol a la que X pertenece .

 ̆   ̆  .
X —  
PARENT — , ̆    -

procedure find(X, PARENT);
{
j := X;
while PARENT[j] <> 0
    j := PARENT[j]; return(j);
}

Considere cómo se puede implementar dicha función en F #

let rec find x =
    let index = Array.tryFindIndex ((=)x) parents.[0, *]
    match index with
    | Some(i) -> 
        match parents.[1, i] with
        | p when p <> 0 -> find p
        | _ -> x
    | None -> x 

Aquí declaramos una función recursiva del hallazgo , que lleva la etiqueta actual en la X . La matriz PARRENT no se pasa aquí, ya que la tenemos en el espacio de nombres global y la función ya la ve y puede trabajar con ella.

Primero, la función intenta encontrar el índice de la etiqueta en la línea superior (ya que necesita encontrar su padre, que se encuentra en la línea inferior).

let index = Array.tryFindIndex ((=)x) parents.[0, *]

Si la búsqueda tiene éxito, entonces obtenemos su padre y lo comparamos con 0 . Si el padre no es igual a 0 , entonces este nodo también tiene un padre, y la función se llama recursivamente hasta que el padre es igual a 0 . Esto significará que hemos encontrado el nodo raíz del conjunto.

match index with
    | Some(i) -> 
        match parents.[1, i] with
        | p when p <> 0 -> find p
        | _ -> x
    | None -> x 

La siguiente función que necesitamos se llama unión . Se necesitan dos etiquetas X e Y , así como una matriz de PADRES . Esta estructura modifica (si es necesario) PADRE subconjunto de fusión que contiene una etiqueta de X , con el conjunto que comprende la etiqueta Y . El procedimiento busca los nodos raíz de ambas etiquetas y, si no coinciden, el nodo de una de las etiquetas se designa como el nodo principal de la segunda etiqueta. Entonces hay una unión de dos conjuntos.

   .
X — ,   .
Y — ,   .
PARENT — , ̆    -.

procedure union(X, Y, PARENT);
{
j := X;
k := Y;
while PARENT[j] <> 0
    j := PARENT[j];
while PARENT[k]] <> 0
    k := PARENT[k];

if j <> k then PARENT[k] := j;
} 

La implementación de F # se ve así

let union x y =
    let j = find x
    let k = find y
    if j <> k then parents.[1, k-1] <- j 

Tenga en cuenta que la función de búsqueda que ya hemos implementado ya se usa aquí .

El algoritmo también requiere dos funciones adicionales, que se denominan vecinos y etiquetas . La función de vecinos devuelve el conjunto de puntos vecinos a la izquierda y la parte superior (ya que en nuestro caso el algoritmo funciona en un componente conectado a cuatro) desde el píxel dado, y la función de etiquetas devuelve el conjunto de etiquetas que ya estaban asignadas al conjunto de píxeles dado que la función de vecinos devolvió . En nuestro caso, no implementaremos estas dos funciones, pero crearemos solo una que combine ambas funciones y devuelva las etiquetas encontradas.

let neighbors_labels x y =
    match (x, y) with
    | (0, 0) -> []
    | (0, _) -> [step1.[0, y-1]]
    | (_, 0) -> [step1.[x-1, 0]]
    | _ -> [step1.[x, y-1]; step1.[x-1, y]]
    |> List.filter ((<>)0) 

Mirando hacia el futuro, diré de inmediato que la matriz paso1 que usa la función ya existe en el espacio global y contiene el resultado del procesamiento del algoritmo en el primer paso. Quiero prestar especial atención al filtro adicional.

|> List.filter ((<>)0)

Corta todos los resultados que son 0 . Es decir, si la etiqueta contiene 0 , entonces estamos tratando con un punto en la imagen de fondo que no necesita ser procesado. Este es un matiz muy importante que no se menciona en el libro, del cual tomamos ejemplos, pero sin embargo, el algoritmo no funcionará sin dicha verificación.

Poco a poco, paso a paso, nos acercamos a la esencia misma del algoritmo. Veamos nuevamente la imagen que necesitaremos procesar.

Figura 5: Imagen binaria original
\ begin {matrix} $$\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 & 1 & 1 \end{matrix}$$

Antes de procesar, cree una matriz vacía step1 , en la que se guardará el resultado de la primera pasada.

Figura 6: Paso 1 de la matriz para almacenar los resultados del procesamiento primario
\ begin {matrix} $$\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

Considere los primeros pasos del procesamiento de datos primarios (solo las primeras tres líneas de la imagen binaria original).

Antes de analizar paso a paso el algoritmo, veamos el pseudocódigo que explica el principio general de funcionamiento.

     .
B —   .
LB —   .

procedure classical_with_union-find(B, LB);
{
“  .” initialize();
“  1 ̆  L     .”
for L := 0 to MaxRow
{
“     L  ”
for P := 0 to MaxCol
    LB[L,P] := 0;
“  L.”
for P := 0 to MaxCol
    if B[L,P] == 1 then
    {
        A := prior_neighbors(L,P);
        if isempty(A)
        then {M := label; label := label + 1;};
        else M := min(labels(A));
        LB[L,P] := M;
        for X in labels(A) and X <> M
           union(M, X, PARENT);
    }
}
“  2 ,    1,     .”
for L := 0 to MaxRow
    for P := 0 to MaxCol
        if B[L, P] == 1
        then LB[L,P] := find(LB[L,P], PARENT);
};
      LB ( step1)     ( ).

Figura 7: Paso 1. Punto (0,0), etiqueta = 1
\ begin {matrix} Figura 8: Paso 2. Punto (1,0), etiqueta = 1 \ begin {matrix} Figura 9: Paso 2. Punto (2,0), etiqueta = 1 \ begin {matrix} Figura 10: Paso 4. Punto (3.0), etiqueta = 2 \ begin {matrix} $$\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

$$\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

$$\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$

$$\begin{matrix} 1 & 1 & 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}$$
Figura 11: Último paso, resultado final de la primera pasada
\ comenzar { matriz} Tenga en cuenta que como resultado del procesamiento inicial de la imagen original, obtuvimos dos conjuntos $$\begin{matrix} 1 & 1 & 0 & 2 & 2 & 2 & 0 & 3 \\ 1 & 1 & 0 & 2 & 0 & 2 & 0 & 3 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\ 4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\ 0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 7 & 7 & 3 \end{matrix}$$

$$

$$(1,2) - (3,7)$$

Visualmente, esto puede verse como el contacto de las marcas 1 y 2 (coordenadas de los puntos (1,3) y (2,3) ) y las marcas 3 y 7 (coordenadas de los puntos (7,7) y (7,6) ). Desde el punto de vista de la estructura de datos para búsqueda-unión, se obtiene este resultado.

Figura 12: La estructura de datos calculada para unirse a la búsqueda
\ begin {matrix} Después finalmente procesamiento de imágenes utilizando la estructura de datos obtenida, obtenemos el siguiente resultado. Figura 13:Resultado final \ begin {matrix} $$\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 0 & 1 & 0 & 0 & 0 & 0 & 3 \end{matrix}$$



$$\begin{matrix} 1 & 1 & 0 & 1 & 1 & 1 & 0 & 3 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 3 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 \\ 4 & 4 & 4 & 4 & 0 & 5 & 0 & 3 \\ 0 & 0 & 0 & 4 & 0 & 5 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 0 & 0 & 3 \\ 6 & 6 & 0 & 4 & 0 & 3 & 3 & 3 \end{matrix}$$
Ahora todos los componentes conectados que tenemos tienen etiquetas únicas y sus se puede usar en algoritmos posteriores para el procesamiento.

La implementación del código F # es la siguiente

let markingOfConnectedComponents matrix =

    // up to 10 markers
    let parents = Array2D.init 2 10 (fun x y -> if x = 0 then y+1 else 0)

    // create a zero initialized copy
    let step1 = (Matrix.cloneO matrix).values

    let rec find x =
        let index = Array.tryFindIndex ((=)x) parents.[0, *]
        match index with
        | Some(i) -> 
            match parents.[1, i] with
            | p when p <> 0 -> find p
            | _ -> x
        | None -> x

    let union x y =
        let j = find x
        let k = find y
        if j <> k then parents.[1, k-1] <- j

    // returns up and left neighbors of pixel
    let neighbors_labels x y =
        match (x, y) with
        | (0, 0) -> []
        | (0, _) -> [step1.[0, y-1]]
        | (_, 0) -> [step1.[x-1, 0]]
        | _ -> [step1.[x, y-1]; step1.[x-1, y]]
        |> List.filter ((<>)0)

    let mutable label = 0
    matrix.values
    |> Array2D.iteri (fun x y v ->
                        if v = 1 then
                            let n = neighbors_labels x y
                            let m = if n.IsEmpty then
                                        label <- label + 1
                                        label
                                    else
                                        n |> List.min
                            n |> List.iter (fun v -> if v <> m then union m v)
                            step1.[x, y] <- m)

    let step2 = matrix.values
                |> Array2D.mapi (fun x y v ->
                        if v = 1 then step1.[x, y] <- find step1.[x, y]
                        step1.[x, y])

    { values = step2 } 

Una explicación línea por línea del código ya no tiene sentido, ya que todo se describió anteriormente. Aquí puede simplemente asignar el código F # al pseudocódigo para dejar en claro cómo funciona.

Algoritmos de evaluación comparativa

Comparemos la velocidad de procesamiento de datos con ambos algoritmos (recursivo y en fila).

let a = array2D [[1;1;0;1;1;1;0;1]
                 [1;1;0;1;0;1;0;1]
                 [1;1;1;1;0;0;0;1]
                 [0;0;0;0;0;0;0;1]
                 [1;1;1;1;0;1;0;1]
                 [0;0;0;1;0;1;0;1]
                 [1;1;0;1;0;0;0;1]
                 [1;1;0;1;0;1;1;1]]
let A = Matrix.ofArray2D a

let t1 = System.Diagnostics.Stopwatch.StartNew()
let R1 = Algorithms.markingOfConnectedComponents A
t1.Stop()

let t2 = System.Diagnostics.Stopwatch.StartNew()
let R2 = Algorithms.recMarkingOfConnectedComponents A
t2.Stop()

printfn "origin =\n %A" A.values
printfn "markers =\n %A" R1.values
printfn "rec markers =\n %A" R2.values

printfn "elapsed lines = %O" t1.Elapsed
printfn "elapsed recurcive = %O" t2.Elapsed 

origin =
 [[1; 1; 0; 1; 1; 1; 0; 1]
 [1; 1; 0; 1; 0; 1; 0; 1]
 [1; 1; 1; 1; 0; 0; 0; 1]
 [0; 0; 0; 0; 0; 0; 0; 1]
 [1; 1; 1; 1; 0; 1; 0; 1]
 [0; 0; 0; 1; 0; 1; 0; 1]
 [1; 1; 0; 1; 0; 0; 0; 1]
 [1; 1; 0; 1; 0; 1; 1; 1]]
markers =
 [[1; 1; 0; 1; 1; 1; 0; 3]
 [1; 1; 0; 1; 0; 1; 0; 3]
 [1; 1; 1; 1; 0; 0; 0; 3]
 [0; 0; 0; 0; 0; 0; 0; 3]
 [4; 4; 4; 4; 0; 5; 0; 3]
 [0; 0; 0; 4; 0; 5; 0; 3]
 [6; 6; 0; 4; 0; 0; 0; 3]
 [6; 6; 0; 4; 0; 3; 3; 3]]
rec markers =
 [[2; 2; 0; 2; 2; 2; 0; 3]
 [2; 2; 0; 2; 0; 2; 0; 3]
 [2; 2; 2; 2; 0; 0; 0; 3]
 [0; 0; 0; 0; 0; 0; 0; 3]
 [4; 4; 4; 4; 0; 5; 0; 3]
 [0; 0; 0; 4; 0; 5; 0; 3]
 [6; 6; 0; 4; 0; 0; 0; 3]
 [6; 6; 0; 4; 0; 3; 3; 3]]
elapsed lines = 00:00:00.0081837
elapsed recurcive = 00:00:00.0038338

Como puede ver, en este ejemplo, la velocidad del algoritmo recursivo excede significativamente la velocidad del algoritmo línea por línea. Pero todo cambia tan pronto como comencemos a procesar una imagen llena de color sólido y, para mayor claridad, también aumentaremos su tamaño a 100x100 píxeles.

let a = Array2D.create 100 100 1
let A = Matrix.ofArray2D a

let t1 = System.Diagnostics.Stopwatch.StartNew()
let R1 = Algorithms.markingOfConnectedComponents A
t1.Stop()
printfn "elapsed lines = %O" t1.Elapsed

let t2 = System.Diagnostics.Stopwatch.StartNew()
let R2 = Algorithms.recMarkingOfConnectedComponents A
t2.Stop()
printfn "elapsed recurcive = %O" t2.Elapsed 

elapsed lines = 00:00:00.0131790
elapsed recurcive = 00:00:00.2632489

Como puede ver, el algoritmo recursivo ya es 25 veces más lento que el lineal. Aumentemos el tamaño de la imagen a 200x200 píxeles.

elapsed lines = 00:00:00.0269896
elapsed recurcive = 00:00:06.1033132

La diferencia ya es muchos cientos de veces. Observo que ya en un tamaño de 300x300 píxeles, el algoritmo recursivo provoca un desbordamiento de la pila y el programa se bloquea.

Resumen

En el marco de este artículo, se consideró uno de los algoritmos básicos para marcar componentes conectados para procesar imágenes binarias usando el lenguaje funcional F # como ejemplo. Aquí se dieron ejemplos de la implementación de algoritmos recursivos y clásicos, se explicó su principio de funcionamiento, se realizó un análisis comparativo utilizando ejemplos específicos.

El código fuente discutido aquí también se puede ver en el github
MatrixAlgorithms.

Espero que este artículo sea interesante para aquellos interesados ​​en F # y en los algoritmos de procesamiento de imágenes en particular.