🛎️ 👩🏿‍⚖️ 💪🏿 Julia y la computación cuántica 🏄 🦂 ☄️

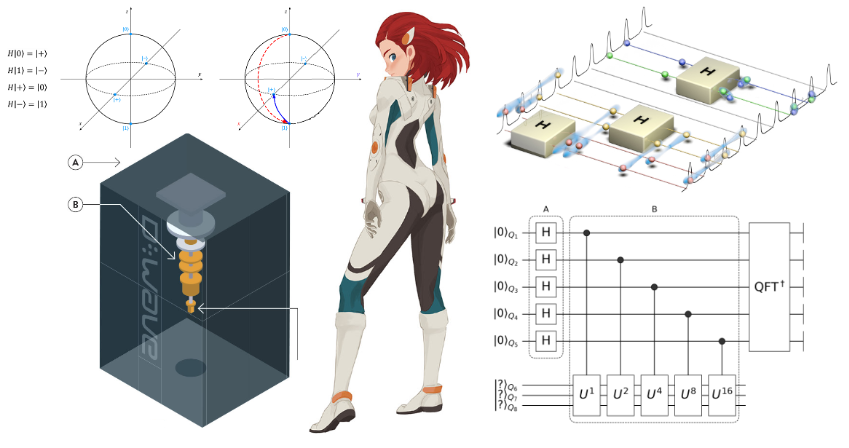
Presentamos Yao ( artículo ), un paquete de código abierto de Julia para resolver problemas prácticos en la investigación de computación cuántica. El nombre Yao proviene del primer carácter chino que significa unitaridad (幺正).

Yao? , , , Julia. , :

Julia ( Zygote), , , . , , .. , !

(AD) : - . AD , – , .

Yao - (AD), . . AD

n, d = 16, 100
circuit = dispatch!(variational_circuit(n, d),:random);
h = heisenberg(n)

@time for i in 1:100
     _, grad = expect'(h, zero_state(n) => circuit)
     dispatch!(-, circuit, 1e-1 * grad)
     println("Step $i, energy = $(real.(expect(h, zero_state(n)=>circuit)))")
end

100- (4816 ), 16- . AD , Zygote, (). , . .

. . , , .

-, - ( , QBIR) . Yao , , . , , , CUDA CuYao , Julia CUDAnative. Yao SymEngine, .

-, Julia, Yao . Yao ( CUDA- CuYao) — -, . .

, , . , , .

, , Yao .

?

, .
(, OpenQASM), (YaoIR), , ( ) !

- , , . , , !

Julia.

] dev https://github.com/QuantumBFS/QuAlgorithmZoo.jl.git

using Pkg
pkgs = ["Plots", "Flux", "Yao", "YaoExtensions", "StatsBase", "BitBasis", "FFTW", "SymEngine"]

for p in pkgs
    Pkg.add(p)
end

using Yao, YaoExtensions, Plots, StatsBase

--

GHZ — , ( ). , :

—
: 2 — ( )
— , , Q#

— . - , , , , . : , , — , .
. , . — . , , , , . , , , , , , - .
. . . — ( ).
Quirk —

: , , . , IBM , , , .

, , , ! , - :

| G H Z ⟩ = \frac{1}{\sqrt{d}} \sum_{i = 0}^{d - 1} | i ⟩ \otimes \dots \otimes | i ⟩ = \frac{1}{\sqrt{d}} (| 0 ⟩ \otimes \dots \otimes | 0 ⟩ + \dots + | d - 1 ⟩ \otimes \dots \otimes | d - 1 ⟩)

$|\mathrm {GHZ} \rangle ={\frac {1}{\sqrt {d}}}\sum _{i=0}^{d-1}|i\rangle \otimes \cdots \otimes |i\rangle ={\frac {1}{\sqrt {d}}}(|0\rangle \otimes \cdots \otimes |0\rangle +\cdots +|d-1\rangle \otimes \cdots \otimes |d-1\rangle )$

Yao:

circuit = chain(
    4,
    put(1=>X),
    repeat(H, 2:4),
    control(2, 1=>X),
    control(4, 3=>X),
    control(3, 1=>X),
    control(4, 3=>X),
    repeat(H, 1:4),
)

nqubits: 4
chain
├─ put on (1)
│  └─ X gate
├─ repeat on (2, 3, 4)
│  └─ H gate
├─ control(2)
│  └─ (1,) X gate
├─ control(4)
│  └─ (3,) X gate
├─ control(3)
│  └─ (1,) X gate
├─ control(4)
│  └─ (3,) X gate
└─ repeat on (1, 2, 3, 4)
   └─ H gate

, : X, not-gate ( ), , cnot-.
(, )

results = ArrayReg(bit"0101") |> circuit |> r->measure(r, nshots=1000)

hist = fit(Histogram, Int.(results), 0:16)
bar(hist.edges[1] .- 0.5, hist.weights, legend=:none)

, - $\mid 0100 \rangle$ $\mid 1011 \rangle$ .

— :

N = 2^{n} Q F T ∣ x ⟩ = \frac{∥ x ∥}{2^{n / 2}} \sum_{y = 0}^{2^{n} - 1} \exp (2 π i \frac{x y}{N}) ∣ y ⟩

$N = 2^n \\ QFT\mid x \rangle = \frac{\parallel x \parallel }{2^{n/2}}\sum_{y=0}^{2^n-1} \exp\left( 2\pi i \frac{xy}{N} \right) \mid y \rangle$

R_{k} = (\begin{matrix} 1 & 0 \\ 0 & e^{2 π i} / 2^{k} \end{matrix})

$R_k = \begin{pmatrix} 1 & 0\\ 0 & e^{2\pi i}/2^k \end{pmatrix}$

, .

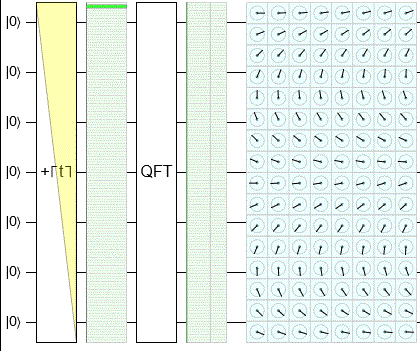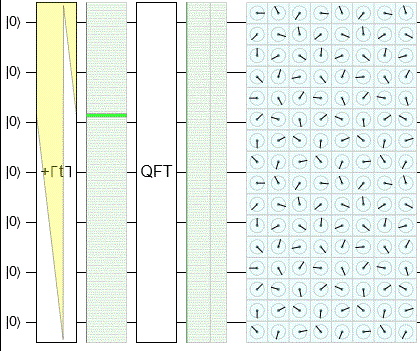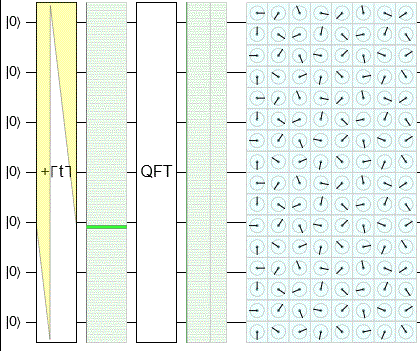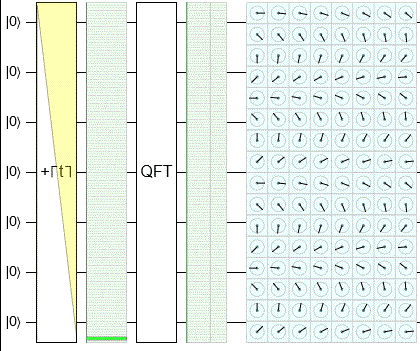
(QFT) , :

B (A ):

A(i, j) = control(i, j=>shift(2π/(1<<(i-j+1))))
R4 = A(4, 1)

# (n -> control(n, 4, 1 => shift(0.39269908169872414)))

, , mat. A $R_4$ :

R4(5)

#nqubits: 5
#control(4)
#└─ (1,) shift(0.39269908169872414)

mat(R4(5))

32×32 LinearAlgebra.Diagonal{Complex{Float64},Array{Complex{Float64},1}}:
 1.0+0.0im      ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅      1.0+0.0im      ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅      1.0+0.0im      ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅      1.0+0.0im         ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
    ⋮                                        ⋱     ⋮                         
     ⋅          ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅      …  1.0+0.0im          ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅      0.92388+0.382683im

i- , i- B. , n, k- .

, B

B(n, k) = chain(n, j==k ? put(k=>H) : A(j, k) for j in k:n)

qft(n) = chain(B(n, k) for k in 1:n)
qft(4)

nqubits: 4
chain
├─ chain
│  ├─ put on (1)
│  │  └─ H
│  ├─ control(2)
│  │  └─ (1,) shift(1.5707963267948966)
│  ├─ control(3)
│  │  └─ (1,) shift(0.7853981633974483)
│  └─ control(4)
│     └─ (1,) shift(0.39269908169872414)
├─ chain
│  ├─ put on (2)
│  │  └─ H
│  ├─ control(3)
│  │  └─ (2,) shift(1.5707963267948966)
│  └─ control(4)
│     └─ (2,) shift(0.7853981633974483)
├─ chain
│  ├─ put on (3)
│  │  └─ H
│  └─ control(4)
│     └─ (3,) shift(1.5707963267948966)
└─ chain
   └─ put on (4)
      └─ H

, A B , , , , .

-, PrimitiveBlock, QFT. , CompositeBlock.

struct QFT{N} <: PrimitiveBlock{N} end
QFT(n::Int) = QFT{n}()
#  
circuit2(::QFT{N}) where N = qft(N)
#     
YaoBlocks.mat(::Type{T}, x::QFT) where T = mat(T, circuit2(x))
YaoBlocks.print_block(io::IO, x::QFT{N}) where N = print(io, "QFT($N)")

using FFTW, LinearAlgebra

function YaoBlocks.apply!(r::ArrayReg, x::QFT)
    α = sqrt(length(statevec(r)))
    invorder!(r)
    lmul!(α, ifft!(statevec(r)))
    return r
end

print_block , QFT . , ,

r = rand_state(5)
r1 = r |> copy |> QFT(5)
r2 = r |> copy |> circuit2(QFT(5))
r1 ≈ r2

# true

, , .

. , , ( ). L . , ver Val(:quantum) Val(:classical), .

using Yao, BitBasis
using YaoExtensions: KMod, QFTCircuit
using QuAlgorithmZoo: NumberTheory

function shor(L::Int, ver=Val(:quantum); maxtry=100)
    L%2 == 0 && return 2

    # find short cut solutions like `a^b`
    res = NumberTheory.factor_a_power_b(L)
    res !== nothing && return res[1]

    for i in 1:maxtry
        # step 1
        x = NumberTheory.rand_primeto(L)

        # step 2
        r = get_order(ver, x, L; )
        if r%2 == 0 && powermod(x, r÷2, L) != L-1
            # step 3
            f1, f2 = gcd(powermod(x, r÷2, L)-1, L), gcd(powermod(x, r÷2, L)+1, L)
            if f1!=1
                return f1
            elseif f2!=1
                return f2
            else
                error("Algorithm Fail!")
            end
        end
    end
end

, :

, L, . . gcd(x, L) == 1. .
x, . . r, mod(x^r, L) == 1. r , x^(r÷2) , , . , L-1 (mod L).
5.2 ,
- gcd(x^(r÷2)-1, L) gcd (x^(r÷2)+1, L) (!=1) L. , powermod(x, r÷2, L) -1, 1, r/2 .

— . NumberTheory, .

,
s / r. , , .

- nshot, nbit ( ) ncbit ( ). nbit , ncbit

"""    ."""
estimate_ncbit(nbit::Int, ϵ::Real) = 2*nbit + 1 + ceil(Int,log2(2+1/2ϵ))

get_order(::Val{:classical}, x::Int, L::Int; kwargs...) = NumberTheory.find_order(x, L)
function get_order(::Val{:quantum}, x::Int, L::Int; nshots::Int=10,
            nbit::Int=bit_length(L-1), ncbit::Int=estimate_ncbit(nbit, 0.25))
    c = order_finding_circuit(x, L; nbit=nbit, ncbit=ncbit)
    reg = join(product_state(nbit, 1), zero_state(ncbit))

    res = measure(copy(reg) |> c; nshots=nshots)
    for r in res
        # split bit string b into lower bits `k` and higher bits `r`.
        mask = bmask(1:ncbit)
        k,i = r&mask, r>>ncbit
        # get s/r
        ϕ = bfloat(k)  #
        ϕ == 0 && continue

        # order_from_float: given a floating point number,
        # return the closest rational number with bounded number of continued fraction steps.
        order = NumberTheory.order_from_float(ϕ, x, L)
        if order === nothing
            continue
        else
            return order
        end
    end
    return nothing
end

order_finding_circuit(x::Int, L::Int; nbit::Int=bit_length(L-1), ncbit::Int=estimate_ncbit(nbit, 0.25)) -> AbstractBlock

x L,
|1>⊗|0> "" .

function order_finding_circuit(x::Int, L::Int; nbit::Int, ncbit::Int)
    N = nbit+ncbit
    chain(N, repeat(N, H, 1:ncbit), KMod{N, ncbit}(x, L),
        subroutine(N, qft_circuit(ncbit)', 1:ncbit))
end

KMod mod(a^k*x, L).
k — , k ( ncbit) , N-K a. , , , Yao. , , .
.

, - - :

@time shor(35, Val(:quantum))

# 2.287219 seconds (14.37 k allocations: 113.341 MiB, 1.38% gc time)
# 5

@time shor(35, Val(:classical))
# 0.000208 seconds (6 allocations: 224 bytes)
# 5

, . : , , .. , , .

, , .

Julia y la computación cuántica

?

--

More articles: