Buen día.
En mi tiempo libre hice un poco de investigación.
En la teoría de gráficos, se conoce un algoritmo codicioso de número de clics. Lejos de siempre, da el resultado correcto. Debajo del corte hay un análisis de los resultados del algoritmo codicioso cuando se combina con la enumeración parcial de los conjuntos de vértices en los gráficos del conjunto de referencia DIMACS.
La columna "Mejor conocida" de la tabla 1 muestra los tamaños de los clics máximos actualmente conocidos de los gráficos indicados. La columna "Codicioso" muestra los tamaños máximos de clics encontrados por el algoritmo codicioso. El algoritmo codicioso da la respuesta correcta solo en 3 casos de 35.
Nota: en el código del programa implementado, el algoritmo codicioso selecciona el vértice con el valor de adyacencia más alto. Si se encuentran varios vértices similares, se selecciona el primero encontrado. Llamaremos al procedimiento de algoritmo codicioso Greedy (A), donde A es el número de la matriz (matriz de adyacencia) a la que se aplica el algoritmo. Indice la matriz inicial como A0.
Tabla 1 - Los resultados del algoritmo implementado en Pascal.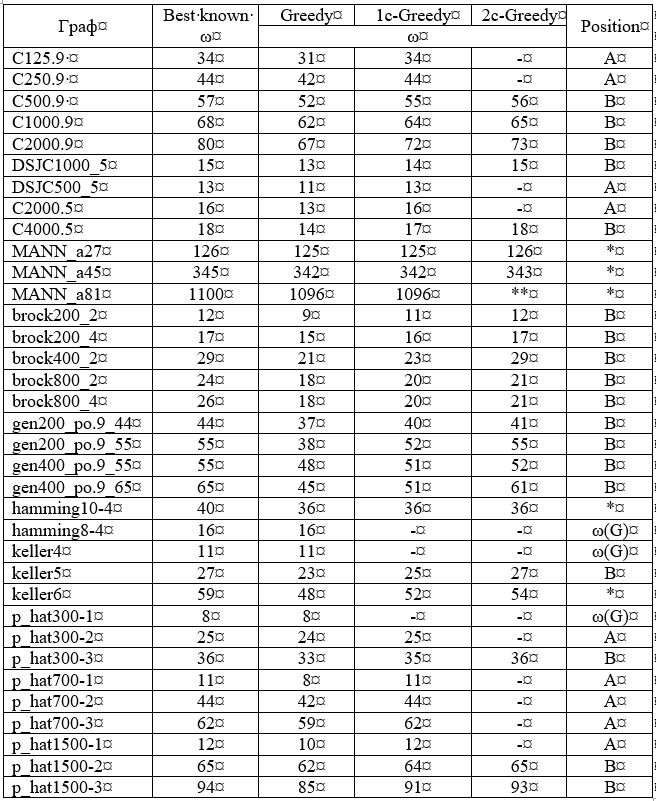 ** - no analizado debido al gran tamaño del gráfico.
** - no analizado debido al gran tamaño del gráfico., : N , . m, m – . DelNotAdj(m).
Greedy(m). ( ) «1c-Greedy». , , 8 35.
. , DelNotAdj(m). 0, m. mx. Greedy(mx). ( ) «2-Greedy».
3- (3c-Greedy) C500.9 C1000.9 ω(C500.9)=57, ω(C1000.9)=66.
.
Pascal Greedy(A) O(n2), n – . n , 2- – .. , ω(G) – () . .
, , ? 1 , .
( 1). O(n), – ω 1 ω(G) – , ωGR – , .
 1
1«Position» 1 . ꞷ(G) , . «» , .
«B» , 2- .
«*» , «», .. 2, 3 . ω. ωGRCFG.
, , , , . .. , , , 2- .
«» , :
- 0 «» . ωGR.
- «» m, m . m , . ωGR+1.
- «» mn, m- n- 0. mn , n- m- . ωGR+2.
- 3-, 4-,…, y- ωGR+3, ωGR+4,…, ωGR+y .
- 0 — ω(G).
. «» «B» :
, , ωGR. ωGR+1 ωGR, 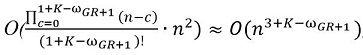 , K – .
, K – .
«*» :
«» ωGR, ωGR+1, ωGR+2,…, ω(G) . , , . , ωGR.
: ωGR, ωGR+1, ωGR+2,… , « » ( ωGRCDE 1).
:
1. «» ωGR+y,
ωGR+y-1, 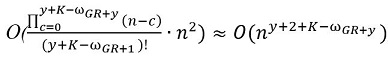 , K – .
, K – .
.
2. y- ωGR+y, , .. ωGR+y=ωGR+y-1, , ωGR+y ω(G) .
Si lo anterior repite el trabajo de otra persona, no estoy por despecho, me alegrará ver el enlace. Me alegraría aún más si alguien teóricamente puede probar o refutar las hipótesis propuestas.