Matemáticas borrosas. Relaciones y colas de lobo

Los parámetros y principios de funcionamiento de varios sistemas se pueden conectar mediante un atributo seleccionado entre ellos con varios tipos de relaciones. Si, digamos, estamos interesados ​​en el efecto del precio de un servicio en su demanda, entonces esta relación puede describirse por una relación del tipo "influencias", "influencias fuertes", "influencias débiles", etc. En este caso, los objetos bastante "discretos" para la descripción pueden no ser suficientes. Para muchos problemas aplicados de la teoría de autómatas, reconocimiento de patrones, toma de decisiones, etc. Tiene sentido generalizar el concepto de la relación entre los objetos a un caso difuso. Además, el modelo, muy posiblemente, describirá de manera más adecuada el sistema, permitiendo un análisis cualitativo de los sistemas sin pérdida de información umbral, en relación con la aparición de nuevos tipos de relaciones: similitud, similitud, disimilitud, ...

El concepto de relaciones difusas (conexiones, asociaciones, relaciones, relaciones son sinónimos), junto con el concepto de conjuntos difusos, se refiere a los fundamentos fundamentales de toda la teoría de los conjuntos difusos. Además del hecho de que ellos mismos han aplicado valor, sobre la base de una serie de conceptos adicionales se determinan que se utilizan para construir modelos difusos de sistemas más complejos.

Relación borrosa

(lo siento)

Definición

Como en el caso de los conjuntos difusos (HM), las relaciones difusas generalizan el concepto de la relación habitual a la que estamos acostumbrados en la teoría de conjuntos (ingenua). Y muchos conceptos presentados a continuación para las relaciones serán similares a los conceptos correspondientes para NM.

Introducimos los conceptos de relación difusa y consideramos sus propiedades.

Relación difusa de 2 arios (binario) $$$R$$$$U = U_1 \times U_2$$$$U_1 \times U_2$, $$$\mu_R(x, y) : U_1 \times U_2 \mapsto [0, 1], x \in U_1, y \in U_2$. :

$$

$$R = \bigcup_{(x, y) \in U_1 \times U_2} \mu_R(x, y) / (x, y)$$

n- $$$R$n- .

, $$$[0, 1]$- ( , ..). $$$[0, 1]$. $$$\mu_R(x, y)$$$$(x, y)$$$$xRy \Leftrightarrow (x, y) \in R$. , n- .

.

• ;
• $$$(x_i, y_j)$$$$\mu_R(x_i, y_j)$;
• $$$||\mu_R(x_i, y_j)||$;
• $$$\widetilde{G} = (\widetilde{U}, \widetilde{V})$, $$$\widetilde{U} = \left\{ u_n \right\}, n \in \mathbb{N}$— , $$$\widetilde{V} = \left\{ \rangle \mu_{\widetilde{R}}(u_i, u_j) / (u_i, u_j) \langle, \mu_{\widetilde{R}}(u_i, u_j) > 0 \right\}$— . ( , . , , , xD)

.

$$$R, S$— $$$U_1 \times U_2, x \in U_1, y \in U_2$

$$$R$$$$U$$$$U_1 \times U_2$:

$$

$$supp(R) = \left\{ (x, y): \mu_R(x, y) > 0, (x, y) \in U_1 \times U_2 \right\}$$

$$$R$$$$S$,

$$

$$\forall (x, y) \Rightarrow \mu_R(x, y) \leq \mu_S(x, y)$$

( ) :

$$

$$\mu_R^{(1)}(x, y) = max_y(\mu_R(x, y))$$

:

$$

$$\mu_R^{(2)}(x, y) = max_x(\mu_R(x, y))$$

$$$h(R)$:

$$

$$h(R) = max_x(max_y(\mu_R(x, y))) = max_y(max_x(\mu_R(x, y)))$$

, $$$h(R) = 1$, — .

$$$R$$$$\bar{R}$, :

$$

$$\mu_{\bar{R}}(x, y) = 1 - \mu_R(x, y)$$

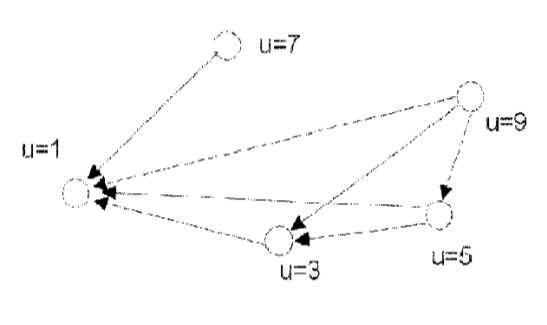
, $$$R$llamar a una relación tan clara $$$R_{} | \mu_{R_}(x, y) = \begin{cases}0, & \mu_R(x, y) < 0.5 \\ 1, & \mu_R(x, y) > 0.5 \\ 0 1, & \mu_R(x, y) = 0.5 \end{cases}.$En general, se acepta que cuando la función característica de la relación difusa es 0.5, la función para el cierre será 0.

Inversa a $$$R$llamar a tal actitud $$$R^{-1}$, qué $$$\mu_{R^{-1}}(x, y) = \mu_R(y, x).$Matriz de relaciones $$$R^{-1}$en este caso será la matriz transpuesta $$$R$.

Operaciones

Unión e intersección :

$$

$$\mu_{R \cup S}(x, y) = max(\mu_R(x, y), \mu_S(x, y));\\ \mu_{R \cap S}(x, y) = min(\mu_R(x, y), \mu_S(x, y))$$

. El conjunto de todas las relaciones difusas forma una red distributiva en relación con las operaciones de unión e intersección; y del cumplimiento de las identidades de idempotencia, conmutatividad, asociatividad, absorción y distributividad para la red.$$$L = [0; 1]$ El cumplimiento de estas identidades para todas las relaciones sigue.

, , « x y / » « x y ». ; , «» , x y , . , .

: $$$\mu_{R \cdot S}(x, y) = \mu_R(x, y) \cdot \mu_S(x, y)$; : $$$\mu_{R + S}(x, y) = \mu_R(x, y) + \mu_S(x, y) - \mu_R(x, y) \cdot \mu_S(x, y)$.

, . $$$\alpha$- . , . - $$$R_{\alpha} = \left\{ (x, y): \mu_R(x, y) \geq \alpha \right\}$. , $$$\alpha_1 \geq \alpha_2 \Rightarrow R_{\alpha_1} \subset R_{\alpha_2}$.

( ) . $$$R$$$$R = max_{\alpha}(\alpha \times R_{\alpha})$.

. , . (Max-*)-. , 3 .

1. max-min ( ): $$$RS : \mu_{RS}(x, z) = max_{y \in U}(min(\mu_R(x, y), \mu_S(y, z)))$. .
2. min-max ( ): $$$R \circ S : \mu_{R \circ S}(x, z) = min_{y \in U}(max(\mu_R(x, y), \mu_S(y, z)))$.
3. max-• ( ): $$$R * S : sup_{y \in U}(\mu_R(x, y) \cdot \mu_S(y, z))$.

. :

:$$$\mu_R(x, x) = 1, \forall (x, x) \in U$;

: $$$\mu_R(x, y) \leq \mu_R(x, x)$;

: $$$\mu_R(x, x) = 1, \mu_R(x, y) < 1$;

flexx: $$$\mu_R(x, x) = 0, \forall (x, x) \in U$;

: $$$\mu_R(x, y) = \mu_R(y, x)$;

: $$$\mu_R(x, y) \neq \mu_R(y, x) \vee_{()} \mu_R(x, y) = \mu_R(y, x) = 0$;

: $$$x \neq y, \mu_R(x, y) > 0 \Rightarrow \mu_R(y, x) = 0$;

: $$$\mu_R(x, z) \geq max_y(min(\mu_R(x, y), \mu_R(y, z)))$.

… . .

2 NPC-, $$$K_1$$$$K_2$. , . NPC :

$$$K_1:$, , .

$$$K_2:$, , — .

, , :

« » $$$= A = (0.8/3; 0.4/15; 0.3/30).$

« » $$$= B = (0.1/0.9; 0.5/0.5; 0.8/0.1).$

« » $$$= C = (0.8/0.9; 0.5/0.5; 0.3/0.2).$

. : NPC ?

, :

def very(arr: List[set]):
    return [(elem[0]**2, elem[1]) for elem in arr]


def no(arr: List[set]):
    return [(1 - elem[0], elem[1]) for elem in arr]


def attitude(a: List[set], b: List[set], func = lambda x, y: min(x, y)):
    return [[func(i[0], j[0]) for j in b] for i in a]


def attitude_unite(a: List[List], b: List[List]):
    return [[max(a[i][j], b[i][j]) for j in range(len(a[i]))] for i in range(len(a))]


def composition(a: List[List], b: List[List]):
    result = [[0 for j in range(len(b[0]))] for i in range(len(a))]

    for x in range(len(a)):
        for z in range(len(b[0])):
            maximum = min(a[x][0], b[0][z])

            for y in range(0, len(a[0])):
                if maximum < min(a[x][y], b[y][z]):
                    maximum = min(a[x][y], b[y][z])
            
            result[x][z] = maximum

    return result


def index_plus(a: List[List]):
    maximum = max([elem[1] for elem in a])
    result = 0
    for i in range(len(a)):
        result += a[i][0] * (a[i][1] + maximum) / 2

    return result


def ranking_index(a: List[List], b: List[List]):
    return index_plus(a) - index_plus(b)

, — -. , , , index_plus ranking_index. . ( ; , ) :

$$

$$H(A, B) = H_+(A) - H_+(B), \\ \ H_+(X) = \int_{0}^{1}M(X_0)dX, \\ M(X_0) = \frac{(inf_{x \in X_0}(x) + sup_{x \in X_0}(x)) }{2}.$$

$$$A$$$$B$— . . :

A = [(0.8, 3), (0.4, 15), (0.3, 30)]
B = [(0.1, 0.9), (0.5, 0.5), (0.8, 0.1)]
C = [(0.8, 0.9), (0.5, 0.5), (0.3, 0.2)]

$$$x$— « ». $$$" \ \ " = \overline{" \ "} = \overline{CON("")}.$1 3 :

x = no(very(A))
x = [[elem[0] for elem in x]]

NPC $$$K_1$R1. $$$R_1 = A \times B \ \cup \ \overline{A} \times \overline{B}$:

AonB = attitude(A, B)
notAonnotB = attitude(no(A), no(B))
R1 = attitude_unite(AonB, notAonnotB)

$$$y_1$, ( ) $$$R_1$.

y1 = composition(x, R1)
print('y1 = ', y1)
# >> y1 =  [[0.63, 0.3599999999999999, 0.3599999999999999]]

:

notAonC = attitude(no(A), C)
AonnotC = attitude(A, no(C))
R2 = attitude_unite(notAonC, AonnotC)
y2 = composition(x, R2)
print('y2 = ', y2)
# >> y2 =  [[0.5599999999999999, 0.3599999999999999, 0.3599999999999999]]

$$$y_1$$$$y_2$:

y1 = [(y1[0][i], B[i][1]) for i in range(len(y1[0]))]
y2 = [(y2[0][i], C[i][1]) for i in range(len(y2[0]))]

NPC:

print('index = ', ranking_index(y1, y2))
# >> index =  -0.020000000000000018

Un pequeño valor negativo indica que $$$K_2$acepta más objetos con lealtad y es más probable que cuente la búsqueda del jugador que $$$K_1$.

Y eso es todo por hoy.