Hola Habr!Le recordamos que anteriormente anunciamos el libro " Aprendizaje automático sin palabras adicionales ", y ahora ya está a la venta . A pesar del hecho de que para los principiantes en MO, el libro puede convertirse en un escritorio , algunos temas aún no se tocaron. Por lo tanto, estamos ofreciendo a todos los interesados una traducción de un artículo de Simon Kerstens sobre la esencia de los algoritmos MCMC con la implementación de dicho algoritmo en Python.Los métodos de Monte Carlo para las cadenas de Markov (MCMC) son una clase poderosa de métodos para el muestreo a partir de distribuciones de probabilidad que se conocen solo hasta una cierta constante (desconocida) de normalización.Sin embargo, antes de profundizar en el MCMC, analicemos por qué incluso podría necesitar hacer tal selección. La respuesta es: puede interesarle las muestras de la muestra (por ejemplo, para determinar parámetros desconocidos utilizando el método de derivación bayesiano) o para aproximar los valores esperados de las funciones en relación con la distribución de probabilidad (por ejemplo, calcular cantidades termodinámicas a partir de la distribución de estados en física estadística). A veces solo nos interesa el modo de distribución de probabilidad. En este caso, lo obtenemos por el método de optimización numérica, por lo que no es necesario hacer una selección completa.Resulta que el muestreo de cualquier distribución de probabilidad, excepto las más primitivas, es una tarea difícil. El método de transformación inversa es una técnica elemental para el muestreo de distribuciones de probabilidad, que, sin embargo, requiere el uso de una función de distribución acumulativa, y para usarla, a su vez, debe conocer la constante de normalización, que generalmente es desconocida. En principio, se puede obtener una constante de normalización por integración numérica, pero este método rápidamente se vuelve impracticable con un aumento en el número de dimensiones. Muestreo de desviacionesNo requiere una distribución normalizada, pero para implementarla de manera efectiva, se necesita saber mucho sobre la distribución que nos interesa. Además, este método sufre severamente por la maldición de las dimensiones, esto significa que su efectividad disminuye rápidamente con un aumento en el número de variables. Es por eso que necesita organizar de manera inteligente la recepción de muestras representativas de su distribución, sin necesidad de conocer la constante de normalización.Los algoritmos MCMC son una clase de métodos diseñados específicamente para esto. Vuelven al artículo histórico de Metrópolis y otros ; Metropolis desarrolló el primer algoritmo MCMC que lleva su nombrey diseñado para calcular el estado de equilibrio de un sistema bidimensional de esferas duras. De hecho, los investigadores estaban buscando un método universal que nos permitiera calcular los valores esperados encontrados en la física estadística.Este artículo cubrirá los conceptos básicos del muestreo MCMC.CADENAS MARKOVAhora que entendemos por qué necesitamos muestrear, pasemos al corazón de MCMC: las cadenas de Markov. ¿Qué es una cadena de Markov? Sin entrar en detalles técnicos, podemos decir que una cadena de Markov es una secuencia aleatoria de estados en un determinado espacio de estados, donde la probabilidad de elegir un determinado estado depende solo del estado actual de la cadena, pero no de su historia pasada: esta cadena carece de memoria. Bajo ciertas condiciones, una cadena de Markov tiene una distribución estacionaria única de estados, a la que converge, superando un cierto número de estados. Después de tal cantidad de estados en una cadena de Markov, se obtiene una distribución invariable.Para tomar muestras de una distribución, 
el algoritmo MCMC crea y simula una cadena de Markov cuya distribución estacionaria es; esto significa que después del período inicial de "semilla", los estados de dicha cadena de Markov se distribuyen de acuerdo con el principio . Por lo tanto, solo tendremos que guardar el estado para obtener muestras .Para fines educativos, consideremos un espacio de estado discreto y un "tiempo" discreto. La cantidad clave que caracteriza una cadena de Markov es un operador de transición que 
indica la probabilidad de estar en un estado 
a la vez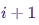 
, siempre que la cadena esté en un estado 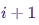a la vez i.Ahora solo por diversión (y como demostración) tejemos rápidamente una cadena de Markov con una distribución estacionaria única. Comencemos con algunas importaciones y configuraciones para gráficos:%matplotlib notebook
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 6]
np.random.seed(42)
La cadena de Markov girará alrededor del espacio de estado discreto formado por tres condiciones climáticas:state_space = ("sunny", "cloudy", "rainy")
En un espacio de estado discreto, el operador de transición es solo una matriz. En nuestro caso, las columnas y filas corresponden al clima soleado, nublado y lluvioso. Elijamos valores relativamente razonables para las probabilidades de todas las transiciones:transition_matrix = np.array(((0.6, 0.3, 0.1),
(0.3, 0.4, 0.3),
(0.2, 0.3, 0.5)))
Las filas indican los estados en los que el circuito puede estar ubicado actualmente, y las columnas indican los estados en los que puede ir el circuito. Si damos el paso de "tiempo" de la cadena de Markov en una hora, entonces, siempre que esté soleado ahora, hay un 60% de posibilidades de que el clima soleado continúe durante la próxima hora. También hay un 30% de posibilidades de que haya un clima nublado en la próxima hora, y un 10% de posibilidades de que llueva inmediatamente después de un clima soleado. También significa que los valores en cada fila suman uno.Conduzcamos un poco nuestra cadena de Markov:n_steps = 20000
states = [0]
for i in range(n_steps):
states.append(np.random.choice((0, 1, 2), p=transition_matrix[states[-1]]))
states = np.array(states)
Podemos observar cómo la cadena de Markov converge a una distribución estacionaria, calculando la probabilidad empírica de cada uno de los estados en función de la longitud de la cadena:def despine(ax, spines=('top', 'left', 'right')):
for spine in spines:
ax.spines[spine].set_visible(False)
fig, ax = plt.subplots()
width = 1000
offsets = range(1, n_steps, 5)
for i, label in enumerate(state_space):
ax.plot(offsets, [np.sum(states[:offset] == i) / offset
for offset in offsets], label=label)
ax.set_xlabel("number of steps")
ax.set_ylabel("likelihood")
ax.legend(frameon=False)
despine(ax, ('top', 'right'))
plt.show()
HONOR DE TODAS LAS MCMC: ALGORITMO DE METROPOLIS-HASTINGSPor supuesto, todo esto es muy interesante, pero volviendo al proceso de muestreo de una distribución de probabilidad arbitraria 
. Puede ser discreto, en cuyo caso continuaremos hablando sobre la matriz de transición 
, o continuo, en cuyo caso será un núcleo de transición. En lo sucesivo, hablaremos sobre distribuciones continuas, pero todos los conceptos que consideramos aquí también son aplicables a casos discretos.Si pudiéramos diseñar el núcleo de transición de tal manera que ya se dedujera el siguiente estado , entonces esto podría ser limitado, ya que nuestra cadena de Markov ... tomaría muestras directamente . Desafortunadamente, para lograr esto, necesitamos la capacidad de tomar muestras delo que no podemos hacer; de lo contrario, no leerías eso, ¿verdad?La solución consiste en dividir el núcleo de transición 
en dos partes: el paso de propuesta y el paso de aceptación / rechazo. Aparece una distribución auxiliar en el paso de muestra
de donde se seleccionan los posibles estados siguientes de la cadena. No solo podemos hacer una selección de esta distribución, sino que también podemos elegir arbitrariamente la distribución en sí. Sin embargo, al diseñar, uno debe esforzarse por llegar a una configuración en la que las muestras tomadas de esta distribución se correlacionen mínimamente con el estado actual y al mismo tiempo tengan buenas posibilidades de pasar por la fase de recepción. El paso anterior de recepción / descarte es la segunda parte del núcleo de transición; en esta etapa, los errores contenidos en los estados de prueba seleccionados se corrigen 
. Aquí, se calcula la probabilidad de una recepción exitosa 
y se toma una muestra con una probabilidad tal como el siguiente estado en la cadena. Obteniendo el siguiente estado deluego se realiza de la siguiente manera: primero, se toma el estado de prueba . Luego se toma como el siguiente estado con probabilidad o se descarta con probabilidad 
, y en el último caso, el estado actual se copia y se usa como el siguiente.En consecuencia, hemos
condición suficiente para la cadena de Markov tenía como una distribución estacionaria es la siguiente: El núcleo de transición debe presentar equilibrio detallado o como escritura en la literatura física, la reversibilidad microscópica :
.Esto significa que la probabilidad de estar en un estado 
y moverse de allí a
debe ser igual a la probabilidad del proceso inverso, es decir, poder y entrar en un estado . Los núcleos de transición de la mayoría de los algoritmos MCMC satisfacen esta condición.Para que el núcleo de transición de dos partes obedezca al equilibrio detallado, es necesario elegir correctamente 
, es decir, para asegurarse de que le permite corregir cualquier asimetría en el flujo de probabilidad de / ao . Metropolis-Hastings algoritmo utiliza criterio de admisibilidad metrópolis:
.Y aquí comienza la magia: solo conocemos una constante, pero no importa, ya que esta constante desconocida anula la expresión para! Es esta propiedad paccpacc la que garantiza el funcionamiento de algoritmos basados en el algoritmo de Metropolis-Hastings en distribuciones no normalizadas. Con frecuencia se utilizan distribuciones auxiliares simétricas c 
, en cuyo caso el algoritmo Metropolis-Hastings se reduce al algoritmo Metropolis original (menos general) desarrollado en 1953. En el algoritmo original
.En este caso, el núcleo de transición completo de Metropolis-Hastings se puede escribir como
.IMPLEMENTAMOS EL ALGORITMO METROPOLIS-HASTINGS EN PYTHONBueno, ahora que hemos descubierto cómo funciona el algoritmo Metropolis-Hastings, pasemos a su implementación. Primero, establecemos la probabilidad logarítmica de la distribución a partir de la cual vamos a hacer una selección, sin constantes de normalización; se supone que no los conocemos. A continuación, trabajamos con la distribución normal estándar:def log_prob(x):
return -0.5 * np.sum(x ** 2)
A continuación, elegimos una distribución auxiliar simétrica. En general, el rendimiento del algoritmo Metropolis-Hastings se puede mejorar al incluir en la distribución auxiliar la información que ya conoce sobre la distribución de la que desea realizar una selección. Un enfoque simplificado se ve así: tomamos el estado actual xy seleccionamos una muestra de , es decir, establecemos un cierto tamaño de paso Δy vamos a la izquierda o derecha de nuestro estado actual por no más de 
:def proposal(x, stepsize):
return np.random.uniform(low=x - 0.5 * stepsize,
high=x + 0.5 * stepsize,
size=x.shape)
Finalmente, calculamos la probabilidad de que la propuesta sea aceptada:def p_acc_MH(x_new, x_old, log_prob):
return min(1, np.exp(log_prob(x_new) - log_prob(x_old)))
Ahora ponemos todo esto en una implementación verdaderamente breve de la etapa de muestreo para el algoritmo Metropolis-Hastings:def sample_MH(x_old, log_prob, stepsize):
x_new = proposal(x_old, stepsize)
accept = np.random.random() < p_acc(x_new, x_old, log_prob)
if accept:
return accept, x_new
else:
return accept, x_old
Además del siguiente estado en la cadena de Markov, x_newo x_oldtambién devolvemos información sobre si se adoptó el paso MCMC. Esto nos permitirá rastrear la dinámica de la recolección de muestras. En conclusión de esta implementación, escribimos una función que llamará iterativamente sample_MHy, por lo tanto, construirá una cadena de Markov:def build_MH_chain(init, stepsize, n_total, log_prob):
n_accepted = 0
chain = [init]
for _ in range(n_total):
accept, state = sample_MH(chain[-1], log_prob, stepsize)
chain.append(state)
n_accepted += accept
acceptance_rate = n_accepted / float(n_total)
return chain, acceptance_rate
PROBANDO NUESTRO ALGORITMO DE METROPOLIS-HASTINGS E INVESTIGANDO SU COMPORTAMIENTOProbablemente, ahora no puede esperar para ver todo esto en acción. Haremos esto, tomaremos algunas decisiones informadas sobre los argumentos stepsizey n_total:chain, acceptance_rate = build_MH_chain(np.array([2.0]), 3.0, 10000, log_prob)
chain = [state for state, in chain]
print("Acceptance rate: {:.3f}".format(acceptance_rate))
last_states = ", ".join("{:.5f}".format(state)
for state in chain[-10:])
print("Last ten states of chain: " + last_states)
Acceptance rate: 0.722
Last ten states of chain: -0.84962, -0.84962, -0.84962, -0.08692, 0.92728, -0.46215, 0.08655, -0.33841, -0.33841, -0.33841
Las cosas son buenas. Entonces, ¿funcionó? Logramos tomar muestras en aproximadamente el 71% de los casos, y tenemos una cadena de estados. Los primeros estados en los que la cadena aún no ha convergido a su distribución estacionaria deben descartarse. Verifiquemos si las condiciones que hemos elegido tienen una distribución normal:def plot_samples(chain, log_prob, ax, orientation='vertical', normalize=True,
xlims=(-5, 5), legend=True):
from scipy.integrate import quad
ax.hist(chain, bins=50, density=True, label="MCMC samples",
orientation=orientation)
if normalize:
Z, _ = quad(lambda x: np.exp(log_prob(x)), -np.inf, np.inf)
else:
Z = 1.0
xses = np.linspace(xlims[0], xlims[1], 1000)
yses = [np.exp(log_prob(x)) / Z for x in xses]
if orientation == 'horizontal':
(yses, xses) = (xses, yses)
ax.plot(xses, yses, label="true distribution")
if legend:
ax.legend(frameon=False)
fig, ax = plt.subplots()
plot_samples(chain[500:], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
¡Se ve genial!¿Qué pasa con los parámetros stepsizey n_total? Primero discutimos el tamaño del paso: determina qué tan lejos se puede eliminar el estado de prueba del estado actual del circuito. Por lo tanto, este es un parámetro de distribución auxiliar qque controla qué tan grandes serán los pasos aleatorios tomados por la cadena de Markov. Si el tamaño del paso es demasiado grande, los estados de prueba a menudo terminan en la cola de la distribución, donde los valores de probabilidad son bajos. El mecanismo de muestreo de Metropolis-Hastings descarta la mayoría de estos pasos, como resultado de lo cual las tasas de recepción se reducen y la convergencia disminuye significativamente. Ver por ti mismo:def sample_and_display(init_state, stepsize, n_total, n_burnin, log_prob):
chain, acceptance_rate = build_MH_chain(init_state, stepsize, n_total, log_prob)
print("Acceptance rate: {:.3f}".format(acceptance_rate))
fig, ax = plt.subplots()
plot_samples([state for state, in chain[n_burnin:]], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
sample_and_display(np.array([2.0]), 30, 10000, 500, log_prob)
Acceptance rate: 0.116
No muy bien, ¿verdad? Ahora parece que es mejor establecer un tamaño de paso pequeño. Resulta que esta tampoco es una decisión inteligente, ya que la cadena de Markov investigará la distribución de probabilidad muy lentamente y, por lo tanto, tampoco convergerá tan rápido como con un tamaño de paso bien elegido:sample_and_display(np.array([2.0]), 0.1, 10000, 500, log_prob)
Acceptance rate: 0.992
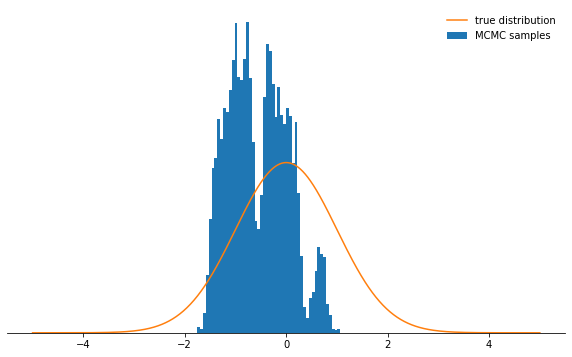Independientemente de cómo elija el parámetro de tamaño de paso, la cadena de Markov finalmente converge a una distribución estacionaria. Pero esto puede llevar mucho tiempo. El tiempo durante el cual simularemos la cadena de Markov está n_totaldeterminado por el parámetro ; simplemente determina cuántos estados de la cadena de Markov (y, por lo tanto, las muestras seleccionadas) finalmente tendremos. Si la cadena converge lentamente, entonces debe incrementarse n_totalpara que la cadena de Markov tenga tiempo de "olvidar" el estado inicial. Por lo tanto, dejaremos el tamaño del paso pequeño y aumentaremos el número de muestras aumentando el parámetro n_total:sample_and_display(np.array([2.0]), 0.1, 500000, 25000, log_prob)
Acceptance rate: 0.990
Estamos avanzando hacia la meta más lentamente ...CONCLUSIONESConsiderando todo lo anterior, espero que ahora haya comprendido intuitivamente la esencia del algoritmo Metropolis-Hastings, sus parámetros, y entienda por qué esta es una herramienta extremadamente útil para seleccionar entre las distribuciones de probabilidad no estándar que puede encontrar en la práctica.Le recomiendo que experimente con el código que se proporciona aquí.- para que te acostumbres al comportamiento del algoritmo en varias circunstancias y lo entiendas más profundamente. ¡Prueba la distribución auxiliar asimétrica! ¿Qué sucederá si no configura el criterio de aceptación correctamente? ¿Qué sucede si intentas tomar muestras de una distribución bimodal? ¿Puedes encontrar una manera de ajustar automáticamente el tamaño del paso? ¿Cuáles son las trampas aquí? ¡Responda estas preguntas usted mismo!