Un deseo excesivo de precisión comenzó a ejercer un efecto que niega la teoría del control y la teoría del sistema, ya que conduce al hecho de que la investigación en esta área se centra en esos y solo aquellos problemas que pueden resolverse con precisión. Muchas clases de problemas importantes en los que los datos, las metas y las restricciones son demasiado complejas o están mal definidas para permitir un análisis matemático preciso se han mantenido y permanecen al margen solo porque no pueden interpretarse matemáticamente. L. Zade
Definición y características
En el mundo, mucho no se divide solo en blanco y negro, en verdad y verdad ... Una persona usa muchos conceptos confusos para evaluar y comparar cantidades físicas, estados de objetos y sistemas en un nivel aproximado y cualitativo. Entonces, cualquiera de nosotros es capaz de estimar la temperatura fuera de la ventana, sin recurrir a un termómetro, y guiados solo por nuestros propios sentimientos y una escala de estimaciones aproximadas ("lo suficientemente nublado como para llevar un paraguas").
Pero una evaluación cualitativa no posee la propiedad de aditividad inherente a nuestros números habituales; es decir, no podemos determinar el resultado de las operaciones para estimaciones aproximadas ("una pequeña cantidad de dinero" + "una pequeña cantidad de dinero"), en contraste con, por ejemplo, los números naturales (2 + 2). No podemos determinar porque una evaluación cualitativa depende en gran medida del tomador de decisiones, el contexto y el significado invertido en un caso particular.
Sin embargo, en el mundo hay cantidades suficientes que no podemos evaluar con precisión por una razón u otra: el grado de orden en la habitación, el "prestigio" del automóvil, la belleza de una persona, la "similitud" de las cosas ... Pero quiero trabajar con ellos como con los números habituales sería para tareas de automatización.
. 1964 .
.
( )  () U
() U )%20) ,
,  ,
,
%20) —
—  ,
, ![\ mu_A (u): U → [0; 1]](https://tex.s2cms.ru/svg/%20%5Cmu_A%20(u)%3AU%20%E2%86%92%5B0%3B1%5D%20) .
. %7D(%5Cmu_A%20(u)%20%2F%20u)%20%3D%20%5Cleft%5C%7B%20%20(%5Cmu_A(u)%20%2F%20u)%20%5Cright%5C%7D%20%20) .
.
U %20) ( ) u (-)
( ) u (-)  . , . - .
. , . - .
%20) ( . ), – . – U
( . ), – . – U  . , , .
. , , .
, %20%3D%20%5Cbegin%7Bcases%7D1%20%26%20u%20%5Csubseteq%20A%20%5C%5C0%20%26%20u%20%5Cnsubseteq%20A%20%5Cend%7Bcases%7D%20) , .
, .
, %20) :
:
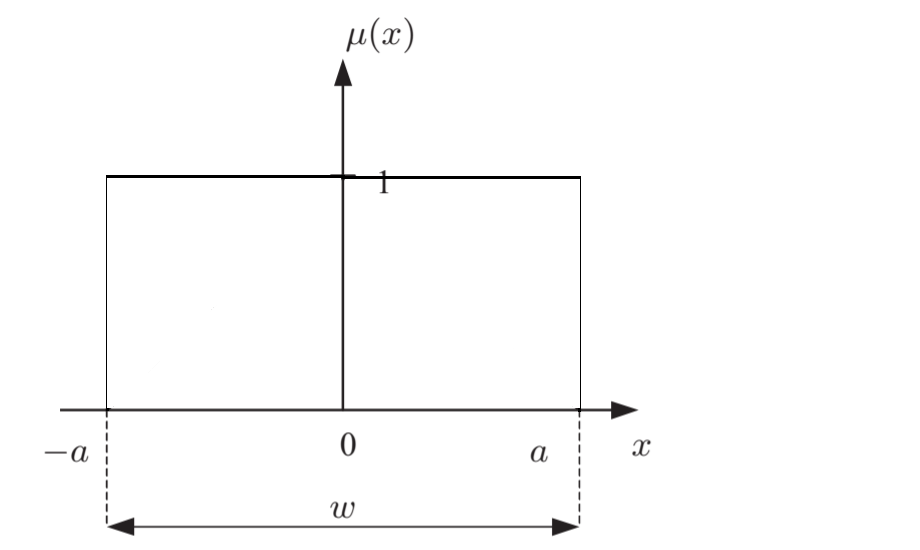
-a≤x≤a.
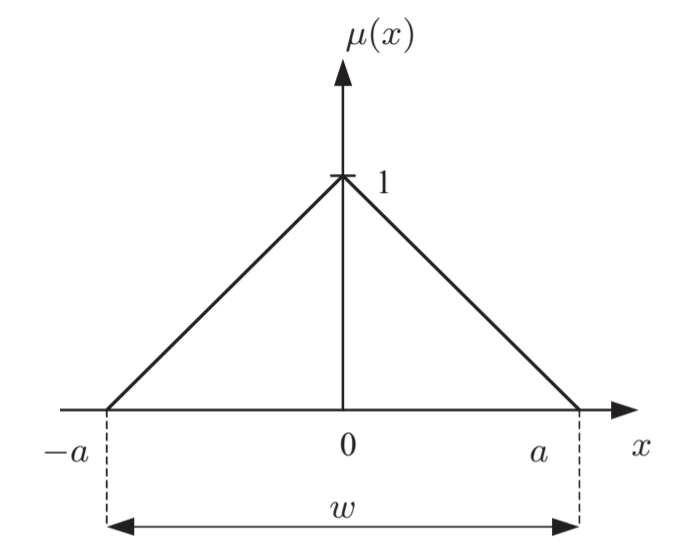
“ ”.
%3D%20%5Cfrac%7B(a-%7Cx%7C)%7D%7Ba%7D%2C%20%20-a%20%5Cleq%20x%20%5Cleq%20a%20)
 .
.
.
– , 1. 0.
, %20) 0.5, . -a/2 a/2.
0.5, . -a/2 a/2.
)%2Cu%20%5Csubseteq%20U%20) .
.
, 1, . – .
, , 0, .
, 1 .
2 %20)
%3E0%2C%20%20x%20%5Csubseteq%20X%20%5Cright%5C%7D%20) –
–  .
. 
 .
.
, x, %3D0%20) ; –
; – %7D%3D0%20) .
.
, , . :
- , ;
- , ;
- , , .
:  — U,
— U,  . , .
. , .
 ,
, %3D%20%5Cmu_B(x)%20) .
.
 ,
, %20%5Cleq%20%0A%20%5Cmu_B%20(x)%20) x.
x.
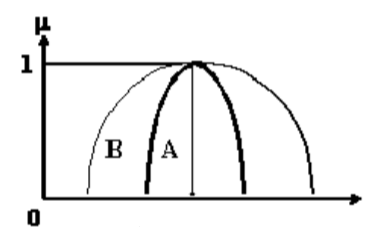
 ,
, %20%3D%20max%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cvee%20%5Cmu_B%20(x)%20) . (t– s–)
. (t– s–)
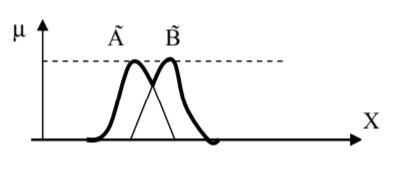
 ,
, %20%3D%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cwedge%20%5Cmu_B%20(x)%20) . (t-)
. (t-)
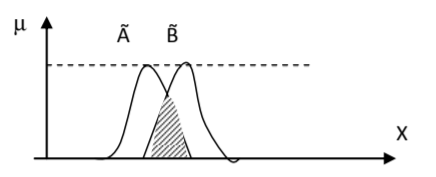
:
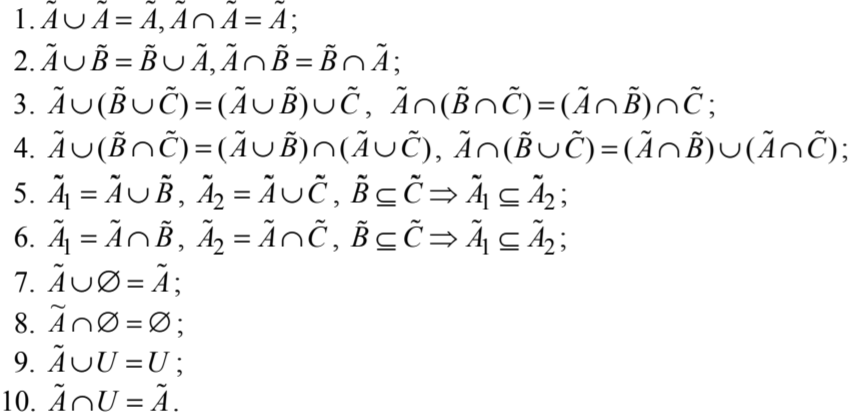
. , , . , min max .
 ,
, %20%3D%20%5Cmu_A(x)%20-%20%5Cmu_%7BA%20%5Ccap%20B%7D(x)%20%3D%20%5Cmu_A(x)%20-%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20%3D%20max(0%3B%20%5Cmu_A(x)%20-%20%5Cmu_B(x))%20) .
.

 . ,
. , %20%3D%201-%20%5Cmu_%7B%5Coverline%7BA%7D%7D(x)%20) .
.
. , , , (,  ). :
). :
α- . α-  ,
, %20%5Cgeq%20%5Calpha%20) .
.
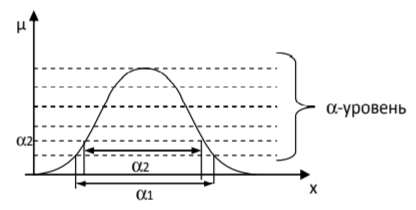
.  , M — .
, M — .
 ,
, %3D%20%5Cmu_A%5E%7B%5Cbeta%7D(x)%20) . :
. :
- β = 2 ( CON(A) ). , . , “ ” ;
- β = 0.5 ( DIL(A) ). , . “ ”.
.
%20%3D%20%5Cmu_A(x)%20*%20%5Cmu_B%20(x)%20) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cvee%200%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%201%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%201%5C%5C0%20%26%20%5Cend%7Bcases%7D%20) .
.
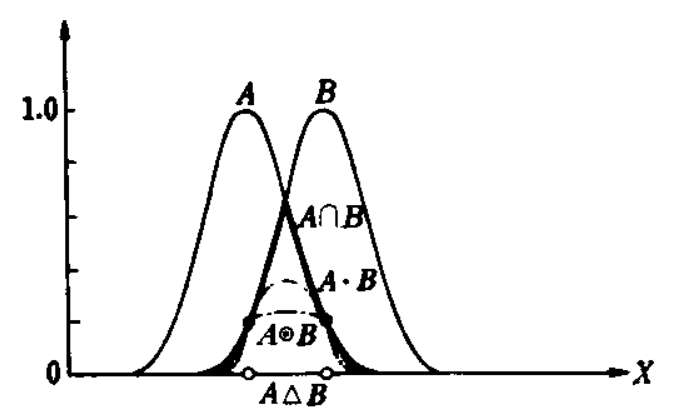
%20%3D%20%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%20%5Cmu_A(x)*%5Cmu_B(x)) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cwedge%201%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%200%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%200%5C%5C1%20%26%20%5Cend%7Bcases%7D%20) .
.
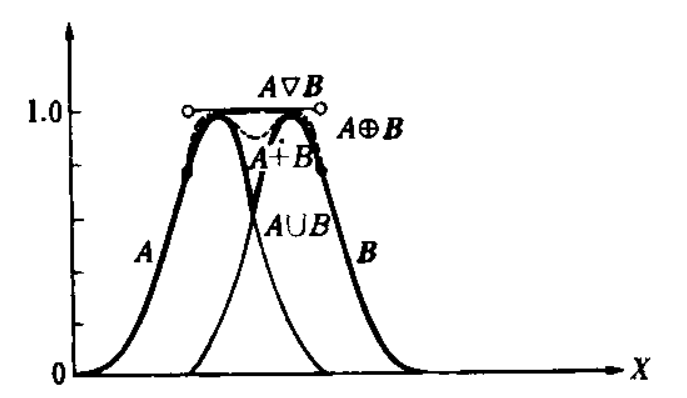
- – A B λ (1 — λ) ( A B). %20%3D%20%5Clambda%20*%20%5Cmu_A(x)%20%2B%20(1%20-%20%5Clambda)%20*%20%5Cmu_B(x)%20) .
.
, λ- :

?
, , . . , ( , ). 2 – .
, . , , , . : , .
, , . , .
, , , , , :
- 0 <= μ(x) <= 1;
- ( );
- La función y el conjunto de funciones definidas deben tener una diferenciación natural de conceptos representados por conjuntos vecinos;
- No debe haber vacíos en el conjunto universal (o limitado para consideración) para el que no se asocia ningún conjunto;
- Para conjuntos adyacentes, el máximo de uno debe coincidir con el mínimo del otro, y el punto de intersección de sus gráficos debe corresponder a los puntos de transición;
- y algunas otras tareas específicas.
aunque hay situaciones excepcionales en las que una función debe determinarse en función del contexto. La construcción de tales funciones es un tema separado y bastante complicado.
Y eso es todo por hoy.