👧🏿 💡 😹 ¿Cómo se implementan los tipos enteros muy largos en Python? 🤥 🖖🏼 🏉

Se preparó una traducción del artículo específicamente para los estudiantes del curso Python Developer .

Cuando escribe en un lenguaje de bajo nivel, como C, le preocupa elegir el tipo de datos y calificadores adecuados para sus enteros, en cada paso analiza si será suficiente para usarlo simplemente into si necesita agregarlo longo incluso agregarlo long double. Sin embargo, al escribir código en Python, no necesita preocuparse por estas cosas "menores", porque Python puede trabajar con números de integercualquier tipo de tamaño.

En C, si intenta calcular 2 ²⁰⁰⁰⁰ utilizando la función incorporada powl, obtendrá la salida inf.

#include <stdio.h>
#include <math.h>

int main(void) {
  printf("%Lf\n", powl(2, 20000));
  return 0;
}

$ ./a.out
inf

Pero en Python, hacer esto más fácil que nunca es fácil:

>>> 2 ** 20000
39802768403379665923543072061912024537047727804924259387134 ...
...
... 6021 digits long ...
...
6309376

¡Debe estar bajo el capó que Python está haciendo algo muy hermoso, y hoy descubriremos qué hace para trabajar con enteros de tamaño arbitrario!

Presentación y definición

Integer en Python, esta es una estructura C definida de la siguiente manera:

struct _longobject {
    PyObject_VAR_HEAD
    digit ob_digit[1];
};

PyObject_VAR_HEADEs una macro, se expande a PyVarObject, que tiene la siguiente estructura:

typedef struct {
    PyObject ob_base;
    Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;

Otros tipos que tienen PyObject_VAR_HEAD:

PyBytesObject
PyTupleObject
PyListObject

Esto significa que un número entero, como una tupla o una lista, tiene una longitud variable, y este es el primer paso para comprender cómo Python puede soportar trabajar con números gigantes. Una vez expandida, la macro _longobjectpuede considerarse como:

struct _longobject {
    PyObject ob_base;
    Py_ssize_t ob_size; /* Number of items in variable part */
    digit ob_digit[1];
};

Hay PyObjectalgunos metacampos en la estructura que se usan para el recuento de referencias (recolección de basura), pero para hablar sobre esto, necesitamos un artículo separado. El campo en el que nos centraremos en esto ob_digity en un momento ob_size.

Descifrado `ob_digit`

ob_digitEs una matriz asignada estáticamente de unidad de longitud de tipo digit (typedef uint32_t). Como se trata de una matriz, ob_digites principalmente un puntero a un número y, por lo tanto, si es necesario, se puede aumentar utilizando la función malloc a cualquier longitud. De esta manera, Python puede representar y procesar números muy largos.

Típicamente, en lenguajes de bajo nivel como C, la precisión de los enteros está limitada a 64 bits, sin embargo, Python admite enteros de precisión arbitraria . Comenzando con Python 3, todos los números se presentan en el formulario bignumy están limitados solo por la memoria del sistema disponible.

Descifrado `ob_size`

ob_sizealmacena el número de elementos ob_digit. Python anula y luego usa el valor ob_sizepara determinar el número real de elementos contenidos en la matriz para aumentar la eficiencia de asignar memoria a la matriz ob_digit.

Almacenamiento

La forma más ingenua de almacenar números enteros es almacenar un dígito decimal en un elemento de la matriz, luego las operaciones, como la suma y la resta, se pueden realizar de acuerdo con las reglas de matemáticas de la escuela primaria.

Con este enfoque, el número 5238 se guardará así: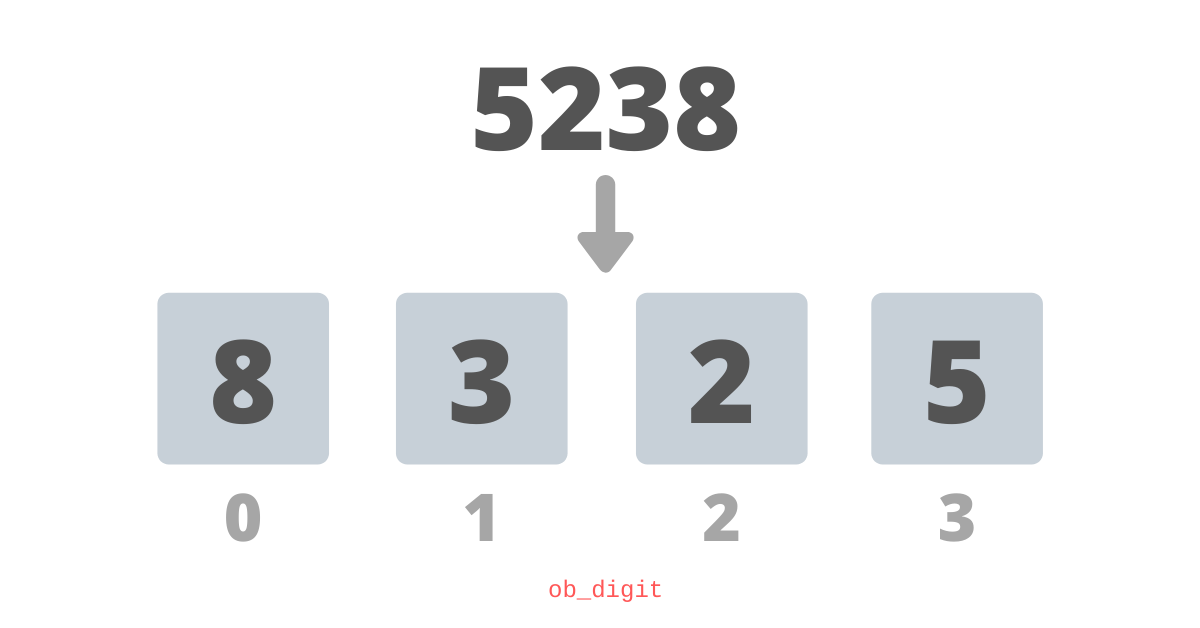

este enfoque es ineficiente, ya que usaremos dígitos de hasta 32 bits (uint32_t) para almacenar un dígito decimal, que, de hecho, varía de 0 a 9 y se puede representar fácilmente con solo 4 bits, porque al escribir algo tan versátil como python, el desarrollador del kernel debería ser aún más ingenioso.

Entonces, ¿podemos hacerlo mejor? Por supuesto, de lo contrario no habría publicado este artículo. Echemos un vistazo más de cerca a cómo Python almacena un número entero extra largo.

Camino de Python

En lugar de almacenar solo un dígito decimal en cada elemento de la matriz ob_digit, Python convierte los números del sistema de números con una base de 10 en números en un sistema con una base de 2 ³⁰ y llama a cada elemento como un dígito cuyo valor varía de 0 a 2 ³⁰ - 1.

En el sistema de números hexadecimales, la base 16 ~ 2 ⁴ significa que cada "dígito" del número hexadecimal varía de 0 a 15 en el sistema de números decimales. En Python, de manera similar, un "número" con una base de 2 ³⁰ , lo que significa que el número variará de 0 a 2 ³⁰ - 1 = 1073741823 en decimal.

De esta manera, Python usa eficientemente casi todo el espacio asignado de 32 bits por dígito, conserva los recursos y aún realiza operaciones simples como sumar y restar en el nivel de matemáticas de la escuela primaria.

Dependiendo de la plataforma, Python utiliza matrices enteras sin signo de 32 bits o matrices enteras sin signo de 16 bits con dígitos de 15 bits. Para realizar las operaciones que se discutirán más adelante, solo necesita unos pocos bits.

Ejemplo: 1152921504606846976

Como se mencionó, para Python, los números se representan en un ^sistema base 2 ³⁰ , es decir, si convierte 1152921504606846976 en un número base con 2 ³⁰ base , obtendrá 100.

1152921504606846976 = 1 * (2 ³⁰) ² + 0 * (2 ³⁰ ) ¹ + 0 * (2 ³⁰ ) ⁰

Dado que el ob_digitdígito menos significativo se almacena primero, se guarda como 001 como tres dígitos.

La estructura _longobjectpara este valor contendrá:

ob_size como 3
ob_digit como [0, 0, 1]

Creé una demostración REPL que mostrará cómo Python almacena un número entero dentro de sí mismo, y también se refiere a miembros de estructura como ob_size, ob_refcountetc.

Operaciones largas enteras

Ahora que tenemos una idea clara de cómo Python implementa enteros de precisión arbitraria, es hora de comprender cómo se realizan varias operaciones matemáticas con ellos.

Adición

Los enteros se almacenan "en números", lo que significa que la suma es tan simple como en la escuela primaria, y el código fuente de Python nos muestra que así es como se implementa la suma. Una función con un nombre x_adden un archivo longobject.cagrega dos números.

...
    for (i = 0; i < size_b; ++i) {
        carry += a->ob_digit[i] + b->ob_digit[i];
        z->ob_digit[i] = carry & PyLong_MASK;
        carry >>= PyLong_SHIFT;
    }
    for (; i < size_a; ++i) {
        carry += a->ob_digit[i];
        z->ob_digit[i] = carry & PyLong_MASK;
        carry >>= PyLong_SHIFT;
    }
    z->ob_digit[i] = carry;
...

El fragmento de código anterior se toma de una función x_add. Como puede ver, itera sobre un número por números y realiza la suma de números, calcula el resultado y agrega guiones.

Se vuelve más interesante cuando el resultado de la suma es un número negativo. El signo ob_sizees un número entero, es decir, si tiene un número negativo, entonces ob_sizeserá un signo menos. El ob_sizemódulo de valor determinará la cantidad de dígitos ob_digit.

Sustracción

Así como ocurre la suma, también tiene lugar la resta. Una función con un nombre x_suben el archivo longobject.cresta un número de otro.

...
    for (i = 0; i < size_b; ++i) {
        borrow = a->ob_digit[i] - b->ob_digit[i] - borrow;
        z->ob_digit[i] = borrow & PyLong_MASK;
        borrow >>= PyLong_SHIFT;
        borrow &= 1; /* Keep only one sign bit */
    }
    for (; i < size_a; ++i) {
        borrow = a->ob_digit[i] - borrow;
        z->ob_digit[i] = borrow & PyLong_MASK;
        borrow >>= PyLong_SHIFT;
        borrow &= 1; /* Keep only one sign bit */
    }
...

El fragmento de código anterior se toma de una función x_sub. En él, se ve cómo se produce la enumeración de números y se realiza la resta, se calcula el resultado y se distribuye la transferencia. De hecho, es muy similar a la suma.

Multiplicación

Y nuevamente, la multiplicación se implementará de la misma manera ingenua que aprendimos de las lecciones de matemáticas en la escuela primaria, pero no es muy eficiente. Para mantener la eficiencia, Python implementa el algoritmo Karatsuba , que multiplica dos números de n dígitos en pasos simples O (n ^log₂³ ).

El algoritmo no es simple y su implementación está más allá del alcance de este artículo, pero puede encontrar su implementación en funciones k_mul y k_lopsided_mulen el archivo longobject.c.

División y otras operaciones

Todas las operaciones en enteros se definen en el archivo longobject.c, son muy simples de encontrar y rastrear el trabajo de cada uno. Atención: una comprensión detallada del trabajo de cada uno de ellos llevará tiempo, así que pre-abastecerse de palomitas de maíz .

Python asigna previamente una pequeña cantidad de enteros en la memoria que van desde -5 a 256. Esta asignación se produce durante la inicialización, y dado que no podemos cambiar los enteros (inmutabilidad), estos números preasignados son singleton y se referencian directamente en lugar de asignarse. Esto significa que cada vez que usamos / creamos un número pequeño, Python en lugar de venderlo simplemente devuelve una referencia al número asignado previamente.

Dicha optimización se puede rastrear en la macro IS_SMALL_INTy la función get_small_intc longobject.c. Por lo tanto, Python ahorra mucho espacio y tiempo al calcular números enteros de uso común.

Este es el segundo artículo de la serie Python Internals. El primer artículo fue sobre cómo cambié mi versión de Python para hacerloambigua . Le ayudará a dar los primeros pasos para comprender el código fuente de Python y continuar el camino para convertirse en un desarrollador de kernel de Python.

Si desea ver más artículos similares, suscríbase a mi boletín y recíbalos directamente en su bandeja de entrada. Escribo sobre ingeniería, ingeniería de sistemas y un poco sobre programación todos los viernes. Envíeme un correo electrónico a @arpit_bhayani . Puede encontrar mis artículos anteriores en @ arpitbhayani.me / blogs .

Eso es todo. ¡Nos vemos en el curso !

¿Cómo se implementan los tipos enteros muy largos en Python?