👰🏼 🐝 👨‍🏫 Visualización de líneas de tensión y movimientos de cargas electrostáticas, simulación del movimiento planetario del sistema solar. 🐙 🤳🏾 🌤️

Hola, hoy quiero ofrecerte una ayuda visual para modelar algunos procesos físicos y mostrarte cómo obtener bellas imágenes y animaciones. Precaución muchas fotos.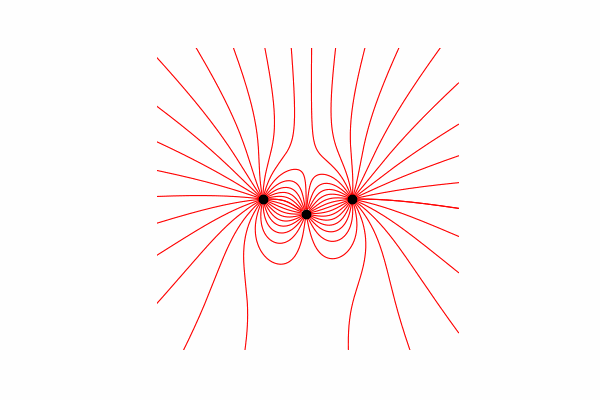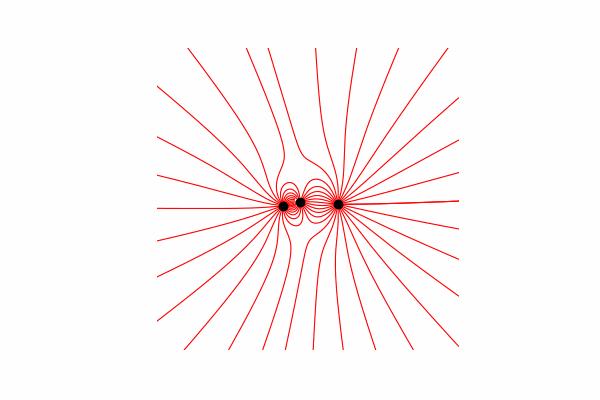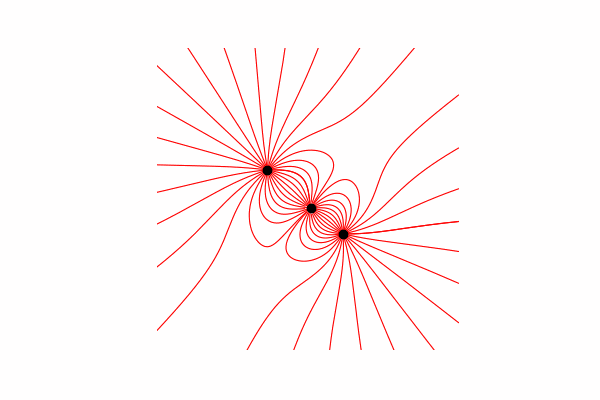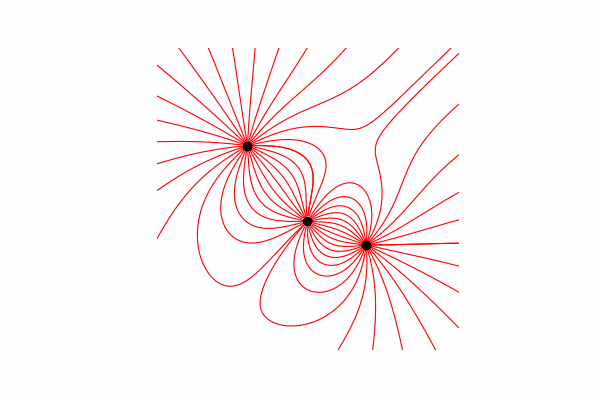

Todo el código se puede encontrar en google colab .

Teoría

Primero, necesitamos un pequeño mínimo teórico sobre este tema. Comencemos por comprender qué son las líneas de tensión y cómo contarlas. De hecho, estas líneas son la fusión de muchos vectores de tensión, que se pueden calcular de la siguiente manera: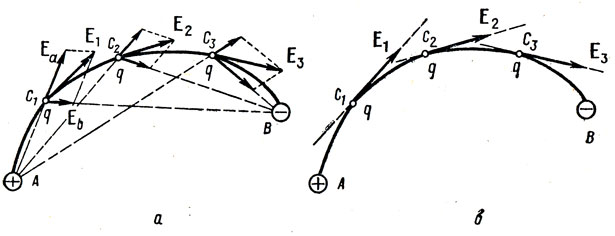

E = \frac{k * | q |}{r^{2}}

$E=\frac{k*|q|}{r^2}$ .

imagen

E método de cálculo

Calculé el vector de tensión a través de la similitud de triángulos, obteniendo proyecciones en los ejes x e y dx y dy, respectivamente.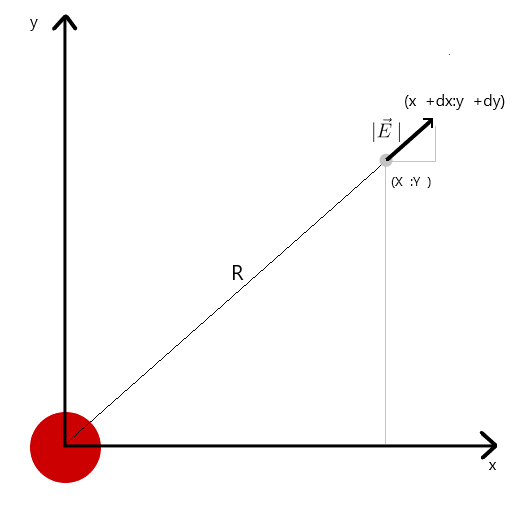

De la similitud se deduce que el radio del vector desde la carga hasta el punto en el espacio r y la longitud del vector de intensidad E es igual a la relación de las proyecciones de estos vectores (x1 y dx, respectivamente)

\frac{R}{E} = \frac{x}{d x} = \frac{y}{d y}

$\frac{R}{E}=\frac{x}{dx}=\frac{y}{dy}$ . Fórmula del vector resultante.

\vec{E} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{E}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{E}}_{i} |}{R_{i}} \end{matrix})

$\vec{E}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{E}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{E}_i|}{R_i} \end{array}\right) \qquad$
Con este conocimiento obtenemos el primer resultado.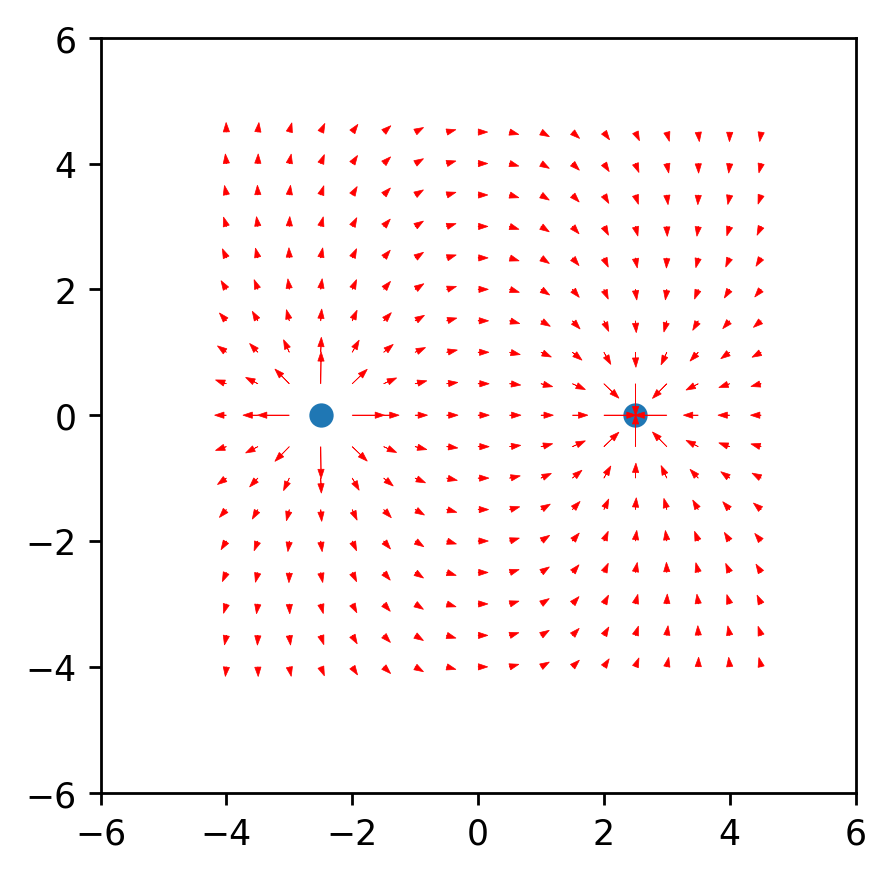

Función de cálculo de proyección

def E(q_prop, xs, ys, nq): #q_prop=[[xq1, yq1, q1, mq1, vxq1, vyq1], [xq2, yq2, q2, mq2, vxq2, vyq2] ... ] 
    l=1
    k=9*10**9
    Ex=0
    Ey=0
    c=0
    for c in range(len(q_prop)):#                
        q=q_prop[c]
        r=((xs-q[0])**2+(ys-q[1])**2)**0.5
        dEv=(k*q[2])/r**2
        dEx=(xs-q[0])*(dEv/r)*l
        dEy=(ys-q[1])*(dEv/r)*l

        Ex+=dEx
        Ey+=dEy
    return Ex, Ey

Método de construcción de línea

Primero debes decidir el punto de inicio y final desde donde irán la línea y el documento. El comienzo son puntos en un círculo con un radio r alrededor de la carga, y los puntos finales no están más que r separados de las cargas.

código para puntos de partida

theta = np.linspace(0, 2*np.pi, n)
mask=q_prop[ q_prop[:,2]>0 ]#    
for cq in range(len(mask)):
    qmask=mask[cq]
    xr = r_q*np.cos(theta)+qmask[0]# -    
    yr = r_q*np.sin(theta)+qmask[1]#

Por lo tanto, vale la pena decir que las líneas se construyen solo a partir de cargas positivas.

Y finalmente, la construcción de líneas. Para hacer esto, construimos la línea del vector de tensión en él desde el punto inicial, actualizamos el punto inicial al final de la línea construida y repetimos hasta que se alcanzan las condiciones finales mencionadas anteriormente.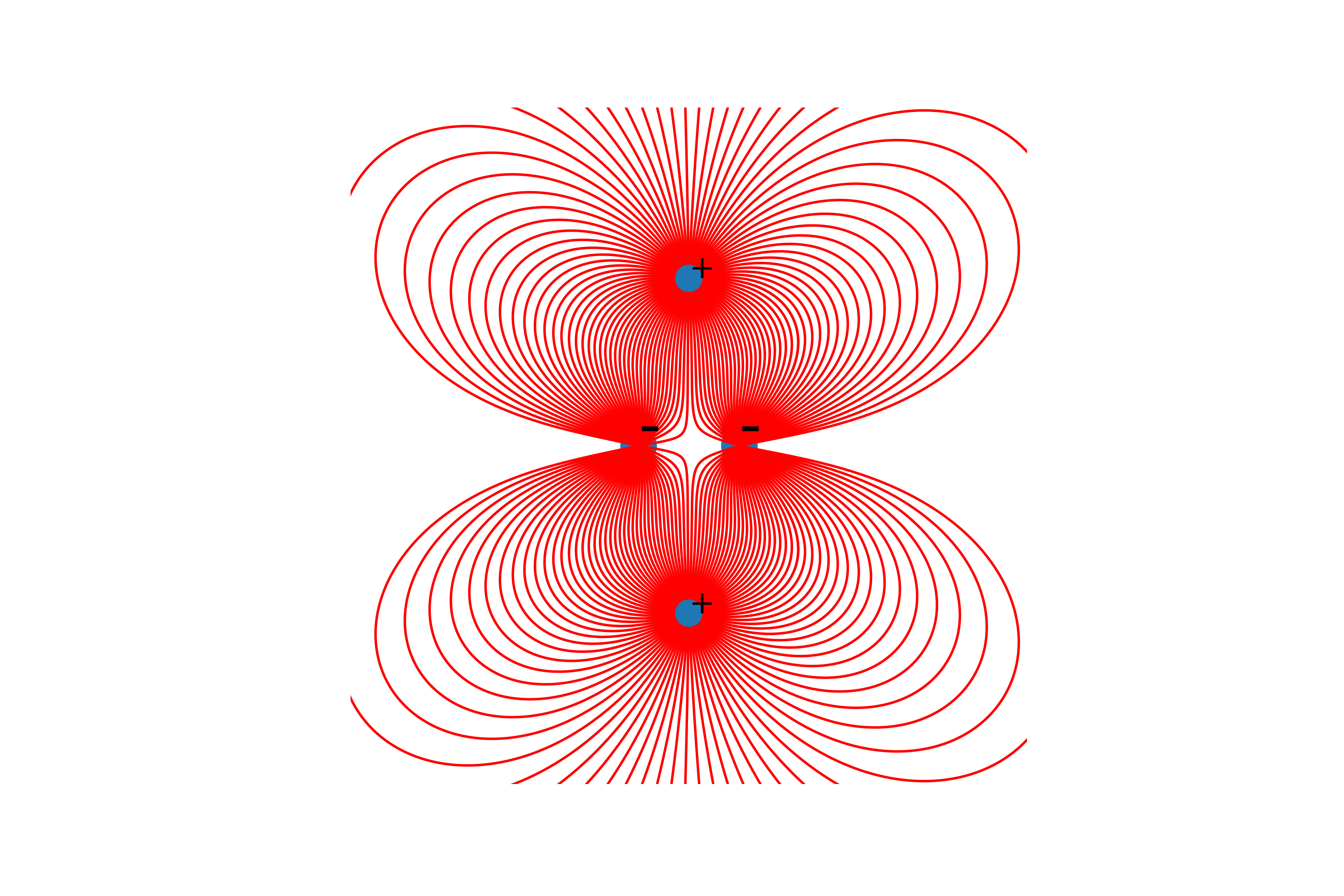

función de cálculo de coordenadas de línea

def Draw(size, q_prop,r_q, n):
  
  linen=np.empty((np.count_nonzero(q_prop[:,2]>0),n, 2000000), dtype=np.float64)
  linen[:] = np.nan
  theta = np.linspace(0, 2*np.pi, n)
  mask=q_prop[ q_prop[:,2]>0 ][ q_prop[q_prop[:,2]>0][:,3]==1 ]
  for cq in range(len(mask)):
    qmask=mask[cq]
    x11 = r_q*np.cos(theta)+qmask[0]
    x22 = r_q*np.sin(theta)+qmask[1]
    for c in range(len(x11)):

      xs=x11[c]
      ys=x22[c]

      lines=np.empty((2,1000000), dtype=np.float64)
      lines[:]=np.nan
      stop=0
      nnn=0
      
      lines[0][nnn]=xs
      lines[1][nnn]=ys
      while  abs(xs)<size+2 and abs(ys)<size+2: 
        nnn+=1

        for cq1 in range(len(q_prop)):
          q=q_prop[cq1]
          if ((ys-q[1])**2+(xs-q[0])**2)**0.5<r_q/2 :
            stop=1
            break
        if stop==1:
          break
        dx, dy = E1(q_prop,xs,ys)

        xs+=dx
        ys+=dy
        lines[0][nnn]=xs
        lines[1][nnn]=ys
       
      linen[cq,c,:]=lines.reshape(-1)

  return linen

Interacción entre cargos

Para reflejar su interacción, es necesario cambiar sus coordenadas y velocidad después de cada pequeño tiempo dt.

x + = \frac{E_{x} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{x} \cdot d t

$x+=\frac{E_x \cdot q \cdot dt^2}{2\cdot m} + v_x\cdot dt$

y + = \frac{E_{y} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{y} \cdot d t

$y+=\frac{E_y \cdot q \cdot dt^2}{2\cdot m} + v_y \cdot dt$

v_{x} + = \frac{E_{x} \cdot q \cdot d t}{m}

$v_x+= \frac{E_x \cdot q \cdot dt}{ m}$

v_{y} + = \frac{E_{y} \cdot q \cdot d t}{m}

$v_y+= \frac{E_y \cdot q \cdot dt}{ m}$

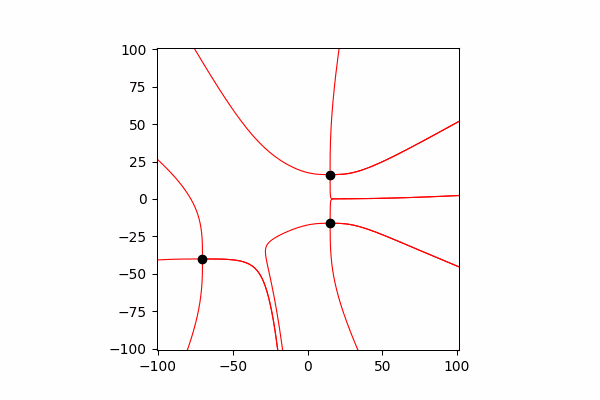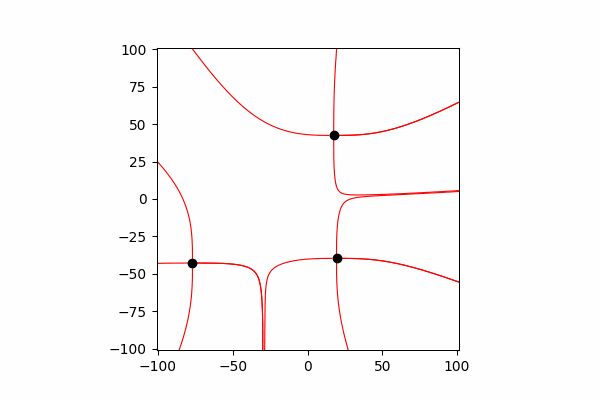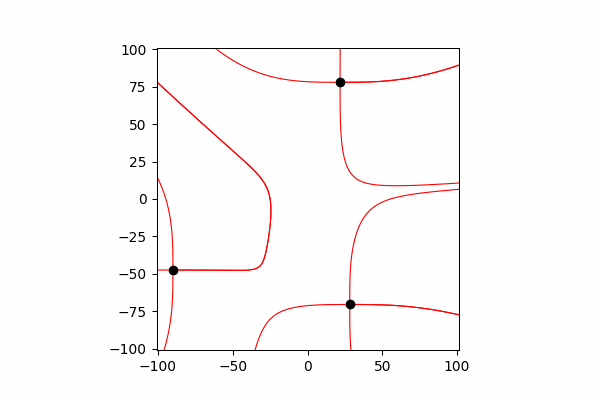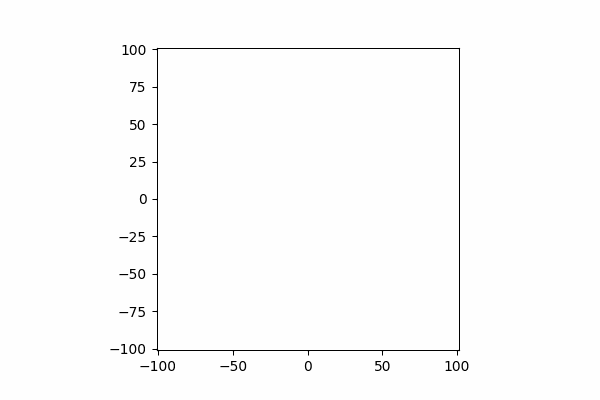
Función para actualizar coordenadas y proyecciones de velocidades de carga

def Update_all(q_prop):
  vx=0
  vy=0
  x=0
  y=0
  q_prop_1=np.copy(q_prop)
  for c in range(len(q_prop)):#         
    xs=q_prop[c][0]
    ys=q_prop[c][1]
    q =q_prop[c][2]
    m =q_prop[c][3]
    vx=q_prop[c][4]
    vy=q_prop[c][5]
    Ex, Ey= E(q_prop, xs, ys, c)

    x=(((Ex*q)/m)*dt**2)/2+vx*dt+xs
    y=(((Ey*q)/m)*dt**2)/2+vy*dt+ys
    vx+=((Ex*q)/m)*dt
    vy+=((Ey*q)/m)*dt
    #print(q_prop[c]-[x,y,q,m,vx,vy])
    q_prop_1[c]=[x,y,q,m,vx,vy]
  
  return q_prop_1#

Gravedad

Basado en el código existente, escribí un simulador que refleja los movimientos de los cuerpos bajo la influencia de la gravedad. Los cambios en el código son principalmente para la función de tensión ya que Ahora se considerará la aceleración utilizando una fórmula similar.

g = \frac{G * m}{r^{2}}

$g=\frac{G*m}{r^2}$

\vec{g} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{g}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{g}}_{i} |}{R_{i}} \end{matrix})

$\vec{g}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{g}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{g}_i|}{R_i} \end{array}\right) \qquad$

Los planetas comienzan desde el eje x a la distancia del perihelio y a la velocidad del perihelio. Todos los valores de los planetas y el sol (masa, distancia, extremidades) del directorio.

Animación para los primeros 4 planetas + sol.

A la espera de críticas y sugerencias. Adiós.

Visualización de líneas de tensión y movimientos de cargas electrostáticas, simulación del movimiento planetario del sistema solar.

Teoría

E método de cálculo

Método de construcción de línea

Interacción entre cargos

Gravedad

More articles: