La gente conoce los sistemas de recomendación. Factorización

El aprendizaje automático ha penetrado en nuestra vida cotidiana. Algunos ya no se sorprenden cuando se les informa sobre las redes neuronales en sus teléfonos inteligentes. Una de las grandes áreas de esta ciencia son los sistemas de recomendación. Están en todas partes: cuando escuchas música, lees libros, ves programas de televisión o videos. El desarrollo de esta ciencia tiene lugar en compañías gigantes como YouTube , Spotify y Netfilx . Por supuesto, todos los logros científicos en esta área se publican tanto en las famosas conferencias NeurIPS o ICML como en RecSys , un poco menos conocido .agudizado en este tema. Y en este artículo hablaremos sobre cómo se desarrolló esta ciencia, qué métodos se utilizan en las recomendaciones en ese momento y ahora, y qué matemáticas hay detrás de todo esto.

Me inspiró a escribir este artículo, trabajando en el StatML laboratorio en Skoltech relacionada con los sistemas de recomendación.

Por qué y para quién este artículo

¿Por qué puede ser esto importante para cada uno de nosotros? Echa un vistazo a la lista a continuación:

• Recomendaciones de video: YouTube, Netlix, HBO, Amazon Prime, Disney +, Hulu, Okko
• Recomendaciones de audio: Spotify, Yandex.Music, Yandex.Radio, Apple Music
• Recomendaciones de productos: Amazon, Avito, litros, MyBook
• Recomendaciones de búsqueda: Google, Yandex, Bing, Yahoo, Mail
• : Booking, Twitter, Instagram, ., , GitHub

, . , . , , YouTube.

( ), . , , . , ( ). -, . , -, , - . , . , , , , .

, , , , - . , (, , , ..). , .

, . : $$$U$ $$$I$ — . $$$r_{ui}$ $$$u$ $$$i$. , , , , . :

$$

$$\mathcal{D} = \{ (u, i) |\text{ if } \exists r_{ui}, u \in U, i \in I\}$$

$$$f$:

$$

$$f(u, i) = \hat{r}_{ui}\approx r_{ui}$$

, $$$r_{ui}$ 1 5 ( ) : 1 -1 ( / )

3 :

• Content-based (CB)
• Collaborative filtering (CF)
• Hybrid recommendations

. — , . : — , — , . . , : , ..

, . - , .

. , , , .

, , . . , , . .

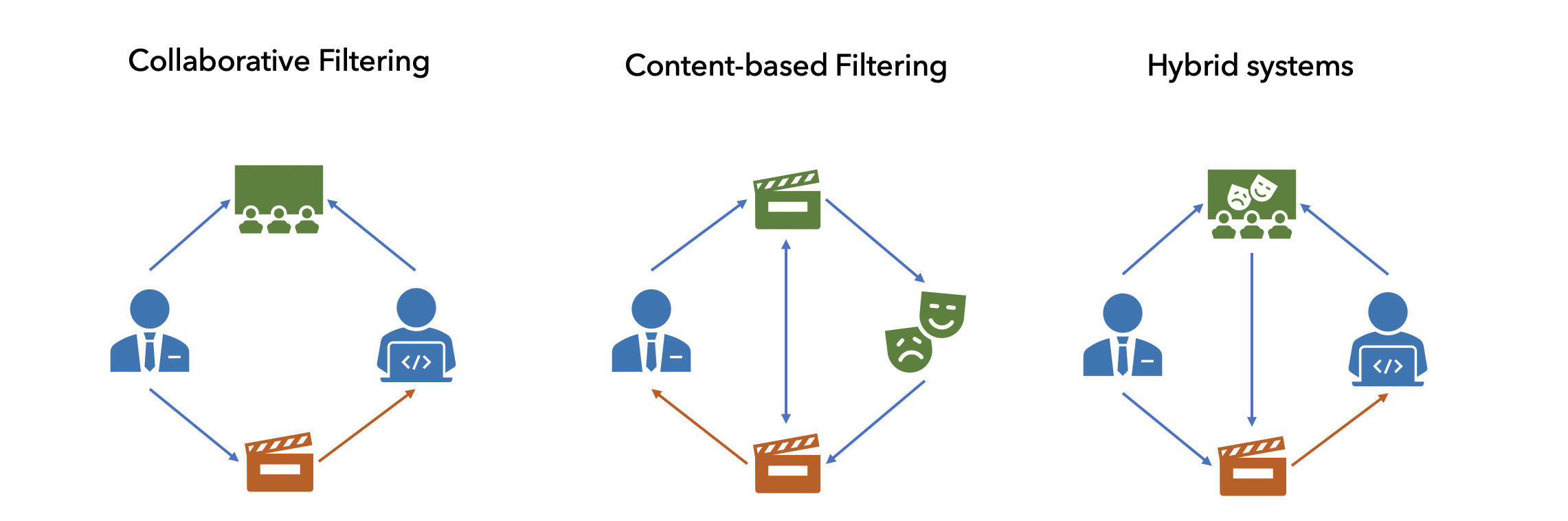
Matrix Factorization

, . : . .

• :
  
  • Singular Value Decomposition (SVD)
  • Singular Value Decomposition with implicit feedback (SVD++)
  • Collaborative Filtering with Temporal Dynamics (TimeSVD++)
  • Weighted Matrix Factorization (WMF or ALS)
  • Sparse Linear Methods (SLIM)
  • Factorization Machines (FM)
• :
  
  • Probabilistic Matrix Factorization (PMF)
  • Bayesian Probabilistic Matrix Factorization (BPMF)
  • Bayesian Factorization Machines (BFM)
  • Gaussian Process Factorization Machines (GPFM)

Singular Value Decomposition (SVD)

— SVD. $$$A$ $$$n \times m$, $$$n = |U|$, $$$m = |I|$. $$$\mathcal{D}$ $$$A_{ui} = r_{ui}$, . SVD , $$$A$ : $$$U,~\Sigma,~V$. $$$k$ , $$$A$.

$$

$$A = U \Sigma V^T, \quad\quad\quad\quad A \approx \hat{A} = \hat{U} \hat{ \Sigma } \hat{V}^T .$$

$$$Q$ $$$P$ . $$$A$ :

$$

$$P = (\hat{U} \hat{ \Sigma })^T, \quad\quad Q = \hat{V}^T, \quad\quad\quad\quad A \approx P^T \cdot Q .$$

:

$$

$$r_{ui} \approx \hat{r}_{ui} = p^T_u q_i .$$

, $$$p_u$ $$$q_i$ — $$$u$ $$$i$ - $$$k$. . . :

$$

$$\Theta = \{ p_u, q_i| u \in U, i \in I\} .$$

c :

$$

$$\sum_{(u, i) \in \mathcal{D}} (r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 = \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p^T_u q_i)^2 + \lambda\sum_{u \in U}\|p_u\|^2 + \lambda\sum_{i \in I}\|q_i\|^2 .$$

, , , , . $$$\hat{r}_{ui}$. (GD) (ALS). Habr- , . , , .

( SVD, SVD$$$_{bias}$). , , . . SVD . (bias):

$$

$$\hat{r}_{ui} =\mu + b_u + b_i + p^T_u q_i ,$$

$$$b_u$ — , $$$b_i$ — , $$$\mu$ — . :

$$

$$\Theta = \{ \mu, b_u, b_i, p_u, q_i| u \in U, i \in I\} .$$

SVD++

Factorization Meets the Neighborhood SVD . (explicit and implicit user feedback). $$$r_{ui}$, . . : $$$R(u)$ — ( ) $$$N(u)$ — ( ).

SVD++ :

$$

$$\hat{r}_{ui} =\mu + b_u + b_i + q^T_i \left( p_u + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) .$$

:

$$

$$\Theta = \{ \mu, b_u, b_i, p_u, q_i, y_i| u \in U, i \in I\} .$$

, $$$N(u)$ $$$R(u)$, .. $$$R(u) \subset N(u)$. (item-item recommendation).

Asymmetric-SVD

SVD++ . . :

$$

$$\hat{r}_{ui} = b_{ui} + q^T_i \left( |R(u)|^{-1/2} \sum_{j \in R(u)} (r_{uj} - b_{uj})x_j + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) ,$$

$$$b_{ui} = \mu + b_u + b_i$

TimeSVD++

TimeSVD++. (MovieLens, Netflix) , . , . Collaborative Filtering with Temporal Dynamics SVD++ :

$$

$$\hat{r}_{ui}(t) =\mu + b_u(t) + b_i(t) + q^T_i \left( p_u(t) + |R(u)|^{-1/2} \sum_{j \in R(u)} y_j \right) .$$

, :
Item bias: , ( 30 ) $$$b_{i,\text{Bin}(t)}$ , , $$$t$:

$$

$$b_i(t) = b_i + b_{i, \text{Bin}(t)}$$

Sesgo del usuario: al analizar los datos de Neflix, notamos que para cada usuario en promedio solo hay 40 días en los que coloca las calificaciones. Por lo tanto, actuaremos como con los productos y agregaremos nuestros propios parámetros$$$b_{u, t}$para cada usuario Agregamos una dependencia lineal del tiempo: introducimos un término adicional$$$\alpha_u$ con ratio de amortización:

$$

$$b_i(t) = b_i + \alpha_u \cdot \text{dev}_u(t) + b_{u, t} \quad\quad\quad\quad \text{dev}_u(t) = \text{sign}(t - t_u) \cdot |t - t_u|^{\beta}$$

.
Hay otras opciones sobre cómo agregar una dependencia de tiempo a los usuarios: se describe con más detalle en el artículo
Incorporaciones de usuarios: agregaremos un truco similar para cada componente de nuestra representación latente$$$p_u(t) = (p_{u1}(t), \dots, p_{uf}(t))^T$:

$$

$$p_{uk}(t) = p_{uk} + \alpha_{uk} \cdot \text{dev}_u(t) + p_{uk, t}.$$

Factorización de matriz ponderada (WMF) y mínimos cuadrados alternos (ALS)

, SVD, . SVD++. — Weighted Matrix Factorization (WMF). ($$$\hat{r}_{ui} = p^T_u q_i$), . $$$r_{ui}$, (.. $$$(u, i) \notin \mathcal{D}$) 0. $$$(u, i)$ $$$c_{ui}$, $$$r_{ui}$. , . - . YouTube , . , , , . , , , :

$$

$$\sum_{(u, i)} c_{ui}(r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 .$$

: $$$c_{ui} = 1 + \alpha r_{ui}$. : $$$r_{ui}>0$ $$$r_{ui} = 0$. $$$\alpha$ $$$\alpha = 40$ .

, (ALS) . WMF, ALS, .

Fast Alternating Least Squares

ALS , eALS . , . , . .

, $$$c_{ui}$ ALS :

$$

$$c_{ui} = c_i + \alpha r_{ui}, \quad\quad\quad\quad c_i = c_0 \frac{f_i^{\beta}}{\sum_{j \in I} f_j^{\beta}} ,$$

$$$c_0$ $$$\beta$, .

Sparse Linear Methods (SLIM)

Sparse Linear Methods (SLIM) . , SVD . . SLIM :

$$

$$\hat{a}_{ui} = a^T_u w_i \quad\quad\quad\quad \hat{A} = AW$$

$$$W \in \mathbb{R}^{m \times m}$. : $$$W \geq 0$ $$$\text{diag}(W) = 0$. :

$$

$$\frac{1}{2}\|A - AW\|^2_F + \frac{\beta}{2}\|W\|^2_F + \lambda\|W\|_1$$

$$$W$ .

Factorization Machines (FM)

, Factorization Machines (FM). , ( 2- ). :

$$

$$\hat{r}(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{i=j+1}^{n} v^T_i v_j ~ x_i x_j, \quad\quad\quad\quad w_0 \in \mathbb{R} ~~~ w \in \mathbb{R}^n ~~~ V \in \mathbb{R}^{n \times k} .$$

(SGD) ( ). , $$$x$ $$$(u, i)$. . , — . — ( ). ( ).

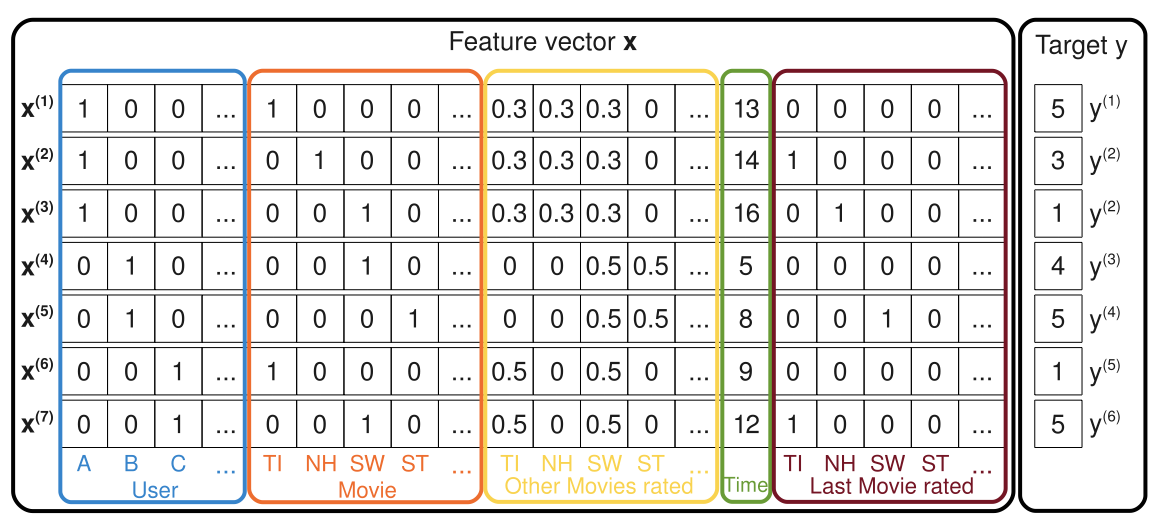
, SVD, SVD++ — FM. SVD , :

$$

$$n = | U \cup I |, \quad\quad\quad x_j = \delta (j = u ~\lor~ j = i) .$$

$$$\delta$ — . .. $$$x$ $$$u$ $$$i$. FM :

$$

$$\hat{r}(x) = w_0 + w_u + w_i + v^T_u v_i .$$

, $$$x$: , . , , , , , , . .

Probabilistic Matrix Factorization (PMF)

, , , .

(PMF), . , SVD: $$$p_u$ $$$q_i$ — . , :

$$

$$p(r | P, Q, \sigma) = \prod_{(u, i) \in \mathcal{D}}\mathcal{N}(r_{ui}| g(p_u^Tq_i), \sigma^2) ,$$

$$$\mathcal{N}$ — , a $$$g(x) = \frac{1}{1 + e^{-x}}$ — (). , , :

$$

$$p(P| \sigma_p) = \prod_{u \in U} p(p_u| 0, \sigma^2_p \mathbf{I}), \quad\quad\quad\quad p(Q| \sigma^2_q) = \prod_{i \in I} p(q_i| 0, \sigma_q^2 \mathbf{I}) .$$

( ) , :

$$

$$\frac{1}{2} \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p_u^T q_i)^2 + \frac{\lambda_p}{2} \sum_{u \in U} \|p_u\|^2 + \frac{\lambda_q}{2} \sum_{i \in I} \|q_i\|^2 ,$$

$$$\lambda_p = \frac{\sigma_p}{\sigma}$ $$$\lambda_q = \frac{\sigma_q}{\sigma}$ — . , SVD , .

Constrained PMF

PMF Constrained PMF. , SVD SVD++. , , $$$p_u$ :

$$

$$p_u + \frac{\sum_{i \in R(u)} y_i}{|R(u)|} ,$$

$$$R(u)$ — , $$$u$.

Bayesian Probabilistic Matrix Factorization (BPMF)

PMF BPMF. PMF , , . :

$$

$$p(P| \mu_p, \Lambda_p) = \prod_{u \in U} p(p_u| \mu_p, \Lambda_p) ,\quad\quad\quad\quad p(Q| \mu_q, \Lambda_q) = \prod_{i \in I} p(q_i| \mu_q, \Lambda_q) .$$

$$$\Theta_p = \{ \mu_p, \Lambda_p \}$ $$$\Theta_q = \{ \mu_q, \Lambda_q \}$ - $$$\Theta_0 = \{ \mu_0, \nu_0, W_0 \}$. , .

Bayesian Factorization Machines (BFM)

, Bayesian, . , $$$\Theta = \{ w_0, w_i, v_i\} .$ , - . : $$$\Theta_H = \{ \lambda_{\theta}, \mu_{\theta} | \theta \in \Theta \}$. .

Gaussian Process Factorization Machines (GPFM)

GPFM . $$$f$ $$$\theta$. $$$\theta_u$ , , :

$$

$$\hat{r}_{ui} = f(q_i, \theta_u)$$

, . , $$$f$ , . , , , .

.

: Bayesian Personalized Ranking (BPR)

BPR , "". , BPR — , , Bayesian Personalized Ranking. . , , $$$i$ $$$j$ $$$u$. $$$(u, i)$ $$$r_{ui}$ $$$(u, i, j)$ $$$i$ $$$j$ ((+) $$$i$ , $$$j$ (-) ). $$$\mathcal{D}_S$. . ( personalized ):

$$

$$p(i <_u j | \Theta) = \sigma(\hat{r}_{uij}(\Theta)) ,$$

$$$\sigma$ — , a $$$\hat{r}_{uij}$ — . (MLE), , :

$$

$$\min_{\Theta} \sum_{(u, i, j) \in \mathcal{D}_S}\ln{\sigma(\hat{r}_{uij})} - \lambda \|\Theta\|^2$$

(SGD):

$$

$$\Theta \leftarrow \Theta + \alpha\left(\frac{e^{-\hat{r}_{uij}}}{1 + e^{-\hat{r}_{uij}}} \cdot \frac{\partial}{\partial \Theta}\hat{r}_{uij} + \lambda \Theta \right)$$

, . , , . SVD:

$$

$$\hat{r}_{uij} = \hat{r}_{ui} - \hat{r}_{uj} \quad\quad\quad\quad \hat{r}_{ui} = p_u^T q_i$$

:

$$

$$\frac{\partial}{\partial \Theta}\hat{r}_{uij} =\begin{cases} (q_{ik} - q_{jk})~~~\text{if } \theta = p_{uk}\\ p_{uk}~~~~~~~~~~~~~~~\text{if } \theta = q_{ik}\\ -p_{uk}~~~~~~~~~~~~\text{if } \theta = q_{jk} \end{cases}$$

BPR ( ) , . , . . , (pairwise approach) (pointwise approach). . , 5 , . , , . — BPR - , . , .

Show must go on

Esta vez discutimos muchos métodos de Factorización en sistemas de recomendación, pero las Redes Gráficas y Neuronales , que también tienen muchas cosas interesantes , permanecieron intactas .