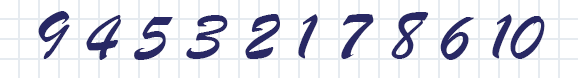May turned out to be cold, the heating was turned off, and the computing (and heating) powers were none, but they were idle. So why not load them with something useless , which will warm and entertain.But I'll start from afar. The other day, I came across a problem for a high school with the following wording: “Several consecutive positive integers were written out in a row in such a way that the sum of every three consecutive numbers is divided entirely by the leftmost number of this triple. "What is the maximum number of numbers that could be written out if the last line number is odd?”With this restriction, it is easy to prove that in each triple of odd numbers there will be more than even numbers. And since the difference between them cannot be more than one, the maximum length of the sequence is limited to five numbers. And as an example, we can give the sequence 4 5 3 2 1 .Detailed proof can be found here.But what if we remove the indicated restriction on the oddness of the last number? Then on the right you can add the numbers 7 6 8 , expanding the sequence to eight numbers. You can also add a dozen, and attach the missing nine to the left. Well, and probably this will not be the only and not the longest permutation.Actually, trying to reason logically, I did not find evidence of the limitations of such sequences and decided to involve a calculator in the home heater for analysis . Rough exhaustive search of all N ! options quickly showed the failure of the method, but directional enumeration allowed significant progress, and the result was both expected and unexpected at the same time.It turned out that for all N up to and including 29, such permutations of numbers from 1 to N are indeed found, however, for lengths 27 and 29 in a single variant. But then there are gaps. For permutations with sizes 30, 31, 32, and 33, there are no solutions; for the number 34, there is one.such33 23 10 13 7 6 1 29 27 2 25 21 4 17 15 19 11 8 3 5 31 9 22 14 30 26 34 18 16 20 12 28 32 24
Then again, two spaces. For values 37 and 38, such sequences are not single, and then a failure. I was even desperate, the next ten turned out to be completely empty, but luck smiled, for N = 51 the necessary permutation is still found.here she is46 45 1 44 49 39 10 29 21 37 5 32 23 41 51 31 20 11 9 2 43 35 8 27 13 14 25 3 47 40 7 33 16 17 15 19 26 50 28 22 6 38 34 4 30 18 42 48 36 12 24
There are even two of them, but they intersect for the most part.Further, emptiness is again planned, at least for the numbers 52 and 53 there are no solutions, but I did not look further. Nevertheless, with each step, the waiting time is growing exponentially, and the house has already become much warmer, I decided to stop there for now.If you reduce the found number of possible options in one table, you can build the following chart
Well, yes, there is something to meditate on.In the original problem, there was no requirement to start the natural series from one. The main thing is that all numbers from a to b are found in the sequence. But I tried, it only gets worse, there are even fewer options. Which, in fact, is explainable. The larger the number is in the left position of the triple, the lower the multiplicity can be obtained by the sum of the other two, i.e. the less options available. Well, the question of the upper limit of the lengths of such sequences remains open. With the growth of dimensionality, the probability of success is clearly reduced, but is it nullified? Or further, they will, albeit rarely, encounter such (un) interesting permutations.Finally, perhaps you can bring the code of the heating program,true he is on Haskellimport Data.List (delete)
import Control.Parallel.Strategies
import System.Environment
pvc :: Int -> Int -> [Int] -> [[Int]]
pvc a b [] = [[a,b]]
pvc a b xs = [a:ys |
x <- xs,
mod (a + b + x) a == 0,
ys <- pvc b x (delete x xs)]
gen :: Int -> [[[Int]]]
gen n =
let ab = [(a, b) | a <- [1..n], b <- delete a [1..n]]
in map hlp ab `using` parList rseq
where
hlp (a,b) = pvc a b $ delete a $ delete b [1..n]
main = do
[n] <- getArgs
print $ concat $ gen $ read n