Guilloche is a characteristic pattern on paper money and other securities. A detailed story about them with a digression into history can be found in the previous article . A drawing algorithm that builds guilloches by points was also given there.Quite useless, it should be noted if we draw them not just for fun, but for practical purposes - for example, to add those very securities to the design. Thousands of points will only slow down the editor, but it won’t be able to display the result anyway - instead of real continuous lines, there will be some kind of result of averaging the points, made as God would put a soul on.Therefore, the time has come to think about another algorithm - which would immediately give vectors. Since the common editors for curved lines only offer interpolation by Bezier curves, we will focus on them.The algorithm, in fact, is simple - and much simpler than described in the first part. We take two envelope curves, set the number of waves that should fit into 360 degrees, we estimate at what angle and with what curvature a real guilloche should go from the current point to the next, and interpolate it with four Bezier curves.Here is a program in Asymptote, which is extremely convenient for such things.import graph;
size(1000,1000);
xaxis(ticks=Ticks);
yaxis(ticks=Ticks);
defaultpen(2);
var zero = (0,0);
real tens(bool at_top, real angle)
{
return angle/180;
}
guide wave(path top, path bottom, int parts, real offset)
{
guide w;
real step = 1/parts;
real half = step/2;
pair[] top_pt;
pair[] bot_pt;
pair[] top_dir;
pair[] bot_dir;
real[] top_angle;
real[] bot_angle;
for(int i: sequence(0,parts-1))
{
real rel = i*step + step*offset;
real top_time = reltime(top, rel);
real bot_time = reltime(bottom, rel+half);
top_pt[i] = point(top, top_time);
bot_pt[i] = point(bottom, bot_time);
top_dir[i] = dir(top, top_time);
bot_dir[i] = dir(bottom, bot_time);
}
for(int i: sequence(0,parts-1))
{
int prev = i == 0 ? parts-1 : i-1;
int next = i == parts-1 ? 0 : i+1;
var v1 = bot_pt[i] - top_pt[i];
var v2 = bot_pt[prev] - top_pt[i];
var a = degrees(v2) - degrees(v1);
top_angle[i] = a<0 ? 360+a : a;
v1 = top_pt[i] - bot_pt[i];
v2 = top_pt[next] - bot_pt[i];
a = degrees(v2) - degrees(v1);
bot_angle[i] = a<0 ? 360+a : a;
}
for(int i: sequence(0,parts-1))
{
int next = i == parts-1 ? 0 : i+1;
var l1 = length(top_pt[i]--bot_pt[i]);
pair ctl1 = top_pt[i] + top_dir[i] * tens(true, top_angle[i]) * l1;
pair ctl2 = bot_pt[i] - bot_dir[i] * tens(false, bot_angle[i]) * l1;
w = w .. top_pt[i] .. controls ctl1 and ctl2 .. bot_pt[i];
var l2 = length(bot_pt[i]--top_pt[next]);
ctl1 = bot_pt[i] + bot_dir[i] * tens(false, bot_angle[i]) * l2;
ctl2 = top_pt[next] - top_dir[next] * tens(true, top_angle[next]) * l2;
w = w .. bot_pt[i] .. controls ctl1 and ctl2 .. top_pt[next];
}
return w;
}
void repeat(int count, path top, path bottom, int parts)
{
real step = 1/count;
for(int i: sequence(0, count-1))
{
draw(wave(top, bottom, parts, step*i));
}
}
path normalize(path p)
{
var min = min(p);
var max = max(p);
var top_center = min + ((max.x-min.x)/2, (max.y-min.y)/2);
return scale(20*1/(max-min).x)*shift(zero - top_center)*p;
}
path top = (338.499521684,-159.274266483)
..controls (327.252951684,-158.148796483) and (323.448961684,-145.618286483) .. (318.743661684,-137.260595483)
..controls (309.897671684,-123.808725483) and (292.025851684,-123.657732483) .. (278.251471684,-118.807470483)
..controls (272.669581684,-117.510629483) and (268.731931684,-109.221757483) .. (274.571781684,-105.645360483)
..controls (281.545351684,-101.031122483) and (290.488261684,-97.7906864833) .. (293.317871684,-89.0437964838)
..controls (296.611021684,-81.8498064838) and (293.894071684,-73.5853264838) .. (295.556161684,-66.3445764838)
..controls (299.563831684,-59.7686064838) and (308.181311684,-64.5344964838) .. (312.903811684,-67.4344264838)
..controls (325.368171684,-74.9872364838) and (341.157891684,-80.6126364838) .. (355.257331684,-73.9383264838)
..controls (363.506651684,-70.9246164838) and (370.115991684,-63.9703964838) .. (378.731941684,-62.0926264838)
..controls (384.688491684,-61.4010364838) and (389.980631684,-67.6129964838) .. (387.306161684,-73.3211464838)
..controls (385.256921684,-82.8346964838) and (388.441441684,-93.9447564833) .. (397.757331684,-98.3016064833)
..controls (403.144721684,-101.085582483) and (412.671611684,-104.606352483) .. (410.331551684,-112.414892483)
..controls (406.654931684,-119.718595483) and (396.921641684,-119.937732483) .. (390.144051684,-122.524267483)
..controls (378.065751684,-125.483516483) and (364.313841684,-130.717262483) .. (359.884541684,-143.562216483)
..controls (356.731021684,-151.157386483) and (350.818391684,-160.192046483) .. (341.435061684,-159.293796483)
..controls (340.456461684,-159.306096483) and (339.478031684,-159.281196483) .. (338.499521684,-159.274296483)
--cycle;
top = normalize(top);
bottom = scale(0.5)*top;
top = ellipse(zero, 4, 6);
bottom = ellipse(zero, 2, 3);
top = circle(zero, 5);
bottom = circle(zero, 3);
repeat(12, top, bottom, 8);
The most understandable case is when the sinusoids are located between two circles.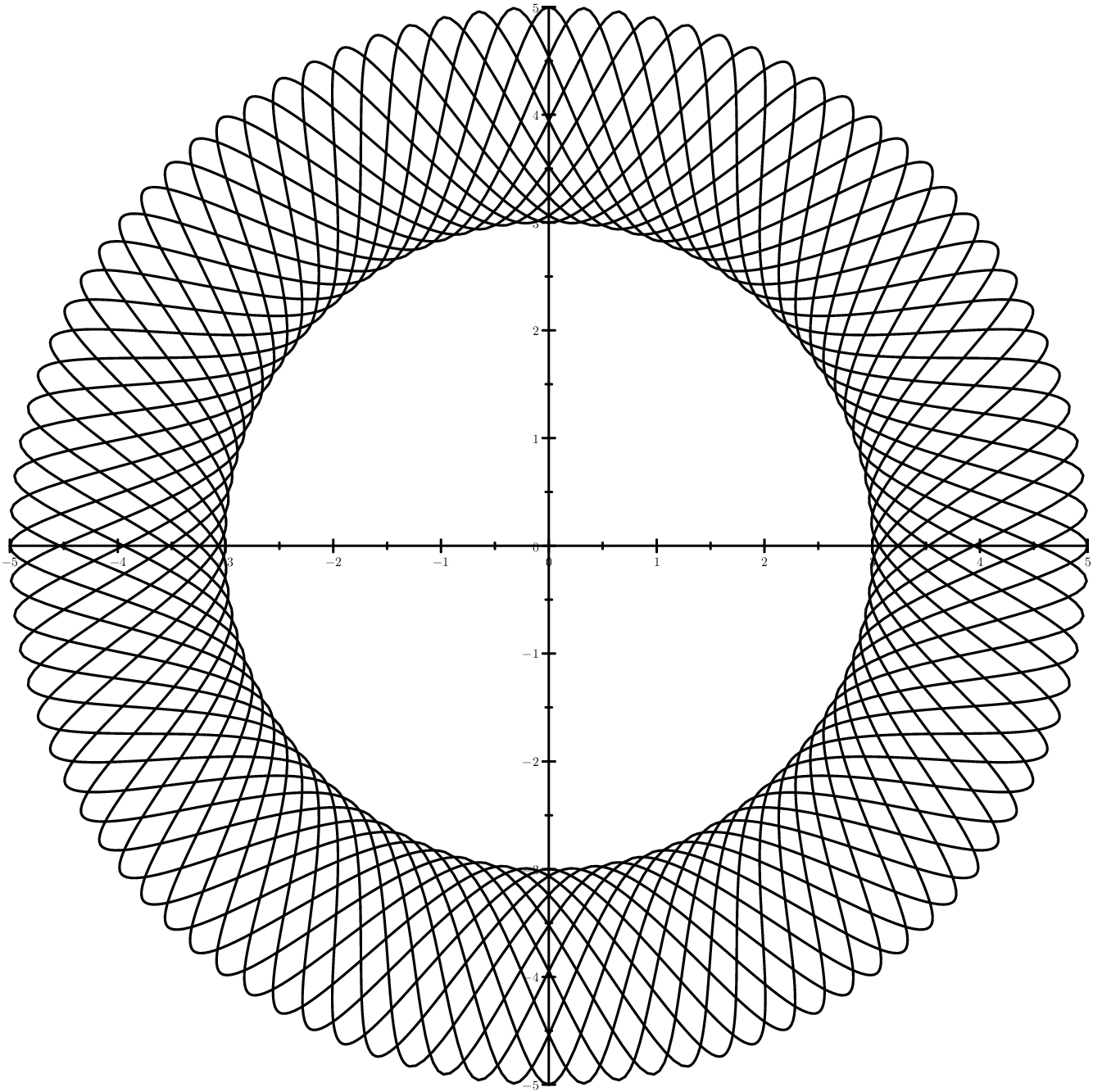
The case is more cunning - ellipses instead of circles.
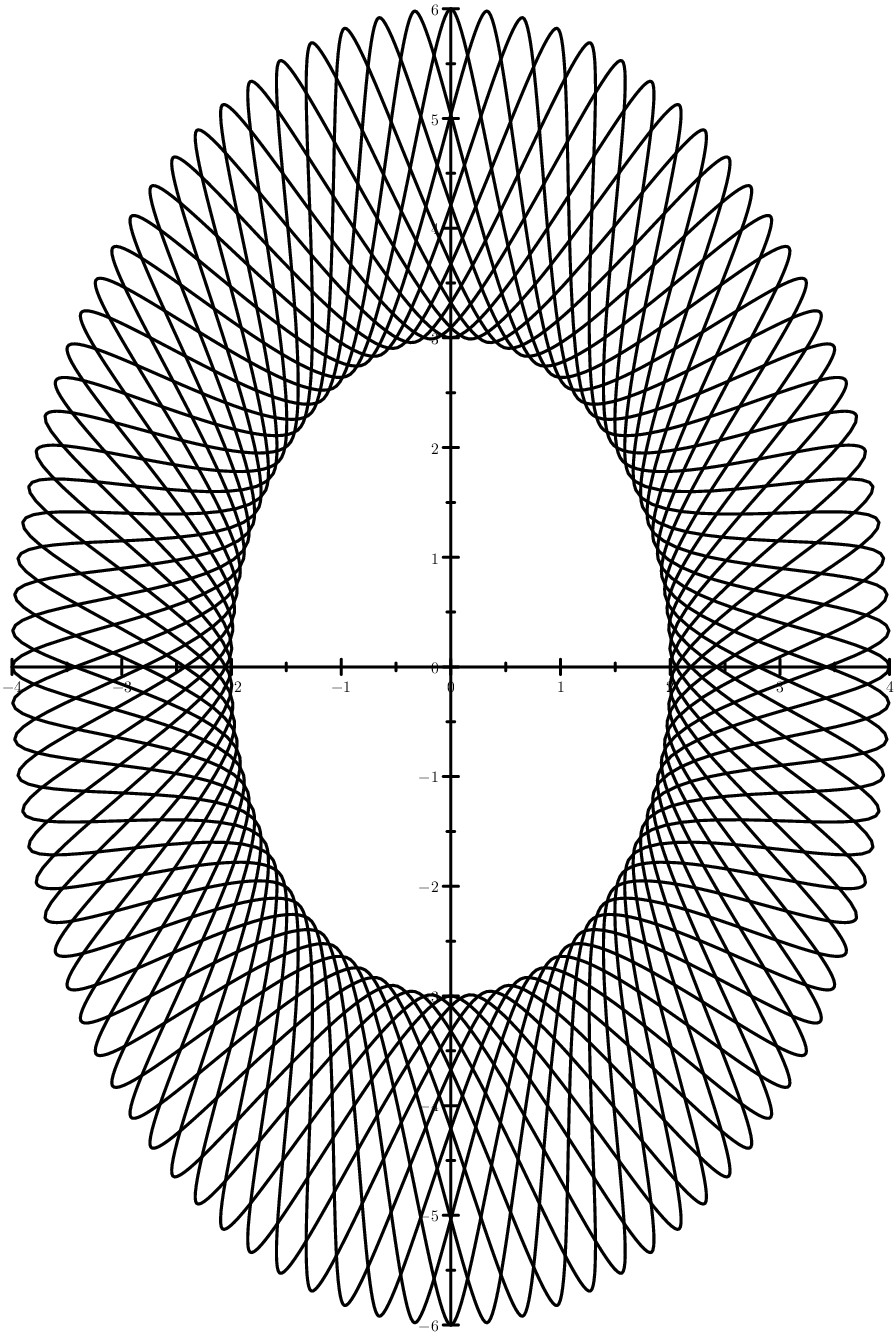And a picture close to industrial use: guilloche, forming a kind of artistic outlet.
Here the result, however, is not perfect. First, the tens function had to be adjusted so that it always returned a constant “tension” of 0.5. And secondly, the curves are not very symmetrical, and in the left part near the X axis they are somehow confused. Of course, all this can be corrected by hand, especially if you make banknotes for the state and have very qualified artists, but you can try and increase the accuracy of the calculations, because they obviously go astray at some points where the curvature of the envelopes changes sharply.Since the guilloche is interpolated, the question arises: do they coincide with, so to speak, “real”, that is, drawn by points. Being new to differential geometry, I find it difficult to say, but rather “no” than “yes”.But who really sees the difference?And the practical benefit is undeniable - with a couple of dozens of Bezier curves, it’s much easier to work than with a thousand dots, and they offer much more design possibilities.In addition, this algorithm can also be improved. Two options immediately suggest themselves:a) specify a different number of points on the external and internal curve, then the effect of grinding the pattern closer to the center will not be created, as in the examples with a circle and an ellipse.b) place the points on the envelopes not evenly, but, for example, making them more often, less often, which will add a new dimension to the pattern.