Imagine the situation - you are buying a car, and you are offered two options: pay by installments for several months or pay off the entire amount immediately and at a small discount. Which would be more profitable?Or, for example, you want to place a contribution for a year. You can put for the whole term at a high percentage or for individual short periods at a lower. Which is better and how much?All answers are under a cat. And welcome to a world where time is always money. You knew about it before, but now - in detail and with examples.My name is Maria Abrashkina, I am a mathematician and Product Owner in the portfolio risk calculation team. And also one of the authors of the video course on financial mathematics (Part 1 - Types of interest calculation , Part 2 - Discounting , Part 3 - Forward interest rates ). In this post I will talk about the value of money, interest rates and bonds . This knowledge will help you in future to make financial decisions based on accurate calculation, using simple mathematics.#1. The time value of money. Types of interest accrual
First, let's talk about what is the time value of money, or Time Value of Money (TVM) , why money has value and what types of interest exist.The picture below shows a list of movies with maximum box office.Can we compare them by these numbers? Given that the films were released in different years, it is unlikely that such a comparison will be correct. How to beLet's look at a simpler example. Suppose you have a thousand rubles, and I ask you for this amount in debt. How much do you want me to give you in a year? Perhaps you will think that for this thousand rubles you can now buy a bottle of delicious wine or something else. You can also assume that after a year for the same thousand rubles, you are unlikely to be able to buy this product because of inflation. In addition, there is a risk that I will not return the money. Therefore, most likely, you will want compensation for the fact that you will not buy a bottle of wine or any other thing. You also need an incentive to justify the risk that I may not return the money to you. You will probably require me to return the money with some kind of allowance, that is, with a percentage.So, money has value because its owner wants compensation for the fact that he cannot buy any product or service, and for the risk that he carries, giving money in debt.
In the language of mathematics, it will look like this:PV = 1000Now you give me a thousand rubles. Denote it as PV (Present Value). Let's say the rate (r)is 5%, and you give me the money for a period of one year. Then returning the money FV (Future Value), I have to add 50 rubles to the original amount.If you write this formula in general, then the future value is equal to the amount of debt multiplied by one plus the interest rate.But what if interest is calculated more than once a year, but more often? Or what if interest is accrued for two, three, ten years? In this case, we always need to clarify how interest is accrued, at the end of the term or with some frequency and for how many years.Simple interest
Consider the example where interest is accrued at the end of the deposit term. The future value will be equal to the current value plus the current value multiplied by the annual interest rate. The annual interest rate will be added to the amount of our deposit as many times as for how many years we have made a contribution.Result - the current value multiplied by the sum of the unit plus the interest rate (r)multiplied by the number of years of the contribution (T). This method of calculating interest is called simple interest .If the interest rate is charged every year, then the formula will look different.
Consider the situation with the accrual over a period of several years. We believe that the current interest rate throughout the period will be the same. Then the formula takes the following form: the current value multiplied by the sum of the unit plus the interest rate, then again by the sum of the unit and the interest rate, etc. Multiply so many times by how many years the contribution has been made. In general, the formula will look like this:Please note that if in the first case, the interest amount was added to our deposit every year (as in the first example, where 50 rubles were added to the deposit amount), then in the case of an annual charge of 50 rubles added in the first period, we charge each time percent.It is always important to pay attention to how interest is calculated. Interest can be accrued not only once a year, but also once every six months, every day. And in principle, nothing prevents us from charging these percentages continuously.Continuous interest accrual
Let's look at how the formula for calculating interest will look like more than once a year. In this case, the future value will be equal to the current value multiplied by the amount of one plus the annual interest rate divided by the number of accrual periods in the year (n)in degree nT. If accruals are made every six months, then n=2if every day, then n=365.What will the formula look like if we want to accrue interest continuously? Here you have to remember school math. The formula will be as follows:In order to bring our limit to some convenient form, we need to make a substitution. As a result, we get the following:Given that our limit is equal to the Euler number (e = 2.71), our formula is converted into a very simple expression. The current value of our contribution is multiplied by the exponent, which is raised to the extent represented by the product of the interest rate and the number of years on which our interest is accrued.Let's compare how payments look depending on the frequency of accruals. The table shows the future value of the contribution of one hundred thousand rubles, which is put for ten years at a rate of twenty percent.As you can see, the depositor will receive 300 thousand rubles in the event that accruals are made at the end of the deposit term.Thus, the amount of the deposit when calculating interest annually doubles the amount of the deposit when paying interest once at the end of the term.
If accruals are made continuously, then the deposit amount is more than 700 thousand rubles against 300 thousand rubles with a simple interest calculation.The graph below clearly shows how the total amount of deposits grows with different methods of calculating interest.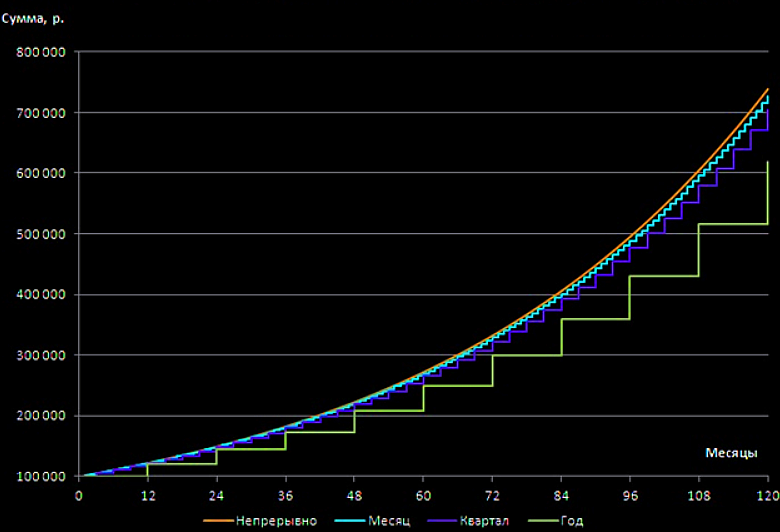
From this it is necessary to conclude:when choosing a contribution, it is important to look not only at the size of the interest rate, but also at the frequency of interest accrual. A high interest rate is not always truly beneficial.
Therefore, before making your choice, it makes sense to do small calculations to find out the total amount of the contribution under the given conditions.# 2 Discounting (helps to understand which is better: take an installment plan or pay now at a discount)
We examined what are the rates and what are the methods of calculating interest. If interest is paid at the end of the term of the deposit, interest is called simple , if interest is paid at some periodicity, then such interest is called complex .Let's solve the inverse problem. Suppose we know how much we will be paid in the future (for example, someone promised us a payment for some product). We also know what the interest rate is now. How do we calculate the current price of this product?As mentioned earlier, the future value of the payment amount will be equal to the current value multiplied by one plus the interest rate. If we express the current value from this formula, then it will equal the future value divided by one plus the interest rate.If interest is accrued with some periodicity, then in general terms the formula looks like this:T- this is the number of periods for paying interest charges. This process of dividing the future value by one, plus the interest rate, is to a degree Tcalled discounting . And the factor, the unit divided by the sum of the unit plus rthe power T, is called the discount coefficient .Let's get back to the task of which premium is better to choose. Depending on the bonus method, the amount of payments may vary. However, it is not always obvious which method is preferable. To give the correct answer, it is necessary to solve a mathematical problem. Suppose we have the opportunity to take 105 thousand rubles at the end of the year at an interest rate of 5 percent. Or we can choose another way of bonus when we are paid 50 thousand rubles every six months at the same interest rate.Compare these two payments. To do this, we calculate what the current value for each of these payments will be. Using the formula to find the current value, we need to discount 105 thousand at a rate of five percent (in this case, T = 1). We get 100 thousand.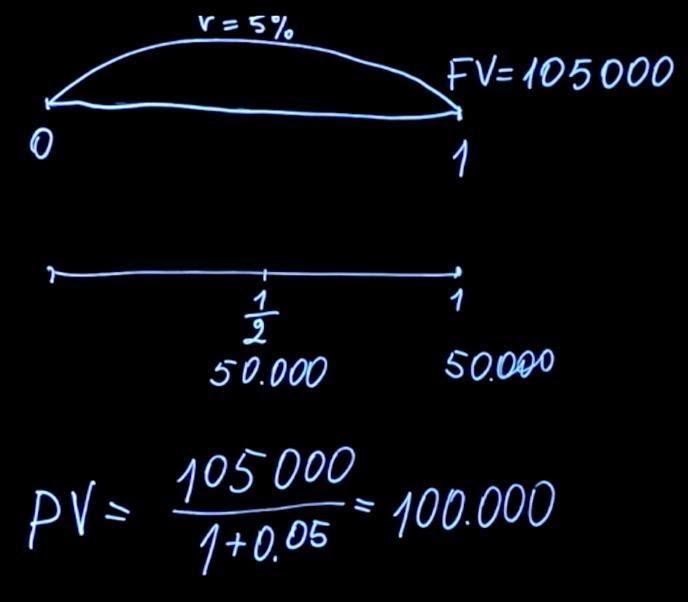
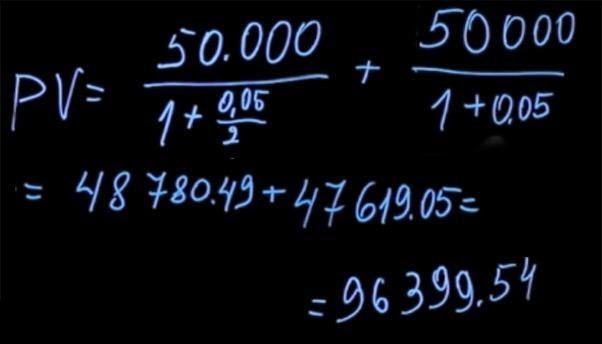
It’s more profitable to get a premium of 105 thousand rubles by waiting longer.
This principle works when assessing various life situations.For example, when you are offered to buy a car by installments or pay the full amount now with some kind of discount. You need to take the future amount that you pay, bring it to the current value, and then compare the payments that occur at the same time.
In this case, the comparison will be correct.# 3 Forward interest rates
Suppose we agree on an interest rate. At this interest rate, in a year I will borrow money from you, which I will repay in two years, plus interest. What should be the interest rate in order to be fair? We will describe this example in more detail.We are now at time zero. In a year, I will xtake money from you at a rate and return it to you in two years. How to calculate a bid x? We have several options. You can now put money at a rate of r1 per year, and then reinvest it at a rate x.Or put money right away at a rate of r2 for two years.There is a No-Arbitrage Condition in the financial market . It says that if at the end of the term we receive the same payments, then for instruments with the same risk, the initial amount should also be the same. Let's sign it too. The future value of the first investment option FV1 will be equal to the current value multiplied by the sum of units and rT1 (we assume that we have a simple interest calculation).The moment of time T1 is equal to one year. Next, we will have reinvestment of the amount, and we will put on a period of time from T2 - T1 , multiplied by our interest rate x. T2 - This is a point in time, in our case, two years.Or the future value of FV2 will equal the current value PVmultiplied by one plus r2 times T2 . According to the condition of no arbitration, FV1 must equal FV2 .From this we get the following:The formula is quite cumbersome. Let's calculate an example using this formula, and then think about what we can do to make it look simpler.Let our interest rates be r1 = 4%; r2 = 6%. In this case, we have the following:x=(1+0,06*2)/(1+0,04*1)-1 = 1,077-1 = 0,077 = 7,7%
It would seem strange that the rate for two years is equal to six percent, for a year it is equal to four percent, and from a year to two we get a rate of more than seven percent. This is explained as follows. Since in the first year we have an annual rate lower than two years, in the next year it should be higher than both of these rates. This is necessary in order to compensate for the lack of interest in the first year, and after reinvestment one could get the same amount as when investing for two years at a higher rate. This rate is called the forward interest rate.To make your life easier, let's simplify this formula. If we use the continuous interest calculation formula ( FV=PVerT ), then we can rewrite the condition for the absence of arbitration as follows:PVer 2 T 2 = PVer 1 T 1 e (T 2 -T 1 ) xIf we take the logarithm from both sides of our equality and reduce the constants, we get:r2 T2 = r1 T1 +(T2 -T1)xNext, it is easy to find x:x=(r2 T2 - r1 T1 )/(T2 -T1)Agree, such a formula for future interest rates is much easier and more convenient to use.You can ask a question - why such a strange product and who uses it?Imagine a situation where you or your company will definitely receive funds in a year. Now you would like to protect yourself from the risk of changes in interest rates. You understand that in a year the interest rate may increase and become more profitable, but also you understand that it can decrease. And you are quite comfortable with the forward interest rate operating in the market. Then you can conclude a contract, indicating in it that for the money that will be received in the future in a year, you conclude a contract at a given rate. The rate is fixed, and you no longer worry about how changes in interest rates in the market will occur.Please note that the forward interest rate is by no means a prediction of the future price. This absolutely does not mean that interest rates will be equal to 7.7% in a year, when we find ourselves at point T 1 . They can take on any value, and that’s why. At the moment when we calculate the forward interest rate from the rates in force in the market, we can say that this rate is the expectation of the market with respect to future prices. But by the time we move into the future, new events are happening, new information is being added, and the market is somehow changing. Therefore, interest rates in a year will not coincide with the forward rates calculated for the year now.Other articles in this series :- Bonds from A to Z. Likbez for a geek, Part 2 (will be available soon)