previous chapters

Final Debugging Algorithms

44. Test for optimization verification (The Optimization Verification test)

Suppose you are developing a speech recognition system. The system receives the input voice recording A and calculates a certain value A (S) , estimating the plausibility that this sound clip corresponds proposal S . For example, you can try to estimate the value of A (the S) = P (the S | A) , the probability that the correct output transcription will offer S, provided that the input sound was A .

Whatever method of estimating the quantity A (S) you choose, the task is to find the English sentence S at which this quantity will be maximum:

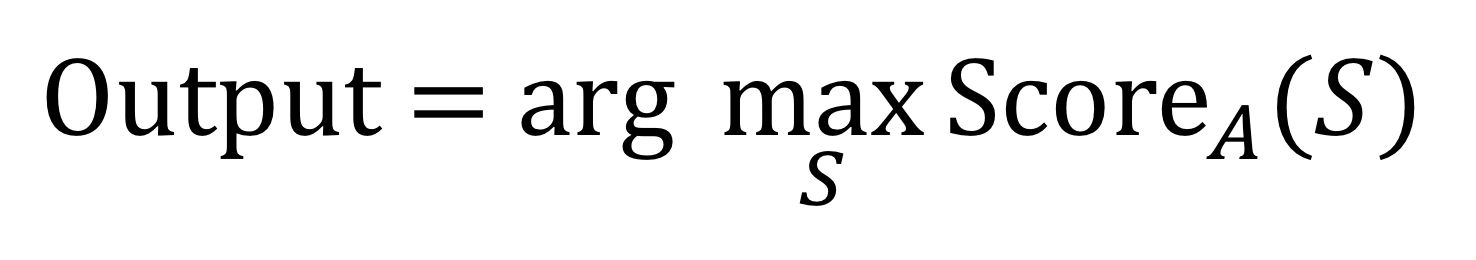
How to approach the calculation of "arg max" in this formula? Let's say 50,000 words in English, of which you can make

N — , , .

, , S, () A(S). « », K . ( , « »). , S, A(S).

, A -, « ». : « ».
:

1. . ( ) S, A(S).
2. ( ). A(S) = P(S|A) . , A(S) « » .

, - . . , A(S).

, ; A(S). , , .
?

(« »), S_out. (« »), S*. , , (The Optimization Verification test): Score_A(S*) Score_A(S_out), Score_A(S*) Score_A(S_out).

1: Score_A(S*) > Score_A(S_out)

S*, , S_out. , S_out, S*. , S, A(S) . (The Optimization Verification test) , , . , « » (beam search).

2: Score_A(S*) ≤ Score_A(S_out).

Score_A(.): S* S_out. (The Optimization Verification test) . , , Score_A(S) S.

. (The Optimization Verification test) , . , Score_A(S*) > Score_A(S_out). , , , . , Score_A(S*) ≤ Score_A(S_out) Score_A(.).

, , 95% Score_A(.), 5% - . , , ~ 5% . , Score_A(.).

45. (The Optimization Verification test).

(the Optimization Verification test) , , x , , x(y), , y x , arg max_yScore_x(y), , . x=A, y=S.

, y* — «» , y_out. Score_x(y*) > Score_x(y_out). , . , . , Score_x(y).

. , . C Score_C(E) E. , Score_C(E) = P(E|C), E, , C.

, , .

, E_out E*. , Score_C(E*) > Score_C(E_out). , Score_C(.) E* E_out; , . , Score_C(.).

« » : (approximate scoring function) Score_x(.), (approximate maximization algorithm). , (The Optimization Verification test) .

46.

, , . , , .

«». , . -. , , .

« » R(.), T. , T , R(T) = -1000 — «» . T, , R(T) , , . R(.), , T. , , , . — .

, R(T) , , , max_TR(T). .
, R(.) , . , , - — .

— , , , , max_TR(T) , , ?
(Optimization Verification test), T_human, , -, T_out . , T_human T_out. : , R(T_human) > R(T_out)?

1: , R(.) , T_human T_out. , , T_out, . , .

2: : R(T_human) ≤ R(T_out). , R(.) T_human , T_out, , T_human . R(.), .

«» Score_x(.) . x, Score(.). Score(T)=R(T), (optimization algorithm) , , T.

One of the differences between this and earlier examples is that the quality of the algorithm is not compared with the “optimal” result, but with the human trajectory T _human . We assumed that T _human is good enough, even if not optimal. In general, as long as you have some result y * (in this example, T _human ) that exceeds the quality of the system - even if it is not “optimal,” the Optimization Verification test will indicate that more promising: to improve the optimization algorithm or evaluation function.

continuation