Python COVID-19 pandemic simulation

Introduction

. . . , , . ? ? , . : , , , . , , . , , , , . Johns Hopkins University.

COVID-19 — , SARS-CoV-2 (2019-nCoV). — , /, .

• C
• C
• ()

, .

, , .

: |

, : , , , , , ( , ), . , , , , . , . , 2.4. , , , , — . , ( 15% ), , , ; .

, , , . . :

1. ,
2. .

:

1. , .
2. , ( ). , .
3. , , . .
4. - ( ) , .

— , - . COVID-19 1 14 .

. — . . , 0.35 ( , 2.4 , 1 14) 0.135 . , . .

Python

: . , , (Total cases), (New cases) (Infected), , ( - , ).

import numpy as np
import matplotlib.pyplot as plt

COUNTRY = "Italy"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 74
INCUBATION_PERIOD = 15

#   
np.random.seed(0)

#         . 
#     :     . 
#      ,   , , 
#            - .
def get_coef(day):
    return COEF_BASE if day < DAY_QUARANTINE else COEF_QUARANTINE

if __name__ == "__main__":
    #  
    days = np.arange(1, DAYS_OF_SIMULATION)

    #  
    infected = np.random.randint(1, INCUBATION_PERIOD, 1)

    infected_lst = []  #      ,      
    new_cases_lst = []
    new_cases_total_lst = []

    #    
    for day in days:
        #   
        coef = get_coef(day)

    #      
        new_cases_idx = np.argwhere(infected == day).flatten()

        #        
        new_cases_count = new_cases_idx.size

        #       ,  
        infected = np.delete(infected, new_cases_idx)

        #             
        new_infected_count = np.random.poisson(coef, infected.size).sum()
        new_infected = np.random.randint(1, INCUBATION_PERIOD, new_infected_count) + day
        infected = np.concatenate((infected, new_infected))

        #  
        infected_lst.append(infected.size)
        new_cases_lst.append(new_cases_count)
        new_cases_total_lst.append(sum(new_cases_lst))

        print(day, infected.size)

    plt.figure(figsize=(16, 8))

    #    
    plt.subplot(311)
    plt.title(f"COVID-19 pandemic in {COUNTRY}")
    plt.plot(days, new_cases_total_lst)
    plt.grid(True)
    plt.legend(["Total cases"], loc='upper left')

    #     
    plt.subplot(312)
    plt.bar(days, new_cases_lst, alpha=0.7, color='y')
    plt.grid(True)
    plt.legend(["New cases"], loc='upper left')

    #    
    plt.subplot(313)
    plt.plot(days, infected_lst, color='r')
    plt.grid(True)
    plt.legend(["Infected"], loc='upper left')

    plt.show()

.

DAYS_OF_SIMULATION -    ,
COEF_BASE -       ,
COEF_QUARANTINE -       ,
DAY_QUARANTINE -        ,
INCUBATION_PERIOD -       ( ).

, , .

, :

COUNTRY = "Italy"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 74
INCUBATION_PERIOD = 15

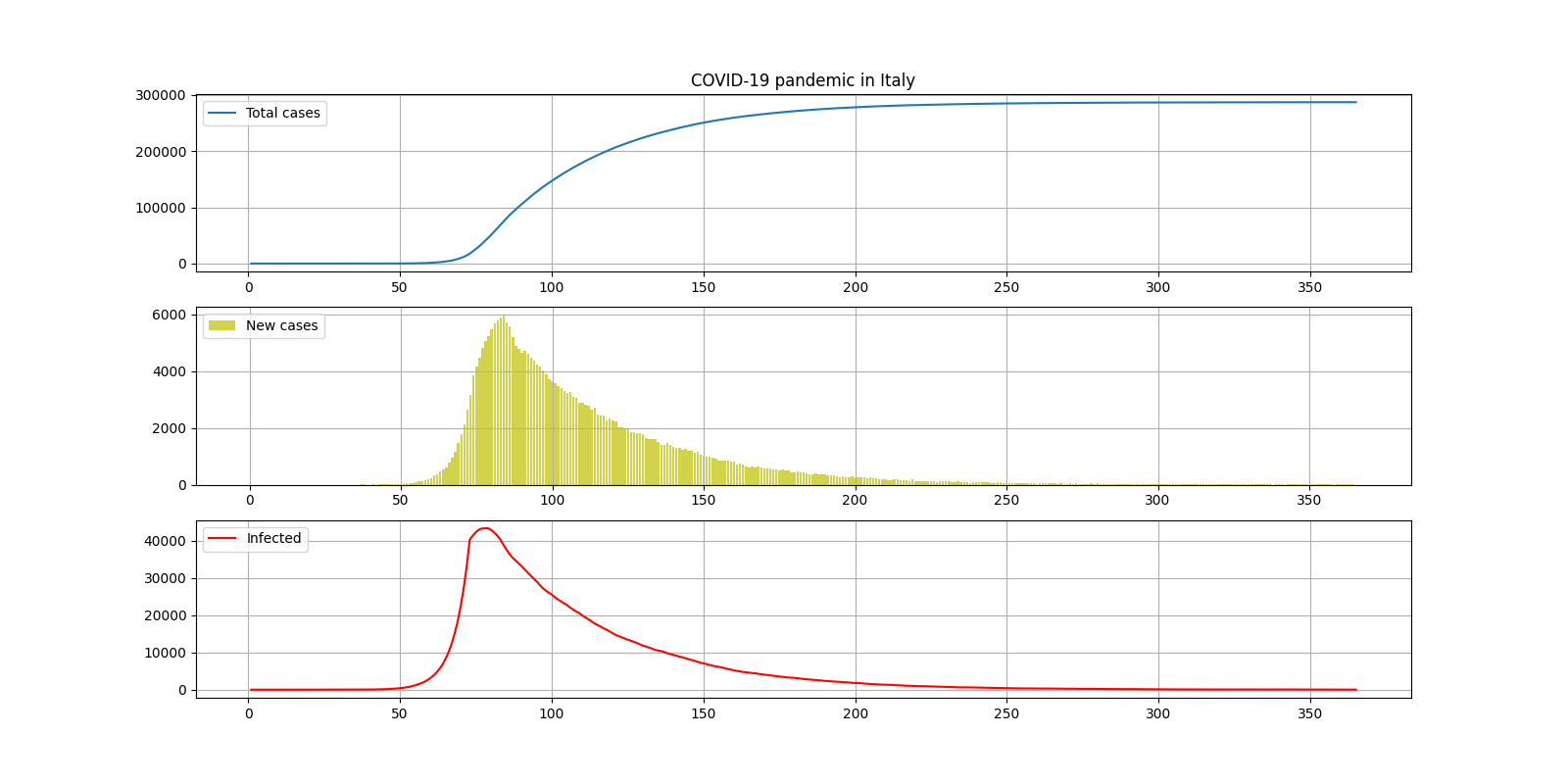
. - , ( 74- ), - , , 14 . , 300000, 250- , 180 ( , , 6 ). , 40000.

:
— 300000
— 6
— 40000

, , :

COUNTRY = "USA"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 83
INCUBATION_PERIOD = 15

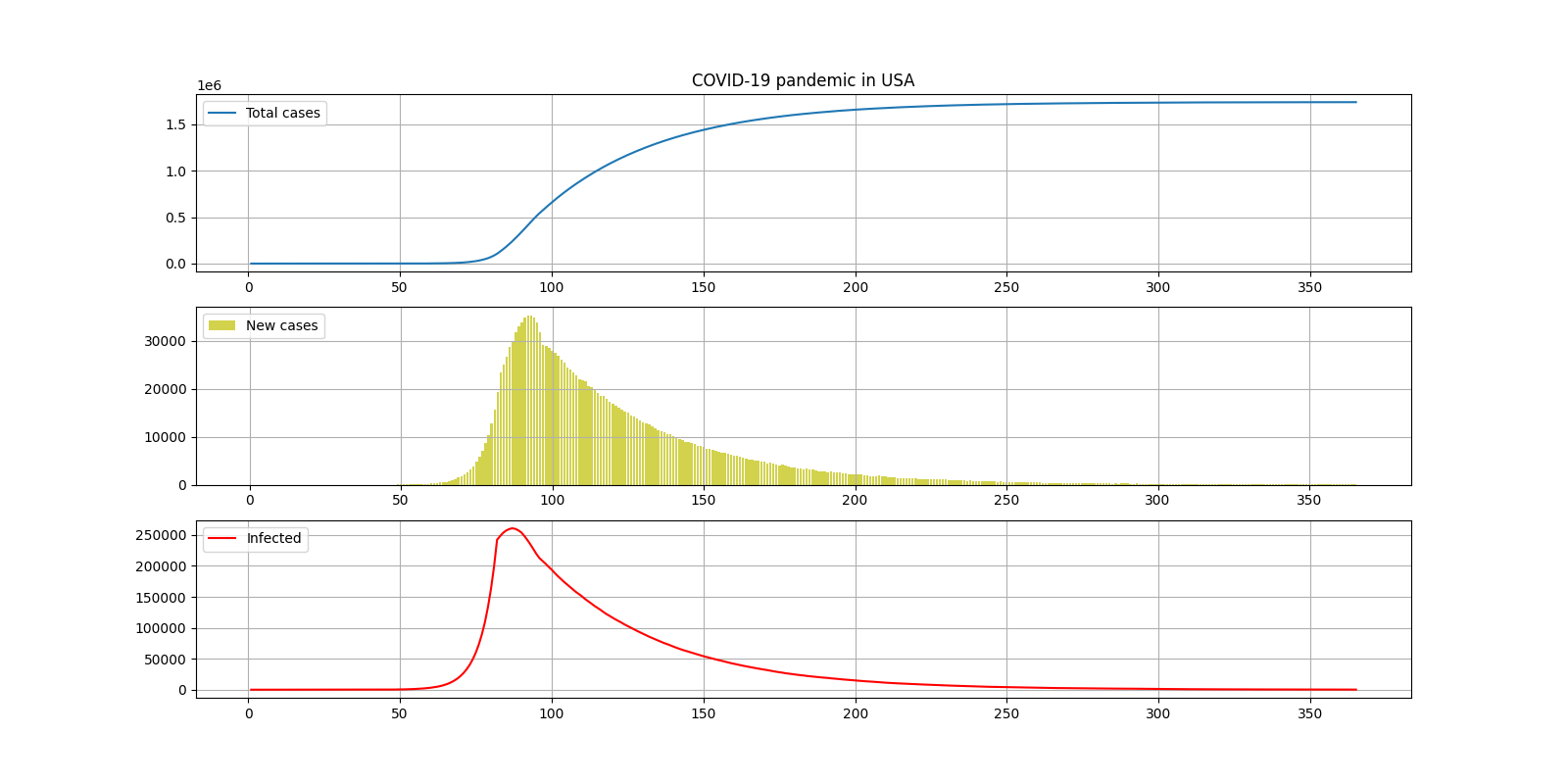
. , , ( DAY_QUARANTINE - ), , COEF_QUARANTINE . .

:
— 1700000
— 6
— 250000

— , . , , . "" . :

1. — .
2. 1 — .
3. 2 — .

.

I.

COUNTRY = "Russia"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 73
INCUBATION_PERIOD = 15

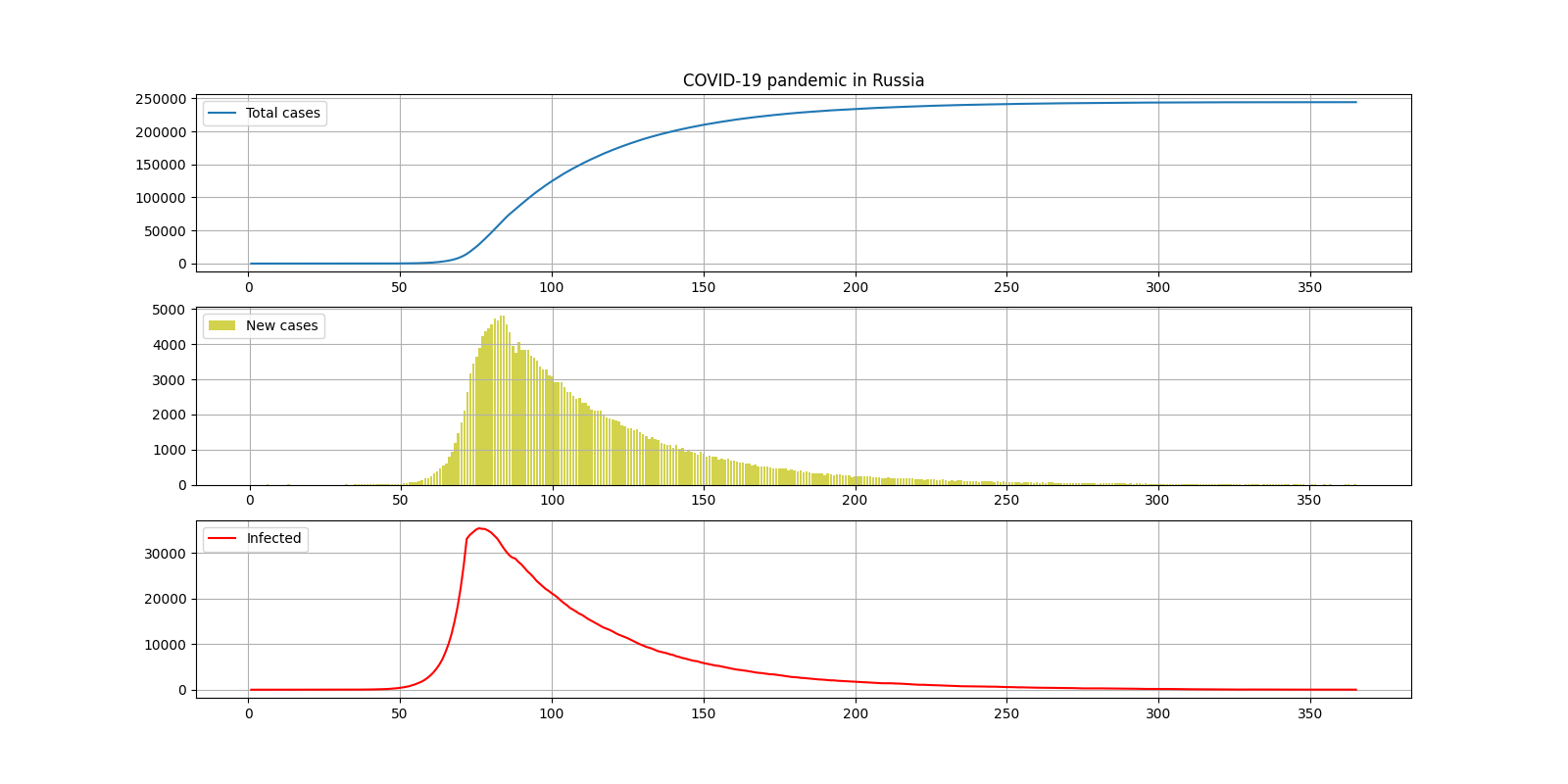
— 250000
— 6
— 35000

II. 1

COUNTRY = "Russia"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 80
INCUBATION_PERIOD = 15

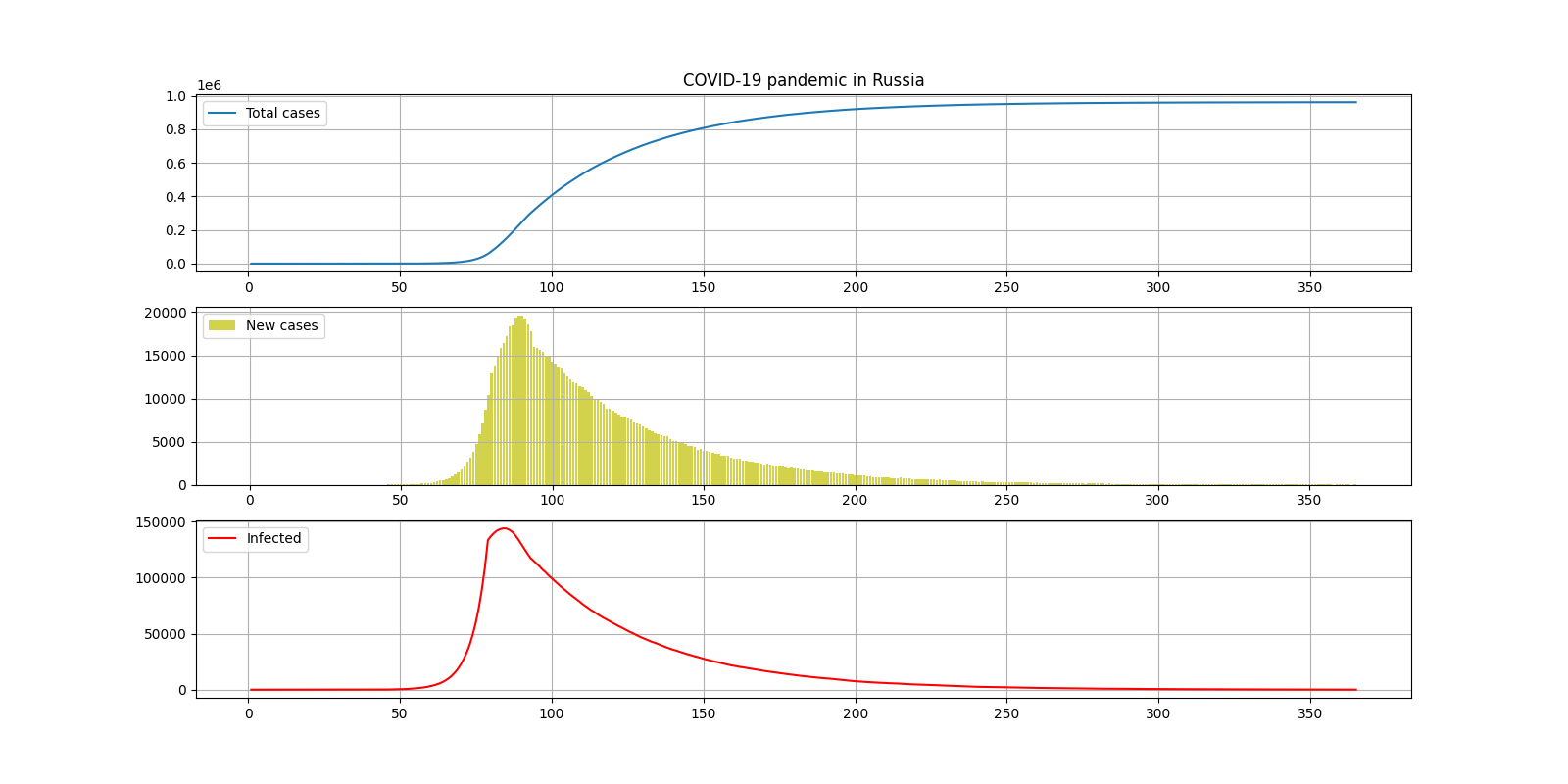
— 950000
— 7
— 140000

III. 2

COUNTRY = "Russia"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 87
INCUBATION_PERIOD = 15

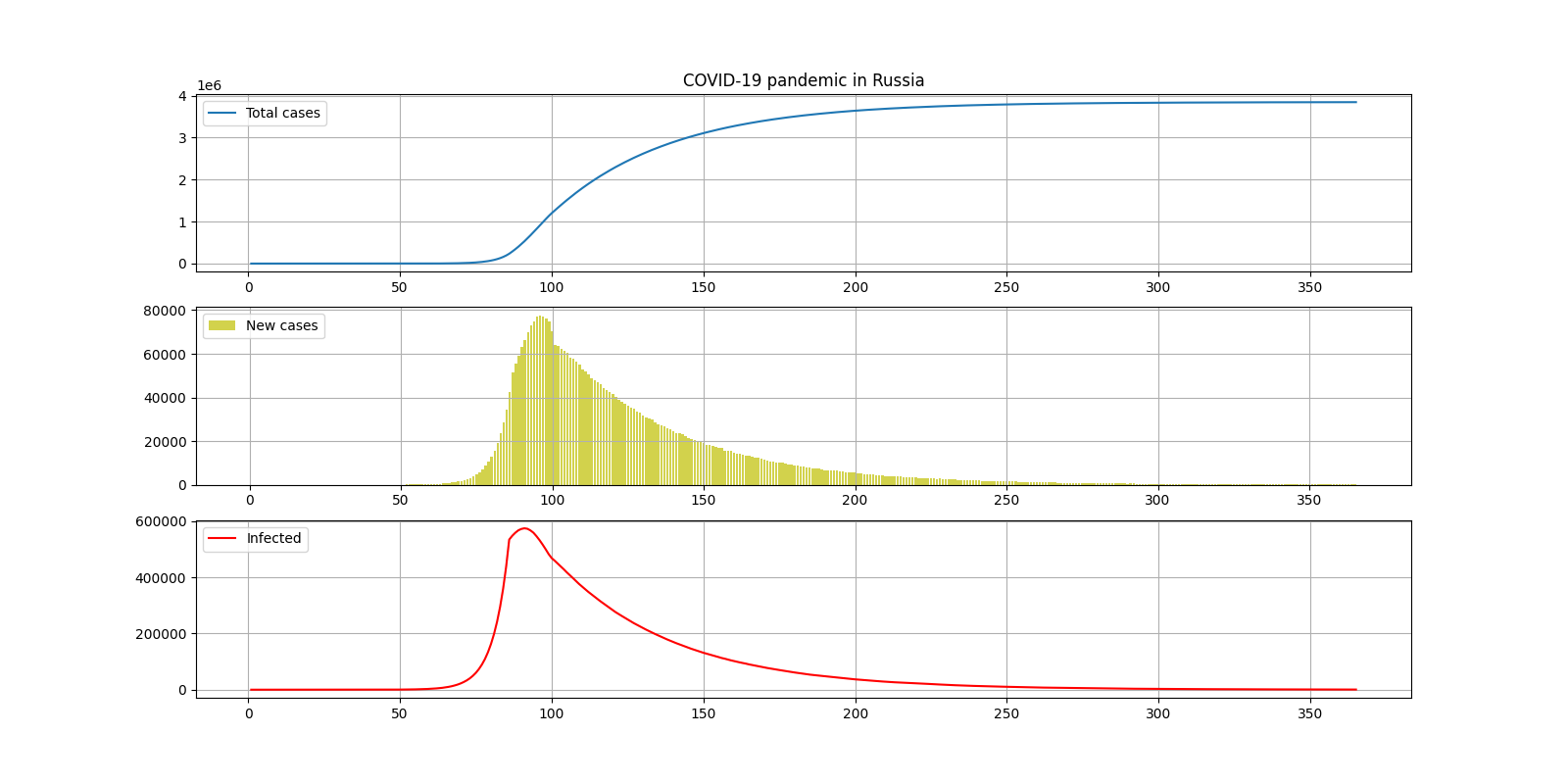
— 4000000
— 8
— 550000

, , -, DAY_QUARANTINE, COEF_QUARANTINE, ( , ). - :

1. , ;
2. ;
3. .

, , . , . , . :

1. , , ,
2. ,
3. ( , ),
4. ,
5. ,
6. … .

I suggest readers to play around with the script, try to simulate the process for other countries, unsubscribe in the comments. It’s also interesting to complicate the simulation by adding more unaccounted factors.