In anticipation of the start of the course "Algorithms for Developers" have prepared for you a translation of another useful material.
Huffman coding is a data compression algorithm that formulates the basic idea of file compression. In this article, we will talk about fixed and variable length coding, uniquely decoded codes, prefix rules, and the construction of a Huffman tree.We know that each character is stored as a sequence of 0 and 1 and takes 8 bits. This is called fixed-length encoding because each character uses the same fixed number of bits to store.Let's say the text is given. How can we reduce the amount of space required to store one character?The basic idea is variable length coding. We can use the fact that some characters in the text are more common than others ( see here ) to develop an algorithm that will represent the same sequence of characters with fewer bits. When coding a variable length, we assign a variable number of bits to the characters depending on the frequency of their appearance in this text. Ultimately, some characters may take up just 1 bit, and others 2 bits, 3 or more. The problem with variable length encoding is only the subsequent decoding of the sequence.How, knowing the sequence of bits, to decode it uniquely?Consider the string “aabacdab” . It has 8 characters, and when encoding a fixed length, 64 bits will be needed to store it. Note that the frequency of the characters “a”, “b”, “c” and “d” is 4, 2, 1, 1, respectively. Let's try to imagine “aabacdab” with fewer bits, using the fact that “a” is more common than “b” and “b” is more common than “c” and “d” . To begin with, we encode “a” using one bit equal to 0, “b” we assign a two-bit code 11, and using three bits 100 and 011 we encode “c” and"D" .As a result, we will succeed:Thus, we encode the string “aabacdab” as 00110100011011 (0 | 0 | 11 | 0 | 100 | 011 | 0 | 11) using the codes presented above. However, the main problem will be decoding. When we try to decode the line 00110100011011 , we get an ambiguous result, since it can be represented as:0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
...etc.To avoid this ambiguity, we must ensure that our encoding satisfies a concept such as a prefix rule , which in turn implies that codes can be decoded in just one unique way. A prefix rule ensures that no code is a prefix of another. By code, we mean bits used to represent a particular character. In the above example, 0 is the prefix 011 , which violates the prefix rule. So, if our codes satisfy the prefix rule, then we can uniquely decode (and vice versa).Let's review the example above. This time we will assign the characters “a”, “b”, “c” and “d” Codes that satisfy the prefix rule.Using this encoding, the string “aabacdab” will be encoded as 00100100011010 (0 | 0 | 10 | 0 | 100 | 011 | 0 | 10) . But 00100100011010 we can uniquely decode and return to our original line “aabacdab” .Huffman coding
Now that we’ve figured out variable-length coding and a prefix rule, let's talk about Huffman coding.The method is based on the creation of binary trees. In it, a node can be either finite or internal. Initially, all nodes are considered leaves (leafs), which represent the symbol itself and its weight (that is, the frequency of occurrence). Internal nodes contain the weight of the character and refer to two descendant nodes. By general agreement, bit “0” represents a follow on the left branch, and “1” represents on the right. In a complete tree there are N leaves and N-1 internal nodes. It is recommended that when building a Huffman tree, unused characters be discarded to obtain codes of optimal length.We will use the priority queue to build the Huffman tree, where the node with the lowest frequency will be given the highest priority. The construction steps are described below:- Create a leaf node for each character and add them to the priority queue.
- While in line for more than one sheet, do the following:
- Remove the two nodes with the highest priority (with the lowest frequency) from the queue;
- Create a new internal node where these two nodes will be heirs, and the frequency of occurrence will be equal to the sum of the frequencies of these two nodes.
- Add a new node to the priority queue.
- The only remaining node will be the root, this will finish the tree construction.
Imagine that we have some text that consists only of the characters “a,” “b,” “c,” “d,” and “e,” and the frequencies of their appearance are 15, 7, 6, 6, and 5, respectively. Below are illustrations that reflect the steps of the algorithm.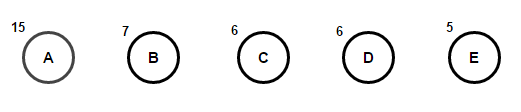

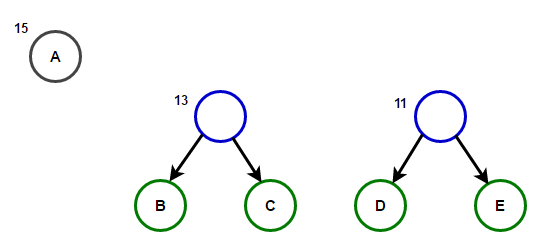
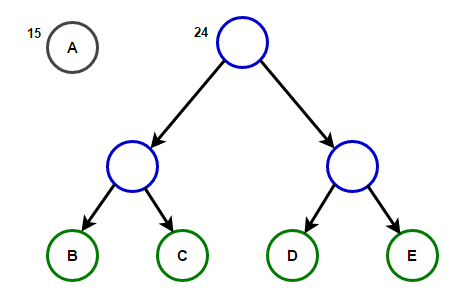
 The path from the root to any end node will store the optimal prefix code (also known as the Huffman code) corresponding to the character associated with that end node.
The path from the root to any end node will store the optimal prefix code (also known as the Huffman code) corresponding to the character associated with that end node. Huffman TreeBelow you will find the implementation of the Huffman compression algorithm in C ++ and Java:
Huffman TreeBelow you will find the implementation of the Huffman compression algorithm in C ++ and Java:#include <iostream>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
struct Node
{
char ch;
int freq;
Node *left, *right;
};
Node* getNode(char ch, int freq, Node* left, Node* right)
{
Node* node = new Node();
node->ch = ch;
node->freq = freq;
node->left = left;
node->right = right;
return node;
}
struct comp
{
bool operator()(Node* l, Node* r)
{
return l->freq > r->freq;
}
};
void encode(Node* root, string str,
unordered_map<char, string> &huffmanCode)
{
if (root == nullptr)
return;
if (!root->left && !root->right) {
huffmanCode[root->ch] = str;
}
encode(root->left, str + "0", huffmanCode);
encode(root->right, str + "1", huffmanCode);
}
void decode(Node* root, int &index, string str)
{
if (root == nullptr) {
return;
}
if (!root->left && !root->right)
{
cout << root->ch;
return;
}
index++;
if (str[index] =='0')
decode(root->left, index, str);
else
decode(root->right, index, str);
}
void buildHuffmanTree(string text)
{
unordered_map<char, int> freq;
for (char ch: text) {
freq[ch]++;
}
priority_queue<Node*, vector<Node*>, comp> pq;
for (auto pair: freq) {
pq.push(getNode(pair.first, pair.second, nullptr, nullptr));
}
while (pq.size() != 1)
{
Node *left = pq.top(); pq.pop();
Node *right = pq.top(); pq.pop();
int sum = left->freq + right->freq;
pq.push(getNode('\0', sum, left, right));
}
Node* root = pq.top();
unordered_map<char, string> huffmanCode;
encode(root, "", huffmanCode);
cout << "Huffman Codes are :\n" << '\n';
for (auto pair: huffmanCode) {
cout << pair.first << " " << pair.second << '\n';
}
cout << "\nOriginal string was :\n" << text << '\n';
string str = "";
for (char ch: text) {
str += huffmanCode[ch];
}
cout << "\nEncoded string is :\n" << str << '\n';
int index = -1;
cout << "\nDecoded string is: \n";
while (index < (int)str.size() - 2) {
decode(root, index, str);
}
}
int main()
{
string text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
return 0;
}
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class Node
{
char ch;
int freq;
Node left = null, right = null;
Node(char ch, int freq)
{
this.ch = ch;
this.freq = freq;
}
public Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
};
class Huffman
{
public static void encode(Node root, String str,
Map<Character, String> huffmanCode)
{
if (root == null)
return;
if (root.left == null && root.right == null) {
huffmanCode.put(root.ch, str);
}
encode(root.left, str + "0", huffmanCode);
encode(root.right, str + "1", huffmanCode);
}
public static int decode(Node root, int index, StringBuilder sb)
{
if (root == null)
return index;
if (root.left == null && root.right == null)
{
System.out.print(root.ch);
return index;
}
index++;
if (sb.charAt(index) == '0')
index = decode(root.left, index, sb);
else
index = decode(root.right, index, sb);
return index;
}
public static void buildHuffmanTree(String text)
{
Map<Character, Integer> freq = new HashMap<>();
for (int i = 0 ; i < text.length(); i++) {
if (!freq.containsKey(text.charAt(i))) {
freq.put(text.charAt(i), 0);
}
freq.put(text.charAt(i), freq.get(text.charAt(i)) + 1);
}
PriorityQueue<Node> pq = new PriorityQueue<>(
(l, r) -> l.freq - r.freq);
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
pq.add(new Node(entry.getKey(), entry.getValue()));
}
while (pq.size() != 1)
{
Node left = pq.poll();
Node right = pq.poll();
int sum = left.freq + right.freq;
pq.add(new Node('\0', sum, left, right));
}
Node root = pq.peek();
Map<Character, String> huffmanCode = new HashMap<>();
encode(root, "", huffmanCode);
System.out.println("Huffman Codes are :\n");
for (Map.Entry<Character, String> entry : huffmanCode.entrySet()) {
System.out.println(entry.getKey() + " " + entry.getValue());
}
System.out.println("\nOriginal string was :\n" + text);
StringBuilder sb = new StringBuilder();
for (int i = 0 ; i < text.length(); i++) {
sb.append(huffmanCode.get(text.charAt(i)));
}
System.out.println("\nEncoded string is :\n" + sb);
int index = -1;
System.out.println("\nDecoded string is: \n");
while (index < sb.length() - 2) {
index = decode(root, index, sb);
}
}
public static void main(String[] args)
{
String text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
}
}
Note: the memory used by the input string is 47 * 8 = 376 bits, and the encoded string takes only 194 bits, i.e. data is compressed by about 48%. In the C ++ program above, we use the string class to store the encoded string to make the program readable.Since effective data structures of the priority queue require O (log (N)) time to be inserted, and in a complete binary tree with N leaves there are 2N-1 nodes, and the Huffman tree is a complete binary tree, the algorithm works for O (Nlog (N )) time, where N is the number of characters.Sources:
en.wikipedia.org/wiki/Huffman_codingen.wikipedia.org/wiki/Variable-length_codewww.youtube.com/watch?v=5wRPin4oxCo
.