Since I encountered significant difficulties in finding an explanation of the back propagation mechanism of the error that I would like, I decided to write my own post about the back propagation of the error using the Word2Vec algorithm. My goal is to explain the essence of the algorithm using a simple but non-trivial neural network. In addition, word2vec has become so popular in the NLP community that it will be useful to focus on it.
This post is connected with another, more practical post that I recommend reading, it discusses the direct implementation of word2vec in python. In this post, we will focus mainly on the theoretical part.
Let's start with the things that are necessary for a true understanding of back propagation. In addition to concepts from machine learning, such as the loss function and gradient descent, two more components from mathematics come in handy:
If you are familiar with these concepts, then further considerations will be simple. If you have not mastered them yet, you can still understand the basics of backpropagation.
First, I want to define the concept of back propagation, if the meaning is not clear enough, it will be disclosed in more detail in the following paragraphs.
1. What is a backpropagation algorithm?
Within the framework of a neural network, the only parameters involved in training the network, that is, to minimize the loss function, are weights (here I mean weights in the broad sense, including displacements). Weights change at each iteration until we get to the minimum of the loss function.
, — , , .
, , .
, , , , w1 w2.

1. .
, w1 w2 .
, . , ∂L/∂w1 ∂L/∂w2, , . η, .
2. Word2Vec
word2vec, , , . , word2vec, NLP.
, word2vec [N, 3], N - , . , , '', , ( ), , ''. , word2vec .
word2vec : (CBOW) (skip-gram). , CBOW, , skip-gram.
. , woed2vec .
3. CBOW
CBOW . , :
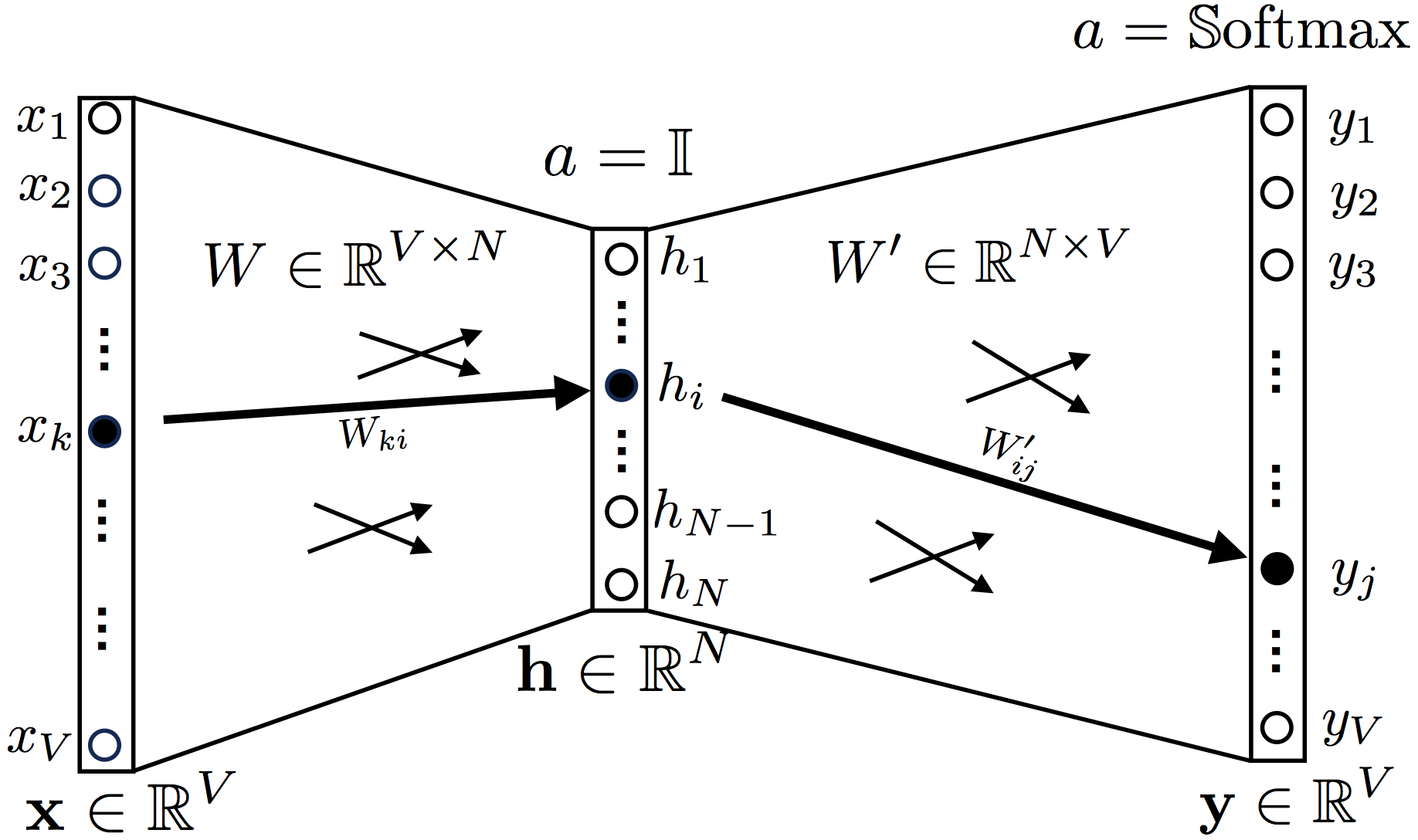
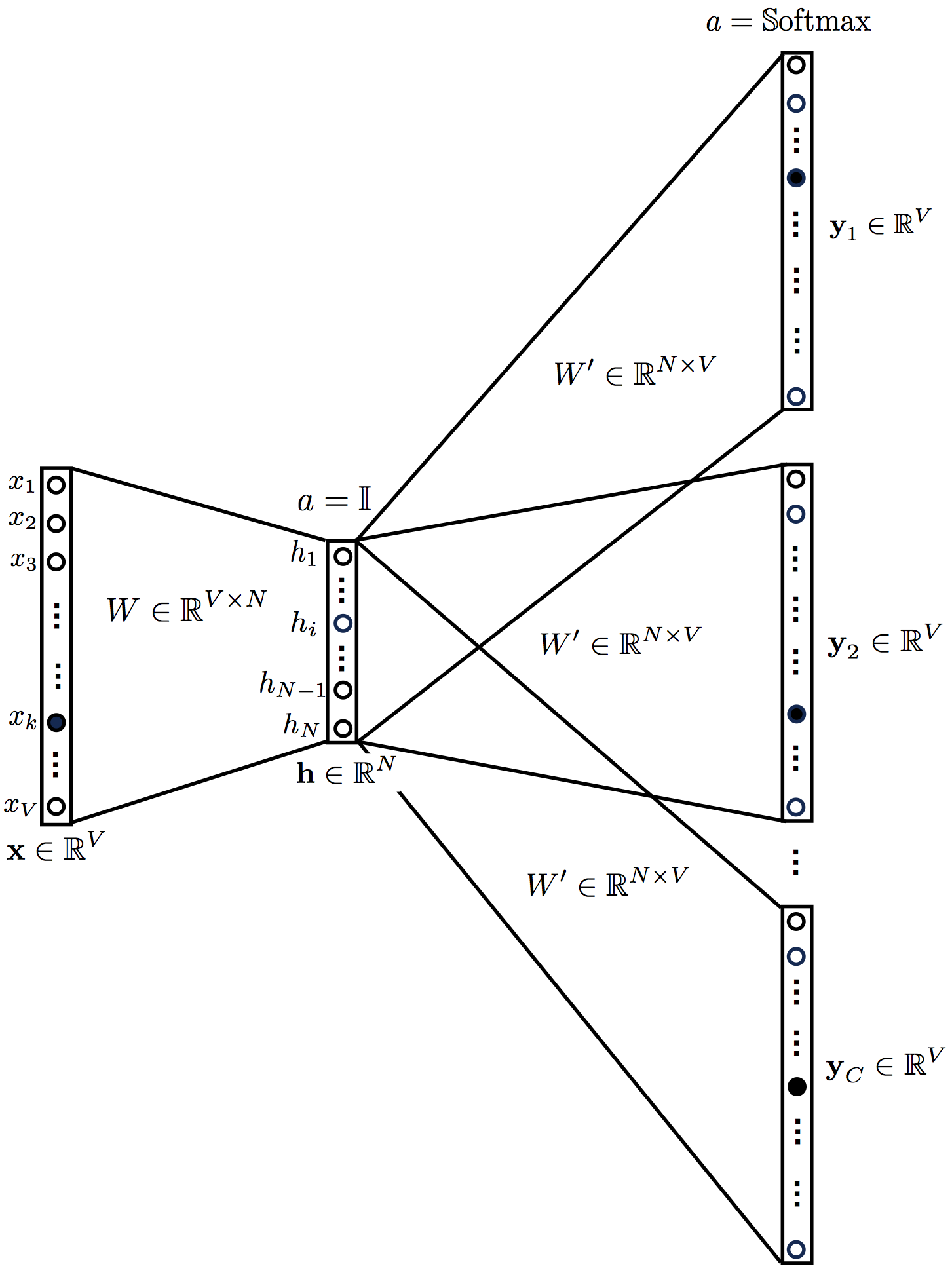
2. Continuous Bag-of-Words
, ,
a = 1 (identity function, , ).
Softmax.
one hot encoding , , , , , 1.
: ['', '', '', '', '', '']
OneHot('') = [0, 0, 0, 1, 0, 0]
OneHot(['', '']) = [1, 0, 0, 1, 0, 0]
OneHot(['', '', '']) = [1, 0, 0, 0, 1, 1]
, W V×N, W′ N×V, V — , N — ( , word2vec)
y t, , , , , .
, .
, word2vec :
"I like playing football"
CBOW (2) .
, 4 , V=4, , N=2, :
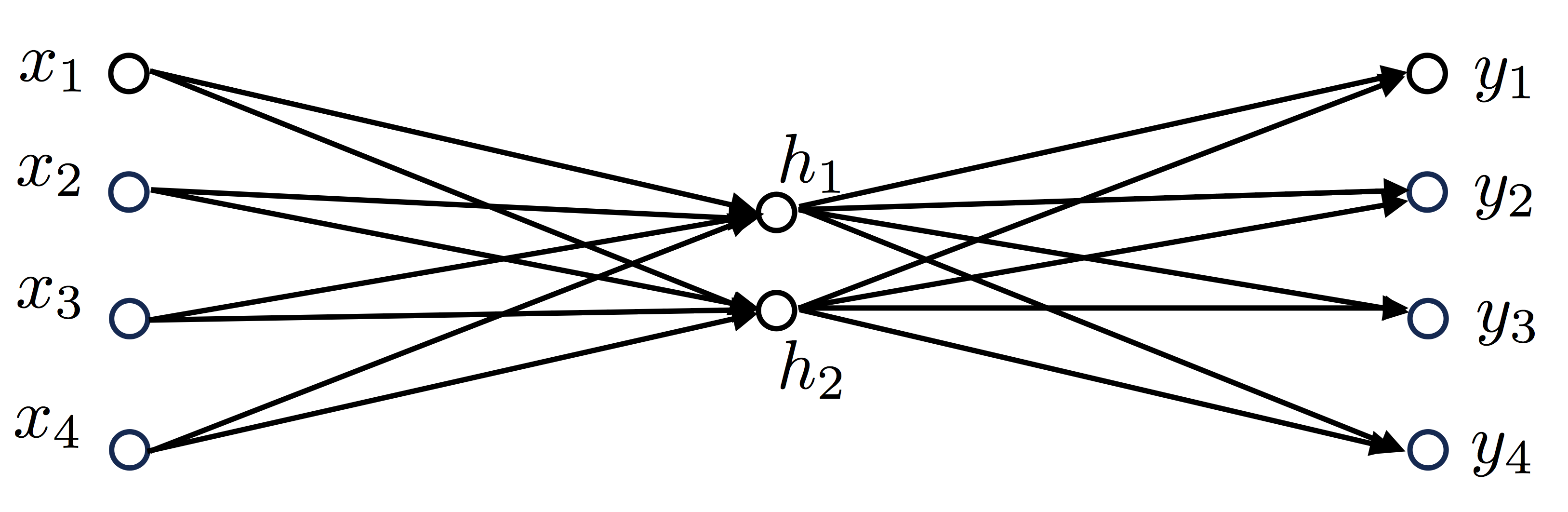
:
Vocabulary=[“I”,“like”,“playing”,“football”]
'' '' , . :

:
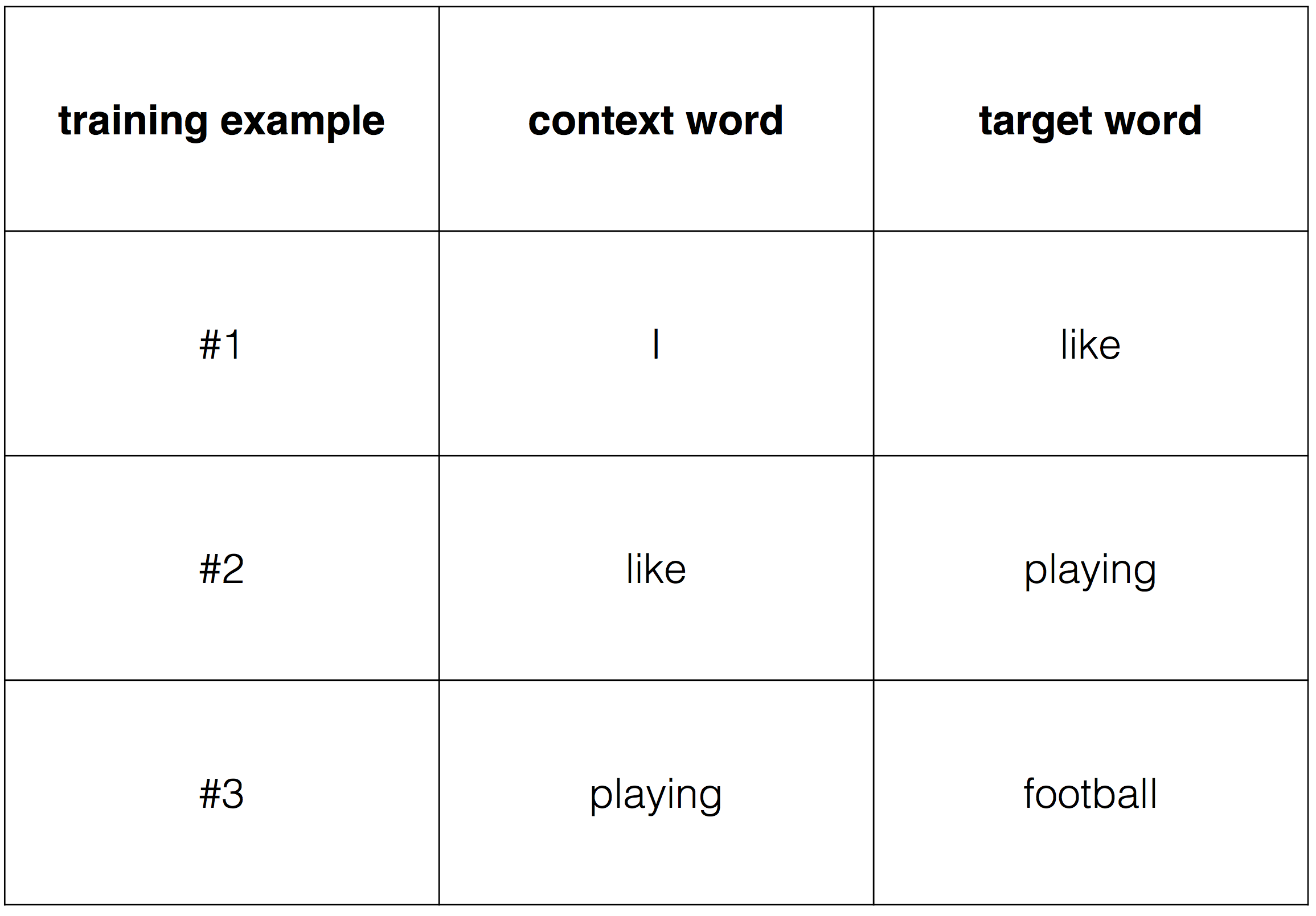
, one-hot encoding.
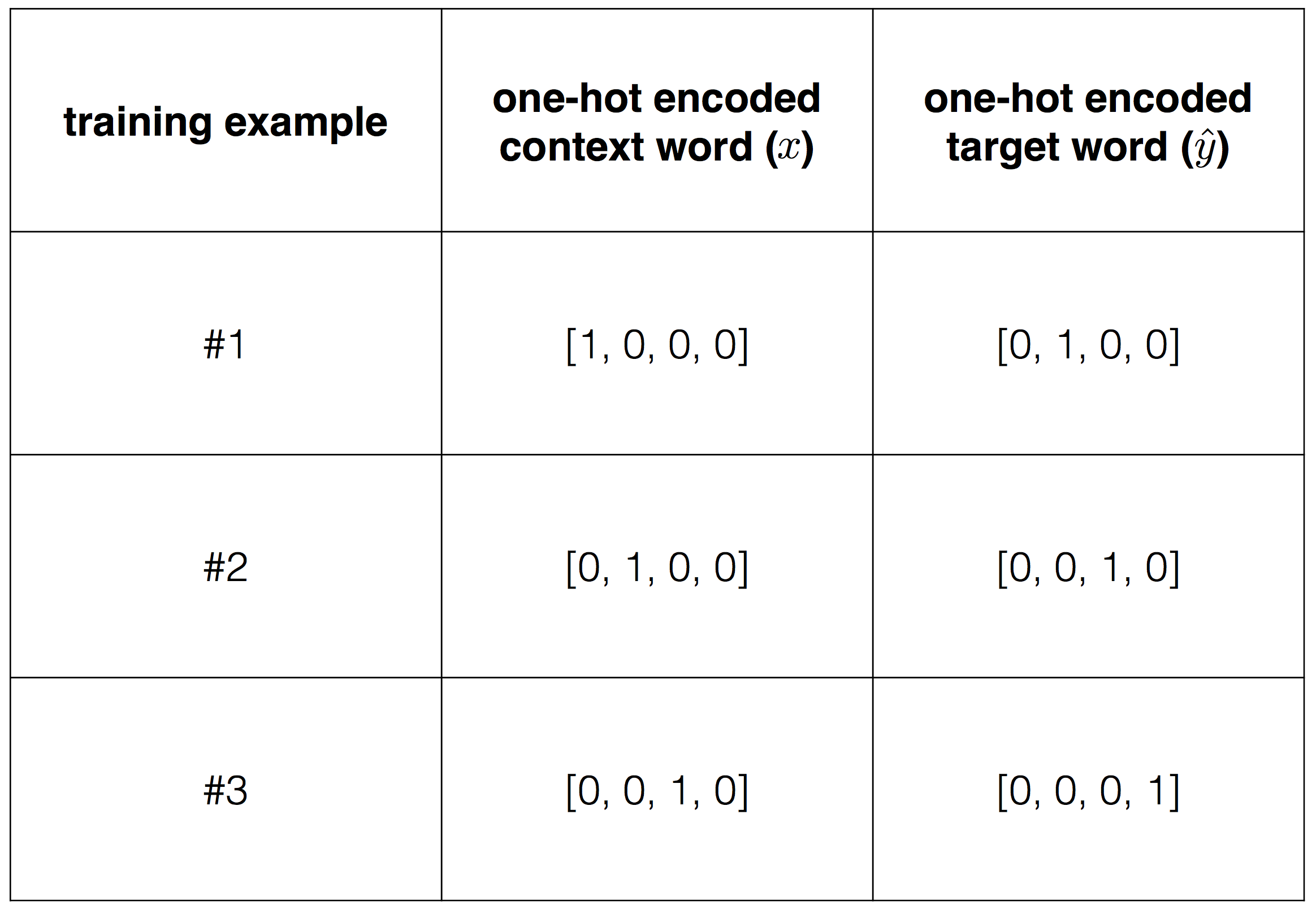
, , , . , , .
3.1 (Loss function)
1, , x:
h=WTxu=W′Th=W′TWTxy= Softmax(u)=Softmax(W′TWTx)
, h — , u — , y — .
, , , (wt, wc). , onehot encoding .
, onehot wt ( ).
softmax , :
, j* — .
. (1):
.
"I like play football", , "I" "like", , x=(1,0,0,0) — "I", ˆy=(0,1,0,0), "like".
word2vec, . W 4×2
W=(−1.381187280.548493730.39389902−1.1501331−1.169676280.360780220.06676289−0.14292845)
W′ 2×4
W′=(1.39420129−0.894417570.998696670.444470370.69671796−0.233643410.21975196−0.0022673)
"I like" :
h=WTx=(−1.381187280.54849373)
u=W′Th=(−1.543507651.10720623−1.25885456−0.61514042)
y=Softmax(u)=(0.052565670.74454790.069875590.13301083)
y,
L=−logP(“like”|“I”)=−logy3=−log(0.7445479)=0.2949781.
, (1):
L=−u2+log4∑i=1ui=−1.10720623+log[exp(−1.54350765)+exp(1.10720623)+exp(−1.25885456)+exp(−0.61514042)]=0.2949781.
, "like play", , .
3.2 CBOW
, , W W` . , .
. (1) W W`. ∂L/∂W ∂L/∂W′
, . (1) W W`, u=[u1, ...., uV],
:
, (2) (3) .
(2), Wij, W, i j , uj ( yj).
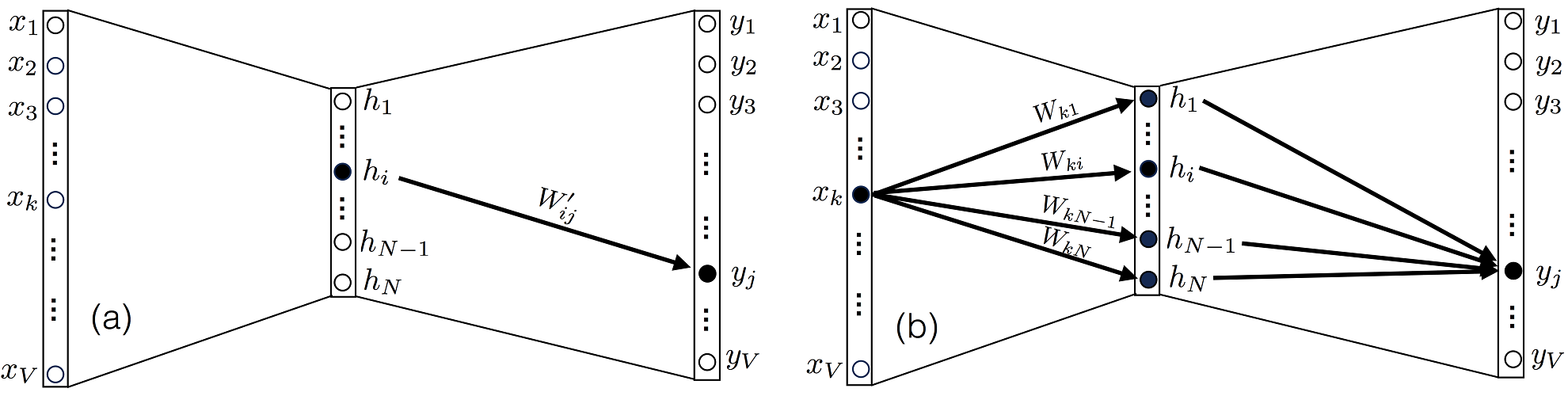
3. (a) yj hi W′ij W′. (b) , xk N Wk1…WkN W.
, ∂uk/∂W′ij, , k=j, 0.
(4):
∂L/∂uj, (5):
, δjj∗ — , , 1, , 0 .
(5) e N ( ), , , .
(4) (6):
(5) (6) (4) (7):
∂L/∂Wij, Xk, yj j W , 3(b). . ∂uk/∂Wij, uk u :
∂uk/∂Wij, l=i m=j, (8):
(5) (8) , (9):
. (7) (9) . (7)
⊗ .
(9) :
3.3
, (7) (9), , . . η>0, :
Wnew=Wold−η∂L∂WW′new=W′old−η∂L∂W′
3.4
. , . , . , . , , , .
4. CBOW
CBOW . . (4) . OneHot Encoded . word2vec. .

4. CBOW
CBOW CBOW .
h=1CWTC∑c=1x(c)=WT¯xu=W′Th=1CC∑c=1W′TWTx(c)=W′TWT¯xy= Softmax(u)=Softmax(W′TWT¯x)
, '' ¯x=∑Cc=1x(c)/C
, . :
, :
CBOW , , . W′ij
Wij:
:
(17) (18) .
(17) :
(18):
, CBOW .
⊗ .
5. Skip-gram
CBOW, , . :
5. Skip-gram .
skip-gram :
h=WTxuc=W′Th=W′TWTxc=1,…,Cyc= Softmax(u)=Softmax(W′TWTx)c=1,…,C
( uc) , y1=y2⋯=yC. :
L=−logP(wc,1,wc,2,…,wc,C|wo)=−logC∏c=1P(wc,i|wo)=−logC∏c=1exp(uc,j∗)∑Vj=1exp(uc,j)=−C∑c=1uc,j∗+C∑c=1logV∑j=1exp(uc,j)
skip-gram C×V
:
:
∂L/∂uc,j, :
CBOW :
Wij , :
, skip-gram :
(21):
(22):
6.
word2vec. . [2] ( softmax, negative sampling), . [1].
, word2vec.
The next step is to implement these equations in your favorite programming language. If you like Python, I already implemented these equations in my next post .
Hope to see you there!
Sitelinks
[1] X. Rong, word2vec Parameter Learning Explained , arXiv: 1411.2738 (2014).
[2] T. Mikolov, K. Chen, G. Corrado, J. Dean, Efficient Estimation of Word Representations in Vector Space , arXiv: 1301.3781 (2013).