The parameters and principles of operation of various systems can be connected by a selected attribute among themselves with various kinds of relationships. If, let’s say, we are interested in the effect of the price of a service on its demand, then this relationship can be described by a relationship of the type “influences”, “strongly influences”, “weakly influences”, etc. In this case, quite “discrete” objects for description may not be enough. For many applied problems of the theory of automata, pattern recognition, decision making, etc. it makes sense to generalize the concept of the relationship between objects to a fuzzy case. In this case, the model, quite possibly, will more adequately describe the system, allowing a qualitative analysis of systems without loss of threshold information, in connection with the emergence of new types of relationships: similarity, similarity, dissimilarity, ...
The concept of fuzzy relationships (connections, associations, relationships, relationships are synonyms), along with the concept of fuzzy sets, refers to the fundamental foundations of the whole theory of fuzzy sets. In addition to the fact that they themselves have applied value, on their basis a number of additional concepts are determined that are used to build fuzzy models of more complex systems.
Fuzzy relationship
 (sorry)
(sorry)Definition
As in the case of fuzzy sets (HMs), fuzzy relationships generalize the concept of the usual relationship we are familiar with in (naive) set theory. And many concepts introduced below for relations will be similar to the corresponding concepts for NM.
We introduce the concepts of fuzzy relationship and consider its properties.
Fuzzy 2-ary (binary) ratio on the universal set , . :
n- n- .
, - ( , ..). . . , n- .
.
- ;
- ;
- ;
- , — , — . ( , . , , , xD)
.
« » ( x>>y ). :

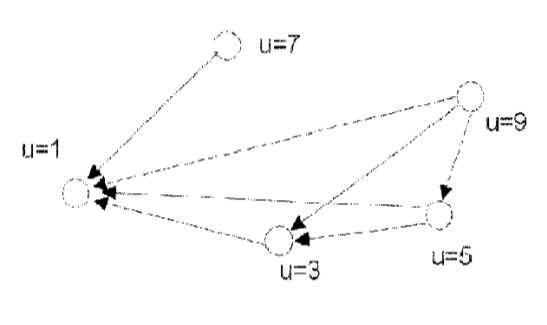
—
:
,
( ) :
:
:
, , — .
, :
, , 0.5 0.
, .
:
. The set of all fuzzy relations forms a distributive lattice in relation to the operations of union and intersection; and from the fulfillment of the identities of idempotency, commutativity, associativity, absorption and distributivity for the lattice the fulfillment of these identities for all relations follows.In logic based on the theory of ordinary sets, a statement like “the numbers x and y are very close or / and very different” should be reduced to “the numbers x and y are very close or very different”. However, in the theory of fuzzy sets, the first statement is quite logical; it expresses the fact that the connective “and” is interpreted for very small values of the membership function, when it is impossible to say about x and y that they are very close or that they are very different from each other. This example illustrates well the flexibility of utterances inherent in real logic.
: ; : .
, . - . , . - . , .
( ) . .
. , . (Max-*)-. , 3 .
- max-min ( ): . .
- min-max ( ): .
- max-• ( ): .
, . :
:
- ;
- ;
- .
. :
:;
: ;
: ;
flexx: ;
: ;
: ;
: ;
: .
… . .
2 NPC-, . , . NPC :
, , .
, , — .
, , :
« »
« »
« »
. : NPC ?
, :
def very(arr: List[set]):
return [(elem[0]**2, elem[1]) for elem in arr]
def no(arr: List[set]):
return [(1 - elem[0], elem[1]) for elem in arr]
def attitude(a: List[set], b: List[set], func = lambda x, y: min(x, y)):
return [[func(i[0], j[0]) for j in b] for i in a]
def attitude_unite(a: List[List], b: List[List]):
return [[max(a[i][j], b[i][j]) for j in range(len(a[i]))] for i in range(len(a))]
def composition(a: List[List], b: List[List]):
result = [[0 for j in range(len(b[0]))] for i in range(len(a))]
for x in range(len(a)):
for z in range(len(b[0])):
maximum = min(a[x][0], b[0][z])
for y in range(0, len(a[0])):
if maximum < min(a[x][y], b[y][z]):
maximum = min(a[x][y], b[y][z])
result[x][z] = maximum
return result
def index_plus(a: List[List]):
maximum = max([elem[1] for elem in a])
result = 0
for i in range(len(a)):
result += a[i][0] * (a[i][1] + maximum) / 2
return result
def ranking_index(a: List[List], b: List[List]):
return index_plus(a) - index_plus(b)
, — -. , , , index_plus ranking_index. . ( ; , ) :
— . . :
A = [(0.8, 3), (0.4, 15), (0.3, 30)]
B = [(0.1, 0.9), (0.5, 0.5), (0.8, 0.1)]
C = [(0.8, 0.9), (0.5, 0.5), (0.3, 0.2)]
— « ». 1 3 :
x = no(very(A))
x = [[elem[0] for elem in x]]
NPC K1R1. R1=A×B ∪ A¯×B¯:
AonB = attitude(A, B)
notAonnotB = attitude(no(A), no(B))
R1 = attitude_unite(AonB, notAonnotB)
y1, ( ) R1.
y1 = composition(x, R1)
print('y1 = ', y1)
:
notAonC = attitude(no(A), C)
AonnotC = attitude(A, no(C))
R2 = attitude_unite(notAonC, AonnotC)
y2 = composition(x, R2)
print('y2 = ', y2)
y1y2:
y1 = [(y1[0][i], B[i][1]) for i in range(len(y1[0]))]
y2 = [(y2[0][i], C[i][1]) for i in range(len(y2[0]))]
NPC:
print('index = ', ranking_index(y1, y2))
A small negative value indicates that K2more loyally accept items and are more likely to count the quest for the player than K1.
And that's all for today.