Issue # 31: IT training - current issues and challenges from leading companies

Questions

There are 1000 wine bottles. One of the bottles contains poisoned wine. A rat dies one hour after drinking the poisoned wine. How many minimum rats are needed to figure out which bottle contains poison in hour.

There are 5 pirates, they must decide how to distribute 100 gold coins among them. The pirates have seniority levels, the senior-most is A, then B, then C, then D, and finally the junior-most is E.

Rules of distribution are:

• The most senior pirate proposes a distribution of coins.
• All pirates vote on whether to accept the distribution.
• If the distribution is accepted, the coins are disbursed and the game ends.
• If not, the proposer is thrown and dies, and the next most senior pirate makes a new proposal to begin the system again.
• In case of a tie vote the proposer can has the casting vote

Rules every pirates follows:

• Every pirate wants to survive
• Given survival, each pirate wants to maximize the number of gold coins he receives.

What is the maximum number of coins that pirate A might get?

Given an integer, the task is to find factorial of the number.

Input:
The first line of input contains an integer T denoting the number of test cases.
The first line of each test case is N, the number whose factorial is to be found

Output:
Print the factorial of the number in separate line.

Constraints: Example: Input Output
1 ≤ T ≤ 100
1 ≤ N ≤ 1000



3
5
10
2


120
3628800
2

Given a Binary Tree, find diameter of it.
+The diameter of a tree is the number of nodes on the longest path between two leaves in the tree. The diagram below shows two trees each with diameter nine, the leaves that form the ends of a longest path are shaded (note that there is more than one path in each tree of length nine, but no path longer than nine nodes).



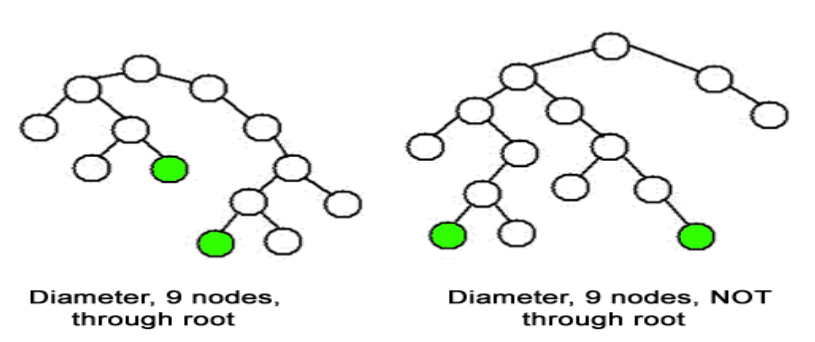
Input Format:
First line of input contains the number of test cases T. For each test case, there will be only a single line of input which is a string representing the tree as described below:

1. The values in the string are in the order of level order traversal of the tree where, numbers denotes node values, and a character “N” denotes NULL child.

2. For example:

For the above tree, the string will be: 1 2 3 NN 4 6 N 5 NN 7 N

Output Format:
For each testcase, in a new line, print the diameter.

Your Task:
You need to complete the function diameter () that takes node as parameter and returns the diameter.

Constraints: Example: Input: Output: Explanation: Testcase1: The tree is The diameter is of 3 length. Testcase2: The tree is The diameter is of 4 length.
1 <= T <= 100
1 <= Number of nodes <= 100
1 <= Data of a node <= 100



2
1 2 3
10 20 30 40 60


3
4

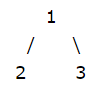
Transfer

, .
+ — . , , , , ( , , ).

:
T. , , , :

1. , , “N” .

2. :

: 1 2 3 N N 4 6 N 5 N N 7 N

:
.

:
diameter(), node .

:
1 < = T <= 100
1 < = < = 100
1 < = <= 100

:
:
2
1 2 3
10 20 30 40 60

:
3
4

:
1: :

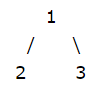
3.
2: :

4 .

How many ways are there to place a black and a white knight on an N * M chessboard such that they do not attack each other? The knights have to be placed on different squares. A knight can move two squares horizontally and one square vertically (L shaped), or two squares vertically and one square horizontally (L shaped). The knights attack each other if one can reach the other in one move.

Input:
The first line contains the number of test cases T. Each of the next T lines contains two integers N and M which is size of matrix.

Output:
For each testcase, print the required answer, i.e, number of possible ways to place knights.

Constraints:
1 <= T <= 100
1 <= N, M <= 105

Example:
Input:
3
2 2
2 3
4 5

Output:
12
26
312
Explanation:
Testcase 1: We can place a black and a white knight in 12 possible ways such that none of them attracts each other.

using namespace boost::multiprecision;
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        cpp_int n, res = 1;
        cin >> n;
        while (n != 1)
        {
            res = res * n;
            n = n - 1;
        }
        cout << res << "\n";
    }
    return 0;
}

int find(Node* root, int &h)
{
    if (root == NULL) return 0;
    int lh = find(root->left, h);
    int rh = find(root->right, h);
    h = max(h, lh + rh + 1);
    return max(lh, rh) + 1;
}
int diameter(Node* root)
{
    int h = -1;
    find(root, h);
    return h;
}

#include <iostream>
#include <cstdint>

typedef unsigned __int128 uint128_t;

/**
 * O(1) solution to https://practice.geeksforgeeks.org/problems/black-and-white/0
 */
int main()
{
    unsigned t;
    uint64_t n, m, upper, lower;
    uint128_t res;
    
    std::cin >> t;
    while (t--)
    {
        std::cin >> n >> m;
        res = n*m; // total ways to choose first knight
        res *= (n*m-1); // now total ways to choose both knights
        if (n>1 && m>1)
            res -= 4*(2*n*m-3*n-3*m+4); // remove any collisions
        
        // the rest is just for printing a uint128_t
        upper = (uint64_t)(res/1000000000000000000);
        lower = (uint64_t)(res%1000000000000000000);
        if (upper)
        {
            std::cout << upper;
            uint64_t digitChecker = 100000000000000000;
            while (lower/digitChecker == 0 && digitChecker)
            {
                std::cout << 0;
                digitChecker /= 10;
            }
        }
        std::cout << lower << std::endl;
    }
    
	return 0;
}