Get best of the week

How are very long integer types implemented in Python?

A translation of the article was prepared specifically for students of the Python Developer course .




When you write in a low-level language such as C, you are worried about choosing the right data type and qualifiers for your integers, at each step you analyze whether it will be enough to use it simply intor whether you need to add longor even long double. However, when writing code in Python, you don’t have to worry about these “minor” things, because Python can work with numbers of integerany size type .

In C, if you try to calculate 2 20000 using the built-in function powl, you will get the output inf.

#include <stdio.h>
#include <math.h>

int main(void) {
  printf("%Lf\n", powl(2, 20000));
  return 0;
}

$ ./a.out
inf

But in Python, making this easier than ever is easy:

>>> 2 ** 20000
39802768403379665923543072061912024537047727804924259387134 ...
...
... 6021 digits long ...
...
6309376

It must be under the hood that Python is doing something very beautiful, and today we will find out what it does to work with integers of arbitrary size!

Presentation and Definition


Integer in Python, this is a C structure defined as follows:

struct _longobject {
    PyObject_VAR_HEAD
    digit ob_digit[1];
};

PyObject_VAR_HEADIs a macro, it expands to PyVarObject, which has the following structure:

typedef struct {
    PyObject ob_base;
    Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;

Other types that have PyObject_VAR_HEAD:

  • PyBytesObject
  • PyTupleObject
  • PyListObject

This means that an integer, like a tuple or a list, has a variable length, and this is the first step to understanding how Python can support work with giant numbers. Once expanded, the macro _longobjectcan be considered as:

struct _longobject {
    PyObject ob_base;
    Py_ssize_t ob_size; /* Number of items in variable part */
    digit ob_digit[1];
};

There PyObjectare some meta fields in the structure that are used for reference counting (garbage collection), but in order to talk about this, we need a separate article. The field on which we will focus this ob_digitand in a bit ob_size.

Decryption ob_digit


ob_digitIs a statically allocated array of unit length of type digit (typedef uint32_t). Since this is an array, it ob_digitis primarily a pointer to a number, and therefore, if necessary, it can be increased using the malloc function to any length. This way python can represent and process very long numbers.

Typically, in low-level languages ​​such as C, the precision of integers is limited to 64 bits, however Python supports integers of arbitrary precision . Starting with Python 3, all numbers are presented in the form bignumand are limited only by the available system memory.

Decryption ob_size


ob_sizestores the number of items in ob_digit. Python overrides and then uses the value ob_sizeto determine the actual number of elements contained in the array to increase the efficiency of allocating memory to the array ob_digit.

Storage


The most naive way to store integer numbers is to store one decimal digit in one element of the array, then operations such as addition and subtraction can be performed according to the rules of mathematics from elementary school.

With this approach, the number 5238 will be saved like this: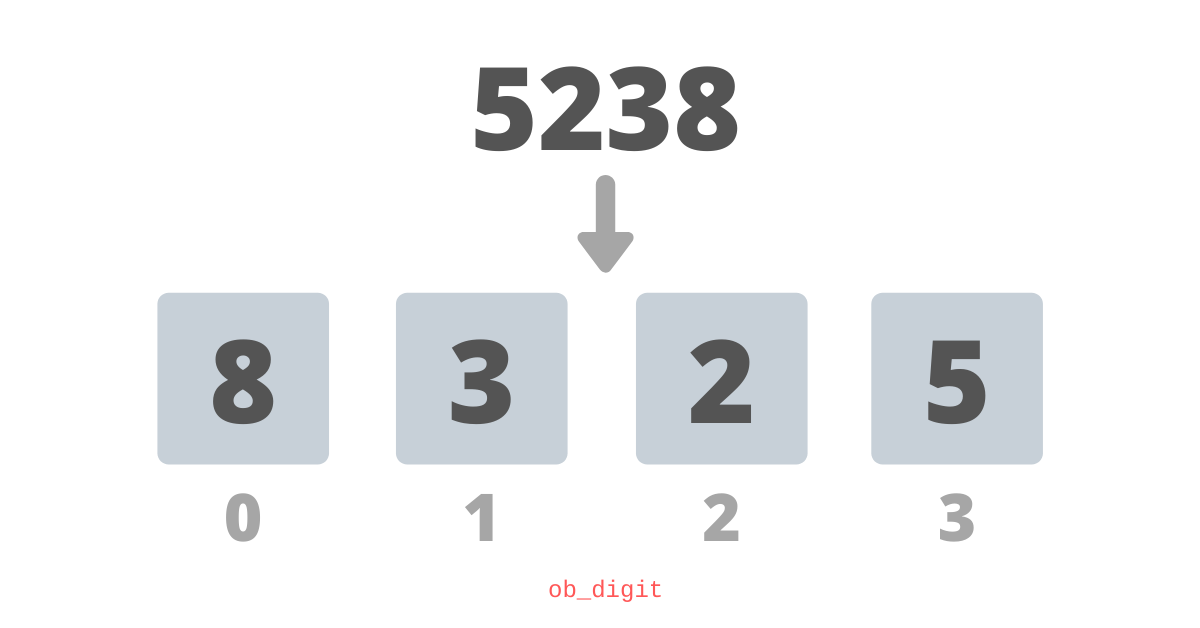



This approach is inefficient, since we will use up to 32-bit digits (uint32_t) to store a decimal digit, which, in fact, ranges from 0 to 9 and can be easily represented with only 4 bits, for when writing something as versatile as python, the kernel developer should be even more inventive.

So, can we do better? Of course, otherwise I would not have posted this article. Let's take a closer look at how Python stores an extra-long integer.

Python path


Instead of storing only one decimal digit in each element of the array ob_digit, Python converts numbers from the number system with a base of 10 to numbers in a system with a base of 2 30 and calls each element as a digit whose value ranges from 0 to 2 30 - 1.

In the hexadecimal number system, the base 16 ~ 2 4 means that each "digit" of the hexadecimal number ranges from 0 to 15 in the decimal number system. In Python, similarly, a “number” with a base of 2 30 , which means that the number will vary from 0 to 2 30 - 1 = 1073741823 in decimal.

Thus, Python effectively uses almost all of the allocated space of 32 bits per digit, saves resources, and still performs simple operations such as addition and subtraction at the math level of elementary school.

Depending on the platform, Python uses either 32-bit unsigned integer arrays or 16-bit unsigned integer arrays with 15-bit digits. To perform the operations that will be discussed later, you need only a few bits.

Example: 1152921504606846976

As mentioned, for Python, numbers are represented in a base 2 30 system , that is, if you convert 1152921504606846976 into a base number with 2 30 base , you get 100.

1152921504606846976 = 1 * (2 30) 2 + 0 * (2 30 ) 1 + 0 * (2 30 ) 0

Since the ob_digitleast significant digit is stored first, it is saved as 001 as three digits.

The structure _longobjectfor this value will contain:

  • ob_size like 3
  • ob_digit like [0, 0, 1]



I created a demo REPL that will show how Python stores an integer inside itself, and also refers to structure members such as ob_size, ob_refcountetc.

Integer Long Operations


Now that we have a clear idea of ​​how Python implements integers of arbitrary precision, it is time to understand how various mathematical operations are performed with them.

Addition


Integers are stored "in numbers", which means that addition is as simple as in elementary school, and the Python source code shows us that this is how addition is implemented. A function with a name x_addin a file longobject.cadds two numbers.

...
    for (i = 0; i < size_b; ++i) {
        carry += a->ob_digit[i] + b->ob_digit[i];
        z->ob_digit[i] = carry & PyLong_MASK;
        carry >>= PyLong_SHIFT;
    }
    for (; i < size_a; ++i) {
        carry += a->ob_digit[i];
        z->ob_digit[i] = carry & PyLong_MASK;
        carry >>= PyLong_SHIFT;
    }
    z->ob_digit[i] = carry;
...

The code snippet above is taken from a function x_add. As you can see, it iterates over a number by numbers and performs the addition of numbers, calculates the result and adds hyphenation.

It becomes more interesting when the result of addition is a negative number. The sign ob_sizeis an integer sign, that is, if you have a negative number, then it ob_sizewill be a minus. The value ob_sizemodulo will determine the number of digits in ob_digit.

Subtraction


Just as addition takes place, subtraction also takes place. A function with a name x_subin the file longobject.csubtracts one number from another.

...
    for (i = 0; i < size_b; ++i) {
        borrow = a->ob_digit[i] - b->ob_digit[i] - borrow;
        z->ob_digit[i] = borrow & PyLong_MASK;
        borrow >>= PyLong_SHIFT;
        borrow &= 1; /* Keep only one sign bit */
    }
    for (; i < size_a; ++i) {
        borrow = a->ob_digit[i] - borrow;
        z->ob_digit[i] = borrow & PyLong_MASK;
        borrow >>= PyLong_SHIFT;
        borrow &= 1; /* Keep only one sign bit */
    }
...

The code snippet above is taken from a function x_sub. In it, you see how the enumeration of numbers occurs and subtraction is performed, the result is calculated and the transfer is distributed. Indeed, it is very similar to addition.

Multiplication


And again, the multiplication will be implemented in the same naive way that we learned from the lessons of mathematics in elementary school, but it is not very efficient. To maintain efficiency, Python implements the Karatsuba algorithm , which multiplies two n-digit numbers in O (n log 2 3 ) simple steps.

The algorithm is not simple and its implementation is beyond the scope of this article, but you can find its implementation in functions k_mul and k_lopsided_mulin the file longobject.c.

Division and other operations


All operations on integers are defined in the file longobject.c, they are very simple to find and trace the work of each. Attention: A detailed understanding of the work of each of them will take time, so pre-stock up with popcorn .


Python preallocates a small number of integers in memory ranging from -5 to 256. This allocation occurs during initialization, and since we cannot change the integers (immutability), these pre-allocated numbers are singleton and are directly referenced instead of being allocated. This means that every time we use / create a small number, Python instead of selling it simply returns a reference to the previously allocated number.

Such optimization can be traced in the macro IS_SMALL_INTand function get_small_intc longobject.c. So Python saves a lot of space and time in calculating commonly used integer numbers.

This is the second article in the Python Internals series. The first article was about how I changed my version of Python to make itambiguous . It will help you take the first steps in understanding the Python source code and continue the path to becoming a Python kernel developer.

If you want to see more similar articles, subscribe to my newsletter and receive them directly in your inbox. I write about engineering, systems engineering and a little about programming every Friday. Email me at @arpit_bhayani . You can find my previous articles on @ arpitbhayani.me / blogs .

That's all. See you on the course !

More articles:


All Articles