People meet recommender systems. Factorization

Machine learning has pretty much penetrated our everyday lives. Some are no longer surprised when they are told about neural networks in their smartphones. One of the big areas in this science is recommendation systems. They are everywhere: when you listen to music, read books, watch TV shows or videos. The development of this science takes place in giant companies such as YouTube , Spotify and Netfilx . Of course, all scientific achievements in this area are published both at the famous NeurIPS or ICML conferences , and at the slightly less well-known RecSyssharpened on this subject. And in this article we will talk about how this science developed, what methods are used in the recommendations then and now, and what mathematics is behind all this.

I was inspired to write this article by working in the StatML lab at Skoltech related to recommender systems.

Why and for whom this article

Why can this be important for each of us? Take a look at the list below:

• Video recommendations: YouTube, Netlix, HBO, Amazon Prime, Disney +, Hulu, Okko
• Audio recommendations: Spotify, Yandex.Music, Yandex.Radio, Apple Music
• Product Recommendations: Amazon, Avito, LitRes, MyBook
• Search recommendations: Google, Yandex, Bing, Yahoo, Mail
• : Booking, Twitter, Instagram, ., , GitHub

, . , . , , YouTube.

( ), . , , . , ( ). -, . , -, , - . , . , , , , .

, , , , - . , (, , , ..). , .

, . : $$$U$ $$$I$ — . $$$r_{ui}$ $$$u$ $$$i$. , , , , . :

$$

$$\mathcal{D} = \{ (u, i) |\text{ if } \exists r_{ui}, u \in U, i \in I\}$$

$$$f$:

$$

$$f(u, i) = \hat{r}_{ui}\approx r_{ui}$$

, $$$r_{ui}$ 1 5 ( ) : 1 -1 ( / )

3 :

• Content-based (CB)
• Collaborative filtering (CF)
• Hybrid recommendations

. — , . : — , — , . . , : , ..

, . - , .

. , , , .

, , . . , , . .

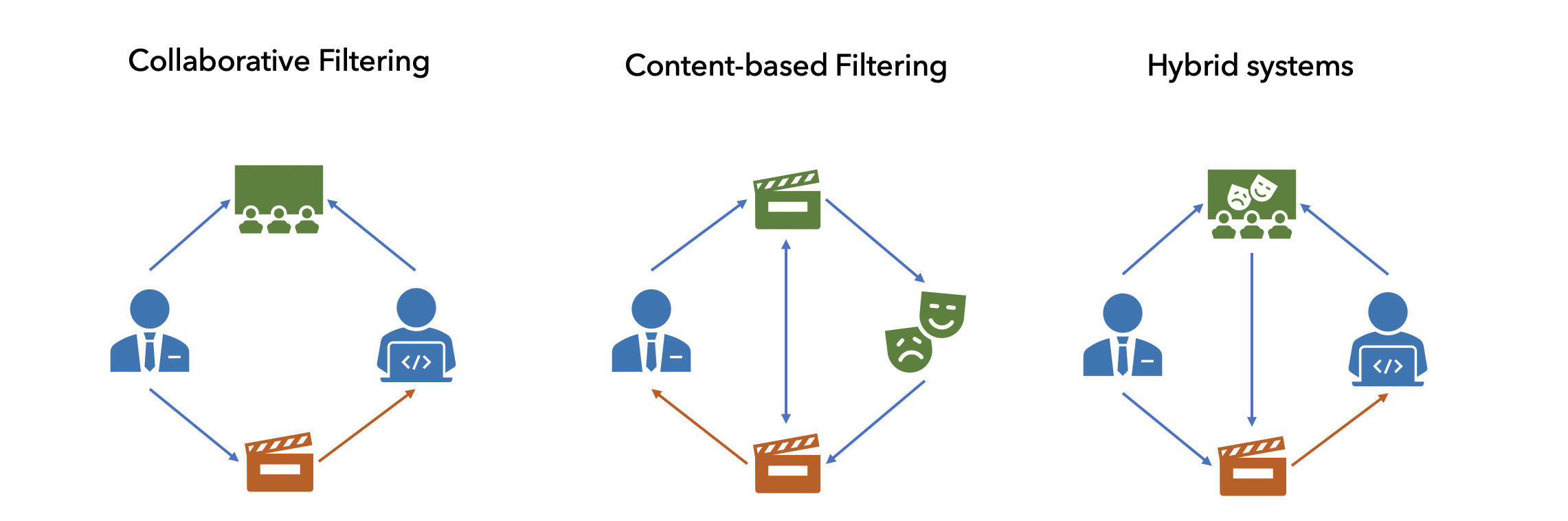
Matrix Factorization

, . : . .

• :
  
  • Singular Value Decomposition (SVD)
  • Singular Value Decomposition with implicit feedback (SVD++)
  • Collaborative Filtering with Temporal Dynamics (TimeSVD++)
  • Weighted Matrix Factorization (WMF or ALS)
  • Sparse Linear Methods (SLIM)
  • Factorization Machines (FM)
• :
  
  • Probabilistic Matrix Factorization (PMF)
  • Bayesian Probabilistic Matrix Factorization (BPMF)
  • Bayesian Factorization Machines (BFM)
  • Gaussian Process Factorization Machines (GPFM)

Singular Value Decomposition (SVD)

— SVD. $$$A$ $$$n \times m$, $$$n = |U|$, $$$m = |I|$. $$$\mathcal{D}$ $$$A_{ui} = r_{ui}$, . SVD , $$$A$ : $$$U,~\Sigma,~V$. $$$k$ , $$$A$.

$$

$$A = U \Sigma V^T, \quad\quad\quad\quad A \approx \hat{A} = \hat{U} \hat{ \Sigma } \hat{V}^T .$$

$$$Q$ $$$P$ . $$$A$ :

$$

$$P = (\hat{U} \hat{ \Sigma })^T, \quad\quad Q = \hat{V}^T, \quad\quad\quad\quad A \approx P^T \cdot Q .$$

:

$$

$$r_{ui} \approx \hat{r}_{ui} = p^T_u q_i .$$

, $$$p_u$ $$$q_i$ — $$$u$ $$$i$ - $$$k$. . . :

$$

$$\Theta = \{ p_u, q_i| u \in U, i \in I\} .$$

c :

$$

$$\sum_{(u, i) \in \mathcal{D}} (r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 = \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p^T_u q_i)^2 + \lambda\sum_{u \in U}\|p_u\|^2 + \lambda\sum_{i \in I}\|q_i\|^2 .$$

, , , , . $$$\hat{r}_{ui}$. (GD) (ALS). Habr- , . , , .

( SVD, SVD$$$_{bias}$). , , . . SVD . (bias):

$$

$$\hat{r}_{ui} =\mu + b_u + b_i + p^T_u q_i ,$$

$$$b_u$ — , $$$b_i$ — , $$$\mu$ — . :

$$

$$\Theta = \{ \mu, b_u, b_i, p_u, q_i| u \in U, i \in I\} .$$

SVD++

Factorization Meets the Neighborhood SVD . (explicit and implicit user feedback). $$$r_{ui}$, . . : $$$R(u)$ — ( ) $$$N(u)$ — ( ).

SVD++ :

$$

$$\hat{r}_{ui} =\mu + b_u + b_i + q^T_i \left( p_u + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) .$$

:

$$

$$\Theta = \{ \mu, b_u, b_i, p_u, q_i, y_i| u \in U, i \in I\} .$$

, $$$N(u)$ $$$R(u)$, .. $$$R(u) \subset N(u)$. (item-item recommendation).

Asymmetric-SVD

SVD++ . . :

$$

$$\hat{r}_{ui} = b_{ui} + q^T_i \left( |R(u)|^{-1/2} \sum_{j \in R(u)} (r_{uj} - b_{uj})x_j + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) ,$$

$$$b_{ui} = \mu + b_u + b_i$

TimeSVD++

TimeSVD++. (MovieLens, Netflix) , . , . Collaborative Filtering with Temporal Dynamics SVD++ :

$$

$$\hat{r}_{ui}(t) =\mu + b_u(t) + b_i(t) + q^T_i \left( p_u(t) + |R(u)|^{-1/2} \sum_{j \in R(u)} y_j \right) .$$

Let's figure out how exactly the time affects each term:
Item bias: If you divide the time interval when the ratings were put into segments (30 parts are proposed in the work) and add your own parameters$$$b_{i,\text{Bin}(t)}$ for each product, which are selected depending on the interval in which the variable $$$t$:

$$

$$b_i(t) = b_i + b_{i, \text{Bin}(t)}$$

User bias: Analyzing the data of Neflix, we noticed that for each user on average there are only 40 days in which he put the ratings. Therefore, we will act as with goods and add our own parameters$$$b_{u, t}$for each user. We add a linear dependence on time - we introduce an additional term$$$\alpha_u$ with depreciation ratio:

$$

$$b_i(t) = b_i + \alpha_u \cdot \text{dev}_u(t) + b_{u, t} \quad\quad\quad\quad \text{dev}_u(t) = \text{sign}(t - t_u) \cdot |t - t_u|^{\beta}$$

.
There are other options on how to add a time dependency to users: It is described in more detail in the article
User embeddings: we will add a similar trick for each component of our latent representation$$$p_u(t) = (p_{u1}(t), \dots, p_{uf}(t))^T$:

$$

$$p_{uk}(t) = p_{uk} + \alpha_{uk} \cdot \text{dev}_u(t) + p_{uk, t}.$$

Weighted Matrix Factorization (WMF) & Alternating Least Squares (ALS)

One of the main problems that SVD has is the use of only an explicit response from the user. This problem was partially solved in SVD ++ . But there is another way - Weighted Matrix Factorization ( WMF ). In this article, they suggested almost not changing the model ($$$\hat{r}_{ui} = p^T_u q_i$), and change the learning process. Assign for ratings$$$r_{ui}$that we don’t know (i.e. for couples $$$(u, i) \notin \mathcal{D}$) the value is 0. And then for each pair $$$(u, i)$ enter the parameter $$$c_{ui}$, $$$r_{ui}$. , . - . YouTube , . , , , . , , , :

$$

$$\sum_{(u, i)} c_{ui}(r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 .$$

: $$$c_{ui} = 1 + \alpha r_{ui}$. : $$$r_{ui}>0$ $$$r_{ui} = 0$. $$$\alpha$ $$$\alpha = 40$ .

, (ALS) . WMF, ALS, .

Fast Alternating Least Squares

ALS , eALS . , . , . .

, $$$c_{ui}$ ALS :

$$

$$c_{ui} = c_i + \alpha r_{ui}, \quad\quad\quad\quad c_i = c_0 \frac{f_i^{\beta}}{\sum_{j \in I} f_j^{\beta}} ,$$

$$$c_0$ $$$\beta$, .

Sparse Linear Methods (SLIM)

Sparse Linear Methods (SLIM) . , SVD . . SLIM :

$$

$$\hat{a}_{ui} = a^T_u w_i \quad\quad\quad\quad \hat{A} = AW$$

$$$W \in \mathbb{R}^{m \times m}$. : $$$W \geq 0$ $$$\text{diag}(W) = 0$. :

$$

$$\frac{1}{2}\|A - AW\|^2_F + \frac{\beta}{2}\|W\|^2_F + \lambda\|W\|_1$$

$$$W$ .

Factorization Machines (FM)

, Factorization Machines (FM). , ( 2- ). :

$$

$$\hat{r}(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{i=j+1}^{n} v^T_i v_j ~ x_i x_j, \quad\quad\quad\quad w_0 \in \mathbb{R} ~~~ w \in \mathbb{R}^n ~~~ V \in \mathbb{R}^{n \times k} .$$

(SGD) ( ). , $$$x$ $$$(u, i)$. . , — . — ( ). ( ).

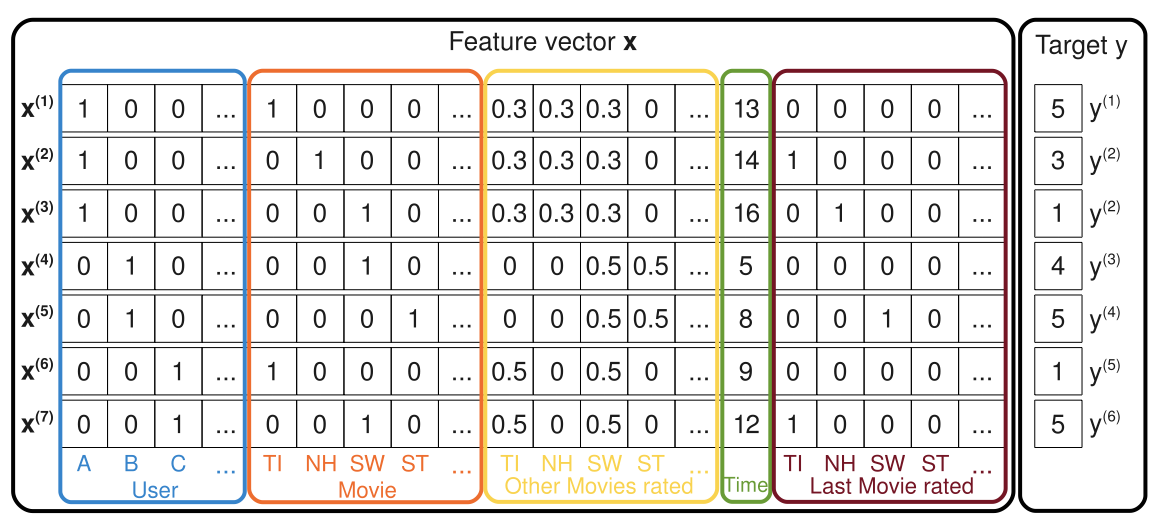
, SVD, SVD++ — FM. SVD , :

$$

$$n = | U \cup I |, \quad\quad\quad x_j = \delta (j = u ~\lor~ j = i) .$$

$$$\delta$ — . .. $$$x$ $$$u$ $$$i$. FM :

$$

$$\hat{r}(x) = w_0 + w_u + w_i + v^T_u v_i .$$

, $$$x$: , . , , , , , , . .

Probabilistic Matrix Factorization (PMF)

, , , .

(PMF), . , SVD: $$$p_u$ $$$q_i$ — . , :

$$

$$p(r | P, Q, \sigma) = \prod_{(u, i) \in \mathcal{D}}\mathcal{N}(r_{ui}| g(p_u^Tq_i), \sigma^2) ,$$

$$$\mathcal{N}$ — , a $$$g(x) = \frac{1}{1 + e^{-x}}$ — (). , , :

$$

$$p(P| \sigma_p) = \prod_{u \in U} p(p_u| 0, \sigma^2_p \mathbf{I}), \quad\quad\quad\quad p(Q| \sigma^2_q) = \prod_{i \in I} p(q_i| 0, \sigma_q^2 \mathbf{I}) .$$

( ) , :

$$

$$\frac{1}{2} \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p_u^T q_i)^2 + \frac{\lambda_p}{2} \sum_{u \in U} \|p_u\|^2 + \frac{\lambda_q}{2} \sum_{i \in I} \|q_i\|^2 ,$$

$$$\lambda_p = \frac{\sigma_p}{\sigma}$ $$$\lambda_q = \frac{\sigma_q}{\sigma}$ — . , SVD , .

Constrained PMF

PMF Constrained PMF. , SVD SVD++. , , $$$p_u$ :

$$

$$p_u + \frac{\sum_{i \in R(u)} y_i}{|R(u)|} ,$$

$$$R(u)$ — , $$$u$.

Bayesian Probabilistic Matrix Factorization (BPMF)

PMF BPMF. PMF , , . :

$$

$$p(P| \mu_p, \Lambda_p) = \prod_{u \in U} p(p_u| \mu_p, \Lambda_p) ,\quad\quad\quad\quad p(Q| \mu_q, \Lambda_q) = \prod_{i \in I} p(q_i| \mu_q, \Lambda_q) .$$

$$$\Theta_p = \{ \mu_p, \Lambda_p \}$ $$$\Theta_q = \{ \mu_q, \Lambda_q \}$ - $$$\Theta_0 = \{ \mu_0, \nu_0, W_0 \}$. , .

Bayesian Factorization Machines (BFM)

, Bayesian, . , $$$\Theta = \{ w_0, w_i, v_i\} .$ , - . : $$$\Theta_H = \{ \lambda_{\theta}, \mu_{\theta} | \theta \in \Theta \}$. .

Gaussian Process Factorization Machines (GPFM)

GPFM . $$$f$ $$$\theta$. $$$\theta_u$ , , :

$$

$$\hat{r}_{ui} = f(q_i, \theta_u)$$

, . , $$$f$ , . , , , .

.

: Bayesian Personalized Ranking (BPR)

BPR , "". , BPR — , , Bayesian Personalized Ranking. . , , $$$i$ $$$j$ $$$u$. $$$(u, i)$ $$$r_{ui}$ $$$(u, i, j)$ $$$i$ $$$j$ ((+) $$$i$ , $$$j$ (-) ). $$$\mathcal{D}_S$. . ( personalized ):

$$

$$p(i <_u j | \Theta) = \sigma(\hat{r}_{uij}(\Theta)) ,$$

$$$\sigma$ — , a $$$\hat{r}_{uij}$ — . (MLE), , :

$$

$$\min_{\Theta} \sum_{(u, i, j) \in \mathcal{D}_S}\ln{\sigma(\hat{r}_{uij})} - \lambda \|\Theta\|^2$$

(SGD):

$$

$$\Theta \leftarrow \Theta + \alpha\left(\frac{e^{-\hat{r}_{uij}}}{1 + e^{-\hat{r}_{uij}}} \cdot \frac{\partial}{\partial \Theta}\hat{r}_{uij} + \lambda \Theta \right)$$

, . , , . SVD:

$$

$$\hat{r}_{uij} = \hat{r}_{ui} - \hat{r}_{uj} \quad\quad\quad\quad \hat{r}_{ui} = p_u^T q_i$$

:

$$

$$\frac{\partial}{\partial \Theta}\hat{r}_{uij} =\begin{cases} (q_{ik} - q_{jk})~~~\text{if } \theta = p_{uk}\\ p_{uk}~~~~~~~~~~~~~~~\text{if } \theta = q_{ik}\\ -p_{uk}~~~~~~~~~~~~\text{if } \theta = q_{jk} \end{cases}$$

BPR ( ) , . , . . , (pairwise approach) (pointwise approach). . , 5 , . , , . — BPR - , . , .

Show must go on

This time we discussed many Factorization methods in recommendation systems, but the Graph and Neural Networks , which also have a lot of interesting things , remained untouched .