Schönen Tag.Ich präsentiere Ihnen die Übersetzung des Artikels „Algorithmen in Graphen: Sprechen wir über die Tiefensuche (DFS) und die Breitensuche (BFS)“ von Try Khov.Was ist eine Graphenüberquerung?
Mit einfachen Worten, eine Diagrammdurchquerung ist ein Übergang von einem ihrer Scheitelpunkte zu einem anderen auf der Suche nach den Verbindungseigenschaften dieser Scheitelpunkte. Verknüpfungen (Linien, die Scheitelpunkte verbinden) werden als Richtungen, Pfade, Flächen oder Kanten eines Diagramms bezeichnet. Die Eckpunkte des Graphen werden auch als Knoten bezeichnet.Die beiden Hauptalgorithmen für das Durchlaufen von Graphen sind die Tiefensuche (DFS) und die Breitensuche (BFS).Trotz der Tatsache, dass beide Algorithmen zum Durchlaufen des Graphen verwendet werden, weisen sie einige Unterschiede auf. Beginnen wir mit DFS.Tiefensuche
Die DFS folgt dem Konzept „tief gehen, mit dem Kopf voran“. Die Idee ist, dass wir uns vom Startgipfel (Punkt, Ort) in eine bestimmte Richtung (entlang eines bestimmten Pfades) bewegen, bis wir das Ende des Pfades oder Ziels (gewünschter Gipfel) erreichen. Wenn wir das Ende des Pfades erreicht haben, es aber kein Ziel ist, kehren wir zurück (bis zu verzweigten oder divergierenden Pfaden) und gehen einen anderen Weg.Schauen wir uns ein Beispiel an. Angenommen, wir haben einen gerichteten Graphen, der so aussieht:
Wir befinden uns am Punkt „s“ und müssen den Scheitelpunkt „t“ finden. Mit DFS untersuchen wir einen der möglichen Pfade, bewegen uns bis zum Ende und gehen zurück, wenn wir t nicht finden, und erkunden einen anderen Pfad. So sieht der Prozess aus:
Hier bewegen wir uns entlang des Pfades (p1) zum nächsten Gipfel und sehen, dass dies nicht das Ende des Pfades ist. Deshalb fahren wir mit dem nächsten Gipfel fort.
Wir haben das Ende von p1 erreicht, aber t nicht gefunden, also kehren wir zu s zurück und bewegen uns auf dem zweiten Pfad.
Nachdem wir die Spitze des Pfades „p2“ erreicht haben, der dem Punkt „s“ am nächsten liegt, sehen wir drei mögliche Richtungen für die weitere Bewegung. Da wir bereits den Gipfel besucht haben, der die erste Richtung krönt, bewegen wir uns entlang der zweiten.
Wir erreichten wieder das Ende des Weges, fanden aber t nicht und gingen zurück. Wir folgen dem dritten Weg und erreichen schließlich den gewünschten Gipfel "t".
So funktioniert DFS. Wir bewegen uns auf einem bestimmten Weg bis zum Ende. Wenn das Ende des Pfades der gewünschte Peak ist, sind wir fertig. Wenn nicht, gehen Sie zurück und gehen Sie einen anderen Weg, bis wir alle Optionen untersucht haben.Wir folgen diesem Algorithmus für jeden besuchten Scheitelpunkt.Die Notwendigkeit einer wiederholten Wiederholung der Prozedur zeigt die Notwendigkeit einer Rekursion an, um den Algorithmus zu implementieren.Hier ist der JavaScript-Code:
function dfs(adj, v, t) {
if(v === t) return true
if(v.visited) return false
v.visited = true
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
let reached = dfs(adj, neighbor, t)
if(reached) return true
}
}
return false
}
Hinweis: Mit diesem speziellen DFS-Algorithmus können Sie überprüfen, ob es möglich ist, von einem Ort zum anderen zu gelangen. DFS kann für verschiedene Zwecke verwendet werden. Diese Ziele bestimmen, wie der Algorithmus selbst aussehen wird. Das allgemeine Konzept sieht jedoch genau so aus.DFS-Analyse
Lassen Sie uns diesen Algorithmus analysieren. Da wir jeden „Nachbarn“ jedes Knotens umgehen und die zuvor besuchten ignorieren, haben wir eine Laufzeit von O (V + E).Eine kurze Erklärung, was V + E bedeutet:V ist die Gesamtzahl der Eckpunkte. E ist die Gesamtzahl der Flächen (Kanten).Es mag angemessener erscheinen, V * E zu verwenden, aber lassen Sie uns darüber nachdenken, was V * E bedeutet.V * E bedeutet, dass wir in Bezug auf jeden Scheitelpunkt alle Flächen des Graphen untersuchen müssen, unabhängig davon, ob diese Flächen zu einem bestimmten Scheitelpunkt gehören.Andererseits bedeutet V + E, dass wir für jeden Scheitelpunkt nur die angrenzenden Kanten auswerten. Zurück zum Beispiel: Jeder Scheitelpunkt hat eine bestimmte Anzahl von Flächen. Im schlimmsten Fall gehen wir um alle Scheitelpunkte (O (V)) herum und untersuchen alle Flächen (O (E)). Wir haben V Eckpunkte und E Flächen, also erhalten wir V + E.Da wir die Rekursion verwenden, um jeden Scheitelpunkt zu durchlaufen, bedeutet dies, dass ein Stapel verwendet wird (unendliche Rekursion führt zu einem Stapelüberlauffehler). Daher ist die räumliche Komplexität O (V).Betrachten Sie nun das BFS.Breite Suche
BFS folgt dem Konzept "weit ausdehnen und auf die Höhe eines Vogelfluges steigen" ("weit gehen, Vogelperspektive"). Anstatt sich auf einem bestimmten Weg bis zum Ende zu bewegen, muss bei BFS jeweils ein Nachbar vorwärts bewegt werden. Dies bedeutet Folgendes:Anstatt dem Pfad zu folgen, bedeutet BFS, die Nachbarn, die s am nächsten liegen, in einer einzigen Aktion (Schritt) zu besuchen und dann die Nachbarn der Nachbarn usw. zu besuchen, bis t erkannt wird.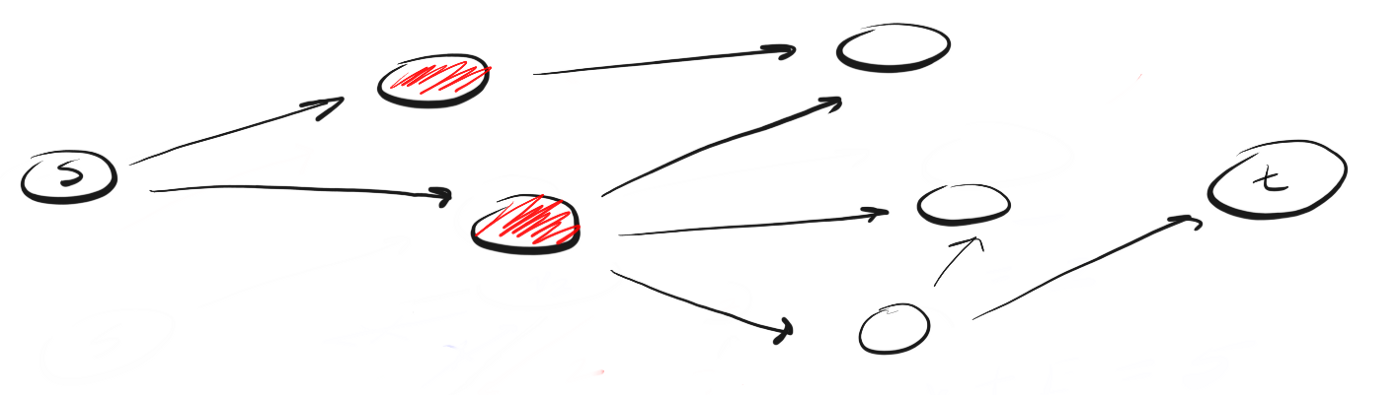
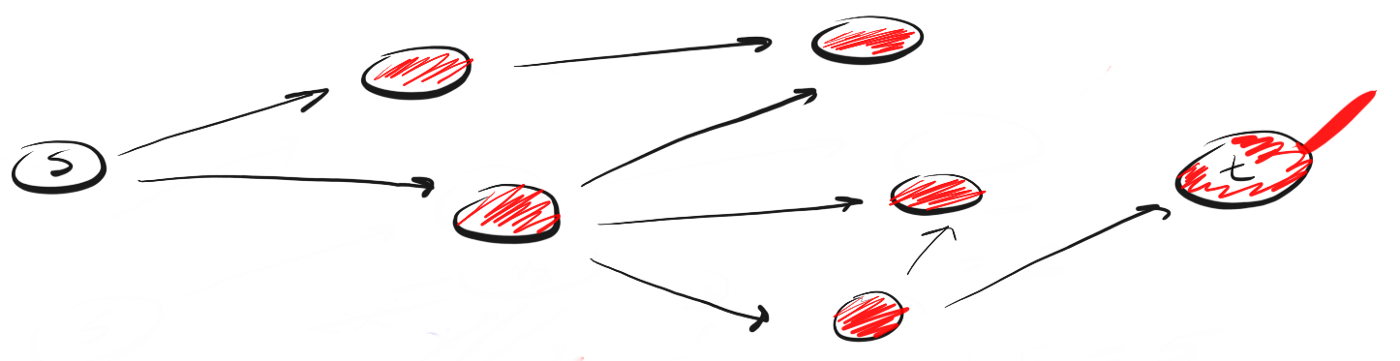Wie unterscheidet sich DFS von BFS? Ich denke gerne, dass die DFS voranschreitet und die BFS es nicht eilig hat, sondern alles in einem Schritt studiert.Dann stellt sich die Frage: Woher wissen Sie, welche Nachbarn zuerst besucht werden sollten?Dazu können wir das Konzept "First In, First Out" (First-In-First-Out, FIFO) aus der Warteschlange verwenden. Wir stellen zuerst den Peak in die Warteschlange, der uns am nächsten liegt, dann die nicht besuchten Nachbarn und setzen diesen Vorgang fort, bis die Warteschlange leer ist oder bis wir den gesuchten Scheitelpunkt finden.Hier ist der Code:
function bfs(adj, s, t) {
let queue = []
queue.push(s)
s.visited = true
while(queue.length > 0) {
let v = queue.shift()
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
queue.push(neighbor)
neighbor.visited = true
if(neighbor === t) return true
}
}
}
return false
}
BFS-Analyse
Es scheint, dass BFS langsamer ist. Wenn Sie sich die Visualisierungen jedoch genau ansehen, können Sie feststellen, dass sie dieselbe Laufzeit haben.In einer Warteschlange wird jeder Scheitelpunkt verarbeitet, bevor ein Ziel erreicht wird. Dies bedeutet, dass BFS im schlimmsten Fall alle Scheitelpunkte und Flächen untersucht.Trotz der Tatsache, dass BFS möglicherweise langsamer erscheint, ist es tatsächlich schneller, da bei der Arbeit mit großen Diagrammen festgestellt wird, dass DFS viel Zeit damit verbringt, Pfaden zu folgen, die sich letztendlich als falsch herausstellen. BFS wird häufig verwendet, um den kürzesten Weg zwischen zwei Spitzen zu finden.Somit ist die BFS-Laufzeit auch O (V + E), und da wir eine Warteschlange verwenden, die alle Eckpunkte enthält, ist ihre räumliche Komplexität O (V).Analogien aus dem wirklichen Leben
Wenn Sie Analogien aus dem wirklichen Leben geben, dann stelle ich mir die Arbeit von DFS und BFS so vor.Wenn ich an DFS denke, stelle ich mir eine Maus in einem Labyrinth auf der Suche nach Nahrung vor. Um zum Ziel zu gelangen, muss die Maus viele Male in eine Sackgasse geraten, zurückkehren und sich auf andere Weise bewegen usw., bis sie einen Weg aus dem Labyrinth oder der Nahrung findet.
Eine vereinfachte Version sieht folgendermaßen aus:
Wenn ich an BFS denke, stelle ich mir wiederum Kreise auf dem Wasser vor. Das Fallen eines Steins ins Wasser führt zur Ausbreitung von Störungen (Kreisen) in alle Richtungen vom Zentrum aus.
Eine vereinfachte Version sieht folgendermaßen aus:
Ergebnisse
- Tiefen- und Breitensuche werden verwendet, um das Diagramm zu durchlaufen.
- DFS bewegt sich entlang der Kanten hin und her, und BFS verteilt sich auf der Suche nach einem Ziel auf die Nachbarn.
- DFS verwendet den Stapel und BFS die Warteschlange.
- Die Laufzeit von beiden ist O (V + E) und die räumliche Komplexität ist O (V).
- Diese Algorithmen haben eine andere Philosophie, sind aber für die Arbeit mit Grafiken gleichermaßen wichtig.
Hinweis Per .: Ich bin kein Spezialist für Algorithmen und Datenstrukturen. Wenn daher Fehler, Ungenauigkeiten oder falsche Formulierungen festgestellt werden, schreiben Sie bitte zur Korrektur und Klärung in einen persönlichen Brief. Ich werde dankbar sein.Vielen Dank für Ihre Aufmerksamkeit.