Ein einfaches Beispiel für eine Clusteranalyse der Alkoholpräferenzen nach Ländern für R.

Hallo Habr! Heute möchte ich ein kleines Beispiel für die Durchführung von Clusteranalysen geben. In diesem Beispiel findet der Leser keine neuronalen Netze und andere modische Richtungen. Dieses Beispiel kann als Referenzpunkt dienen, um eine kleine und vollständige Clusteranalyse für andere Daten durchzuführen. Alle Interessierten - willkommen bei cat.

Wenn Sie sofort einen Vorbehalt machen, erhebt dieser Artikel in keiner Weise den Anspruch, in seiner Gesamtheit, der Einzigartigkeit der erzielten Ergebnisse oder der Vollständigkeit der Berichterstattung über das Thema akademisch zu sein. Der Artikel soll die grundlegenden Schritte der klassischen Clusteranalyse demonstrieren, die für einfache und aussagekräftige (möglicherweise vor einer detaillierteren) Studie verwendet werden können. Korrekturen, Kommentare und Ergänzungen in der Sache sind willkommen.

Die Daten sind eine Stichprobe des Alkoholkonsums pro Land pro Kopf nach Art der alkoholischen Getränke (Bier, Wein, Spirituosen usw.) für 2010 als Prozentsatz des Pro-Kopf-Alkoholkonsums. Die Daten enthalten außerdem: den durchschnittlichen täglichen Alkoholkonsum pro Kopf in Gramm reinem Alkohol und den gesamten (erfassten + nicht erfassten) Alkoholkonsum pro Kopf (nur Trinker in Litern reinem Alkohol).

Gleichzeitig gehört jedes Land bedingt zu einer der geografischen Gruppen: Ost, Mitte und West. Die Aufteilung ist aus verschiedenen Gründen sehr willkürlich und sehr kontrovers, aber wir werden von dem ausgehen, was wir haben. Datenquelle - Globaler Statusbericht zu Alkohol und Gesundheit 2014, S. 289-364

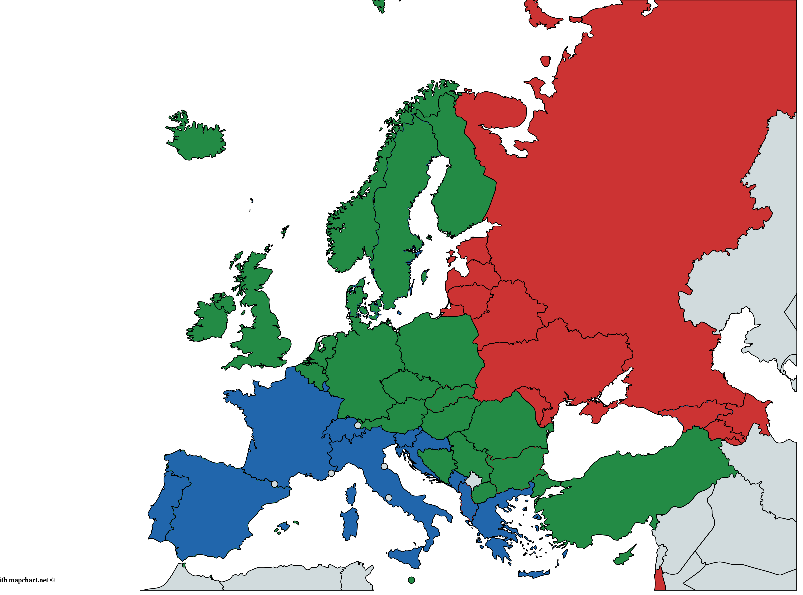
(Handbemalt, es kann Fehler geben, aber die allgemeine Idee, denke ich, ist verständlich)

Voruntersuchung

Verbinden Sie die verwendeten Bibliotheken.

library(rgl)
library(heplots)
library(MVN)
library(klaR)
library('Morpho')
library(caret)
library(mclust)
library(ggplot2)
library(GGally)
library(plyr)
library(psych)
library(GPArotation)
library(ggpubr)

, .

#    
data <- read.table("alcohol_data.csv", header=TRUE,  sep=",")
#      
rownames(data) <- make.names(data[,1], unique = TRUE)
#     ,   
data <- data[,-1]
data <- na.omit(data)
#    
head(data)

summary(data)

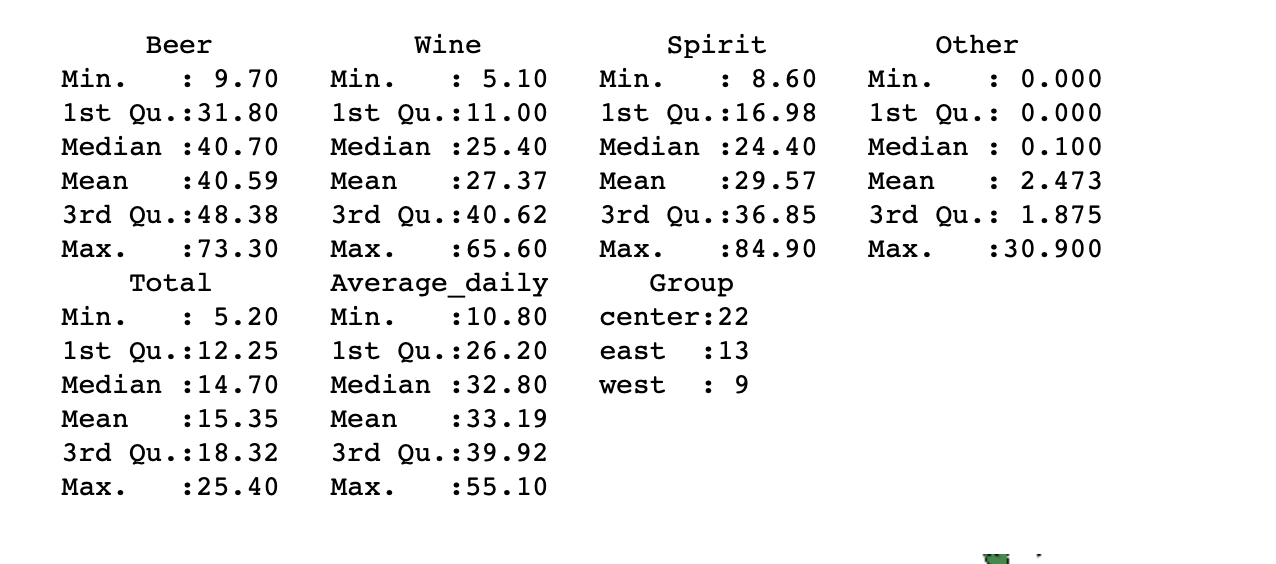
, . , Other , , , , . , , , , . , . - .

, , , .

options(rgl.useNULL=TRUE)
open3d()
mfrow3d(2,2)
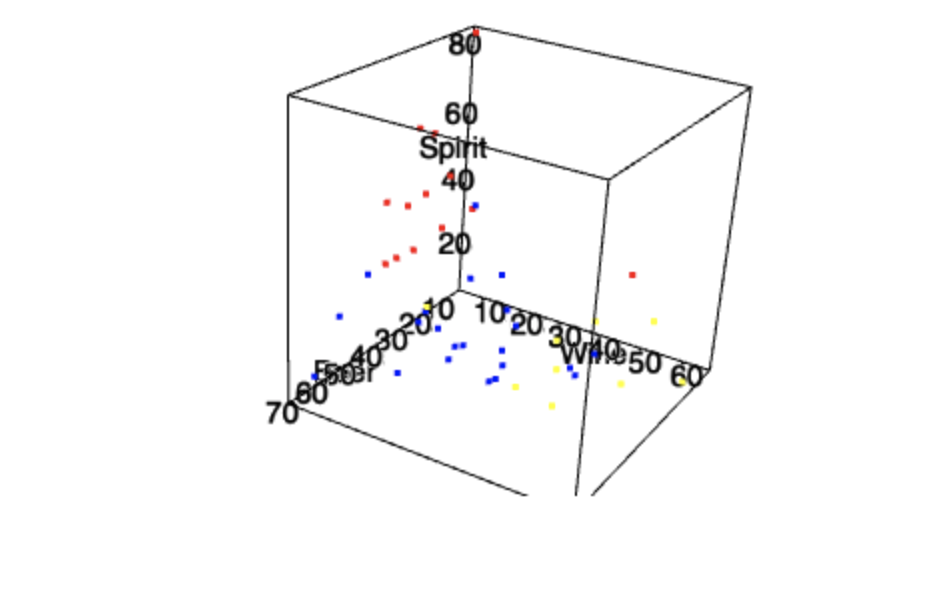
levelColors <- c('west'='blue', 'east'='red', 'center'='yellow')
plot3d(data$Beer, data$Wine, data$Spirit, xlab="Beer", ylab="Wine", zlab="Spirit", col = levelColors[data$Group], size=3)

widget <- rglwidget()
widget

, . , .

ggpairs(
  data,
  mapping = ggplot2::aes(color = data$Group),
  upper = list(continuous = wrap("cor", alpha = 0.5), combo = "box"),
  lower = list(continuous = wrap("points", alpha = 0.3), combo = wrap("dot", alpha = 0.4)),
  diag = list(continuous = wrap("densityDiag",alpha = 0.5)),
  title = "Alcohol"
)

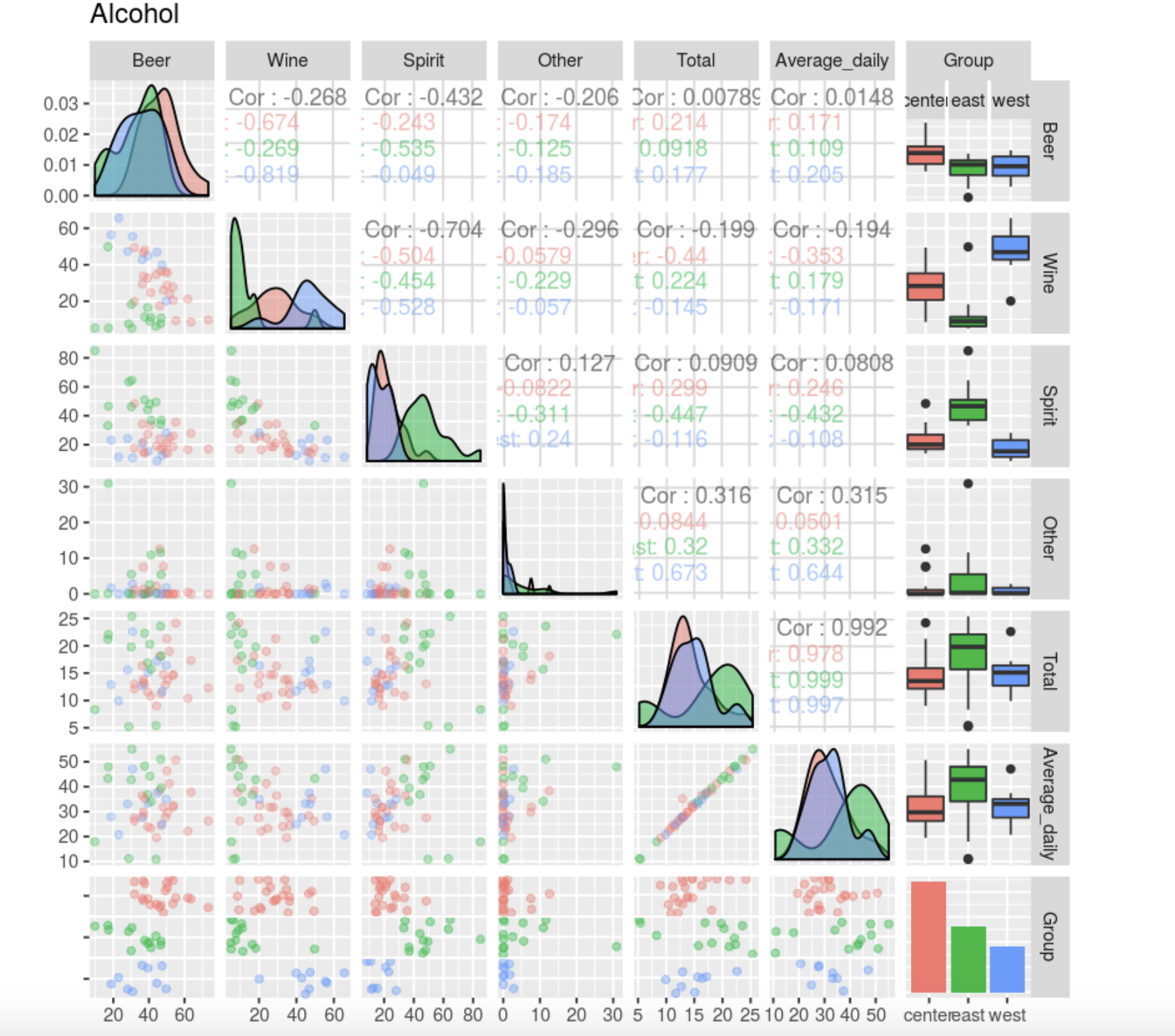
Average Total , Average.

data <- data[, -6]

, , , , . .

data[data$Wine>60,]

, , , , - , , .

data[data$Spirit>70,]
data[data$Spirit<10,]

, , .

,

split(data[,1:5],data$Group)

$center

$east

$west

ggpairs(
  data,
  mapping = ggplot2::aes(color = data$Group),
  diag=list(continuous="bar", alpha=0.4)
)

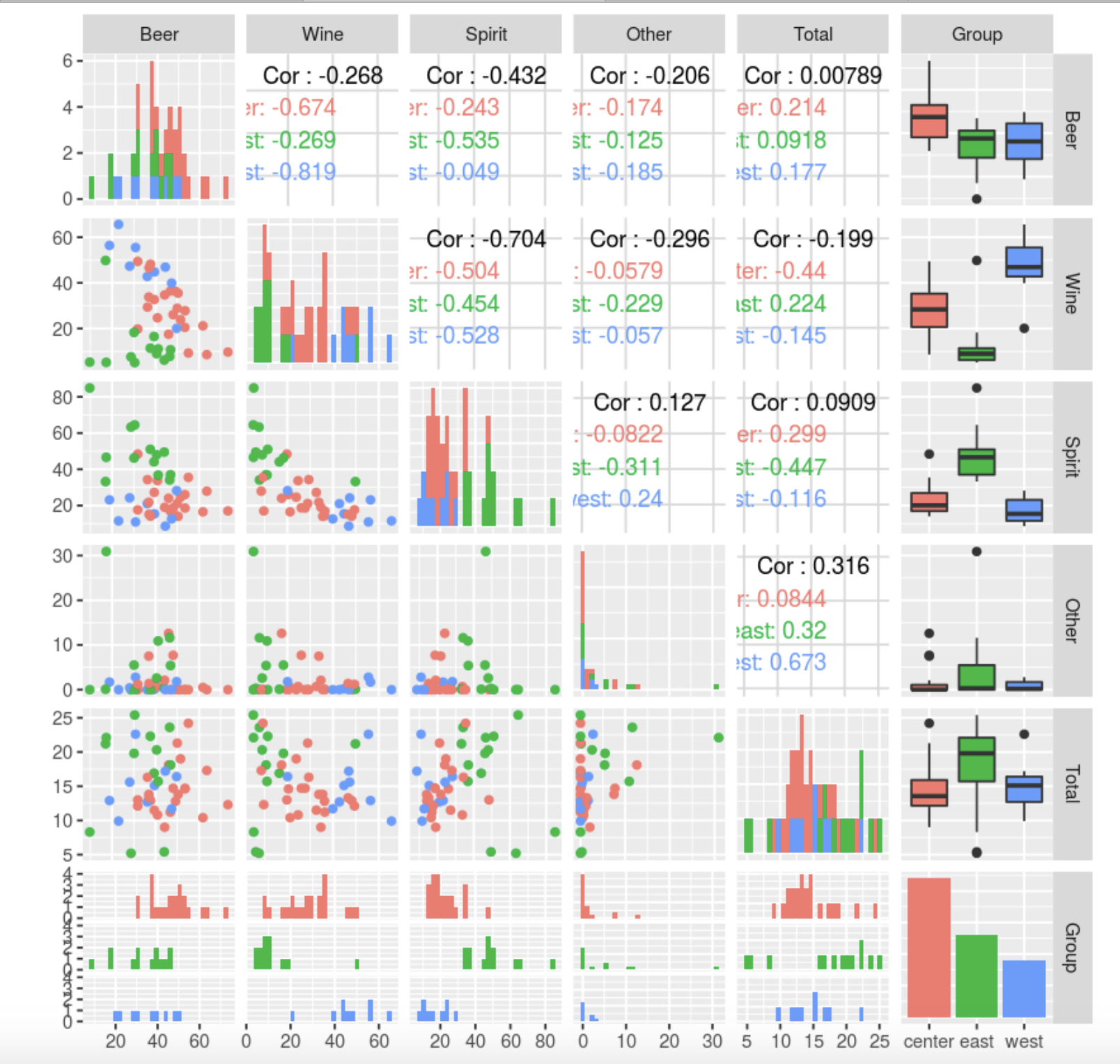
, , . Other, : , , , ( 10-12 , 45, , ). . , , , (). , , . Other .

, , — , — . , — , .
Total Other, . .

, Beer, Spirit Wine . , , , . , , , , , .

Total. , — .

data.group = data[,5]
data <- data[,-5]
data<- data[,-4]

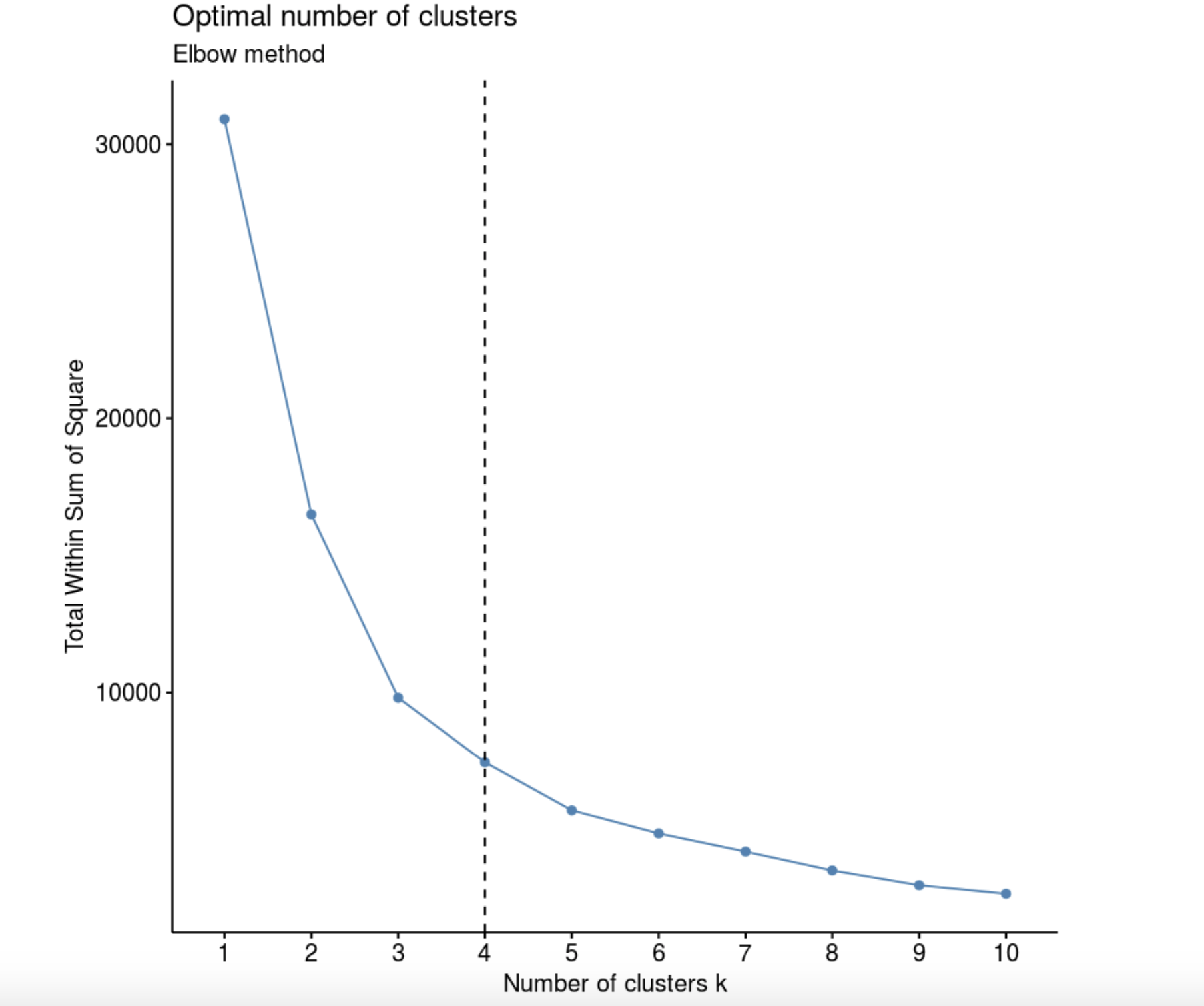
Elbow method (“ ”, “ ”). , k, – W(K), .

library(factoextra)
fviz_nbclust(data, kmeans, method = "wss") +
  labs(subtitle = "Elbow method") +
  geom_vline(xintercept = 4, linetype = 2)

data.dist <- dist((data))
hc <- hclust(data.dist, method = "ward.D2")
plot(hc, cex = 0.7)

. .

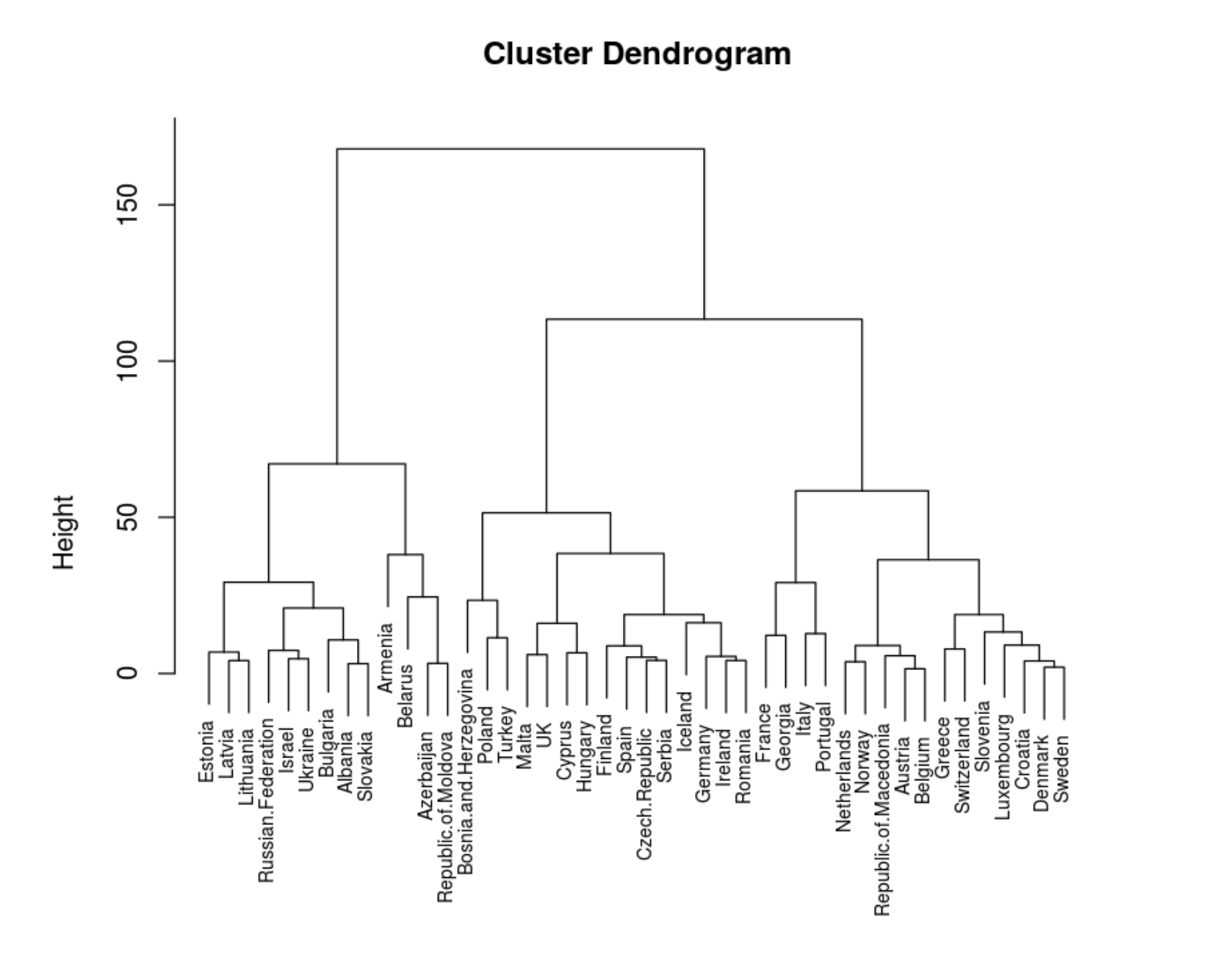
colors=c('green', 'red', 'blue')
hcd = as.dendrogram(hc)
clusMember = cutree(hc, 4)
colLab <- function(n) {
    if (is.leaf(n)) {
        a <- attributes(n)
        labCol <- colors[data.group[n]]
        attr(n, "nodePar") <- c(a$nodePar, lab.col = labCol)
    }
    n
}
clusDendro = dendrapply(hcd, colLab)
plot(clusDendro, main = "Cool Dendrogram", type = "triangle")

rect.hclust(hc, k = 4)

. , .
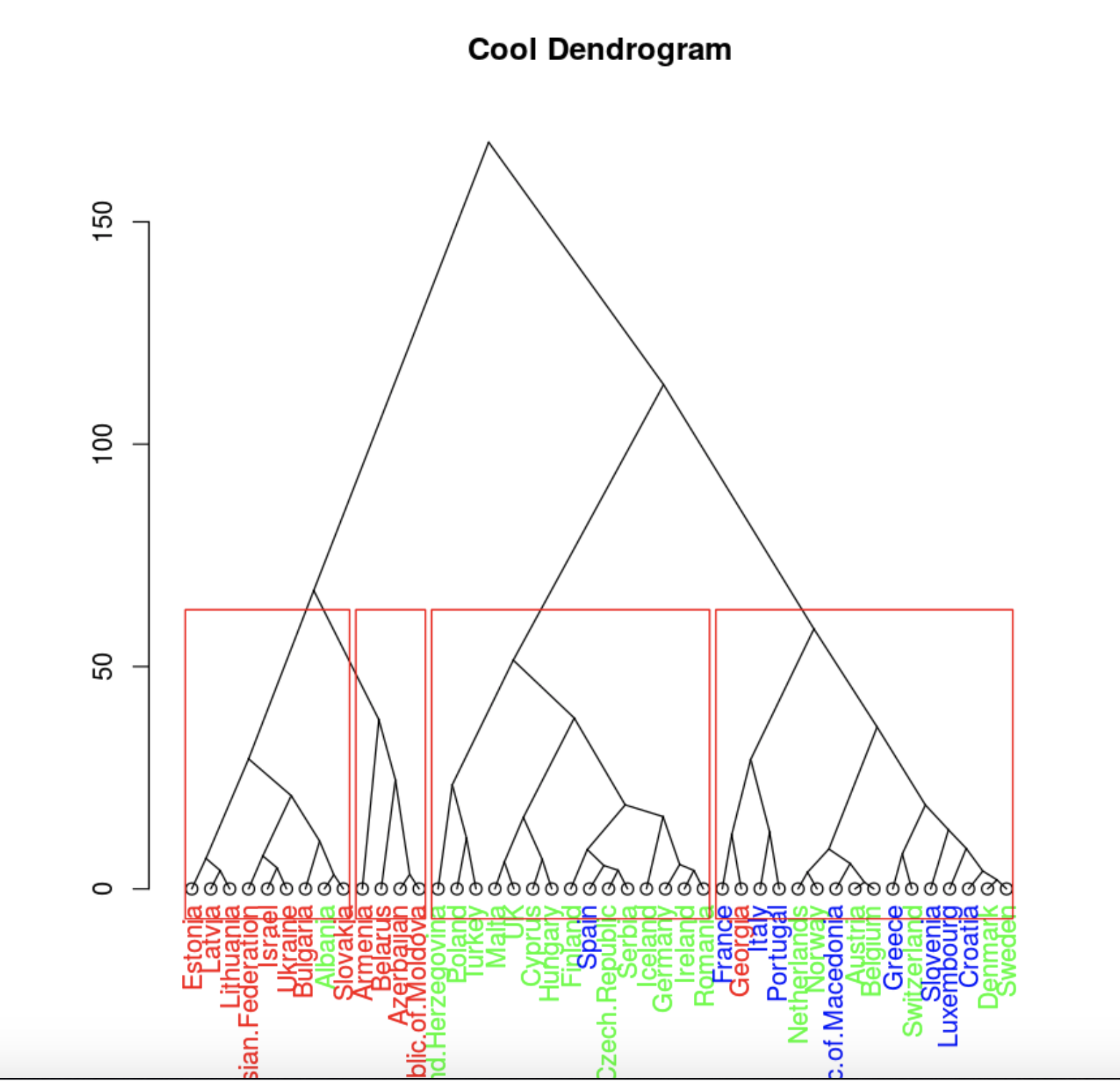
, , , 4 .

plot(clusDendro, main = "Cool Dendrogram", type = "triangle")
data.hclas_group <- factor(cutree(hc, k = 3))

rect.hclust(hc, k = 3)

, , .

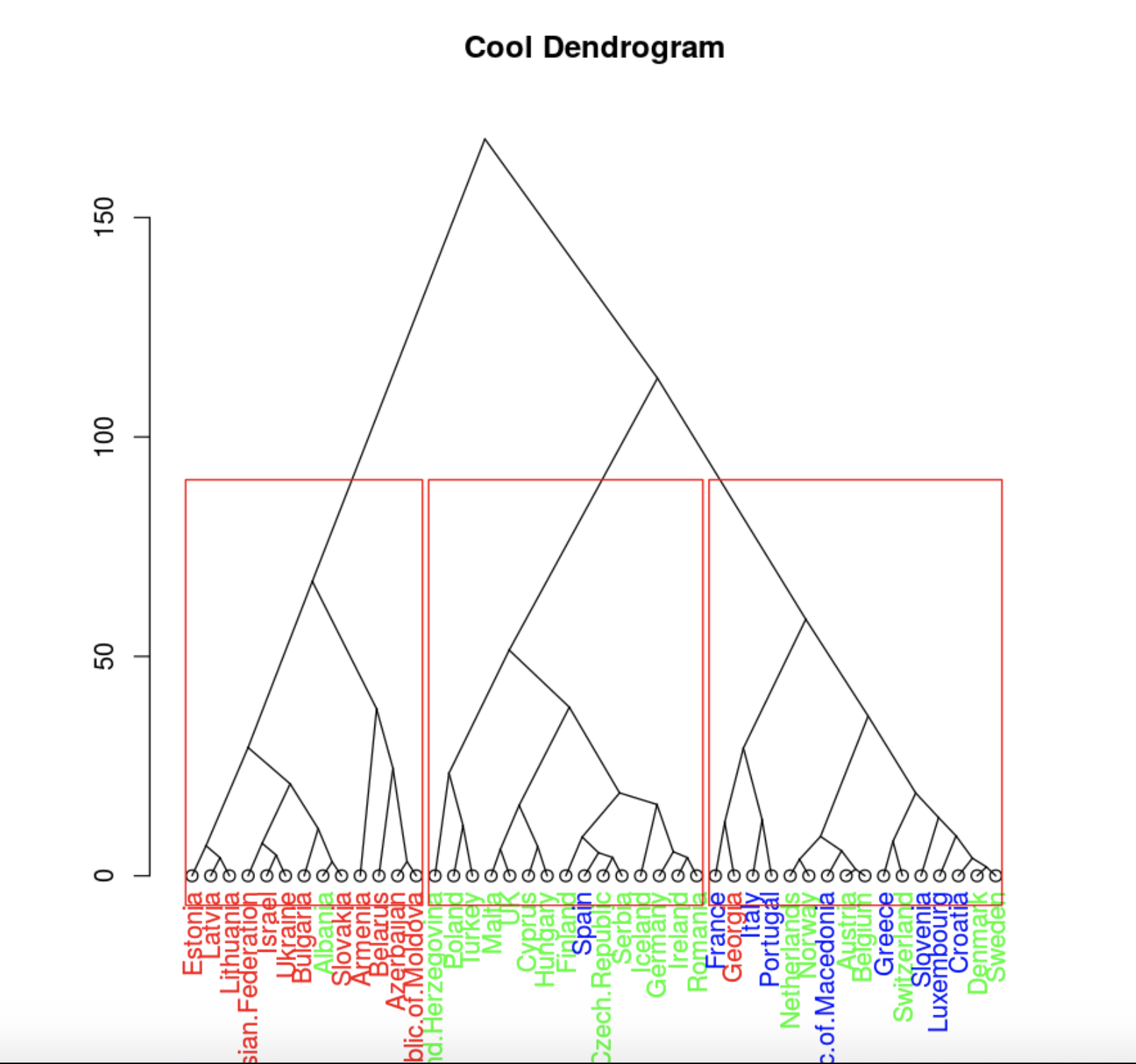
library(FactoMineR)
res.pca <- PCA(data,scale.unit=T, graph = F)
fviz_pca_biplot(res.pca, 
                col = colors[data.hclas_group], palette = "jco", 
                label = "var",
                ellipse.level = 0.8,
                 addEllipses = T,
                col.var = "black",
                legend.title = "groups4")

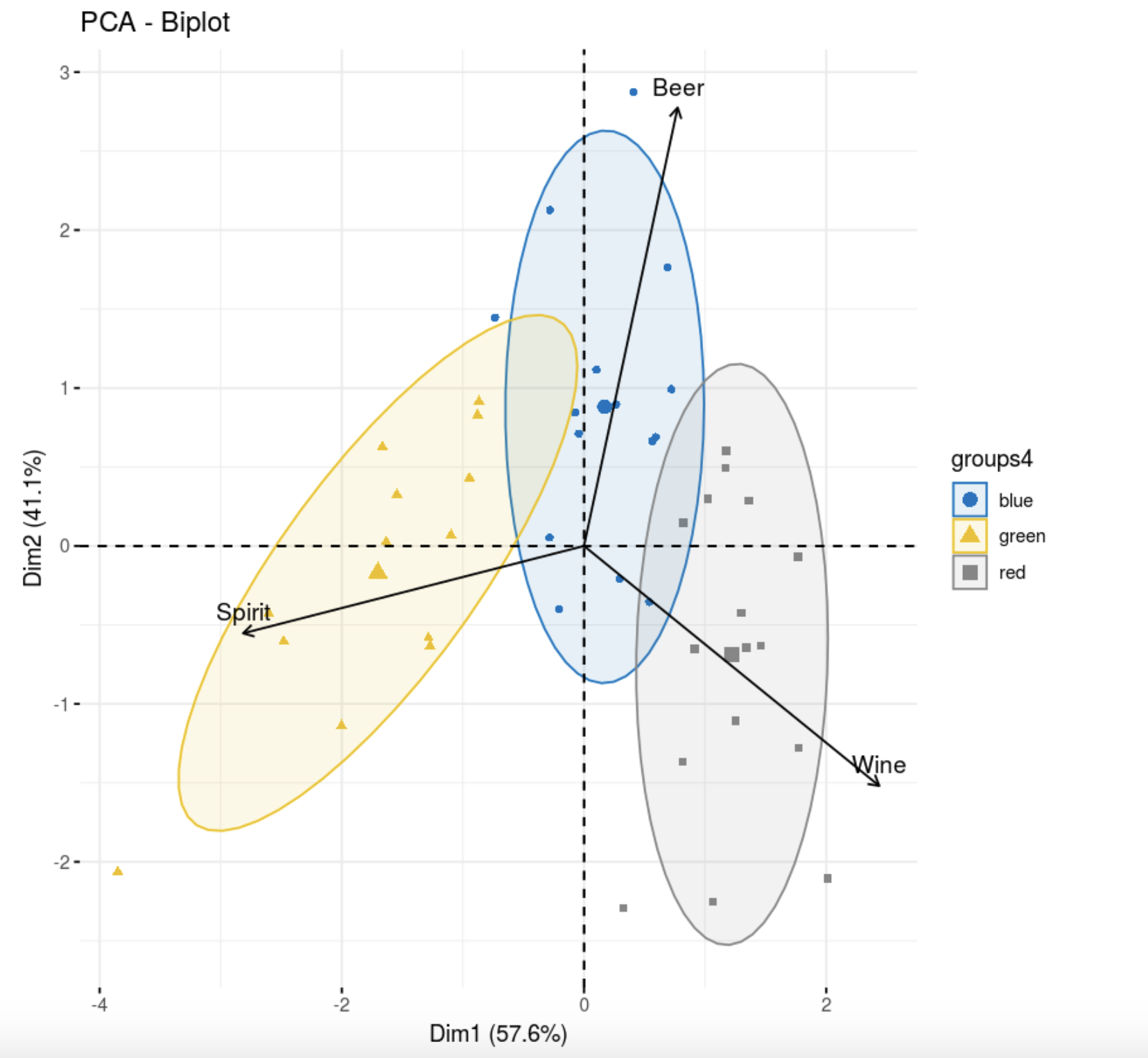
, , . , , , , . , , , k-++.

library(flexclust)
data.kk <- kcca(data, k=3, family=kccaFamily("kmeans"),
control=list(initcent="kmeanspp"))

fviz_pca_biplot(res.pca, 
                col.ind =as.factor(data.kk@cluster), palette = "jco", 
                label = "var",
                ellipse.level = 0.8,
                 addEllipses = T,
                col.var = "black", repel = TRUE,
                legend.title = "clusters")

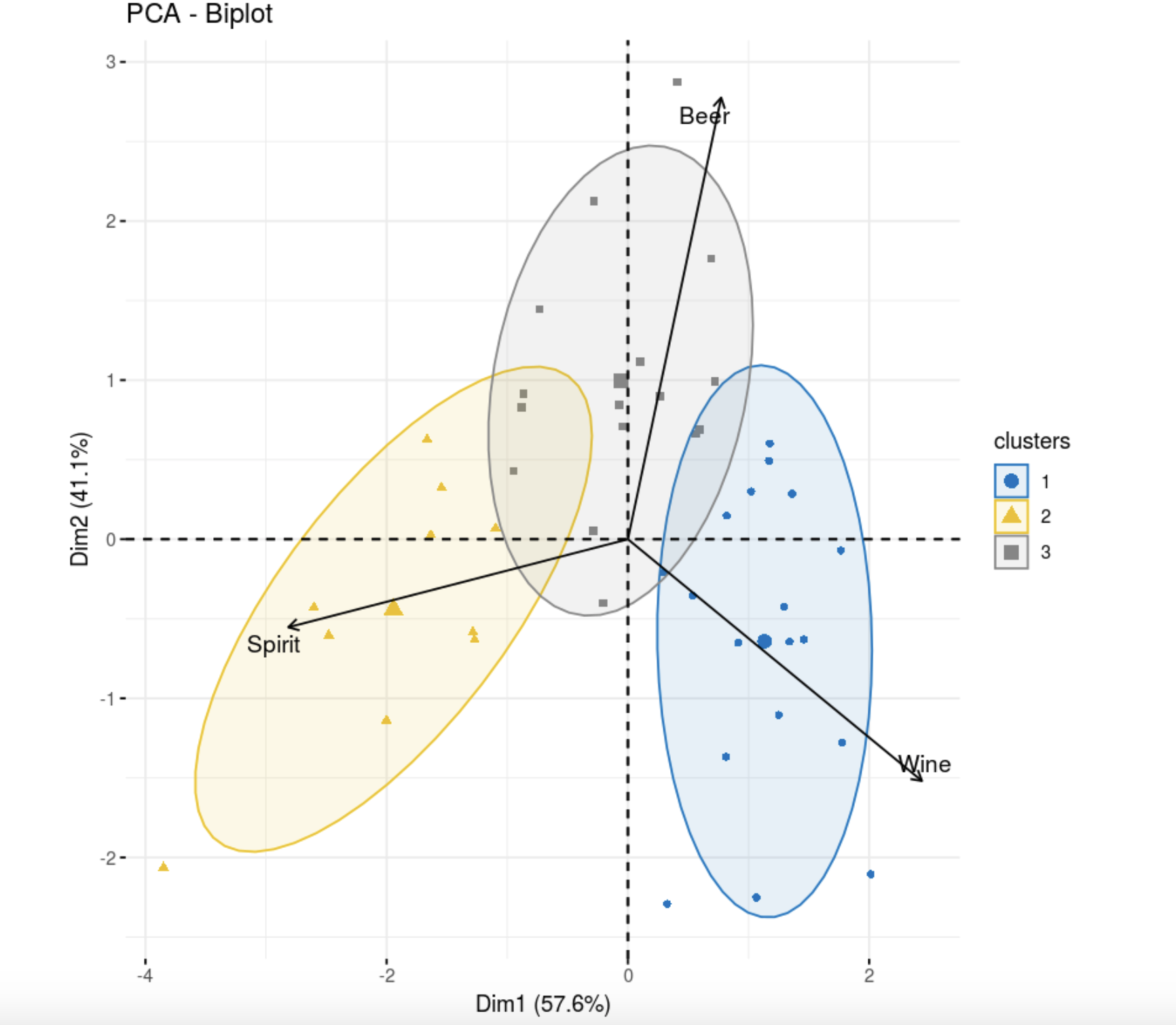
, k- . , , .

, , hclust. .

, , . . , .

. . , , , . , , . , .

Es wäre möglich, ein Clustering basierend auf der Annahme von Clustermodellen unter Verwendung von Informationskriterien durchzuführen ( hier die Beschreibung ) sowie die klassische Diskriminanzanalyse für diesen Datensatz zu versuchen. Wenn dieser Artikel nützlich war, plane ich, eine Fortsetzung zu veröffentlichen.