Guilloche ist ein charakteristisches Muster für Papiergeld und andere Wertpapiere. Eine ausführliche Geschichte über sie mit einem Exkurs in die Geschichte finden Sie im vorherigen Artikel . Dort wurde auch ein Zeichenalgorithmus angegeben, der Guillochen nach Punkten erstellt.Ziemlich nutzlos, sollte angemerkt werden, wenn wir sie nicht nur zum Spaß, sondern auch aus praktischen Gründen zeichnen - zum Beispiel, um dem Design genau diese Sicherheiten hinzuzufügen. Tausende von Punkten werden den Editor nur verlangsamen, aber er kann das Ergebnis trotzdem nicht anzeigen - anstelle von echten durchgehenden Linien wird es eine Art Ergebnis der Mittelung der Punkte geben, die so gemacht wurden, als würde Gott eine Seele aufsetzen.Daher ist es an der Zeit, über einen anderen Algorithmus nachzudenken, der sofort Vektoren liefert. Da die gängigen Editoren für gekrümmte Linien nur die Interpolation durch Bezier-Kurven anbieten, werden wir uns auf diese konzentrieren.Der Algorithmus ist in der Tat einfach - und viel einfacher als im ersten Teil beschrieben. Wir nehmen zwei Hüllkurven, legen die Anzahl der Wellen fest, die in 360 Grad passen sollen, schätzen, in welchem Winkel und mit welcher Krümmung die echte Guilloche vom aktuellen Punkt zum nächsten gehen soll, und interpolieren sie mit vier Bezier-Kurven.Hier ist ein Programm in Asymptote, das für solche Dinge äußerst praktisch ist.import graph;
size(1000,1000);
xaxis(ticks=Ticks);
yaxis(ticks=Ticks);
defaultpen(2);
var zero = (0,0);
real tens(bool at_top, real angle)
{
return angle/180;
}
guide wave(path top, path bottom, int parts, real offset)
{
guide w;
real step = 1/parts;
real half = step/2;
pair[] top_pt;
pair[] bot_pt;
pair[] top_dir;
pair[] bot_dir;
real[] top_angle;
real[] bot_angle;
for(int i: sequence(0,parts-1))
{
real rel = i*step + step*offset;
real top_time = reltime(top, rel);
real bot_time = reltime(bottom, rel+half);
top_pt[i] = point(top, top_time);
bot_pt[i] = point(bottom, bot_time);
top_dir[i] = dir(top, top_time);
bot_dir[i] = dir(bottom, bot_time);
}
for(int i: sequence(0,parts-1))
{
int prev = i == 0 ? parts-1 : i-1;
int next = i == parts-1 ? 0 : i+1;
var v1 = bot_pt[i] - top_pt[i];
var v2 = bot_pt[prev] - top_pt[i];
var a = degrees(v2) - degrees(v1);
top_angle[i] = a<0 ? 360+a : a;
v1 = top_pt[i] - bot_pt[i];
v2 = top_pt[next] - bot_pt[i];
a = degrees(v2) - degrees(v1);
bot_angle[i] = a<0 ? 360+a : a;
}
for(int i: sequence(0,parts-1))
{
int next = i == parts-1 ? 0 : i+1;
var l1 = length(top_pt[i]--bot_pt[i]);
pair ctl1 = top_pt[i] + top_dir[i] * tens(true, top_angle[i]) * l1;
pair ctl2 = bot_pt[i] - bot_dir[i] * tens(false, bot_angle[i]) * l1;
w = w .. top_pt[i] .. controls ctl1 and ctl2 .. bot_pt[i];
var l2 = length(bot_pt[i]--top_pt[next]);
ctl1 = bot_pt[i] + bot_dir[i] * tens(false, bot_angle[i]) * l2;
ctl2 = top_pt[next] - top_dir[next] * tens(true, top_angle[next]) * l2;
w = w .. bot_pt[i] .. controls ctl1 and ctl2 .. top_pt[next];
}
return w;
}
void repeat(int count, path top, path bottom, int parts)
{
real step = 1/count;
for(int i: sequence(0, count-1))
{
draw(wave(top, bottom, parts, step*i));
}
}
path normalize(path p)
{
var min = min(p);
var max = max(p);
var top_center = min + ((max.x-min.x)/2, (max.y-min.y)/2);
return scale(20*1/(max-min).x)*shift(zero - top_center)*p;
}
path top = (338.499521684,-159.274266483)
..controls (327.252951684,-158.148796483) and (323.448961684,-145.618286483) .. (318.743661684,-137.260595483)
..controls (309.897671684,-123.808725483) and (292.025851684,-123.657732483) .. (278.251471684,-118.807470483)
..controls (272.669581684,-117.510629483) and (268.731931684,-109.221757483) .. (274.571781684,-105.645360483)
..controls (281.545351684,-101.031122483) and (290.488261684,-97.7906864833) .. (293.317871684,-89.0437964838)
..controls (296.611021684,-81.8498064838) and (293.894071684,-73.5853264838) .. (295.556161684,-66.3445764838)
..controls (299.563831684,-59.7686064838) and (308.181311684,-64.5344964838) .. (312.903811684,-67.4344264838)
..controls (325.368171684,-74.9872364838) and (341.157891684,-80.6126364838) .. (355.257331684,-73.9383264838)
..controls (363.506651684,-70.9246164838) and (370.115991684,-63.9703964838) .. (378.731941684,-62.0926264838)
..controls (384.688491684,-61.4010364838) and (389.980631684,-67.6129964838) .. (387.306161684,-73.3211464838)
..controls (385.256921684,-82.8346964838) and (388.441441684,-93.9447564833) .. (397.757331684,-98.3016064833)
..controls (403.144721684,-101.085582483) and (412.671611684,-104.606352483) .. (410.331551684,-112.414892483)
..controls (406.654931684,-119.718595483) and (396.921641684,-119.937732483) .. (390.144051684,-122.524267483)
..controls (378.065751684,-125.483516483) and (364.313841684,-130.717262483) .. (359.884541684,-143.562216483)
..controls (356.731021684,-151.157386483) and (350.818391684,-160.192046483) .. (341.435061684,-159.293796483)
..controls (340.456461684,-159.306096483) and (339.478031684,-159.281196483) .. (338.499521684,-159.274296483)
--cycle;
top = normalize(top);
bottom = scale(0.5)*top;
top = ellipse(zero, 4, 6);
bottom = ellipse(zero, 2, 3);
top = circle(zero, 5);
bottom = circle(zero, 3);
repeat(12, top, bottom, 8);
Der verständlichste Fall ist, wenn sich die Sinuskurven zwischen zwei Kreisen befinden.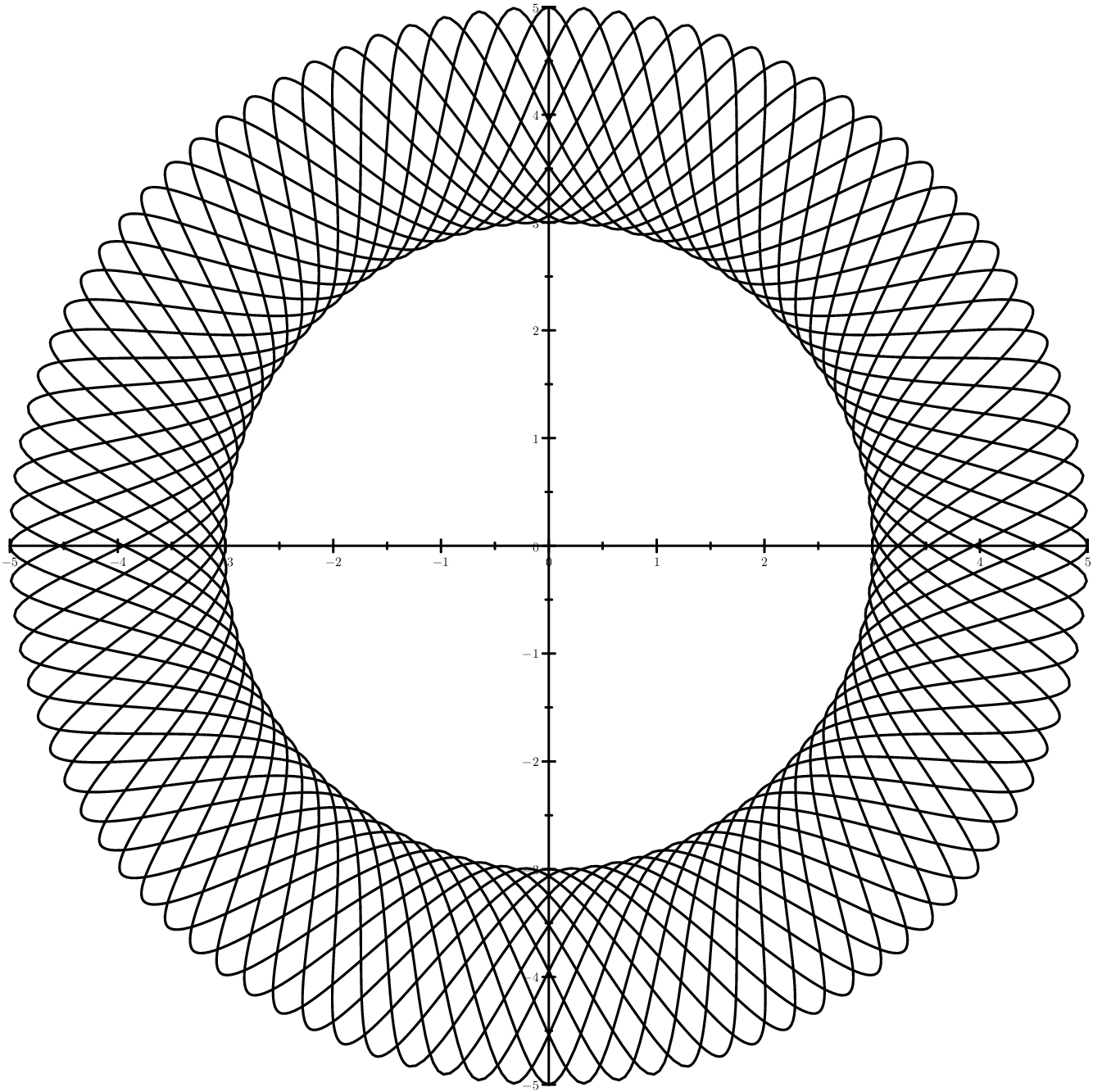
Der Fall ist schlauer - Ellipsen statt Kreise.
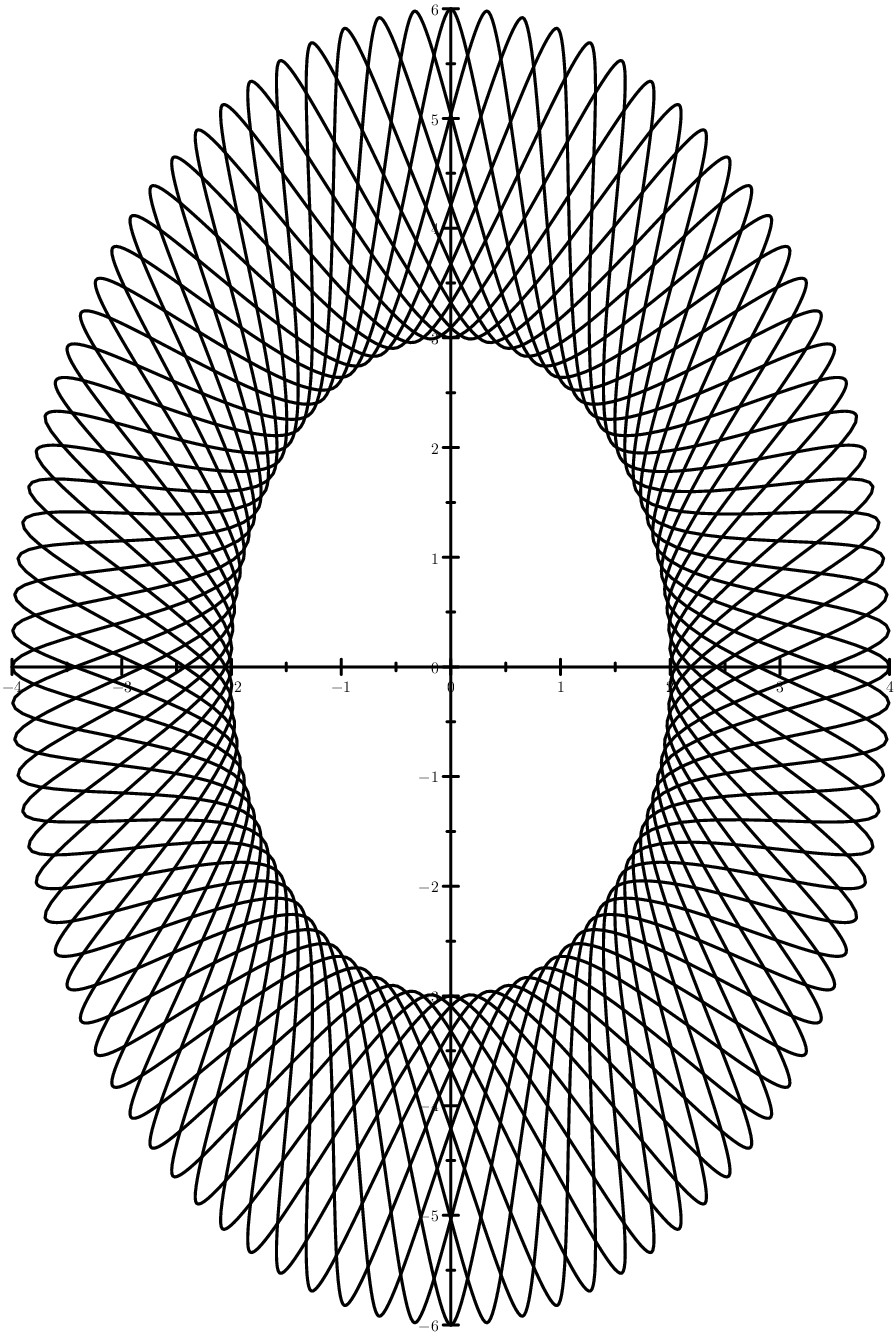Und ein Bild, das der industriellen Nutzung nahe kommt: Guilloche, eine Art künstlerisches Medium.
Hier ist das Ergebnis jedoch nicht perfekt. Zunächst musste die Zehnerfunktion so eingestellt werden, dass immer eine konstante „Spannung“ von 0,5 zurückgegeben wurde. Und zweitens sind die Kurven nicht sehr symmetrisch und im linken Teil nahe der X-Achse irgendwie verwirrt. Natürlich kann all dies von Hand korrigiert werden, insbesondere wenn Sie Banknoten für den Staat erstellen und sehr qualifizierte Künstler haben, aber Sie können versuchen, die Genauigkeit der Berechnungen zu erhöhen, da diese offensichtlich an einigen Stellen in die Irre gehen, an denen sich die Krümmung der Hüllkurve stark ändert.Da die Guillochen interpoliert sind, stellt sich die Frage: Stimmen sie sozusagen mit „real“ überein, dh durch Punkte gezeichnet. Da ich neu in der Differentialgeometrie bin, fällt es mir schwer zu sagen, aber eher "Nein" als "Ja".Aber wer sieht den Unterschied wirklich?Der praktische Vorteil ist unbestreitbar: Mit ein paar Dutzend Bezier-Kurven ist das Arbeiten viel einfacher als mit tausend Punkten, und sie eröffnen viel mehr Gestaltungsmöglichkeiten.Darüber hinaus kann dieser Algorithmus auch verbessert werden. Zwei Optionen bieten sich sofort an:a) Geben Sie eine unterschiedliche Anzahl von Punkten auf der externen und internen Kurve an. Dann wird der Effekt des Schleifens des Musters näher an der Mitte nicht erzeugt, wie in den Beispielen mit einem Kreis und einer Ellipse.b) Platzieren Sie die Punkte nicht gleichmäßig auf den Umschlägen, sondern machen Sie sie beispielsweise häufiger und seltener, wodurch dem Muster eine neue Dimension hinzugefügt wird.