🐜 👂🏿 🥕 Worauf wir bei der Berechnung der statistischen Signifikanz des A / B-Tests achten ✒️ 🏂🏼 ▫️

In Uchi.ru versuchen wir, mit dem A / B-Test auch kleine Verbesserungen einzuführen. In diesem akademischen Jahr gab es mehr als 250 davon. Der A / B-Test ist ein leistungsstarkes Tool für Änderungstests, ohne das die normale Entwicklung eines Internetprodukts kaum vorstellbar ist. Gleichzeitig können trotz der offensichtlichen Einfachheit während des A / B-Tests sowohl in der Entwurfsphase des Experiments als auch bei der Zusammenfassung der Ergebnisse schwerwiegende Fehler gemacht werden. In diesem Artikel werde ich auf einige technische Aspekte des Tests eingehen: wie wir den Testzeitraum bestimmen, zusammenfassen und wie fehlerhafte Ergebnisse vermieden werden, wenn die Tests vorzeitig abgeschlossen werden und mehrere Hypothesen gleichzeitig getestet werden.

Ein typisches A / B-Testschema für uns (und für viele) sieht folgendermaßen aus:

Wir entwickeln ein Feature, aber bevor wir es für das gesamte Publikum bereitstellen, möchten wir sicherstellen, dass es die Zielmetrik verbessert, z. B. das Engagement.
Wir bestimmen den Zeitraum, für den der Test gestartet wird.
Wir teilen Benutzer zufällig in zwei Gruppen ein.
Wir zeigen einer Gruppe die Produktversion mit Funktionen (Versuchsgruppe), die andere - die alte (Kontrolle).
Dabei überwachen wir die Metrik, um einen besonders erfolglosen Test rechtzeitig zu stoppen.
Nach Ablauf des Tests vergleichen wir die Metrik in der Versuchsgruppe und der Kontrollgruppe.
Wenn die Metrik in der Versuchsgruppe statistisch signifikant besser ist als in der Kontrollgruppe, führen wir das getestete Merkmal überhaupt ein. Wenn keine statistische Signifikanz vorliegt, beenden wir den Test mit einem negativen Ergebnis.

Alles sieht logisch und einfach aus, der Teufel wie immer im Detail.

Statistische Signifikanz, Kriterien und Fehler

In jedem A / B-Test gibt es ein zufälliges Element: Gruppenmetriken hängen nicht nur von ihrer Funktionalität ab, sondern auch davon, was Benutzer in sie aufgenommen haben und wie sie sich verhalten. Um zuverlässig Schlussfolgerungen über die Überlegenheit einer Gruppe zu ziehen, müssen Sie im Test genügend Beobachtungen sammeln, aber selbst dann sind Sie nicht immun gegen Fehler. Sie unterscheiden sich durch zwei Arten:

Ein Fehler der ersten Art tritt auf, wenn wir den Unterschied zwischen den Gruppen beheben, obwohl er in Wirklichkeit nicht existiert. Der Text enthält auch einen äquivalenten Begriff - ein falsch positives Ergebnis. Der Artikel widmet sich genau solchen Fehlern.
Ein Fehler der zweiten Art tritt auf, wenn wir das Fehlen eines Unterschieds beheben, obwohl dies tatsächlich der Fall ist.

Bei einer Vielzahl von Experimenten ist es wichtig, dass die Wahrscheinlichkeit eines Fehlers der ersten Art gering ist. Es kann mit statistischen Methoden gesteuert werden. Zum Beispiel möchten wir, dass die Wahrscheinlichkeit eines Fehlers der ersten Art in jedem Experiment 5% nicht überschreitet (dies ist nur ein praktischer Wert, Sie können einen anderen für Ihre eigenen Bedürfnisse nehmen). Dann werden wir Experimente mit einem Signifikanzniveau von 0,05 durchführen:

Es gibt einen A / B-Test mit Kontrollgruppe A und Versuchsgruppe B. Ziel ist es zu überprüfen, ob sich Gruppe B in einigen Metriken von Gruppe A unterscheidet.
Wir formulieren die statistische Nullhypothese: Die Gruppen A und B unterscheiden sich nicht, und die beobachteten Unterschiede werden durch Rauschen erklärt. Standardmäßig denken wir immer, dass es keinen Unterschied gibt, bis das Gegenteil bewiesen ist.
Wir überprüfen die Hypothese mit einer strengen mathematischen Regel - einem statistischen Kriterium, zum Beispiel dem Kriterium des Schülers.
Als Ergebnis erhalten wir den p-Wert. Sie liegt im Bereich von 0 bis 1 und bedeutet die Wahrscheinlichkeit, den aktuellen oder extremeren Unterschied zwischen Gruppen zu sehen, vorausgesetzt, die Nullhypothese ist wahr, dh wenn kein Unterschied zwischen den Gruppen besteht.
Der p-Wert wird mit einem Signifikanzniveau von 0,05 verglichen. Wenn es größer ist, akzeptieren wir die Nullhypothese, dass es keine Unterschiede gibt, andernfalls glauben wir, dass es einen statistisch signifikanten Unterschied zwischen den Gruppen gibt.

Eine Hypothese kann mit einem parametrischen oder nichtparametrischen Kriterium getestet werden. Die parametrischen Werte stützen sich auf die Parameter der Stichprobenverteilung einer Zufallsvariablen und haben mehr Leistung (sie machen seltener Fehler der zweiten Art), stellen jedoch Anforderungen an die Verteilung der untersuchten Zufallsvariablen.

Der häufigste parametrische Test ist der Studententest. Für zwei unabhängige Stichproben (A / B-Testfall) wird es manchmal als Welch-Kriterium bezeichnet. Dieses Kriterium funktioniert korrekt, wenn die untersuchten Mengen normal verteilt sind. Es mag den Anschein haben, dass diese Anforderung bei realen Daten fast nie erfüllt wird, aber tatsächlich erfordert der Test eine Normalverteilung der Stichprobenmittelwerte, nicht der Stichproben selbst. In der Praxis bedeutet dies, dass das Kriterium angewendet werden kann, wenn Sie in Ihrem Test viele Beobachtungen haben (zehn bis hundert) und die Verteilungen keine sehr langen Schwänze enthalten. Die Art der Verteilung der ersten Beobachtungen ist unwichtig. Der Leser kann unabhängig überprüfen, ob das Student-Kriterium auch bei Proben, die aus Bernoulli oder Exponentialverteilungen generiert wurden, korrekt funktioniert.

Unter den nichtparametrischen Kriterien ist das Mann-Whitney-Kriterium beliebt. Es sollte verwendet werden, wenn Ihre Proben sehr klein sind oder große Ausreißer aufweisen (die Methode vergleicht die Mediane, ist daher resistent gegen Ausreißer). Damit das Kriterium korrekt funktioniert, sollten die Stichproben nur wenige übereinstimmende Werte aufweisen. In der Praxis mussten wir nie nichtparametrische Kriterien anwenden, in unseren Tests verwenden wir immer das Schülerkriterium.

Das Problem des Testens mehrerer Hypothesen

Das offensichtlichste und einfachste Problem: Wenn es im Test zusätzlich zur Kontrollgruppe mehrere experimentelle gibt, führt die Zusammenfassung der Ergebnisse mit einem Signifikanzniveau von 0,05 zu einer mehrfachen Erhöhung des Fehleranteils der ersten Art. Dies liegt daran, dass bei jeder Anwendung des statistischen Kriteriums die Wahrscheinlichkeit eines Fehlers der ersten Art 5% beträgt. Mit der Anzahl der Gruppen

n g r o u p s

$ngroups$ und Signifikanzniveau

α

$\alpha$ Die Wahrscheinlichkeit, dass eine Versuchsgruppe zufällig gewinnt, ist:

P (a n y f a l s e p o s i t i v e) = 1 - (1 - α)^{n g r o u p s}

$P(any\ false\ positive) = 1 − (1 − \alpha) ^ {ngroups}$

Zum Beispiel erhalten wir für die drei Versuchsgruppen 14,3% anstelle der erwarteten 5%. Das Problem wird durch Bonferronis Korrektur für das Testen mehrerer Hypothesen gelöst: Sie müssen nur das Signifikanzniveau durch die Anzahl der Vergleiche (d. H. Gruppen) dividieren und damit arbeiten. Für das obige Beispiel beträgt das Signifikanzniveau unter Berücksichtigung der Änderung 0,05 / 3 = 0,0167, und die Wahrscheinlichkeit, dass mindestens ein Fehler der ersten Art vorliegt, beträgt 4,9%.

Hill-Methode - Bonferroni

— , , , .

n g r o u p s

$ngroups$ p-value ,

s t e p_n u m b e r

$step\_number$ :

α_{s t e p} = \frac{α}{n g r o u p s - s t e p_n u m b e r + 1}

$\alpha_{step} = \frac {\alpha} {ngroups − step\_number + 1}$

P-value

α / n g r o u p s

$\alpha/ngroups$ . , p-value

α / (n g r o u p s - 1)

$\alpha/(ngroups − 1)$ , . - , . ( , ) p-value, . A/B- — , — .

Genau genommen unterliegen Vergleiche von Gruppen nach verschiedenen Metriken oder Teilen des Publikums auch dem Problem mehrerer Tests. Formal ist es ziemlich schwierig, alle Überprüfungen zu berücksichtigen, da ihre Anzahl im Voraus schwer vorherzusagen ist und sie manchmal nicht unabhängig sind (insbesondere wenn es um unterschiedliche Metriken geht, nicht um Slices). Es gibt kein universelles Rezept. Verlassen Sie sich auf den gesunden Menschenverstand und denken Sie daran, dass Sie bei jedem Test ein statistisch signifikantes Ergebnis sehen können, wenn Sie viele Slices mit unterschiedlichen Metriken überprüfen. So sollte man zum Beispiel darauf achten, dass die Bindung neuer mobiler Nutzer aus Großstädten am fünften Tag deutlich zunimmt.

Peeping Problem

Ein besonderer Fall des Testens mehrerer Hypothesen ist das Peeking-Problem. Der Punkt ist, dass der p-Wert während des Tests versehentlich unter das akzeptierte Signifikanzniveau fallen kann. Wenn Sie das Experiment sorgfältig überwachen, können Sie diesen Moment erfassen und einen Fehler in Bezug auf die statistische Signifikanz machen.

Angenommen, wir haben uns von dem zu Beginn des Beitrags beschriebenen Testaufbau entfernt und beschlossen, jeden Tag (oder nur mehrmals während des Tests) eine Bestandsaufnahme mit einem Signifikanzniveau von 5% vorzunehmen. Zusammenfassend verstehe ich, dass der Test positiv ist, wenn der p-Wert unter 0,05 liegt, und seine Fortsetzung ansonsten. Mit dieser Strategie wird der Anteil falsch positiver Ergebnisse proportional zur Anzahl der Kontrollen sein und im ersten Monat 28% erreichen. Ein solch großer Unterschied scheint nicht intuitiv zu sein, daher wenden wir uns der Methodik der A / A-Tests zu, die für die Entwicklung von A / B-Testschemata unverzichtbar ist.

Die Idee eines A / A-Tests ist einfach: Viele A / B-Tests mit zufälligen Daten mit zufälliger Gruppierung zu simulieren. Es gibt offensichtlich keinen Unterschied zwischen den Gruppen, sodass Sie den Anteil der Fehler der ersten Art in Ihrem A / B-Testschema genau abschätzen können. Das folgende GIF zeigt, wie sich der p-Wert für vier solcher Tests pro Tag ändert. Ein gleiches Signifikanzniveau von 0,05 wird durch eine gestrichelte Linie angezeigt. Wenn der p-Wert unterschreitet, färben wir das Testdiagramm rot. Wenn zu diesem Zeitpunkt die Testergebnisse zusammengefasst würden, würde dies als erfolgreich angesehen.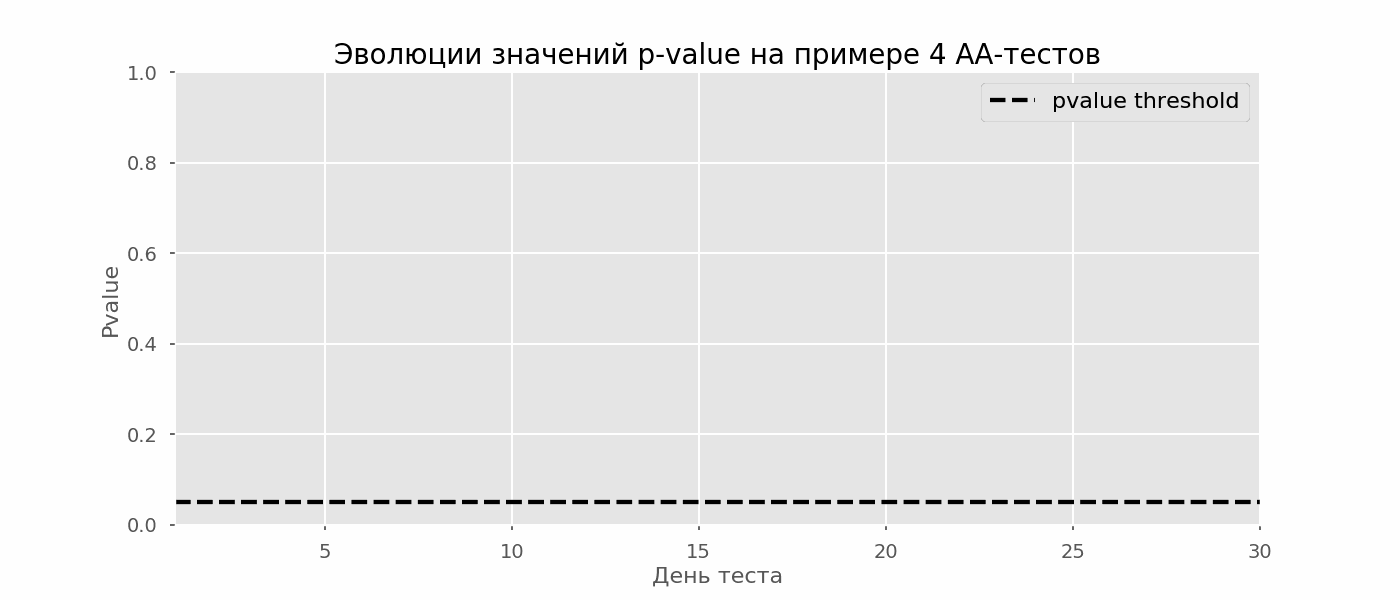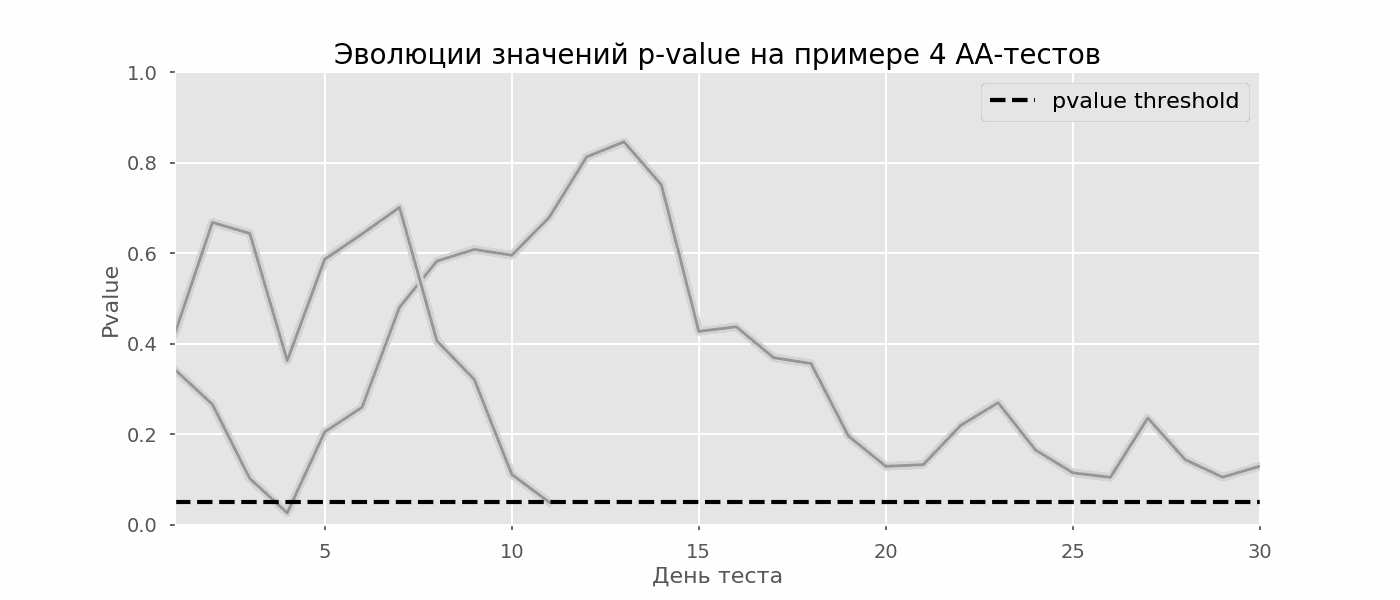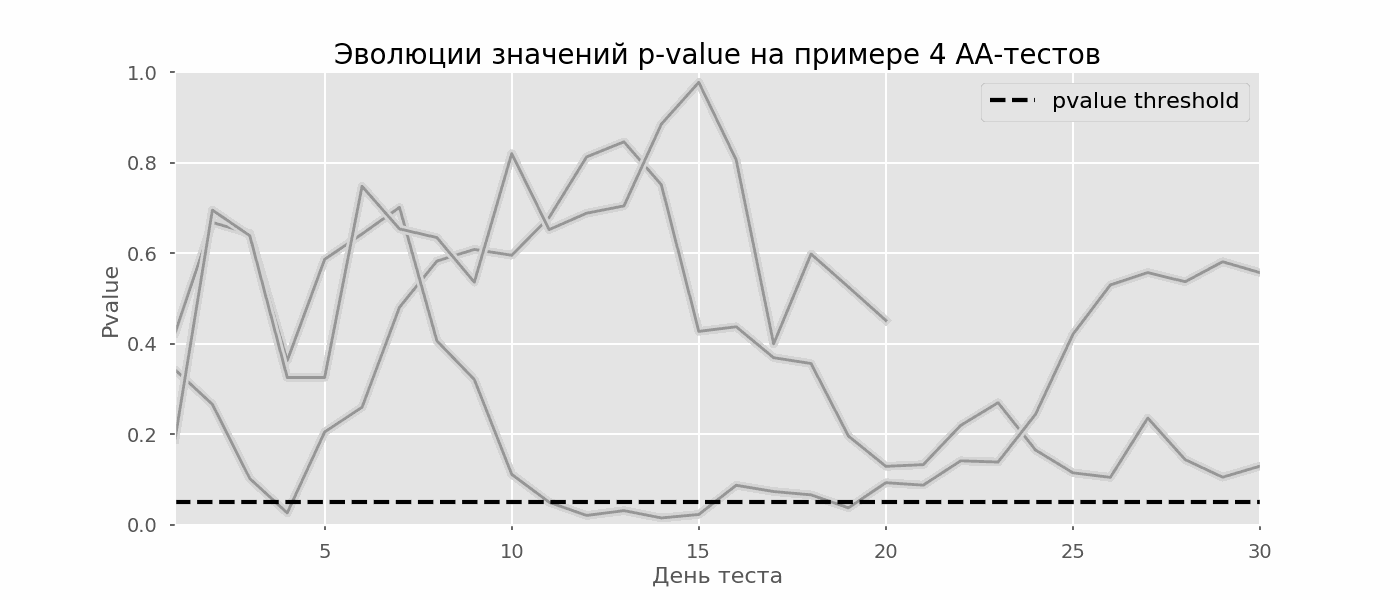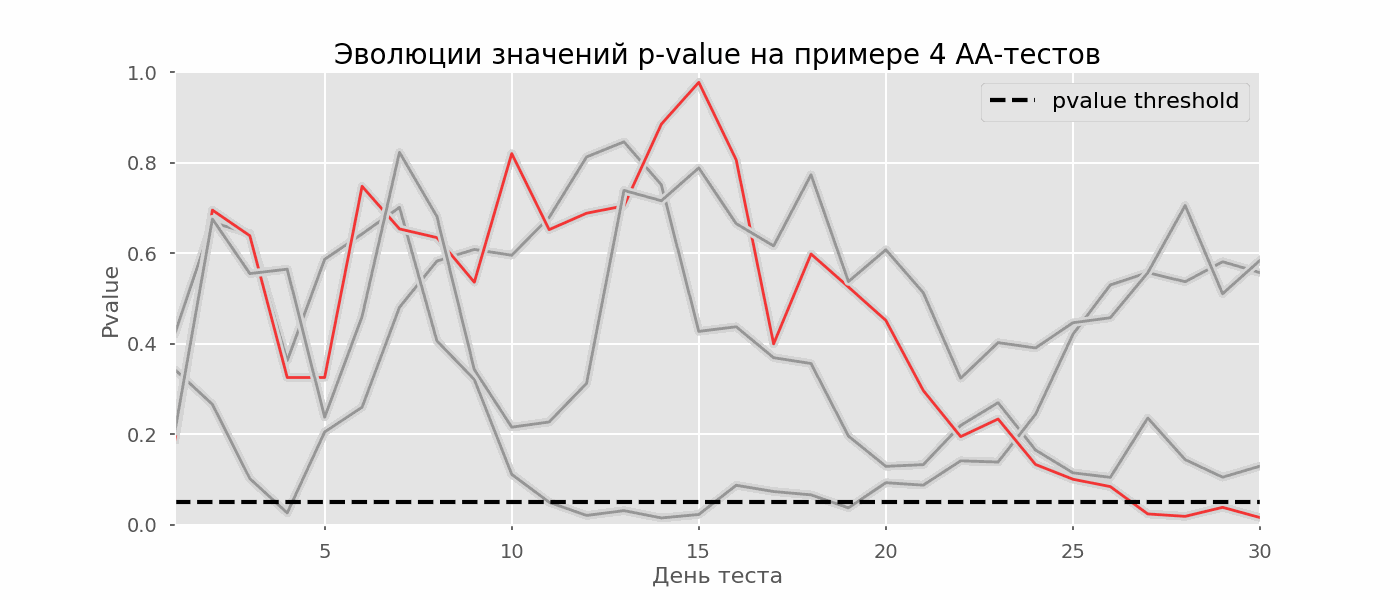

In ähnlicher Weise berechnen wir 10 000 A / A-Tests, die einen Monat dauern, und vergleichen die Anteile falsch positiver Ergebnisse im Schema mit der Zusammenfassung am Ende des Semesters und jeden Tag. Zur Verdeutlichung sind hier die p-Wert-Wanderungspläne pro Tag für die ersten 100 Simulationen aufgeführt. Jede Linie ist der p-Wert eines Tests. Die Trajektorien der Tests sind rot hervorgehoben. Diese werden fälschlicherweise als erfolgreich angesehen (je weniger, desto besser). Die gestrichelte Linie ist der erforderliche p-Wert, um den Test als erfolgreich zu erkennen.

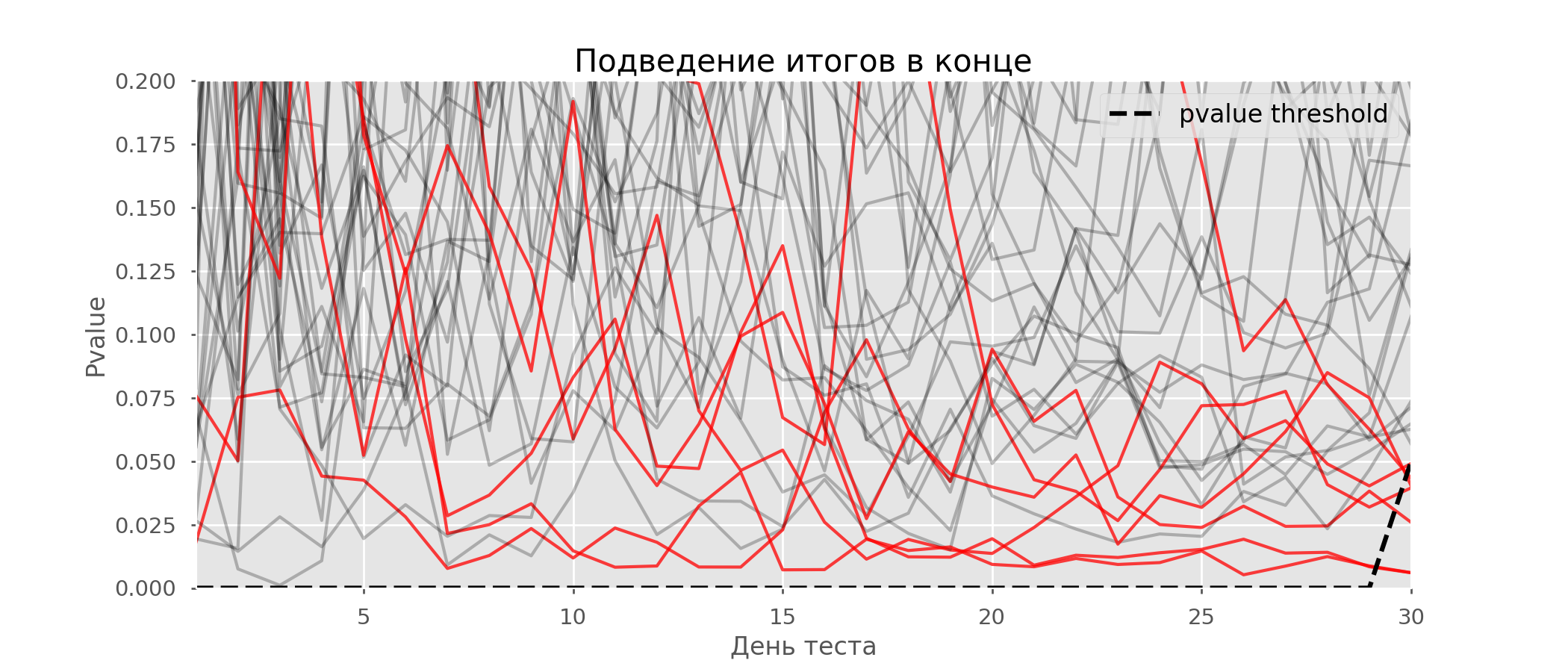In der Grafik können Sie 7 falsch positive Tests zählen, und insgesamt gab es unter 10 Tausend 502 oder 5%. Es ist anzumerken, dass der p-Wert vieler Tests im Verlauf der Beobachtungen unter 0,05 fiel, aber am Ende der Beobachtungen über das Signifikanzniveau hinausging. Lassen Sie uns nun das Testschema jeden Tag mit einer Nachbesprechung bewerten:

Es gibt so viele rote Linien, dass nichts klar ist. Wir werden neu zeichnen, indem wir die Testlinien durchbrechen, sobald ihr p-Wert einen kritischen Wert erreicht: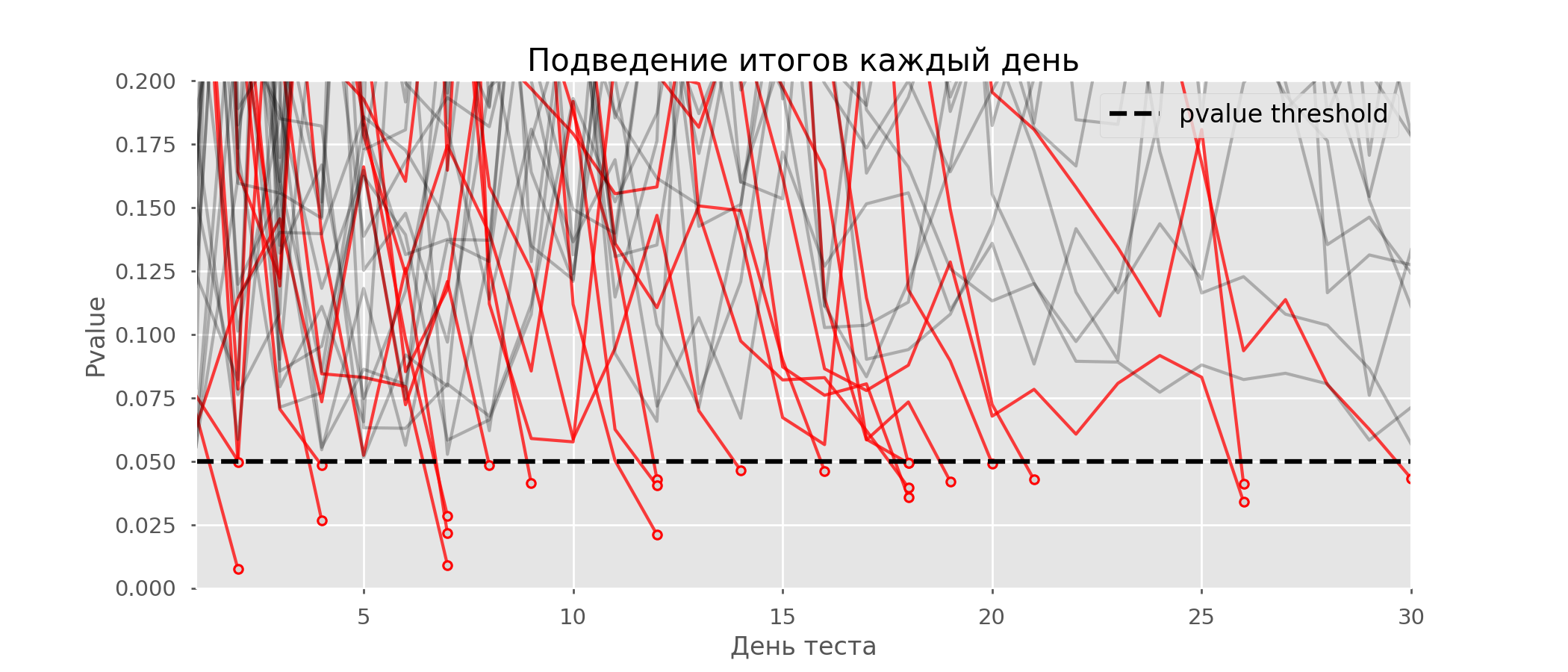

Es werden insgesamt 2813 falsch positive Tests von 10 Tausend oder 28% durchgeführt. Es ist klar, dass ein solches System nicht realisierbar ist.

Obwohl das Problem des Guckens ein Sonderfall mehrerer Tests ist, lohnt es sich nicht, Standardkorrekturen (Bonferroni und andere) anzuwenden, da sie sich als übermäßig konservativ herausstellen. Die folgende Grafik zeigt den Prozentsatz der falsch positiven Ergebnisse in Abhängigkeit von der Anzahl der getesteten Gruppen (rote Linie) und der Anzahl der Peeps (grüne Linie).

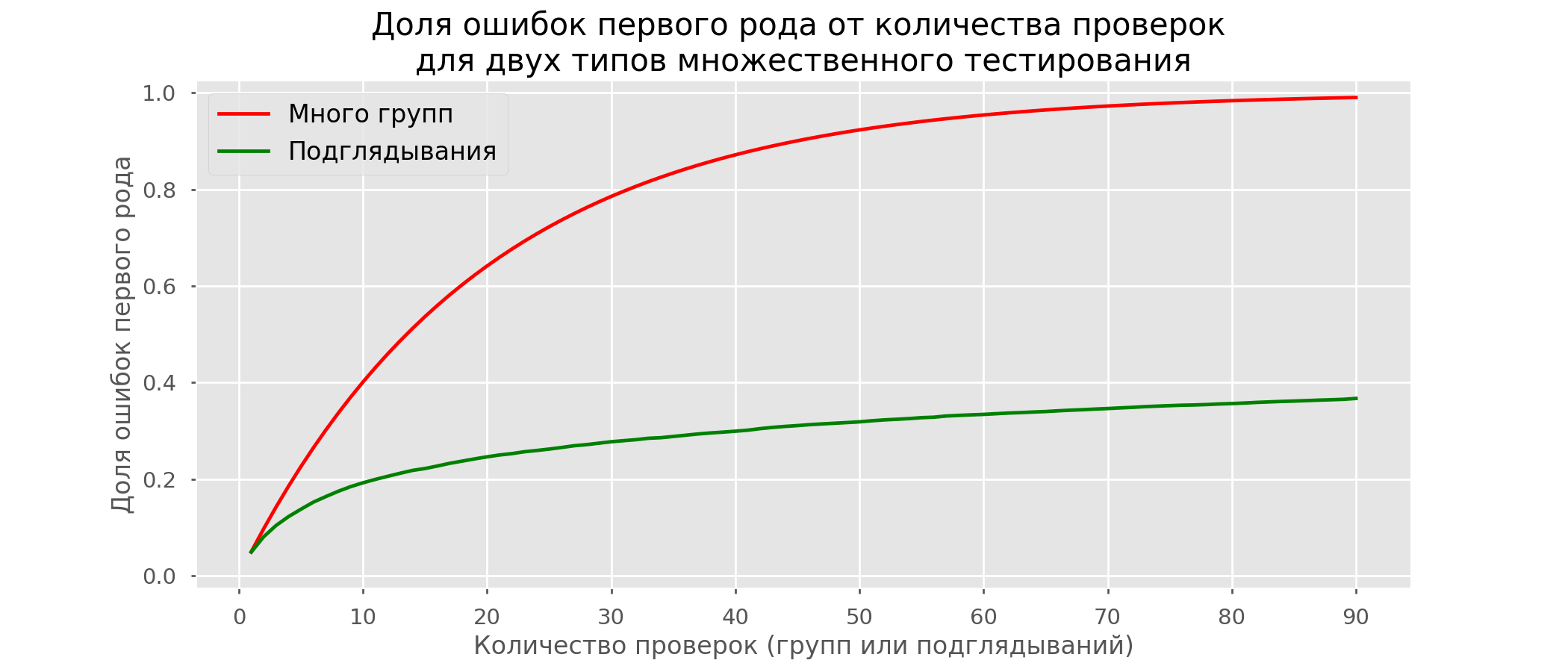Obwohl wir im Unendlichen und beim Gucken nahe an 1 kommen, wächst der Anteil der Fehler viel langsamer. Dies liegt daran, dass die Vergleiche in diesem Fall nicht mehr unabhängig sind.

Bayesianischer Ansatz und das Peeping-Problem

, A/B- . , . .

Frühe Testmethoden

Es gibt Testoptionen, mit denen Sie den Test vorzeitig durchführen können. Ich erzähle Ihnen von zwei davon: mit einem konstanten Signifikanzniveau (Pocock-Korrektur) und abhängig von der Anzahl der Peeps (O'Brien-Fleming-Korrektur). Genau genommen müssen Sie für beide Korrekturen die maximale Testdauer und die Anzahl der Überprüfungen zwischen Beginn und Ende des Tests im Voraus kennen. Darüber hinaus sollten Überprüfungen in ungefähr gleichen Zeitintervallen (oder in gleichen Mengen von Beobachtungen) erfolgen.

Pocock

Die Methode besteht darin, dass wir die Ergebnisse der Tests jeden Tag zusammenfassen, jedoch mit einem reduzierten (strengeren) Signifikanzniveau. Wenn wir beispielsweise wissen, dass wir nicht mehr als 30 Überprüfungen durchführen werden, sollte das Signifikanzniveau auf 0,006 gesetzt werden (ausgewählt in Abhängigkeit von der Anzahl der Peeps unter Verwendung der Monte-Carlo-Methode, d. H. Empirisch). In unserer Simulation erhalten wir 4% falsch positive Ergebnisse - anscheinend könnte der Schwellenwert erhöht werden.

Trotz der offensichtlichen Naivität wenden einige große Unternehmen diese spezielle Methode an. Es ist sehr einfach und zuverlässig, wenn Sie Entscheidungen zu sensiblen Metriken und zu viel Verkehr treffen. In Avito ist das Signifikanzniveau beispielsweise standardmäßig auf 0,005 festgelegt .

O'Brien-Fleming

Bei dieser Methode variiert das Signifikanzniveau in Abhängigkeit von der Verifizierungsnummer. Es ist notwendig, die Anzahl der Schritte (oder Peeps) im Test im Voraus zu bestimmen und das Signifikanzniveau für jeden von ihnen zu berechnen. Je früher wir versuchen, den Test abzuschließen, desto strenger werden die Kriterien angewendet. Schwellenwerte für Studentenstatistiken

Z_{s t e p}

$Z_{step}$ (einschließlich des Werts im letzten Schritt

Z_{l a s t_s t e p}

$Z_{last\_step}$ ), die dem gewünschten Signifikanzniveau entsprechen, hängen von der Verifizierungsnummer ab

s t e p_n u m b e r

$step\_number$ (nimmt Werte von 1 bis zur Gesamtzahl der Prüfungen an

t o t a l_s t e p s

$total\_steps$ einschließlich) und werden nach der empirisch ermittelten Formel berechnet:

Z_{l a s t_s t e p} = 2.2471 + \frac{0.3373}{t o t a l_s t e p s} - \frac{0.6331}{\sqrt{t o t a l_s t e p s}} Z_{s t e p} = Z_{l a s t_s t e p} \sqrt{\frac{t o t a l_s t e p s}{s t e p_n u m b e r}}

$Z_{last\_step} = 2.2471 + \frac {0.3373} {total\_steps} − \frac {0.6331} {\sqrt {total\_steps}} \\ Z_{step} = Z_{last\_step} \ {\sqrt { \frac {total\_steps} {step\_number}}}$

Quotencode

from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score
import matplotlib.pyplot as plt

# datapoints from https://www.aarondefazio.com/tangentially/?p=83
total_steps = [
    2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60
]
last_z = [
    1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081, 
    2.107, 2.123, 2.134, 2.143, 2.164, 2.17
]
features = [
    [1/t, 1/t**0.5] for t in total_steps
]
lr = LinearRegression()
lr.fit(features, last_z)
print(lr.coef_)  # [ 0.33729346, -0.63307934]
print(lr.intercept_)  # 2.247105015502784
print(explained_variance_score(lr.predict(features), last_z))  # 0.999894

total_steps_extended = np.arange(2, 80)
features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ]
plt.plot(total_steps_extended, lr.predict(features_extended))
plt.scatter(total_steps, last_z, s=30, color='black')
plt.show()

Die relevanten Signifikanzniveaus werden durch das Perzentil berechnet

p e r c

$perc$ Standardverteilung entsprechend dem Wert der Studentenstatistik

Z

$Z$ ::

perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2

Bei denselben Simulationen sieht es so aus:

Falsch positive Ergebnisse waren 501 von 10 Tausend oder die erwarteten 5%. Bitte beachten Sie, dass das Signifikanzniveau auch am Ende keinen Wert von 5% erreicht, da diese 5% bei allen Prüfungen "verschmiert" werden sollten. In der Firma verwenden wir genau diese Korrektur, wenn wir einen Test mit der Möglichkeit eines vorzeitigen Stopps durchführen. Über dieselben und andere Änderungen können Sie hier lesen .

Optimizely Methode

Optimizely , , . , . , . O'Brien-Fleming’a .

A / B-Testrechner

Die Besonderheiten unseres Produkts sind so, dass die Verteilung einer Metrik je nach Zielgruppe des Tests (z. B. Klassennummer) und Jahreszeit stark variiert. Daher ist es nicht möglich, die Regeln für das Enddatum des Tests im Sinne von "Der Test endet, wenn 1 Million Benutzer in jeder Gruppe eingegeben werden" oder "Der Test endet, wenn die Anzahl der gelösten Aufgaben 100 Millionen erreicht" zu akzeptieren. Das heißt, es wird funktionieren, aber in der Praxis müssen dafür zu viele Faktoren berücksichtigt werden:

Welche Klassen kommen in den Test?
Der Test wird an Lehrer oder Schüler verteilt.
akademische Jahreszeit;
Test für alle Benutzer oder nur für neue.

In unseren A / B-Testschemata müssen Sie das Enddatum jedoch immer im Voraus festlegen. Um die Dauer des Tests vorherzusagen, haben wir eine interne Anwendung entwickelt - den A / B-Testrechner. Basierend auf der Aktivität von Benutzern aus dem ausgewählten Segment im letzten Jahr berechnet die Anwendung den Zeitraum, für den der Test ausgeführt werden muss, um die Erhöhung in X% durch die ausgewählte Metrik signifikant zu korrigieren. Die Korrektur für mehrere Tests wird ebenfalls automatisch berücksichtigt und Schwellenwert-Signifikanzniveaus werden für einen frühen Teststopp berechnet.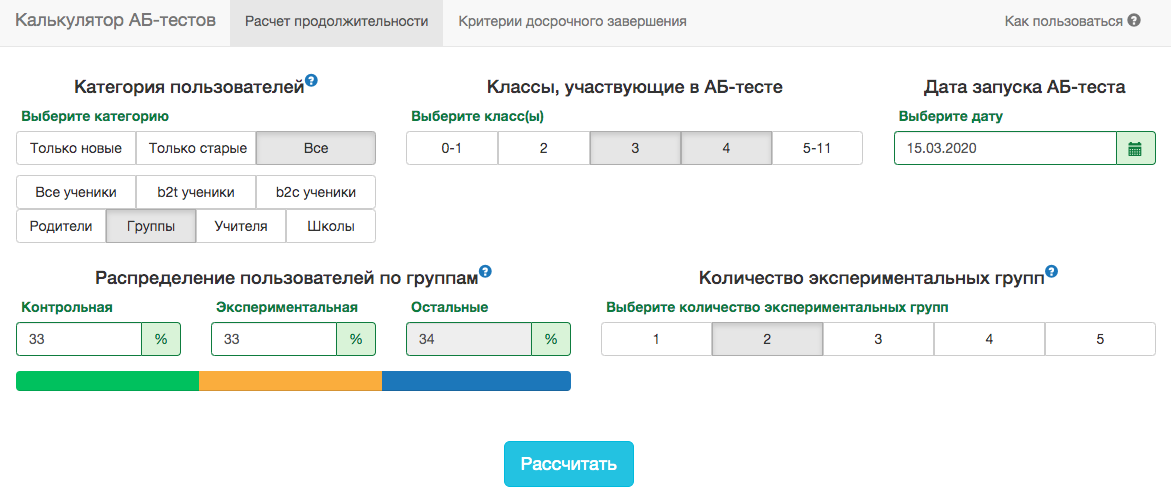

Alle Metriken werden auf der Ebene der Testobjekte berechnet. Wenn die Metrik die Anzahl der gelösten Probleme ist, ist dies im Test auf Lehrerebene die Summe der von seinen Schülern gelösten Probleme. Da wir das Schülerkriterium verwenden, können wir die vom Rechner benötigten Aggregate für alle möglichen Slices vorberechnen. Für jeden Tag ab Beginn des Tests müssen Sie die Anzahl der Personen im Test kennen

u s e r s_c n t

$users\_cnt$ , der Durchschnittswert der Metrik

m e t r i c_m e a n

$metric\_mean$ und seine Varianz

m e t r i c_s t d

$metric\_std$ . Festlegen der Anteile der Kontrollgruppe

c o n t r o l_g r o u p_s h a r e

$control\_group\_share$ Versuchsgruppe

e x p_g r o u p_s h a r e

$exp\_group\_share$ und erwarteter Gewinn aus dem Test

u p l i f t_e x p e c t e d

$uplift\_expected$ In Prozent können Sie die erwarteten Werte der Studentenstatistik berechnen

t t e s t_s t a t_v a l u e

$ttest\_stat\_value$ und den entsprechenden p-Wert für jeden Testtag:

t t e s t_s t a t_p r e c u r s o r = \frac{m e t r i c_m e a n \sqrt{u s e r s_c n t}}{m e t r i c_s t d} t t e s t_s t a t_v a l u e = \frac{t t e s t_s t a t_p r e c u r s o r}{\sqrt{\frac{1}{c o n t r o l_g r o u p_s h a r e} + \frac{1}{e x p_g r o u p_s h a r e}}} * u p l i f t_e x p e c t e d / 100

$ttest\_stat\_precursor = \frac{metric\_mean\ \sqrt {users\_cnt}}{metric\_std} \\ ttest\_stat\_value = \frac {ttest\_stat\_precursor} {\sqrt{ \frac{1} {control\_group\_share} + \frac {1} {exp\_group\_share}}} * uplift\_expected / 100$

Als nächstes ist es einfach, p-Werte für jeden Tag zu erhalten:

pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2

Wenn Sie den p-Wert und das Signifikanzniveau kennen und alle Korrekturen für jeden Testtag für jede Testdauer berücksichtigen, können Sie den minimalen Auftrieb berechnen, der festgestellt werden kann (in der englischen Literatur - MDE, minimaler nachweisbarer Effekt). Danach ist es einfach, das umgekehrte Problem zu lösen - die Anzahl der Tage zu bestimmen, die erforderlich sind, um die erwartete Hebung zu identifizieren.

Fazit

Abschließend möchte ich an die Hauptbotschaften des Artikels erinnern:

Wenn Sie die Durchschnittswerte der Metrik in Gruppen vergleichen, passt das Student-Kriterium höchstwahrscheinlich zu Ihnen. Die Ausnahme sind extrem kleine Stichprobengrößen (Dutzende von Beobachtungen) oder abnormale metrische Verteilungen (in der Praxis habe ich solche nicht gesehen).
Wenn der Test mehrere Gruppen enthält, verwenden Sie Korrekturen für das Testen mehrerer Hypothesen. Die einfachste Bonferroni-Korrektur reicht aus.
.
. .
. , , , , O'Brien-Fleming.
A/B-, A/A-.

Trotz alledem sollten Geschäft und gesunder Menschenverstand nicht aus mathematischen Gründen leiden. Manchmal ist es möglich, Funktionen für alle zu implementieren, die keinen signifikanten Anstieg des Tests zeigten. Einige Änderungen treten unvermeidlich ohne Tests auf. Wenn Sie jedoch Hunderte von Tests pro Jahr durchführen, ist deren genaue Analyse besonders wichtig. Andernfalls besteht das Risiko, dass die Anzahl der falsch positiven Tests mit wirklich nützlichen Tests vergleichbar ist.

Worauf wir bei der Berechnung der statistischen Signifikanz des A / B-Tests achten