👩🏾‍🏫 ⚗️ 🌘 3D mach es selbst. Teil 2: Es ist dreidimensional 🐾 👨🏽‍✈️ 😿

Im vorherigen Teil haben wir herausgefunden, wie zweidimensionale Objekte wie ein Pixel und eine Linie (Segment) angezeigt werden, aber Sie möchten wirklich schnell etwas Dreidimensionales erstellen. In diesem Artikel werden wir zum ersten Mal versuchen, ein 3D-Objekt auf dem Bildschirm anzuzeigen und uns mit neuen mathematischen Objekten wie einem Vektor und einer Matrix sowie einigen Operationen daran vertraut zu machen, aber nur mit denen, die in der Praxis anwendbar sind.

Im zweiten Teil werden wir betrachten:

Koordinatensystem
Punkt und Vektor
Die Matrix
Eckpunkte und Indizes
Visualisierungsförderer

Koordinatensystem

Es ist erwähnenswert, dass einige Beispiele und Vorgänge in den Artikeln ungenau und stark vereinfacht dargestellt sind, um das Verständnis des Materials zu verbessern und das Wesentliche zu erfassen. Sie können unabhängig voneinander die beste Lösung finden oder Fehler und Ungenauigkeiten im Demo-Code beheben. Bevor wir etwas Dreidimensionales zeichnen, ist es wichtig zu bedenken, dass alle dreidimensionalen Elemente auf dem Bildschirm in zweidimensionalen Pixeln angezeigt werden. Damit die von Pixeln gezeichneten Objekte dreidimensional aussehen, müssen wir ein wenig rechnen. Wir werden Formeln und Objekte nicht berücksichtigen, ohne ihre Anwendung zu sehen. Aus diesem Grund werden alle mathematischen Operationen, auf die Sie in diesem Artikel stoßen, in die Praxis umgesetzt, um ihr Verständnis zu vereinfachen.

Das erste, was zu verstehen ist, ist das Koordinatensystem. Lassen Sie uns sehen, welche Koordinatensysteme verwendet werden, und auch auswählen, welches für uns verwendet werden soll.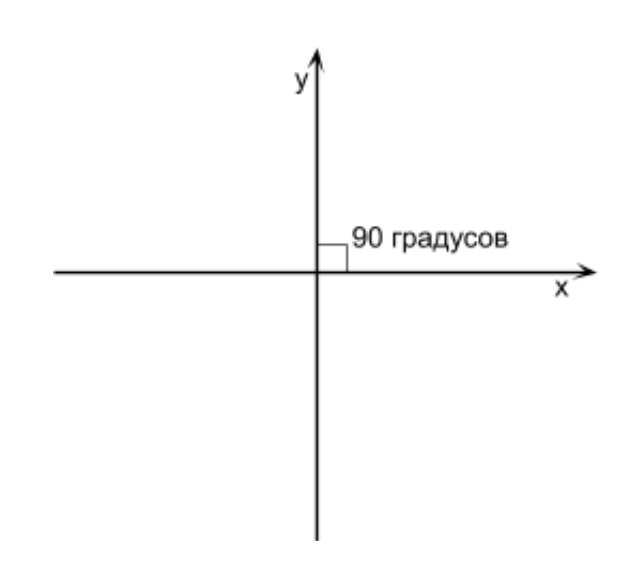

Was ist ein Koordinatensystem? Auf diese Weise können Sie die Position eines Punkts oder Charakters in einem aus Punkten bestehenden Spiel anhand von Zahlen bestimmen. Das Koordinatensystem hat zwei Richtungen der Achsen (wir werden sie als X, Y bezeichnen), wenn wir mit 2D-Grafiken arbeiten. Wenn wir ein 2D-Objekt mit einem größeren Y setzen und es höher wird als zuvor, bedeutet dies, dass die Y-Achse nach oben zeigt. Wenn wir dem Objekt ein größeres X geben und es mehr nach rechts zeigt, bedeutet dies, dass die X-Achse nach rechts gerichtet ist. Dies ist die Richtung der Achsen, und zusammen werden sie als Koordinatensystem bezeichnet. Wenn am Schnittpunkt der X- und Y-Achse ein Winkel von 90 Grad gebildet wird, wird ein solches Koordinatensystem als rechteckig (auch als kartesisches Koordinatensystem bezeichnet) bezeichnet (siehe Abbildung oben).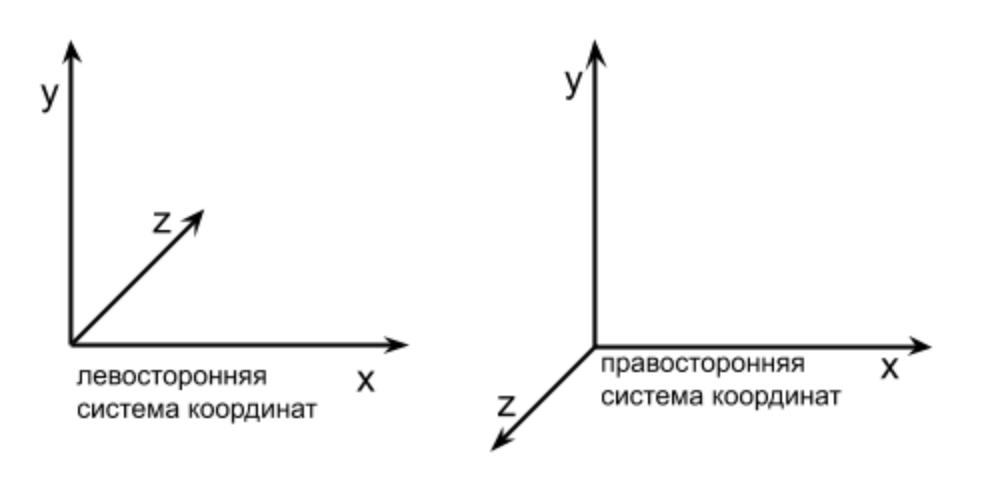

Aber es war ein Koordinatensystem in der 2D-Welt, in der dreidimensionalen erscheint eine andere Z-Achse. Wenn die Y-Achse (sie sagen Ordinate) es Ihnen ermöglicht, höher / niedriger zu zeichnen, die X-Achse (sie sagen auch die Abszisse) nach links / rechts, dann die Z-Achse (immer noch) say applicate) ermöglicht das Vergrößern / Verkleinern von Objekten. In dreidimensionalen Grafiken wird häufig (aber nicht immer) ein Koordinatensystem verwendet, bei dem die Y-Achse nach oben gerichtet ist, die X-Achse nach rechts gerichtet ist, Z jedoch entweder in die eine oder in die andere Richtung gerichtet sein kann. Deshalb werden wir die Koordinatensysteme in zwei Typen unterteilen - links und rechts (siehe Abbildung oben).

Wie aus der Abbildung ersichtlich ist, wird ein linkshändiges Koordinatensystem (sie sagen auch das linke Koordinatensystem) aufgerufen, wenn die Z-Achse von uns weg gerichtet ist (je größer das Z, desto weiter das Objekt). Wenn die Z-Achse auf uns gerichtet ist, ist dies ein rechtshändiges Koordinatensystem (sie sagen auch rechtes Koordinatensystem). Warum heißen sie so? Die linke, denn wenn die linke Hand mit der Handfläche nach oben und mit den Fingern in Richtung der X-Achse gerichtet ist, zeigt der Daumen die Z-Richtung an, dh sie zeigt in Richtung des Monitors, wenn X nach rechts gerichtet ist. Wenn Sie dasselbe mit Ihrer rechten Hand tun, wird die Z-Achse mit X nach rechts vom Monitor weg gerichtet. Mit den Fingern verwechselt? Im Internet gibt es verschiedene Möglichkeiten, Hand und Finger zu legen, um die erforderlichen Richtungen der Achsen zu erhalten. Dies ist jedoch kein obligatorischer Teil.

Für die Arbeit mit 3D-Grafiken gibt es viele Bibliotheken für verschiedene Sprachen, in denen verschiedene Koordinatensysteme verwendet werden. Beispielsweise verwendet die Direct3D-Bibliothek ein linkshändiges Koordinatensystem, und in OpenGL und WebGL ist das rechtshändige Koordinatensystem in VulkanAPI die Y-Achse nach unten (je kleiner das Y, desto höher das Objekt) und Z ist von uns, aber dies sind nur Konventionen, in den Bibliotheken können wir das angeben Koordinatensystem, das wir für bequemer halten.

Welches Koordinatensystem sollen wir wählen? Jeder ist geeignet, wir lernen nur und die Richtung der Achsen wird jetzt die Assimilation des Materials nicht beeinflussen. In den Beispielen verwenden wir das rechtshändige Koordinatensystem. Je weniger wir Z für den Punkt angeben, desto weiter ist es vom Bildschirm entfernt, während X, Y nach rechts / oben gerichtet sind.

Punkt und Vektor

Jetzt wissen Sie im Grunde, was Koordinatensysteme und Achsenrichtungen sind. Als nächstes müssen Sie analysieren, was ein Punkt und ein Vektor sind, weil Wir werden sie in diesem Artikel zum Üben brauchen. Ein Punkt im 3D-Raum ist ein durch [X, Y, Z] angegebener Ort. Zum Beispiel möchten wir unseren Charakter genau am Ursprung platzieren (möglicherweise in der Mitte des Fensters), dann ist seine Position [0, 0, 0], oder wir können sagen, dass er sich am Punkt [0, 0, 0] befindet. Jetzt wollen wir den Gegner links vom Spieler 20 Einheiten (zum Beispiel Pixel) platzieren, was bedeutet, dass er sich am Punkt [-20, 0, 0] befindet. Wir werden ständig mit Punkten arbeiten, um sie später genauer zu analysieren.

Was ist ein Vektor? Dies ist die Richtung. Im 3D-Raum wird es wie ein Punkt durch 3 Werte [X, Y, Z] beschrieben. Zum Beispiel müssen wir das Zeichen jede Sekunde um 5 Einheiten nach oben bewegen, damit wir Y ändern und jede Sekunde 5 hinzufügen, aber wir werden X und Z nicht berühren, diese Bewegung kann als Vektor geschrieben werden [0, 5, 0]. Wenn sich unser Charakter ständig um 2 Einheiten nach unten und um 1 nach rechts bewegt, sieht der Vektor seiner Bewegung folgendermaßen aus: [1, -2, 0]. Wir haben -2 geschrieben, weil Y nach unten nimmt ab.

Der Vektor hat keine Position und [X, Y, Z] geben die Richtung an. Ein Punkt kann zu einem Punkt hinzugefügt werden, um einen neuen Punkt um einen Vektor zu verschieben. Zum Beispiel habe ich oben bereits erwähnt, dass, wenn wir ein 3D-Objekt (zum Beispiel einen Spielcharakter) alle zwei Sekunden um 5 Einheiten nach oben bewegen möchten, der Verschiebungsvektor wie folgt lautet: [0, 5, 0]. Aber wie benutzt man es, um sich zu bewegen?

Angenommen, das Zeichen befindet sich am Punkt [5, 7, 0] und der Verschiebungsvektor ist [0, 5, 0]. Wenn wir dem Punkt einen Vektor hinzufügen, erhalten wir eine neue Spielerposition. Sie können einen Punkt mit einem Vektor oder einen Vektor mit einem Vektor gemäß der folgenden Regel hinzufügen.

Ein Beispiel für das Hinzufügen eines Punkts und eines Vektors :

[ 5, 7, 0 ] + [ 0, 5, 0 ] = [ 5 + 0, 7 + 5 , 0 + 0 ] = [5, 12, 0] - dies ist die neue Position unseres Charakters.

Wie Sie sehen können, hat sich unser Charakter um 5 Einheiten nach oben bewegt. Von hier aus erscheint ein neues Konzept - die Länge des Vektors. Jeder Vektor hat es, mit Ausnahme des Vektors [0, 0, 0], der als Nullvektor bezeichnet wird, ein solcher Vektor hat auch keine Richtung. Für den Vektor [0, 5, 0] beträgt die Länge 5, weil Ein solcher Vektor verschiebt den Punkt um 5 Einheiten nach oben. Der Vektor [0, 0, 10] hat eine Länge von 10, weil Es kann den Punkt entlang der Z-Achse um 10 verschieben. Der Vektor [12, 3, -4] sagt Ihnen jedoch nicht, wie lang er ist. Daher verwenden wir die Formel zur Berechnung der Länge des Vektors. Es stellt sich die Frage, warum wir die Länge des Vektors brauchen. Eine Anwendung besteht darin, herauszufinden, wie weit sich das Zeichen bewegen wird, oder die Geschwindigkeit von Zeichen mit einem längeren Verschiebungsvektor zu vergleichen, der schneller ist. Die Länge wird auch für einige Operationen an Vektoren verwendet.Die Länge des Vektors kann mit der folgenden Formel aus dem ersten Teil berechnet werden (nur Z wurde hinzugefügt):

L e n g t h = \sqrt{X^{2} + Y^{2} + Z^{2}}

$Length = \sqrt{X^2+Y^2+Z^2}$

Berechnen wir die Länge des Vektors mit der obigen Formel [6, 3, -8];

L e n g t h = \sqrt{6 * 6 + 3 * 3 + - 8 * - 8} = \sqrt{36 + 9 + 64} = \sqrt{109} \approx 10.44

$Length = \sqrt{6 * 6 + 3 * 3 + -8 * -8} = \sqrt{36 + 9 + 64} = \sqrt{109} ≈ 10.44$

Die Länge des Vektors [6, 3, -8] beträgt ungefähr 10,44.

Wir wissen bereits, was ein Punkt, ein Vektor ist, wie man einen Punkt und einen Vektor (oder 2 Vektoren) summiert und wie man die Länge eines Vektors berechnet. Fügen wir eine Vektorklasse hinzu und implementieren darin eine Summations- und Längenberechnung. Ich möchte auch darauf achten, dass wir keine Klasse für einen Punkt erstellen. Wenn wir einen Punkt benötigen, verwenden wir die Vektorklasse, weil Sowohl der Punkt als auch der Vektor speichern X, Y, Z, nur für den Punkt dieser Position und für den Vektor die Richtung.

Fügen Sie die Vektorklasse aus dem vorherigen Artikel zum Projekt hinzu. Sie können sie unterhalb der Drawer-Klasse hinzufügen. Ich habe Vector meine Klasse genannt und 3 Eigenschaften X, Y, Z hinzugefügt:

class Vector {
  x = 0;
  y = 0;
  z = 0;

  constructor(x, y, z) {
    this.x = x;
    this.y = y;
    this.z = z;
  }
}

Beachten Sie, dass die Felder x, y, z ohne die Funktionen von "Accessoren" sind, damit wir direkt auf die Daten im Objekt zugreifen können. Dies geschieht für einen schnelleren Zugriff. Später werden wir diesen Code noch weiter optimieren, aber lassen Sie ihn vorerst, um die Lesbarkeit zu verbessern.

Nun implementieren wir die Summation von Vektoren. Die Funktion benötigt 2 summierbare Vektoren, daher denke ich darüber nach, sie statisch zu machen. Der Hauptteil der Funktion arbeitet gemäß der obigen Formel. Das Ergebnis unserer Summierung ist ein neuer Vektor, mit dem wir zurückkehren werden:

static add(v1, v2) {
    return new Vector(
        v1.x + v2.x,
        v1.y + v2.y,
        v1.z + v2.z,
    );
}

Es bleibt die Funktion der Berechnung der Länge des Vektors zu implementieren. Auch hier implementieren wir alles nach den höheren Formeln:

getLength() {
    return Math.sqrt(
        this.x * this.x + this.y * this.y + this.z * this.z
    );
}

Schauen wir uns nun eine weitere Operation für den Vektor an, die etwas später in diesem und in den folgenden Artikeln benötigt wird - „Normalisierung des Vektors“. Angenommen, wir haben einen Charakter im Spiel, den wir mit den Pfeiltasten bewegen. Wenn wir nach oben drücken, bewegt es sich zum Vektor [0, 1, 0], wenn nach unten, dann [0, -1, 0], nach links [-1, 0, 0] und nach rechts [1, 0, 0]. Hier ist deutlich zu sehen, dass die Länge jedes der Vektoren 1 ist, dh die Geschwindigkeit des Charakters ist 1. Und lassen Sie uns eine diagonale Bewegung hinzufügen, wenn der Spieler den Pfeil nach oben und rechts klemmt, was ist der Verschiebungsvektor? Die naheliegendste Option ist der Vektor [1, 1, 0]. Wenn wir jedoch seine Länge berechnen, werden wir sehen, dass es ungefähr 1,414 entspricht. Es stellt sich heraus, dass unser Charakter diagonal schneller wird? Diese Option ist nicht geeignet, aber damit unser Charakter mit einer Geschwindigkeit von 1 diagonal verläuft, sollte der Vektor sein:[0,707, 0,707, 0]. Woher habe ich so einen Vektor? Ich nahm den Vektor [1, 1, 0] und normalisierte ihn, wonach ich [0,707, 0,707, 0] erhielt. Das heißt, Normalisierung ist die Reduktion eines Vektors auf eine Länge von 1 (Längeneinheit), ohne seine Richtung zu ändern. Beachten Sie, dass die Vektoren [0.707, 0.707, 0] und [1, 1, 0] in die gleiche Richtung zeigen, dh das Zeichen bewegt sich in beiden Fällen streng nach rechts, aber der Vektor [0.707, 0.707, 0] wird normalisiert und die Geschwindigkeit des Zeichens Jetzt ist es gleich 1, wodurch der Fehler bei beschleunigter diagonaler Bewegung beseitigt wird. Es wird immer empfohlen, den Vektor vor Berechnungen zu normalisieren, um verschiedene Arten von Fehlern zu vermeiden. Mal sehen, wie man einen Vektor normalisiert. Es ist notwendig, jede seiner Komponenten (X, Y, Z) durch ihre Länge zu teilen. Die Funktion, die Länge zu finden, ist bereits vorhanden, die Hälfte der Arbeit ist erledigt,Jetzt schreiben wir die Normalisierungsfunktion des Vektors (innerhalb der Vektorklasse):

normalize() {
    const length = this.getLength();
    
    this.x /= length;
    this.y /= length;
    this.z /= length;
    
    return this;
}

Die Normalisierungsmethode normalisiert den Vektor und gibt ihn zurück (dies). Dies ist erforderlich, damit in Zukunft die Normalisierung in Ausdrücken verwendet werden kann.

Jetzt, da wir wissen, was Normalisierung eines Vektors ist, und wir wissen, dass es besser ist, ihn durchzuführen, bevor wir den Vektor verwenden, stellt sich die Frage. Wenn die Normalisierung eines Vektors eine Reduzierung auf eine Längeneinheit ist, dh die Bewegungsgeschwindigkeit eines Objekts (Zeichens) gleich 1 ist, wie kann dann das Zeichen beschleunigt werden? Wenn Sie beispielsweise ein Zeichen mit einer Geschwindigkeit von 1 diagonal nach oben / rechts bewegen, ist sein Vektor [0,707, 0,707, 0], und welcher Vektor ist, wenn wir das Zeichen sechsmal schneller bewegen möchten? Zu diesem Zweck gibt es eine Operation namens "Multiplizieren eines Vektors mit einem Skalar". Der Skalar ist die übliche Zahl, mit der der Vektor multipliziert wird. Wenn der Skalar gleich 6 ist, wird der Vektor 6-mal länger und unser Charakter ist 6-mal schneller. Wie mache ich eine skalare Multiplikation? Dazu ist es notwendig, jede Komponente des Vektors mit einem Skalar zu multiplizieren. Zum Beispiel lösen wir das obige Problem:Wenn ein Zeichen, das sich zu einem Vektor [0,707, 0,707, 0] (Geschwindigkeit 1) bewegt, 6-mal beschleunigt werden muss, dh den Vektor mit Skalar 6 multiplizieren. Die Formel zum Multiplizieren des Vektors "V" mit Skalar "s" lautet wie folgt:

V * s = [\begin{matrix} V_{x} * s & V_{y} * s & V_{z} * s \end{matrix}]

$V * s = \begin{bmatrix}V_x * s&V_y*s&V_z*s\end{bmatrix}$

In unserem Fall wird es sein:

[\begin{matrix} 0.707 * 6 & 0.707 * 6 & 0 * 6 \end{matrix}] = [\begin{matrix} 4.242 & 4.242 & 0 \end{matrix}]

$\begin{bmatrix}0.707 * 6&0.707 * 6&0 * 6\end{bmatrix} = \begin{bmatrix}4.242&4.242&0\end{bmatrix}$ - ein neuer Verschiebungsvektor mit einer Länge von 6.

Es ist wichtig zu wissen, dass ein positiver Skalar den Vektor skaliert, ohne seine Richtung zu ändern. Wenn der Skalar jedoch negativ ist, skaliert er auch den Vektor (erhöht seine Länge), ändert jedoch zusätzlich die Richtung des Vektors in die entgegengesetzte Richtung.

Implementieren wir die Funktion des multiplyByScalarMultiplizierens eines Vektors mit einem Skalar in unserer Vektorklasse:

multiplyByScalar(s) {
    this.x *= s;
    this.y *= s;
    this.z *= s;
    
    return this;
}

Die Matrix

Wir haben ein bisschen mit Vektoren und einigen Operationen herausgefunden, die in diesem Artikel benötigt werden. Als nächstes müssen Sie sich mit Matrizen befassen.

Wir können sagen, dass eine Matrix das häufigste zweidimensionale Array ist. Es ist nur so, dass sie in der Programmierung den Begriff "zweidimensionales Array" verwenden und in der Mathematik die "Matrix". Warum werden Matrizen in der 3D-Programmierung benötigt? Wir werden dies analysieren, sobald wir lernen, ein wenig mit ihnen zu arbeiten.

Wir werden nur numerische Matrizen (ein Array von Zahlen) verwenden. Jede Matrix hat ihre eigene Größe (wie jedes zweidimensionale Array). Hier einige Beispiele für Matrizen:

M = [\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}]

$M=\begin{bmatrix}1&2&3\\4&5&6\end{bmatrix}$

2 mal 3 Matrix

M = [\begin{matrix} 2 & 4 & 3 \\ 3 & 4 & 4 \\ 5 & - 2 & 2 \end{matrix}]

$M=\begin{bmatrix}2&4&3\\3&4&4\\5&-2&2\end{bmatrix}$

3 mal 3 Matrix

M = [\begin{matrix} 2 \\ 3 \\ 0 \\ 5 \end{matrix}]

$M=\begin{bmatrix}2\\3\\0\\5\end{bmatrix}$

4 in 1 Matrix

M = [\begin{matrix} 5 & 0 & 7 \\ 2 & - 1 & 7 \\ 9 & 2 & 8 \\ 3 & 5 & 1 \end{matrix}]

$M=\begin{bmatrix}5&0&7\\2&-1&7\\9&2&8\\3&5&1\end{bmatrix}$

4 mal 3 Matrix

Von allen Operationen auf Matrizen betrachten wir jetzt nur die Multiplikation (der Rest später). Es stellt sich heraus, dass die Matrixmultiplikation nicht die einfachste Operation ist. Sie kann leicht verwirren, wenn Sie die Reihenfolge der Multiplikation nicht genau befolgen. Aber keine Sorge, Sie werden Erfolg haben, denn hier werden wir nur multiplizieren und zusammenfassen. Zunächst müssen wir uns einige Multiplikationsfunktionen merken, die wir benötigen:

Wenn wir versuchen, die Zahl A mit der Zahl B zu multiplizieren, ist dies dasselbe wie bei B * A. Wenn wir die Operanden neu anordnen und sich das Ergebnis bei keiner Aktion ändert, sagen sie, dass die Operation kommutativ ist. Beispiel: a + b = b + a die Operation ist kommutativ, a - b ≠ b - a die Operation ist nicht kommutativ, a * b = b * a die Operation des Multiplizierens von Zahlen ist kommutativ. Die Operation der Matrixmultiplikation ist also im Gegensatz zur Multiplikation von Zahlen nicht kommutativ. Das heißt, das Multiplizieren der Matrix M mit der Matrix N entspricht nicht der Multiplikation der Matrix N mit M.
Eine Matrixmultiplikation ist möglich, wenn die Anzahl der Spalten der ersten Matrix (links) gleich der Anzahl der Zeilen in der zweiten Matrix (rechts) ist.

Nun werfen wir einen Blick auf das zweite Merkmal der Matrixmultiplikation (wenn eine Multiplikation möglich ist). Hier einige Beispiele, die zeigen, wann eine Multiplikation möglich ist und wann nicht:

M_{1} = [\begin{matrix} 1 & 2 \end{matrix}]

$M_1=\begin{bmatrix}1&2\end{bmatrix}$

M_{2} = [\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}]

$M_2=\begin{bmatrix}1&2&3\\4&5&6\end{bmatrix}$

M1 M2 , .. 2 , 2 .

M_{1} = [\begin{matrix} 3 & 2 & 5 \\ 4 & 4 & 2 \\ - 7 & 4 & 5 \\ 7 & 9 & 4 \end{matrix}]

$M_1=\begin{bmatrix}3&2&5\\4&4&2\\-7&4&5\\7&9&4\end{bmatrix}$

M_{2} = [\begin{matrix} 1 & 0 \\ 4 & 5 \\ 6 & - 9 \end{matrix}]

$M_2=\begin{bmatrix}1&0\\4&5\\6&-9\end{bmatrix}$

1 2 , .. 3 , 3 .

M_{1} = [\begin{matrix} 5 & 4 \\ 0 & 3 \end{matrix}]

$M_1=\begin{bmatrix}5&4\\0&3\end{bmatrix}$

M_{2} = [\begin{matrix} 7 & 3 \\ 0 & 3 \\ 6 & 3 \end{matrix}]

$M_2=\begin{bmatrix}7&3\\0&3\\6&3\end{bmatrix}$

1 2 , .. 2 , 3 .

Ich denke, diese Beispiele haben das Bild ein wenig klarer gemacht, wenn eine Multiplikation möglich ist. Das Ergebnis der Matrixmultiplikation ist immer eine Matrix, deren Anzahl der Zeilen der Anzahl der Zeilen der 1. Matrix entspricht und deren Anzahl der Anzahl der Spalten der 2. Matrix entspricht. Wenn wir beispielsweise die Matrix 2 mit 6 und 6 mit 8 multiplizieren, erhalten wir eine Matrix der Größe 2 mit 8. Nun gehen wir direkt zur Multiplikation selbst über.

Bei der Multiplikation ist zu beachten, dass die Spalten und Zeilen in der Matrix ab 1 und im Array ab 0 nummeriert sind. Der erste Index im Matrixelement gibt die Zeilennummer und der zweite die Spaltennummer an. Das heißt, wenn das Matrixelement (Array-Element) wie folgt geschrieben ist: m28, bedeutet dies, dass wir uns der zweiten Zeile und der achten Spalte zuwenden. Da wir jedoch mit Arrays im Code arbeiten, beginnt die gesamte Indizierung von Zeilen und Spalten bei 0.

Versuchen wir, 2 Matrizen A und B mit bestimmten Größen und Elementen zu multiplizieren:

A = [\begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix}]

$A=\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}$

B = [\begin{matrix} 7 & 8 \\ 9 & 10 \end{matrix}]

$B=\begin{bmatrix}7&8\\9&10\end{bmatrix}$

Es ist ersichtlich, dass die Matrix A eine Größe von 3 mal 2 und die Matrix B eine Größe von 2 mal 2 hat. Eine Multiplikation ist möglich:

A * B = [\begin{matrix} 1 * 7 + 2 * 9 & 1 * 8 + 2 * 10 \\ 3 * 7 + 4 * 9 & 3 * 8 + 4 * 10 \\ 5 * 7 + 6 * 9 & 5 * 8 + 6 * 10 \end{matrix}] = [\begin{matrix} 25 & 28 \\ 57 & 64 \\ 89 & 100 \end{matrix}]

$A*B=\begin{bmatrix}1*7+2*9&1*8+2*10\\3*7+4*9&3*8+4*10\\5*7+6*9&5*8+6*10\end{bmatrix}=\begin{bmatrix}25&28\\57&64\\89&100\end{bmatrix}$

Wie Sie sehen können, haben wir eine 3 x 2-Matrix. Die Multiplikation ist zunächst verwirrend. Wenn Sie jedoch lernen möchten, wie man „ohne Stress“ multipliziert, müssen mehrere Beispiele gelöst werden. Hier ist ein weiteres Beispiel für die Multiplikation der Matrizen A und B:

A = [\begin{matrix} 3 & 2 \end{matrix}]

$A=\begin{bmatrix}3&2\end{bmatrix}$

B = [\begin{matrix} 2 & - 3 & 0 \\ 1 & 4 & - 2 \end{matrix}]

$B=\begin{bmatrix}2&-3&0\\1&4&-2\end{bmatrix}$

A * B = [\begin{matrix} 3 * 2 + 2 * 1 & 3 * - 3 + 2 * 4 & 3 * 0 + 2 * - 2 \end{matrix}] = [\begin{matrix} 8 & - 1 & - 4 \end{matrix}]

$A*B=\begin{bmatrix}3*2+2*1&3*-3+2*4&3*0+2*-2\end{bmatrix}=\begin{bmatrix}8&-1&-4\end{bmatrix}$

Wenn die Multiplikation nicht vollständig klar ist, ist es in Ordnung, weil Wir müssen uns nicht mit Blättern vermehren. Wir werden einmal die Matrixmultiplikationsfunktion schreiben und sie verwenden. Im Allgemeinen sind alle diese Funktionen bereits geschrieben, aber wir machen alles selbst.

Nun einige weitere Begriffe, die in Zukunft verwendet werden:

Eine quadratische Matrix ist eine Matrix, in der die Anzahl der Zeilen gleich der Anzahl der Spalten ist. Hier ein Beispiel für quadratische Matrizen:

[\begin{matrix} 2 & 3 \\ 6 & 4 \end{matrix}]

$\begin{bmatrix}2&3\\6&4\end{bmatrix}$

2 mal 2 quadratische Matrix

[\begin{matrix} 5 & 6 & 7 \\ 9 & 0 & - 2 \\ 4 & 5 & 1 \end{matrix}]

$\begin{bmatrix}5&6&7\\9&0&-2\\4&5&1\end{bmatrix}$

3 x 3 quadratische Matrix

[\begin{matrix} 5 & 6 & 7 & 3 \\ 9 & 0 & 2 & 1 \\ 4 & 5 & 1 & 3 \\ 1 & 7 & 9 & 8 \end{matrix}]

$\begin{bmatrix}5&6&7&3\\9&0&2&1\\4&5&1&3\\1&7&9&8\end{bmatrix}$

4 x 4 quadratische Matrix

Die Hauptdiagonale einer quadratischen Matrix heißt alle Elemente der Matrix, deren Zeilennummer gleich der Spaltennummer ist. Beispiele für Diagonalen (in diesem Beispiel ist die Hauptdiagonale mit Neunen gefüllt):

[\begin{matrix} 9 & 3 \\ 3 & 9 \end{matrix}]

$\begin{bmatrix}9&3\\3&9\end{bmatrix}$

[\begin{matrix} 9 & 3 & 3 \\ 3 & 9 & 3 \\ 3 & 3 & 9 \end{matrix}]

$\begin{bmatrix}9&3&3\\3&9&3\\3&3&9\end{bmatrix}$

[\begin{matrix} 9 & 3 & 3 & 3 \\ 3 & 9 & 3 & 3 \\ 3 & 3 & 9 & 3 \\ 3 & 3 & 3 & 9 \end{matrix}]

$\begin{bmatrix}9&3&3&3\\3&9&3&3\\3&3&9&3\\3&3&3&9\end{bmatrix}$

Eine Einheitsmatrix ist eine quadratische Matrix, in der alle Elemente der Hauptdiagonale 1 und alle anderen 0 sind. Beispiele für Einheitsmatrizen:

[\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}]

$\begin{bmatrix}1&0\\0&1\end{bmatrix}$

[\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}]

$\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$

[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}$

Es ist auch wichtig, sich an eine solche Eigenschaft zu erinnern, dass, wenn wir eine Matrix M mit einer Einheitsmatrix multiplizieren, deren Größe beispielsweise I heißt, wir die ursprüngliche Matrix M erhalten, zum Beispiel: M * I = M oder I * M = M. Das heißt, Das Multiplizieren der Matrix mit der Identitätsmatrix hat keinen Einfluss auf das Ergebnis. Wir werden später auf die Identitätsmatrix zurückkommen. In der 3D-Programmierung verwenden wir häufig eine 4 x 4-Quadratmatrix.

Schauen wir uns nun an, warum wir Matrizen benötigen und warum wir sie multiplizieren. In der 3D-Programmierung gibt es viele verschiedene 4 x 4-Matrizen, die, wenn sie mit einem Vektor oder Punkt multipliziert werden, die von uns benötigten Aktionen ausführen. Zum Beispiel müssen wir das Zeichen im dreidimensionalen Raum um die X-Achse drehen. Wie geht das? Multiplizieren Sie den Vektor mit einer speziellen Matrix, die für die Drehung um die X-Achse verantwortlich ist. Wenn Sie einen Punkt um den Ursprung verschieben und drehen müssen, müssen Sie diesen Punkt mit einer speziellen Matrix multiplizieren. Matrizen haben eine hervorragende Eigenschaft - sie kombinieren Transformationen (wir werden in diesem Artikel darauf eingehen). Angenommen, wir benötigen ein Zeichen, das aus 100 Punkten (Eckpunkten, aber auch etwas niedriger) besteht, in der Anwendung, erhöhen Sie es um das Fünffache, drehen Sie es dann um 90 Grad X und bewegen Sie es dann um 30 Einheiten nach oben.Wie bereits erwähnt, gibt es für verschiedene Aktionen bereits spezielle Matrizen, die wir berücksichtigen werden. Um die obige Aufgabe abzuschließen, durchlaufen wir beispielsweise alle 100 Punkte und multiplizieren jeweils zuerst mit der 1. Matrix, um das Zeichen zu erhöhen. Dann multiplizieren wir mit der 2. Matrix, um 90 Grad in X zu drehen, und multiplizieren dann mit 3 th, um 30 Einheiten nach oben zu bewegen. Insgesamt haben wir für jeden Punkt 3 Matrixmultiplikationen und 100 Punkte, was bedeutet, dass es 300 Multiplikationen gibt. Wenn wir jedoch die Matrizen nehmen und multiplizieren, um sie um das Fünffache zu erhöhen, drehen Sie sie um 90 Grad entlang X und bewegen Sie sich um 30 Einheiten. Nach oben erhalten wir eine Matrix, die alle diese Aktionen enthält. Wenn Sie einen Punkt mit einer solchen Matrix multiplizieren, ist der Punkt dort, wo er benötigt wird. Berechnen wir nun, wie viele Aktionen ausgeführt werden: 2 Multiplikationen für 3 Matrizen und 100 Multiplikationen für 100 Punkte.Insgesamt 102 Multiplikationen sind definitiv besser als 300 Multiplikationen davor. Der Moment, in dem wir 3 Matrizen multipliziert haben, um verschiedene Aktionen in einer Matrix zu kombinieren, wird als Kombination von Transformationen bezeichnet und wir werden es definitiv mit einem Beispiel tun.

Wie man die Matrix mit der Matrix multipliziert, haben wir untersucht, aber der oben gelesene Absatz spricht von der Multiplikation der Matrix mit einem Punkt oder Vektor. Um einen Punkt oder Vektor zu multiplizieren, reicht es aus, sie als Matrix darzustellen.

Zum Beispiel haben wir einen Vektor [10, 2, 5] und es gibt eine Matrix:

[\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}]

$\begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix}$

Es ist ersichtlich, dass der Vektor durch eine Matrix von 1 mal 3 oder durch eine Matrix von 3 mal 1 dargestellt werden kann. Daher können wir den Vektor mit einer Matrix von 2 Möglichkeiten multiplizieren:

[\begin{matrix} 10 & 2 & 5 \end{matrix}] * [\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}]

$\begin{bmatrix}10&2&5\end{bmatrix} * \begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix}$

Hier haben wir den Vektor als 1 x 3-Matrix dargestellt (sie sagen auch einen Zeilenvektor). Eine solche Multiplikation ist möglich, weil Die erste Matrix (Zeilenvektor) hat 3 Spalten und die zweite Matrix hat 3 Zeilen.

[\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}] * [\begin{matrix} 10 \\ 2 \\ 5 \end{matrix}]

$\begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix} * \begin{bmatrix}10\\2\\5\end{bmatrix}$

Hier haben wir den Vektor als 3 x 1-Matrix dargestellt (sie sagen auch einen Spaltenvektor). Eine solche Multiplikation ist möglich, weil In der ersten Matrix gibt es 3 Spalten und in der zweiten (Spaltenvektor) 3 Zeilen.

Wie Sie sehen können, können wir den Vektor als Zeilenvektor darstellen und mit einer Matrix multiplizieren oder den Vektor als Spaltenvektor darstellen und die Matrix damit multiplizieren. Überprüfen wir, ob das Ergebnis der Multiplikation in beiden Fällen gleich ist:

Multiplizieren Sie den Zeilenvektor mit der Matrix:

[\begin{matrix} 10 & 2 & 5 \end{matrix}] * [\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}] =

$\begin{bmatrix}10&2&5\end{bmatrix} * \begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix} =$

= [\begin{matrix} 10 * 1 + 2 * 2 + 5 * 0 & 10 * 2 + 2 * 2 + 5 * 4 & 10 * 1 + 2 * 1 + 5 * 3 \end{matrix}] = [\begin{matrix} 14 & 44 & 27 \end{matrix}]

$= \begin{bmatrix}10*1+2*2+5*0&10*2+2*2+5*4&10*1+2*1+5*3\end{bmatrix} = \begin{bmatrix}14&44&27\end{bmatrix}$

Multiplizieren Sie nun die Matrix mit dem Spaltenvektor:

[\begin{matrix} 1 & 2 & 1 \\ 2 & 2 & 1 \\ 0 & 4 & 3 \end{matrix}] * [\begin{matrix} 10 \\ 2 \\ 5 \end{matrix}] = [\begin{matrix} 1 * 10 + 2 * 5 + 1 * 5 \\ 2 * 10 + 2 * 2 + 1 * 5 \\ 0 * 10 + 4 * 2 + 3 * 5 \end{matrix}] = [\begin{matrix} 19 \\ 29 \\ 23 \end{matrix}]

$\begin{bmatrix}1&2&1\\2&2&1\\0&4&3\end{bmatrix} * \begin{bmatrix}10\\2\\5\end{bmatrix}=\begin{bmatrix}1*10+2*5+1*5\\2*10+2*2+1*5\\0*10+4*2+3*5\end{bmatrix}=\begin{bmatrix}19\\29\\23\end{bmatrix}$

Wir sehen, dass wir durch Multiplikation des Zeilenvektors mit der Matrix und der Matrix mit dem Spaltenvektor völlig unterschiedliche Ergebnisse erhalten (wir erinnern uns an die Kommutativität). Daher gibt es in der 3D-Programmierung Matrizen, die nur mit einem Zeilenvektor oder nur mit einem Spaltenvektor multipliziert werden sollen. Wenn wir die für den Zeilenvektor vorgesehene Matrix mit dem Spaltenvektor multiplizieren, erhalten wir ein Ergebnis, das uns nichts gibt. Verwenden Sie die für Sie geeignete Vektor- / Punktdarstellung (Zeile oder Spalte). Verwenden Sie in Zukunft nur die entsprechenden Matrizen für Ihre Vektor- / Punktdarstellung. Direct3D verwendet beispielsweise eine Zeichenfolgendarstellung von Vektoren, und alle Matrizen in Direct3D sind so konzipiert, dass sie einen Zeilenvektor mit einer Matrix multiplizieren. OpenGL verwendet eine Darstellung eines Vektors (oder Punkts) als Spalte.und alle Matrizen sind so ausgelegt, dass sie die Matrix mit einem Spaltenvektor multiplizieren. In den Artikeln werden wir den Spaltenvektor verwenden und die Matrix mit dem Spaltenvektor multiplizieren.

Um zusammenzufassen, was wir über die Matrix gelesen haben.

Um eine Aktion für einen Vektor (oder Punkt) auszuführen, gibt es spezielle Matrizen, von denen wir einige in diesem Artikel sehen werden.
Um die Transformation (Verschiebung, Drehung usw.) zu kombinieren, können wir die Matrizen jeder Transformation miteinander multiplizieren und eine Matrix erhalten, die alle Transformationen zusammen enthält.
In der 3D-Programmierung werden ständig 4 x 4 Quadratmatrizen verwendet.
Wir können die Matrix mit einem Vektor (oder Punkt) multiplizieren, indem wir sie als Spalte oder Zeile darstellen. Für den Spaltenvektor und den Zeilenvektor müssen Sie jedoch unterschiedliche Matrizen verwenden.

Nach einer kleinen Analyse der Matrizen fügen wir eine 4 x 4-Matrixklasse hinzu und implementieren Methoden zum Multiplizieren der Matrix mit der Matrix und des Vektors mit der Matrix. Wir werden die Größe der Matrix 4 mal 4 verwenden, weil Alle Standardmatrizen, die für verschiedene Aktionen (Bewegung, Drehung, Skalierung, ...) verwendet werden, haben eine solche Größe, dass wir keine Matrizen einer anderen Größe benötigen.

Fügen wir dem Projekt die Matrix-Klasse hinzu. Dennoch wird die Klasse für die Arbeit mit 4 x 4-Matrizen manchmal Matrix4 genannt, und diese 4 im Titel gibt Auskunft über die Größe der Matrix (sie sagen auch die Matrix 4. Ordnung). Alle Matrixdaten werden in einem zweidimensionalen 4 x 4-Array gespeichert.

Wir wenden uns der Implementierung von Multiplikationsoperationen zu. Ich empfehle hierfür keine Loops. Um die Leistung zu verbessern, müssen wir alle Zeile für Zeile multiplizieren - dies geschieht aufgrund der Tatsache, dass alle Multiplikationen mit Matrizen fester Größe stattfinden. Ich werde Zyklen für die Multiplikation verwenden, nur um die Menge an Code zu sparen, können Sie die gesamte Multiplikation ohne Zyklen schreiben. Mein Multiplikationscode sieht folgendermaßen aus:

class Matrix {
  static multiply(a, b) {
    const m = [
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
    ];

    for (let i = 0; i < 4; i++) {
      for (let j = 0; j < 4; j++) {
        m[i][j] = a[i][0] * b[0][j] +
          a[i][1] * b[1][j] +
          a[i][2] * b[2][j] +
          a[i][3] * b[3][j];
      }
    }

    return m;
  }
}

Wie Sie sehen können, nimmt die Methode die Matrizen a und b, multipliziert sie und gibt das Ergebnis in demselben Array 4 mit 4 zurück. Zu Beginn der Methode habe ich eine Matrix m erstellt, die mit Nullen gefüllt ist. Dies ist jedoch nicht erforderlich. Daher wollte ich zeigen, welche Dimension das Ergebnis haben wird Sie können ein 4 x 4-Array ohne Daten erstellen.

Jetzt müssen Sie die Multiplikation der Matrix mit dem Spaltenvektor wie oben beschrieben implementieren. Wenn Sie den Vektor jedoch als Spalte darstellen, erhalten Sie eine Matrix der Form:

[\begin{matrix} x \\ y \\ z \end{matrix}]

$\begin{bmatrix}x\\y\\z\end{bmatrix}$
mit denen wir mit 4 mal 4 Matrizen multiplizieren müssen, um verschiedene Aktionen auszuführen. In diesem Beispiel ist jedoch deutlich zu sehen, dass eine solche Multiplikation nicht durchgeführt werden kann, da der Spaltenvektor 3 Zeilen und die Matrix 4 Spalten hat. Was ist dann zu tun? Ein viertes Element wird benötigt, dann hat der Vektor 4 Zeilen, was der Anzahl der Spalten in der Matrix entspricht. Fügen wir dem Vektor einen solchen 4. Parameter hinzu und nennen ihn W, jetzt haben wir alle 3D-Vektoren in der Form [X, Y, Z, W] und diese Vektoren können bereits mit 4 mit 4 multipliziert werden. Tatsächlich ist die W-Komponente ein tieferer Zweck, aber wir werden ihn im nächsten Teil kennenlernen (nicht umsonst haben wir eine 4 mal 4 Matrix, nicht 3 mal 3 Matrix). Fügen Sie der Vektorklasse hinzu, die wir über der w-Komponente erstellt haben. Der Anfang der Vector-Klasse sieht nun folgendermaßen aus:

class Vector {
    x = 0;
    y = 0;
    z = 0;
    w = 1;

    constructor(x, y, z, w = 1) {
        this.x = x;
        this.y = y;
        this.z = z;
        this.w = w;
    }

Ich habe W auf eins initialisiert, aber warum 1? Wenn wir uns ansehen, wie die Komponenten der Matrix und des Vektors multipliziert werden (das folgende Codebeispiel), können Sie sehen, dass wenn Sie W auf 0 oder einen anderen Wert als 1 setzen, das Multiplizieren dieses W das Ergebnis beeinflusst, dies jedoch nicht Wir wissen, wie man es benutzt, und wenn wir es zu 1 machen, wird es im Vektor sein, aber das Ergebnis wird sich in keiner Weise ändern.

Nun zurück zur Matrix und Implementierung in der Matrix-Klasse (Sie können auch in der Vector-Klasse keinen Unterschied feststellen). Die Matrix wird mit einem Vektor multipliziert, was dank W bereits möglich ist:

static multiplyVector(m, v) {
  return new Vector(
    m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
    m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
    m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
    m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
  )
}

Bitte beachten Sie, dass wir die Matrix als 4 x 4-Array und den Vektor als Objekt mit den Eigenschaften x, y, z, w dargestellt haben. In Zukunft werden wir den Vektor ändern und er wird auch durch ein 1 x 4-Array dargestellt, weil es wird die Multiplikation beschleunigen. Um nun besser zu sehen, wie die Multiplikation erfolgt, und das Verständnis des Codes zu verbessern, werden wir den Vektor nicht ändern.

Wir haben den Code für die Matrixmultiplikation untereinander und die Matrixvektormultiplikation geschrieben, aber es ist immer noch nicht klar, wie dies uns bei dreidimensionalen Grafiken helfen wird.

Ich möchte Sie auch daran erinnern, dass ich einen Vektor sowohl als Punkt (Position im Raum) als auch als Richtung bezeichne, weil Beide Objekte enthalten die gleiche Datenstruktur x, y, z und das neu eingeführte w.

Schauen wir uns einige der Matrizen an, die grundlegende Operationen an Vektoren ausführen. Die erste dieser Matrizen ist die Übersetzungsmatrix. Multipliziert man die Verschiebungsmatrix mit einem Vektor (Ort), verschiebt sie sich um die angegebene Anzahl von Einheiten im Raum. Und hier ist die Verschiebungsmatrix:

[\begin{matrix} 1 & 0 & 0 & d x \\ 0 & 1 & 0 & d y \\ 0 & 0 & 1 & d z \\ 0 & 0 & 0 & 1 \end{matrix}]

$\begin{bmatrix}1&0&0&dx\\0&1&0&dy\\0&0&1&dz\\0&0&0&1\end{bmatrix}$

Wenn dx, dy, dz Verschiebungen entlang der x-, y- und z-Achse bedeuten, ist diese Matrix so ausgelegt, dass sie mit einem Spaltenvektor multipliziert wird. Solche Matrizen finden Sie im Internet oder in jeder Literatur zur 3D-Programmierung. Wir müssen sie nicht selbst erstellen. Nehmen Sie sie jetzt als die Formeln, die Sie in der Schule verwenden und die Sie nur kennen oder verstehen müssen, warum Sie sie verwenden sollen. Lassen Sie uns prüfen, ob beim Multiplizieren einer solchen Matrix mit einem Vektor tatsächlich ein Offset auftritt. Nehmen wir als Vektor, wir bewegen den Vektor [10, 10, 10, 1] (wir lassen immer den 4. Parameter W immer 1), nehmen wir an, dass dies die Position unseres Charakters im Spiel ist und wir wollen ihn 10 Einheiten nach oben verschieben, 5 Einheiten rechts und 1 Einheit vom Bildschirm entfernt. Dann ist der Verschiebungsvektor wie folgt [10, 5, -1] (-1, weil wir ein rechtshändiges Koordinatensystem haben und das weitere Z,je kleiner es ist). Wenn wir das Ergebnis ohne Matrizen berechnen, durch die übliche Summe von Vektoren. Dies führt zu folgendem Ergebnis: [10 + 10, 10 + 5, 10 + -1, 1] = [20, 15, 9, 1] - dies sind die neuen Koordinaten unseres Charakters. Multipliziert man die obige Matrix mit den Anfangskoordinaten [10, 10, 10, 1], sollte man das gleiche Ergebnis erhalten. Überprüfen wir dies im Code und schreiben die Multiplikation nach den Klassen Drawer, Vector und Matrix:

const translationMatrix = [
  [1, 0, 0, 10],
  [0, 1, 0, 5],
  [0, 0, 1, -1],
  [0, 0, 0, 1],
]
        
const characterPosition = new Vector(10, 10, 10)
        
const newCharacterPosition = Matrix.multiplyVector(
  translationMatrix, characterPosition
)
console.log(newCharacterPosition)

In diesem Beispiel haben wir den gewünschten Zeichenversatz (translationMatrix) in die Verschiebungsmatrix eingesetzt, ihre Anfangsposition (characterPosition) initialisiert und dann mit der Matrix multipliziert. Das Ergebnis wurde über console.log ausgegeben (dies ist die Debug-Ausgabe in JS). Wenn Sie Nicht-JS verwenden, geben Sie X, Y, Z selbst mit den Werkzeugen Ihrer Sprache aus. Das Ergebnis, das wir in der Konsole erhalten haben: [20, 15, 9, 1], alles stimmt mit dem Ergebnis überein, das wir oben berechnet haben. Möglicherweise haben Sie die Frage, warum Sie das gleiche Ergebnis erzielen, indem Sie den Vektor mit einer speziellen Matrix multiplizieren, wenn wir es viel einfacher erhalten, indem wir den Vektor komponentenweise mit einem Versatz summieren. Die Antwort ist nicht die einfachste und wir werden sie genauer diskutieren, aber jetzt kann festgestellt werden, dass wir, wie bereits erwähnt, Matrizen mit verschiedenen Transformationen untereinander kombinieren können.Dadurch werden so viele Berechnungen reduziert. Im obigen Beispiel haben wir die translationMatrix-Matrix manuell als Array erstellt und dort den erforderlichen Offset ersetzt. Da wir diese und andere Matrizen jedoch häufig verwenden, fügen wir sie in eine Methode in der Matrix-Klasse ein und übergeben den Offset mit Argumenten an sie:

static getTranslation(dx, dy, dz) {
  return [
    [1, 0, 0, dx],
    [0, 1, 0, dy],
    [0, 0, 1, dz],
    [0, 0, 0, 1],
  ]
}

Wenn Sie sich die Verschiebungsmatrix genauer ansehen, werden Sie sehen, dass sich dx, dy, dz in der letzten Spalte befinden. Wenn wir uns den Code zum Multiplizieren der Matrix mit einem Vektor ansehen, werden wir feststellen, dass diese Spalte mit der W-Komponente des Vektors multipliziert wird. Und wenn es zum Beispiel 0 wäre, dann dx, dy, dz, würden wir mit 0 multiplizieren und die Bewegung würde nicht funktionieren. Aber wir können W gleich 0 machen, wenn wir die Richtung in der Vector-Klasse speichern wollen, weil Es ist unmöglich, die Richtung zu verschieben, also würden wir uns schützen, und selbst wenn wir eine solche Richtung mit der Verschiebungsmatrix multiplizieren, wird dies den Richtungsvektor nicht brechen, weil Alle Bewegungen werden mit 0 multipliziert.

Insgesamt können wir eine solche Regel anwenden. Wir erstellen einen Ort wie diesen:

new Vector(x, y, z, 1) // 1    ,

Und wir werden die Richtung wie folgt festlegen:

new Vector(x, y, z, 0)

Wir können also zwischen Ort und Richtung unterscheiden, und wenn wir die Richtung mit der Verschiebungsmatrix multiplizieren, brechen wir den Richtungsvektor nicht versehentlich.

Eckpunkte und Indizes

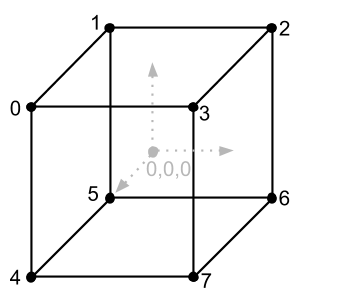
Bevor wir sehen, was andere Matrizen sind, werden wir uns ein wenig damit befassen, wie wir unser vorhandenes Wissen anwenden können, um etwas Dreidimensionales auf dem Bildschirm anzuzeigen. Alles, was wir vorher abgeleitet haben, sind Linien und Pixel. Verwenden wir diese Tools nun, um beispielsweise einen Würfel abzuleiten. Dazu müssen wir herausfinden, woraus ein dreidimensionales Modell besteht. Die grundlegendste Komponente eines 3D-Modells sind die Punkte (wir werden die Eckpunkte unten nennen), entlang derer wir es zeichnen können. Dies sind in der Tat viele Positionsvektoren. Wenn wir sie korrekt mit Linien verbinden, erhalten wir ein 3D-Modell (Modellgitter) ) auf dem Bildschirm wird es ohne Textur und ohne viele andere Eigenschaften sein, aber alles hat seine Zeit. Schauen Sie sich den Würfel an, den wir ausgeben möchten, und versuchen Sie zu verstehen, wie viele Scheitelpunkte er hat: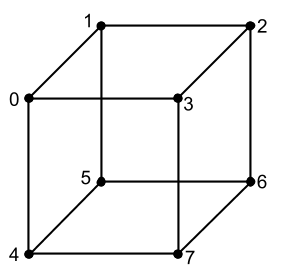

Im Bild sehen wir, dass der Würfel 8 Eckpunkte hat (der Einfachheit halber habe ich sie nummeriert). Und alle Eckpunkte sind durch Linien (Kanten des Würfels) miteinander verbunden. Das heißt, um den Würfel zu beschreiben und mit Linien zu zeichnen, benötigen wir 8 Koordinaten jedes Scheitelpunkts, und wir müssen auch angeben, von welchem Scheitelpunkt aus wir die Linie zeichnen, um einen Würfel zu erstellen. Wenn wir beispielsweise die Scheitelpunkte falsch verbinden, zeichnen Sie beispielsweise eine Linie aus dem Scheitelpunkt 0 bis Vertex 6, dann ist es definitiv kein Würfel, sondern ein anderes Objekt. Beschreiben wir nun die Koordinaten jedes der 8 Eckpunkte. In modernen Grafiken können 3D-Modelle aus Zehntausenden von Eckpunkten bestehen, und natürlich schreibt niemand sie manuell vor. Modelle werden in 3D-Editoren gezeichnet. Wenn das 3D-Modell exportiert wird, enthält es bereits alle Scheitelpunkte im Code. Wir müssen sie nur laden und zeichnen. Derzeit lernen wir jedoch und können die Formate von 3D-Modellen nicht lesen. Daher werden wir den Würfel manuell beschreiben.er ist sehr einfach.

Stellen Sie sich vor, der Würfel oben befindet sich in der Mitte der Koordinaten, seine Mitte befindet sich am Punkt 0, 0, 0 und sollte um diese Mitte herum angezeigt werden:

Beginnen wir mit Scheitelpunkt 0 und lassen Sie unseren Würfel sehr klein sein, um jetzt keine großen Werte zu schreiben. Die Abmessungen meines Würfels sind 2 breit, 2 hoch und 2 tief, d. H. 2 mal 2 mal 2. Das Bild zeigt, dass der Scheitelpunkt 0 etwas links von der Mitte 0, 0, 0 liegt, also werde ich X = -1 setzen, weil links, je kleiner X, auch der Scheitelpunkt 0 ist etwas höher als der Mittelpunkt 0, 0, 0, und in unserem Koordinatensystem setze ich meinen Scheitelpunkt Y = 1, auch Z für Scheitelpunkt 0, etwas näher am Bildschirm, je höher die Position, desto größer Y in Bezug auf den Punkt 0, 0, 0 ist er also gleich Z = 1, da im rechtshändigen Koordinatensystem Z mit der Annäherung des Objekts zunimmt. Als Ergebnis haben wir die Koordinaten -1, 1, 1 für den Nullpunkt erhalten. Machen wir dasselbe für die verbleibenden 7 Eckpunkte und speichern sie in einem Array, damit Sie mit ihnen in einer Schleife arbeiten können.Ich habe dieses Ergebnis erhalten (ein Array kann unter den Klassen Drawer, Vector, Marix erstellt werden):

// Cube vertices
const vertices = [
  new Vector(-1, 1, 1), // 0 
  new Vector(-1, 1, -1), // 1 
  new Vector(1, 1, -1), // 2 
  new Vector(1, 1, 1), // 3 
  new Vector(-1, -1, 1), // 4 
  new Vector(-1, -1, -1), // 5 
  new Vector(1, -1, -1), // 6 
  new Vector(1, -1, 1), // 7 
];

Ich habe jeden Scheitelpunkt in eine Instanz der Vector-Klasse eingefügt. Dies ist nicht die beste Option für die Leistung (besser in einem Array), aber jetzt ist unser Ziel, herauszufinden, wie alles funktioniert.

Nehmen wir nun die Koordinaten der Eckpunkte des Würfels als Pixel, die wir auf dem Bildschirm zeichnen. In diesem Fall sehen wir, dass die Größe des Würfels 2 x 2 x 2 Pixel beträgt. Wir haben so einen kleinen Würfel erstellt Schauen Sie sich die Arbeit der Skalierungsmatrix an, mit der wir sie erweitern werden. In Zukunft ist es sehr empfehlenswert, Modelle klein zu machen, sogar kleiner als unsere, um sie mit nicht sehr unterschiedlichen Skalaren auf die gewünschte Größe zu vergrößern.

Es ist nur so, dass das Zeichnen der Würfelpunkte mit Pixeln nicht sehr klar ist, weil Alles, was wir sehen werden, sind 8 Pixel, eines für jeden Scheitelpunkt. Es ist viel besser, einen Würfel mit Linien mit der Funktion drawLine aus dem vorherigen Artikel zu zeichnen. Dazu müssen wir jedoch verstehen, von welchen Eckpunkten zu welchen Linien wir gehen. Schauen Sie sich das Bild des Würfels mit den Indizes noch einmal an und wir werden sehen, dass es aus 12 Linien (oder Kanten) besteht. Es ist auch sehr leicht zu erkennen, dass wir die Koordinaten des Anfangs und des Endes jeder Zeile kennen. Beispielsweise sollte eine der Linien (oben in der Nähe) vom Scheitelpunkt 0 zum Scheitelpunkt 3 oder von den Koordinaten [-1, 1, 1] zu den Koordinaten [1, 1, 1] gezogen werden. Wir müssen Informationen zu jeder Zeile im Code manuell schreiben und das Bild des Würfels betrachten, aber wie geht das richtig? Wenn wir 12 Zeilen haben und jede Zeile einen Anfang und ein Ende hat, d.h. 2 Punkte alsoUm einen Würfel zu zeichnen, brauchen wir 24 Punkte? Dies ist die richtige Antwort, aber schauen wir uns das Bild des Würfels noch einmal an und achten Sie darauf, dass jede Linie des Würfels gemeinsame Scheitelpunkte hat, z. B. am Scheitelpunkt 0 sind 3 Linien verbunden, und so mit jedem Scheitelpunkt. Wir können Speicherplatz sparen und nicht die Koordinaten von Anfang und Ende jeder Zeile aufschreiben. Erstellen Sie einfach ein Array und geben Sie die Scheitelpunktindizes aus dem Scheitelpunktarray an, in dem diese Zeilen beginnen und enden. Erstellen wir ein solches Array und beschreiben es nur mit Scheitelpunktindizes, 2 Indizes pro Zeile (Anfang der Zeile und Ende). Und ein wenig weiter, wenn wir diese Linien zeichnen, können wir ihre Koordinaten leicht aus dem Scheitelpunktarray erhalten. Mein Array von Linien (ich habe es Kanten genannt, weil dies die Kanten des Würfels sind) Ich habe unten ein Array von Eckpunkten erstellt und es sieht folgendermaßen aus:Aber schauen wir uns das Bild des Würfels noch einmal an und achten wir darauf, dass jede Linie des Würfels gemeinsame Scheitelpunkte hat, zum Beispiel am Scheitelpunkt 0 sind 3 Linien verbunden, und so mit jedem Scheitelpunkt. Wir können Speicherplatz sparen und nicht die Koordinaten von Anfang und Ende jeder Zeile aufschreiben. Erstellen Sie einfach ein Array und geben Sie die Scheitelpunktindizes aus dem Scheitelpunktarray an, in dem diese Zeilen beginnen und enden. Erstellen wir ein solches Array und beschreiben es nur mit Scheitelpunktindizes, 2 Indizes pro Zeile (Anfang der Zeile und Ende). Und ein wenig weiter, wenn wir diese Linien zeichnen, können wir ihre Koordinaten leicht aus dem Scheitelpunktarray erhalten. Mein Array von Linien (ich habe es Kanten genannt, weil dies die Kanten des Würfels sind) Ich habe unten ein Array von Eckpunkten erstellt und es sieht folgendermaßen aus:Aber schauen wir uns das Bild des Würfels noch einmal an und achten wir darauf, dass jede Linie des Würfels gemeinsame Scheitelpunkte hat, zum Beispiel am Scheitelpunkt 0 sind 3 Linien verbunden, und so mit jedem Scheitelpunkt. Wir können Speicherplatz sparen und nicht die Koordinaten von Anfang und Ende jeder Zeile aufschreiben. Erstellen Sie einfach ein Array und geben Sie die Scheitelpunktindizes aus dem Scheitelpunktarray an, in dem diese Zeilen beginnen und enden. Erstellen wir ein solches Array und beschreiben es nur mit Scheitelpunktindizes, 2 Indizes pro Zeile (Anfang der Zeile und Ende). Und ein wenig weiter, wenn wir diese Linien zeichnen, können wir ihre Koordinaten leicht aus dem Scheitelpunktarray erhalten. Mein Array von Linien (ich habe es Kanten genannt, weil dies die Kanten des Würfels sind) Ich habe unten ein Array von Eckpunkten erstellt und es sieht folgendermaßen aus:und so mit jedem Scheitelpunkt. Wir können Speicherplatz sparen und nicht die Koordinaten von Anfang und Ende jeder Zeile aufschreiben. Erstellen Sie einfach ein Array und geben Sie die Scheitelpunktindizes aus dem Scheitelpunktarray an, in dem diese Zeilen beginnen und enden. Erstellen wir ein solches Array und beschreiben es nur mit Scheitelpunktindizes, 2 Indizes pro Zeile (Anfang der Zeile und Ende). Und ein wenig weiter, wenn wir diese Linien zeichnen, können wir ihre Koordinaten leicht aus dem Scheitelpunktarray erhalten. Mein Array von Linien (ich habe es Kanten genannt, weil dies die Kanten des Würfels sind) Ich habe unten ein Array von Eckpunkten erstellt und es sieht folgendermaßen aus:und so mit jedem Scheitelpunkt. Wir können Speicherplatz sparen und nicht die Koordinaten von Anfang und Ende jeder Zeile aufschreiben. Erstellen Sie einfach ein Array und geben Sie die Scheitelpunktindizes aus dem Scheitelpunktarray an, in dem diese Zeilen beginnen und enden. Erstellen wir ein solches Array und beschreiben es nur mit Scheitelpunktindizes, 2 Indizes pro Zeile (Anfang der Zeile und Ende). Und ein wenig weiter, wenn wir diese Linien zeichnen, können wir ihre Koordinaten leicht aus dem Scheitelpunktarray erhalten. Mein Array von Linien (ich habe es Kanten genannt, weil dies die Kanten des Würfels sind) Ich habe unten ein Array von Eckpunkten erstellt und es sieht folgendermaßen aus:2 Indizes in jeder Zeile (der Anfang der Zeile und das Ende). Und ein wenig weiter, wenn wir diese Linien zeichnen, können wir ihre Koordinaten leicht aus dem Scheitelpunktarray erhalten. Mein Array von Linien (ich habe es Kanten genannt, weil dies die Kanten des Würfels sind) Ich habe unten ein Array von Eckpunkten erstellt und es sieht folgendermaßen aus:2 Indizes in jeder Zeile (der Anfang der Zeile und das Ende). Und ein wenig weiter, wenn wir diese Linien zeichnen, können wir ihre Koordinaten leicht aus dem Scheitelpunktarray erhalten. Mein Array von Linien (ich habe es Kanten genannt, weil dies die Kanten des Würfels sind) Ich habe unten ein Array von Eckpunkten erstellt und es sieht folgendermaßen aus:

// Cube edges
const edges = [
  [0, 1],
  [1, 2],
  [2, 3],
  [3, 0],

  [0, 4],
  [1, 5],
  [2, 6],
  [3, 7],

  [4, 5],
  [5, 6],
  [6, 7],
  [7, 4],
];

Dieses Array enthält 12 Indexpaare, 2 Scheitelpunktindizes pro Zeile.

Machen wir uns mit einer anderen Matrix vertraut, die unseren Würfel vergrößert, und versuchen wir schließlich, sie auf dem Bildschirm zu zeichnen. Die Skalenmatrix sieht folgendermaßen aus:

[\begin{matrix} s x & 0 & 0 & 0 \\ 0 & s y & 0 & 0 \\ 0 & 0 & s z & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$\begin{bmatrix}sx&0&0&0\\0&sy&0&0\\0&0&sz&0\\0&0&0&1\end{bmatrix}$

Die Parameter sx, sy, sz auf der Hauptdiagonale geben an, wie oft das Objekt vergrößert werden soll. Wenn wir 10, 10, 10 anstelle von sx, sy, sz in die Matrix einsetzen und diese Matrix mit den Eckpunkten des Würfels multiplizieren, wird unser Würfel zehnmal größer und nicht mehr 2 mal 2 mal 2, sondern 20 mal 20 mal größer 20. Sowohl

für die Skalierungsmatrix als auch für die Verschiebungsmatrix implementieren wir die Methode in der Matrix-Klasse, die die Matrix mit den bereits ersetzten Argumenten zurückgibt:

static getScale(sx, sy, sz) {
  return [
    [sx, 0, 0, 0],
    [0, sy, 0, 0],
    [0, 0, sz, 0],
    [0, 0, 0, 1],
  ]
}

Visualisierungsförderer

Wenn wir jetzt versuchen, einen Würfel mit Linien unter Verwendung der aktuellen Koordinaten der Scheitelpunkte zu zeichnen, erhalten wir einen sehr kleinen Zwei-Pixel-Würfel in der oberen linken Ecke des Bildschirms, weil Der Ursprung der Leinwand ist da. Lassen Sie uns alle Scheitelpunkte des Würfels durchlaufen und sie mit der Skalierungsmatrix multiplizieren, um den Würfel größer zu machen, und dann mit der Verschiebungsmatrix, um den Würfel nicht in der oberen linken Ecke, sondern in der Mitte des Bildschirms zu sehen. Ich habe den Code zum Auflisten von Scheitelpunkten mit Matrixmultiplikation unten Array von Kanten und sieht so aus:

const sceneVertices = []
for(let i = 0 ; i < vertices.length ; i++) {
  let vertex = Matrix.multiplyVector(
    Matrix.getScale(100, 100, 100),
    vertices[i]
  );

  vertex = Matrix.multiplyVector(
    Matrix.getTranslation(400, -300, 0),
    vertex
  );

  sceneVertices.push(vertex);
}

Bitte beachten Sie, dass wir die ursprünglichen Scheitelpunkte des Würfels nicht ändern, sondern das Ergebnis der Multiplikation im Array sceneVertices speichern, da wir möglicherweise mehrere Würfel unterschiedlicher Größe in unterschiedlichen Koordinaten zeichnen möchten. Wenn wir die Anfangskoordinaten ändern, können wir den nächsten Würfel nicht zeichnen, t .zu. Es gibt nichts zu beginnen, die Anfangskoordinaten werden durch den ersten Würfel verfälscht. Im obigen Code habe ich den ursprünglichen Würfel in alle Richtungen um das 100-fache erhöht, indem ich alle Scheitelpunkte mit der Skalierungsmatrix mit den Argumenten 100, 100, 100 multipliziert habe, und ich habe auch alle Scheitelpunkte des Würfels nach rechts und unten um 400 bzw. -300 Pixel verschoben, seit wir dies getan haben Die Leinwandgrößen aus dem vorherigen Artikel sind 800 x 600, es ist nur die Hälfte der Breite und Höhe des Zeichenbereichs, mit anderen Worten der Mitte.

Wir haben die Scheitelpunkte bisher fertiggestellt, aber wir müssen dies alles noch mit drawLine und dem Kantenarray zeichnen. Schreiben wir eine weitere Schleife unter die Scheitelpunktschleife, um über die Kanten zu iterieren und alle Linien darin zu zeichnen:

drawer.clearSurface()

for (let i = 0, l = edges.length ; i < l ; i++) {
  const e = edges[i]

  drawer.drawLine(
    sceneVertices[e[0]].x,
    sceneVertices[e[0]].y,
    sceneVertices[e[1]].x,
    sceneVertices[e[1]].y,
    0, 0, 255
  )
}

ctx.putImageData(imageData, 0, 0)

Denken Sie daran, dass wir im letzten Artikel mit dem Zeichnen beginnen, indem wir den Bildschirm aus dem vorherigen Status löschen, indem wir die clearSurface-Methode aufrufen. Dann iteriere ich über alle Flächen des Würfels und zeichne den Würfel mit blauen Linien (0, 0, 255). Ich nehme die Koordinaten der Linien aus dem Array sceneVertices, t .zu. Es gibt bereits skalierte und verschobene Scheitelpunkte im vorherigen Zyklus, aber die Indizes dieser Scheitelpunkte stimmen mit den Indizes der ursprünglichen Scheitelpunkte aus dem Scheitelpunktarray überein, weil Ich habe sie verarbeitet und in das Array sceneVertices eingefügt, ohne die Reihenfolge zu ändern.

Wenn wir den Code jetzt ausführen, wird nichts auf dem Bildschirm angezeigt. Dies liegt daran, dass in unserem Koordinatensystem Y nach oben und im Koordinatensystem die Leinwand nach unten schaut. Es stellt sich heraus, dass es unseren Würfel gibt, aber er befindet sich außerhalb des Bildschirms. Um dies zu beheben, müssen wir das Bild in Y (Spiegel) spiegeln, bevor wir ein Pixel in der Drawer-Klasse zeichnen. Bisher reicht diese Option für uns aus. Daher sieht der Code zum Zeichnen eines Pixels für mich folgendermaßen aus:

drawPixel(x, y, r, g, b) {
  const offset = (this.width * -y + x) * 4;

  if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
    this.surface[offset] = r;
    this.surface[offset + 1] = g;
    this.surface[offset + 2] = b;
    this.surface[offset + 3] = 255;
  }
}

Es ist zu sehen, dass in der Formel zum Erhalten des Versatzes Y jetzt ein Minuszeichen hat und die Achse jetzt in die Richtung schaut, die wir benötigen. Auch bei dieser Methode habe ich eine Prüfung hinzugefügt, um die Grenzen des Pixelarrays zu überschreiten. Einige andere Optimierungen wurden aufgrund der Kommentare zum vorherigen Artikel in der Schubladenklasse angezeigt. Daher poste ich die gesamte Schubladenklasse mit einigen Optimierungen, und Sie können die alte Schublade durch diese ersetzen:

Verbesserter Code für Schubladenklassen

class Drawer {
  surface = null;
  width = 0;
  height = 0;

  constructor(surface, width, height) {
    this.surface = surface;
    this.width = width;
    this.height = height;
  }

  drawPixel(x, y, r, g, b) {
    const offset = (this.width * -y + x) * 4;

    if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
      this.surface[offset] = r;
      this.surface[offset + 1] = g;
      this.surface[offset + 2] = b;
      this.surface[offset + 3] = 255;
    }
  }

  drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
    const round = Math.trunc;
    x1 = round(x1);
    y1 = round(y1);
    x2 = round(x2);
    y2 = round(y2);

    const c1 = y2 - y1;
    const c2 = x2 - x1;

    const length = Math.max(
      Math.abs(c1),
      Math.abs(c2)
    );

    const xStep = c2 / length;
    const yStep = c1 / length;

    for (let i = 0 ; i <= length ; i++) {
      this.drawPixel(
        Math.trunc(x1 + xStep * i),
        Math.trunc(y1 + yStep * i),
        r, g, b,
      );
    }
  }

  clearSurface() {
    const surfaceSize = this.width * this.height * 4;
    for (let i = 0; i < surfaceSize; i++) {
      this.surface[i] = 0;
    }
  }
}

const drawer = new Drawer(
  imageData.data,
  imageData.width,
  imageData.height
);

Wenn Sie den Code jetzt ausführen, wird das folgende Bild auf dem Bildschirm angezeigt:

Hier können Sie sehen, dass es in der Mitte ein Quadrat gibt, obwohl wir erwartet hatten, einen Würfel zu bekommen, was ist los? In der Tat - dies ist der Würfel, er steht einfach perfekt perfekt ausgerichtet mit einer der Flächen (Seite) zu uns, so dass wir den Rest nicht sehen. Außerdem sind wir mit Projektionen noch nicht vertraut, und daher wird die Rückseite des Würfels mit der Entfernung nicht kleiner, wie im wirklichen Leben. Um sicherzustellen, dass dies wirklich ein Würfel ist, drehen wir ihn ein wenig, damit er wie das Bild aussieht, das wir zuvor gesehen haben, als wir das Scheitelpunktarray erstellt haben. Um das 3D-Bild zu drehen, können Sie 3 spezielle Matrizen verwenden, weil Wir können uns um eine der Achsen X, Y oder Z drehen, was bedeutet, dass es für jede Achse eine eigene Rotationsmatrix gibt (es gibt andere Rotationsarten, aber dies ist das Thema der nächsten Artikel). So sehen diese Matrizen aus:

R_{x} (a) = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & c o s (a) & - s i n (a) & 0 \\ 0 & s i n (a) & c o s (a) & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$R_x(a)=\begin{bmatrix}1&0&0&0\\0&cos(a)&-sin(a)&0\\0&sin(a)&cos(a)&0\\0&0&0&1\end{bmatrix}$

Rotationsmatrix der X-Achse

R_{y} (a) [\begin{matrix} c o s (a) & 0 & s i n (a) & 0 \\ 0 & 1 & 0 & 0 \\ - s i n (a) & 0 & c o s (a) & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$R_y(a)\begin{bmatrix}cos(a)&0&sin(a)&0\\0&1&0&0\\-sin(a)&0&cos(a)&0\\0&0&0&1\end{bmatrix}$

Rotationsmatrix der Y-Achse

R_{z} (a) [\begin{matrix} c o s (a) & - s i n (a) & 0 & 0 \\ s i n (a) & c o s (a) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$R_z(a)\begin{bmatrix}cos(a)&-sin(a)&0&0\\sin(a)&cos(a)&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}$

Rotationsmatrix der Z-Achse

Wenn wir die Eckpunkte des Würfels mit einer dieser Matrizen multiplizieren, dreht sich der Würfel um den angegebenen Winkel (a) um die Achse, die Rotationsmatrix, um die wir uns entscheiden. Es gibt einige Funktionen, wenn Sie mehrere Achsen gleichzeitig drehen, und wir werden sie unten betrachten. Wie Sie dem Matrixbeispiel entnehmen können, verwenden sie zwei Funktionen sin und cos, und JavaScript verfügt bereits über eine Funktion zur Berechnung von Math.sin (a) und Math.cos (a). Sie arbeiten jedoch mit dem Winkelmaß im Bogenmaß, was möglicherweise nicht das bequemste ist wenn wir das Modell drehen wollen. Zum Beispiel ist es für mich viel bequemer, etwas um 90 Grad (Gradmaß) zu drehen, was im Bogenmaß bedeutetPi / 2(Es gibt auch einen ungefähren Pi-Wert in JS, dies ist die Konstante Math.PI). Fügen wir der Matrix-Klasse drei Methoden hinzu, um Rotationsmatrizen mit einem akzeptierten Rotationswinkel in Grad zu erhalten, die wir in Bogenmaß umwandeln, weil Sie werden benötigt, damit die sin / cos-Funktionen funktionieren:

static getRotationX(angle) {
  const rad = Math.PI / 180 * angle;

  return [
    [1, 0, 0, 0],
    [0, Math.cos(rad), -Math.sin(rad), 0],
    [0, Math.sin(rad), Math.cos(rad), 0],
    [0, 0, 0, 1],
  ];
}

static getRotationY(angle) {
  const rad = Math.PI / 180 * angle;

  return [
    [Math.cos(rad), 0, Math.sin(rad), 0],
    [0, 1, 0, 0],
    [-Math.sin(rad), 0, Math.cos(rad), 0],
    [0, 0, 0, 1],
  ];
}

static getRotationZ(angle) {
  const rad = Math.PI / 180 * angle;

  return [
    [Math.cos(rad), -Math.sin(rad), 0, 0],
    [Math.sin(rad), Math.cos(rad), 0, 0],
    [0, 0, 1, 0],
    [0, 0, 0, 1],
  ];
}

Alle drei Methoden beginnen mit der Umrechnung von Grad in Bogenmaß. Danach setzen wir den Drehwinkel im Bogenmaß in die Rotationsmatrix ein und übergeben die Winkel in die Funktionen sin und cos. Warum die Matrix so ist, können Sie in den thematischen Artikeln mit einer sehr detaillierten Erklärung mehr über den Hub lesen. Andernfalls können Sie diese Matrizen als für uns berechnete Formeln wahrnehmen und wir können sicher sein, dass sie funktionieren.

Oben im Code haben wir zwei Zyklen implementiert, der erste konvertiert Scheitelpunkte, der zweite zeichnet Linien durch Scheitelpunktindizes. Als Ergebnis erhalten wir ein Bild von den Scheitelpunkten auf dem Bildschirm und nennen diesen Codeabschnitt die Visualisierungspipeline. Der Förderer, weil wir den Peak nehmen und wiederum verschiedene Operationen damit ausführen, skalieren, verschieben, drehen, rendern, wie auf einem normalen industriellen Förderer. Fügen wir nun zum ersten Zyklus in der Visualisierungspipeline hinzu, zusätzlich zur Skalierung und Drehung um die Achsen. Zuerst drehe ich mich um X, dann um Y, vergrößere dann das Modell und verschiebe es (die letzten beiden Aktionen sind bereits vorhanden), sodass der gesamte Schleifencode folgendermaßen aussieht:

for(let i = 0 ; i < vertices.length ; i++) {
  let vertex = Matrix.multiplyVector(
    Matrix.getRotationX(20),
    vertices[i]
  );

  vertex = Matrix.multiplyVector(
    Matrix.getRotationY(20),
    vertex
  );

  vertex = Matrix.multiplyVector(
    Matrix.getScale(100, 100, 100),
    vertex
  );

  vertex = Matrix.multiplyVector(
    Matrix.getTranslation(400, -300, 0),
    vertex
  );

  sceneVertices.push(vertex);
}

In diesem Beispiel habe ich alle Scheitelpunkte um die X-Achse um 20 Grad und dann um Y um 20 Grad gedreht und hatte bereits 2 verbleibende Transformationen. Wenn Sie alles richtig gemacht haben, sollte Ihr Würfel jetzt dreidimensional aussehen:

Das Drehen um die Achsen hat eine Funktion: Wenn Sie beispielsweise den Würfel zuerst um die Y-Achse und dann um die X-Achse drehen, unterscheiden sich die Ergebnisse:


Drehen Sie 20 Grad um X und dann 20 Grad um Y.	Drehen Sie 20 Grad um Y und dann 20 Grad um X.

Es gibt andere Funktionen. Wenn Sie beispielsweise den Würfel um 90 Grad auf der X-Achse, dann um 90 Grad auf der Y-Achse und schließlich um 90 Grad um die Z-Achse drehen, wird die Drehung um X durch die letzte Drehung um Z abgebrochen, und Sie erhalten dasselbe Das Ergebnis ist, als hätten Sie die Figur gerade um 90 Grad um die Y-Achse gedreht. Um zu sehen, warum dies geschieht, nehmen Sie ein rechteckiges (oder kubisches) Objekt in Ihre Hände (z. B. zusammengesetzten Rubik-Würfel), merken Sie sich die Anfangsposition des Objekts und drehen Sie es zuerst um 90 Grad um das imaginäre X und dann um 90 Grad um Y und um 90 Grad um Z und merken Sie sich, zu welcher Seite es zu Ihnen geworden ist. Beginnen Sie dann an der Ausgangsposition, an die Sie sich zuvor erinnert haben, und machen Sie dasselbe. Entfernen Sie die Windungen von X und Z und drehen Sie sich nur um Y - Sie werden sehen, dass das Ergebnis das gleiche ist.Jetzt werden wir dieses Problem nicht lösen und auf seine Details eingehen. Diese Rotation ist derzeit für uns völlig zufriedenstellend. Wir werden dieses Problem jedoch im dritten Teil erwähnen (wenn Sie jetzt mehr verstehen möchten, suchen Sie nach Artikeln auf dem Hub mit der Abfrage "Scharnierschloss"). .

Lassen Sie uns nun unseren Code ein wenig optimieren. Es wurde oben erwähnt, dass Matrixtransformationen durch Multiplizieren von Transformationsmatrizen miteinander kombiniert werden können. Versuchen wir nicht, jeden Vektor zuerst mit der Rotationsmatrix um X, dann um Y, dann mit der Skalierung und am Ende der Bewegung zu multiplizieren. Zuerst multiplizieren wir vor der Schleife alle Matrizen, und in der Schleife multiplizieren wir jeden Scheitelpunkt mit nur einer resultierenden Matrix. Ich habe den Code kam so heraus:

let matrix = Matrix.getRotationX(20);

matrix = Matrix.multiply(
  Matrix.getRotationY(20),
  matrix
);

matrix = Matrix.multiply(
  Matrix.getScale(100, 100, 100),
  matrix,
);

matrix = Matrix.multiply(
  Matrix.getTranslation(400, -300, 0),
  matrix,
);

const sceneVertices = [];
for(let i = 0 ; i < vertices.length ; i++) {
  let vertex = Matrix.multiplyVector(
    matrix,
    vertices[i]
  );

  sceneVertices.push(vertex);
}

In diesem Beispiel wird die Kombination von Transformationen 1 Mal vor dem Zyklus durchgeführt, und daher haben wir nur 1 Matrixmultiplikation mit jedem Scheitelpunkt. Wenn Sie diesen Code ausführen, sollte das Würfelmuster gleich bleiben.

Fügen wir die einfachste Animation hinzu: Wir ändern den Drehwinkel um die Y-Achse im Intervall. Beispielsweise ändern wir den Drehwinkel um die Y-Achse alle 100 Millisekunden um 1 Grad. Fügen Sie dazu den Code der Visualisierungspipeline in die Funktion setInterval ein, die wir zuerst im ersten Artikel verwendet haben. Der Code der Animationspipeline sieht folgendermaßen aus:

let angle = 0
setInterval(() => {
  let matrix = Matrix.getRotationX(20)

  matrix = Matrix.multiply(
    Matrix.getRotationY(angle += 1),
    matrix
  )

  matrix = Matrix.multiply(
    Matrix.getScale(100, 100, 100),
    matrix,
  )

  matrix = Matrix.multiply(
    Matrix.getTranslation(400, -300, 0),
    matrix,
  )

  const sceneVertices = []
  for(let i = 0 ; i < vertices.length ; i++) {
    let vertex = Matrix.multiplyVector(
      matrix,
      vertices[i]
    )

    sceneVertices.push(vertex)
  }

  drawer.clearSurface()

  for (let i = 0, l = edges.length ; i < l ; i++) {
    const e = edges[i]

    drawer.drawLine(
      sceneVertices[e[0]].x,
      sceneVertices[e[0]].y,
      sceneVertices[e[1]].x,
      sceneVertices[e[1]].y,
      0, 0, 255
    )
  }

  ctx.putImageData(imageData, 0, 0)
}, 100)

Das Ergebnis sollte folgendermaßen aussehen:

Das Letzte, was wir in diesem Teil tun werden, ist, die Achsen des Koordinatensystems auf dem Bildschirm so anzuzeigen, dass es sichtbar ist, um das sich unser Würfel dreht. Wir zeichnen die Y-Achse von der Mitte nach oben, 200 Pixel lang, die X-Achse nach rechts, ebenfalls 200 Pixel lang, und die Z-Achse zeichnen 150 Pixel nach unten und links (diagonal), wie ganz am Anfang des Artikels in der Abbildung des rechtshändigen Koordinatensystems gezeigt . Beginnen wir mit dem einfachsten Teil, das sind die X-, Y-Achsen, weil ihre Linie verschiebt sich nur in eine Richtung. Fügen Sie nach der Schleife, die den Würfel zeichnet (Kantenschleife), das Rendering der X- und Y-Achse hinzu:

const center = new Vector(400, -300, 0)
drawer.drawLine(
  center.x, center.y,
  center.x, center.y + 200,
  150, 150, 150
)

drawer.drawLine(
  center.x, center.y,
  center.x + 200, center.y,
  150, 150, 150
)

Der mittlere Vektor ist die Mitte des Zeichenfensters, weil Wir haben die aktuellen Abmessungen von 800 mal 600 und -300 für Y, wie ich angegeben habe, weil Die drawPixel-Funktion dreht Y um und macht seine Richtung für die Leinwand geeignet (auf der Leinwand schaut Y nach unten). Dann zeichnen wir 2 Achsen mit drawLine, wobei wir zuerst Y 200 Pixel nach oben (Ende der Y-Achsenlinie) und dann X 200 Pixel nach rechts (Ende der X-Achsenlinie) verschieben. Ergebnis: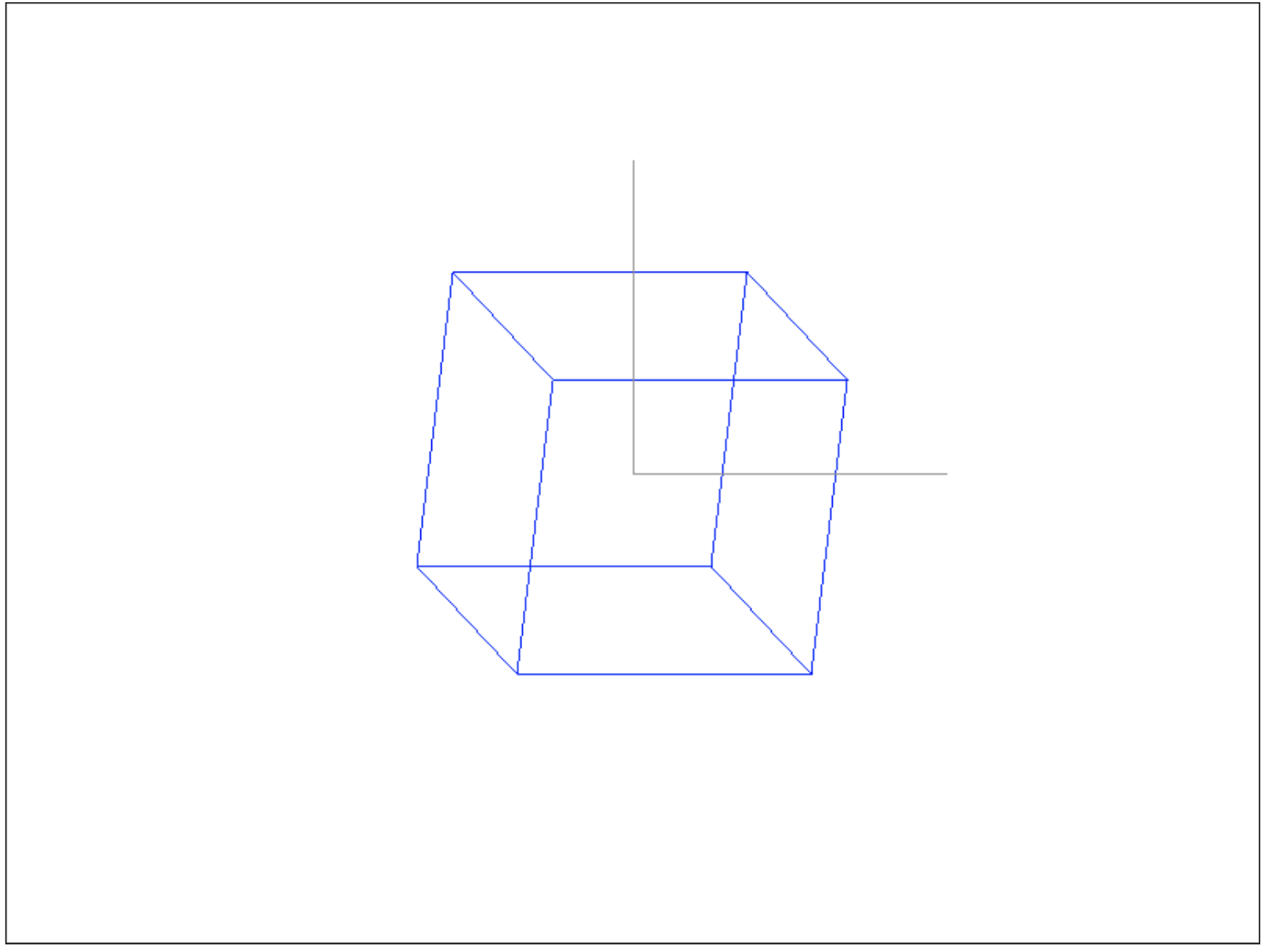

Zeichnen wir nun die Linie der Z-Achse, sie ist diagonal nach links unten und ihr Verschiebungsvektor ist [-1, -1, 0], und wir müssen auch eine Linie mit einer Länge von 150 Pixeln zeichnen, d. H. Der Versatzvektor [-1, -1, 0] sollte 150 lang sein, die erste Option ist [-150, -150, 0], aber wenn wir die Länge eines solchen Vektors berechnen, beträgt er ungefähr 212 Pixel. Zu Beginn dieses Artikels haben wir erläutert, wie Sie einen Vektor mit der gewünschten Länge korrekt erhalten. Zuerst müssen wir es normalisieren, um zu einer Länge von 1 zu führen, und dann die Länge, die wir erhalten möchten, mit dem Skalar multiplizieren, in unserem Fall 150. Und schließlich fassen wir die Koordinaten der Bildschirmmitte und den Verschiebungsvektor der Z-Achse zusammen, damit wir dahin gelangen Die Linie der Z-Achse sollte enden. Schreiben wir den Code nach dem Ausgabecode der beiden vorherigen Achsen, um die Linie der Z-Achse zu zeichnen:

const zVector = new Vector(-1, -1, 0);
const zCoords = Vector.add(
  center,
  zVector.normalize().multiplyByScalar(150)
);
drawer.drawLine(
  center.x, center.y,
  zCoords.x, zCoords.y,
  150, 150, 150
);

Als Ergebnis erhalten Sie alle 3 Achsen der gewünschten Länge:

In diesem Beispiel zeigt die Z-Achse nur, welches Koordinatensystem wir haben. Wir haben es diagonal gezeichnet, damit es sichtbar ist, weil Die reale Z-Achse steht senkrecht zu unserem Blick, und wir könnten sie mit einem Punkt auf dem Bildschirm zeichnen, der nicht schön wäre.

Insgesamt haben wir in diesem Artikel die Koordinatensysteme, Vektoren und mit einigen Operationen auf ihnen Matrizen und ihre Rollen bei Koordinatentransformationen verstanden, die Eckpunkte aussortiert und einen einfachen Förderer zur Visualisierung des Würfels und der Achsen des Koordinatensystems geschrieben, um die Theorie mit der Praxis zu fixieren. Der gesamte Anwendungscode ist unter dem Spoiler verfügbar:

Code für die gesamte Anwendung

const ctx = document.getElementById('surface').getContext('2d');
const imageData = ctx.createImageData(800, 600);

class Vector {
  x = 0;
  y = 0;
  z = 0;
  w = 1;

  constructor(x, y, z, w = 1) {
    this.x = x;
    this.y = y;
    this.z = z;
    this.w = w;
  }

  multiplyByScalar(s) {
    this.x *= s;
    this.y *= s;
    this.z *= s;

    return this;
  }

  static add(v1, v2) {
    return new Vector(
      v1.x + v2.x,
      v1.y + v2.y,
      v1.z + v2.z,
    );
  }

  getLength() {
    return Math.sqrt(
      this.x * this.x + this.y * this.y + this.z * this.z
    );
  }

  normalize() {
    const length = this.getLength();

    this.x /= length;
    this.y /= length;
    this.z /= length;

    return this;
  }
}

class Matrix {
  static multiply(a, b) {
    const m = [
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
      [0, 0, 0, 0],
    ];

    for (let i = 0 ; i < 4 ; i++) {
      for(let j = 0 ; j < 4 ; j++) {
        m[i][j] = a[i][0] * b[0][j] +
          a[i][1] * b[1][j] +
          a[i][2] * b[2][j] +
          a[i][3] * b[3][j];
      }
    }

    return m;
  }

  static getRotationX(angle) {
    const rad = Math.PI / 180 * angle;

    return [
      [1, 0, 0, 0],
      [0, Math.cos(rad), -Math.sin(rad), 0],
      [0, Math.sin(rad), Math.cos(rad), 0],
      [0, 0, 0, 1],
    ];
  }

  static getRotationY(angle) {
    const rad = Math.PI / 180 * angle;

    return [
      [Math.cos(rad), 0, Math.sin(rad), 0],
      [0, 1, 0, 0],
      [-Math.sin(rad), 0, Math.cos(rad), 0],
      [0, 0, 0, 1],
    ];
  }

  static getRotationZ(angle) {
    const rad = Math.PI / 180 * angle;

    return [
      [Math.cos(rad), -Math.sin(rad), 0, 0],
      [Math.sin(rad), Math.cos(rad), 0, 0],
      [0, 0, 1, 0],
      [0, 0, 0, 1],
    ];
  }

  static getTranslation(dx, dy, dz) {
    return [
      [1, 0, 0, dx],
      [0, 1, 0, dy],
      [0, 0, 1, dz],
      [0, 0, 0, 1],
    ];
  }

  static getScale(sx, sy, sz) {
    return [
      [sx, 0, 0, 0],
      [0, sy, 0, 0],
      [0, 0, sz, 0],
      [0, 0, 0, 1],
    ];
  }

  static multiplyVector(m, v) {
    return new Vector(
      m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
      m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
      m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
      m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
    );
  }
}

class Drawer {
  surface = null;
  width = 0;
  height = 0;

  constructor(surface, width, height) {
    this.surface = surface;
    this.width = width;
    this.height = height;
  }

  drawPixel(x, y, r, g, b) {
    const offset = (this.width * -y + x) * 4;

    if (x >= 0 && x < this.width && -y >= 0 && -y < this.height) {
      this.surface[offset] = r;
      this.surface[offset + 1] = g;
      this.surface[offset + 2] = b;
      this.surface[offset + 3] = 255;
    }
  }
  drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
    const round = Math.trunc;
    x1 = round(x1);
    y1 = round(y1);
    x2 = round(x2);
    y2 = round(y2);

    const c1 = y2 - y1;
    const c2 = x2 - x1;

    const length = Math.max(
      Math.abs(c1),
      Math.abs(c2)
    );

    const xStep = c2 / length;
    const yStep = c1 / length;

    for (let i = 0 ; i <= length ; i++) {
      this.drawPixel(
        Math.trunc(x1 + xStep * i),
        Math.trunc(y1 + yStep * i),
        r, g, b,
      );
    }
  }

  clearSurface() {
    const surfaceSize = this.width * this.height * 4;
    for (let i = 0; i < surfaceSize; i++) {
      this.surface[i] = 0;
    }
  }
}

const drawer = new Drawer(
  imageData.data,
  imageData.width,
  imageData.height
);

// Cube vertices
const vertices = [
  new Vector(-1, 1, 1), // 0 
  new Vector(-1, 1, -1), // 1 
  new Vector(1, 1, -1), // 2 
  new Vector(1, 1, 1), // 3 
  new Vector(-1, -1, 1), // 4 
  new Vector(-1, -1, -1), // 5 
  new Vector(1, -1, -1), // 6 
  new Vector(1, -1, 1), // 7 
];

// Cube edges
const edges = [
  [0, 1],
  [1, 2],
  [2, 3],
  [3, 0],

  [0, 4],
  [1, 5],
  [2, 6],
  [3, 7],

  [4, 5],
  [5, 6],
  [6, 7],
  [7, 4],
];

let angle = 0;
setInterval(() => {
  let matrix = Matrix.getRotationX(20);

  matrix = Matrix.multiply(
    Matrix.getRotationY(angle += 1),
    matrix
  );

  matrix = Matrix.multiply(
    Matrix.getScale(100, 100, 100),
    matrix,
  );

  matrix = Matrix.multiply(
    Matrix.getTranslation(400, -300, 0),
    matrix,
  );

  const sceneVertices = [];
  for(let i = 0 ; i < vertices.length ; i++) {
    let vertex = Matrix.multiplyVector(
      matrix,
      vertices[i]
    );

    sceneVertices.push(vertex);
  }

  drawer.clearSurface();

  for (let i = 0, l = edges.length ; i < l ; i++) {
    const e = edges[i];

    drawer.drawLine(
      sceneVertices[e[0]].x,
      sceneVertices[e[0]].y,
      sceneVertices[e[1]].x,
      sceneVertices[e[1]].y,
      0, 0, 255
    );
  }

  const center = new Vector(400, -300, 0)
  drawer.drawLine(
    center.x, center.y,
    center.x, center.y + 200,
    150, 150, 150
  );

  drawer.drawLine(
    center.x, center.y,
    center.x + 200, center.y,
    150, 150, 150
  );

  const zVector = new Vector(-1, -1, 0, 0);
  const zCoords = Vector.add(
    center,
    zVector.normalize().multiplyByScalar(150)
  );
  drawer.drawLine(
    center.x, center.y,
    zCoords.x, zCoords.y,
    150, 150, 150
  );

  ctx.putImageData(imageData, 0, 0);
}, 100);

Was weiter?

Im nächsten Teil werden wir uns überlegen, wie man die Kamera steuert und wie man eine Projektion erstellt (je weiter das Objekt entfernt ist, desto kleiner ist es), die Dreiecke kennenlernt und herausfindet, wie man daraus 3D-Modelle erstellt, analysiert, was Normalen sind und warum sie benötigt werden.